Aplicaciones de la fuerza de Lorentz

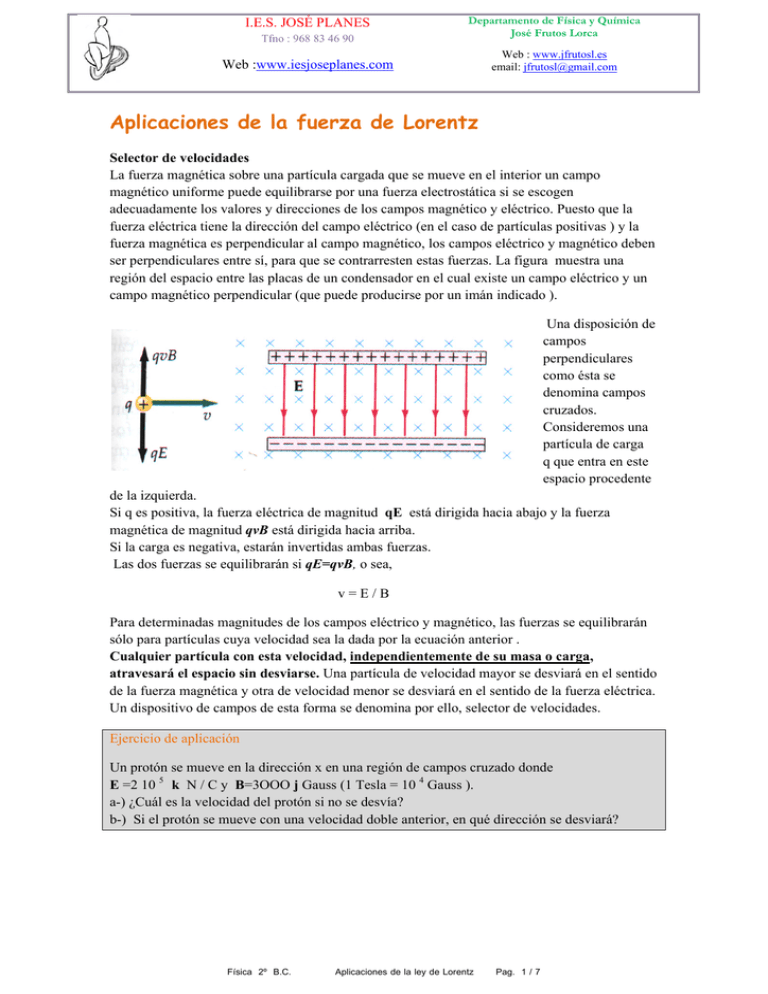
Tfno : 968 83 46 90
Departamento de Física y Química
José Frutos Lorca
Web :www.iesjoseplanes.com
Web : www.jfrutosl.es
email: jfrutosl@gmail.com
I.E.S. JOSÉ PLANES
Aplicaciones de la fuerza de Lorentz
Selector de velocidades
La fuerza magnética sobre una partícula cargada que se mueve en el interior un campo
magnético uniforme puede equilibrarse por una fuerza electrostática si se escogen
adecuadamente los valores y direcciones de los campos magnético y eléctrico. Puesto que la
fuerza eléctrica tiene la dirección del campo eléctrico (en el caso de partículas positivas ) y la
fuerza magnética es perpendicular al campo magnético, los campos eléctrico y magnético deben
ser perpendiculares entre sí, para que se contrarresten estas fuerzas. La figura muestra una
región del espacio entre las placas de un condensador en el cual existe un campo eléctrico y un
campo magnético perpendicular (que puede producirse por un imán indicado ).
Una disposición de
campos
perpendiculares
como ésta se
denomina campos
cruzados.
Consideremos una
partícula de carga
q que entra en este
espacio procedente
de la izquierda.
Si q es positiva, la fuerza eléctrica de magnitud qE está dirigida hacia abajo y la fuerza
magnética de magnitud qvB está dirigida hacia arriba.
Si la carga es negativa, estarán invertidas ambas fuerzas.
Las dos fuerzas se equilibrarán si qE=qvB, o sea,
v=E/B
Para determinadas magnitudes de los campos eléctrico y magnético, las fuerzas se equilibrarán
sólo para partículas cuya velocidad sea la dada por la ecuación anterior .
Cualquier partícula con esta velocidad, independientemente de su masa o carga,
atravesará el espacio sin desviarse. Una partícula de velocidad mayor se desviará en el sentido
de la fuerza magnética y otra de velocidad menor se desviará en el sentido de la fuerza eléctrica.
Un dispositivo de campos de esta forma se denomina por ello, selector de velocidades.
Ejercicio de aplicación
Un protón se mueve en la dirección x en una región de campos cruzado donde
E =2 10 5 k N / C y B=3OOO j Gauss (1 Tesla = 10 4 Gauss ).
a-) ¿Cuál es la velocidad del protón si no se desvía?
b-) Si el protón se mueve con una velocidad doble anterior, en qué dirección se desviará?
Física 2º B.C.
Aplicaciones de la ley de Lorentz
Pag. 1 / 7
Tfno : 968 83 46 90
Departamento de Física y Química
José Frutos Lorca
Web :www.iesjoseplanes.com
Web : www.jfrutosl.es
email: jfrutosl@gmail.com
I.E.S. JOSÉ PLANES
Medida de Thomson del cociente q/m para electrones
Un ejemplo del uso de un selector de velocidades es el famoso experimento de J.J. Thomson
en 1897, en el cual demostró que los rayos de los tubos de rayos catódicos podían desviarse
mediante campos eléctrico y magnético y, por consiguiente, se componían de partículas
cargadas. Observando la desviación de rayos con diversas combinaciones de campos eléctrico y
magnético, Thomson pudo demostrar que todas las partículas tenían la misma relación carga
masa q / m y determinar este cociente. Demostró que las partículas con esta razón carga a masa
pueden obtenerse utilizando un material cualquiera como cátodo que significa que estas
partículas, ahora denominadas electrones, son un constituyente fundamental de toda materia.
La figura muestra un diagrama
esquemático del tubo de rayos
catódicos utilizado por Thomson.
Los electrones son emitidos por el
cátodo C, que esta a un potencial
negativo respecto a las rendijas
A y B.
Existe un campo eléctrico en la
dirección que va desde A hasta C que acelera a los electrones. Estos pasan a través de las
rendijas A y B hacia el interior de una región libre de campo .Luego se encuentran con un
campo eléctrico entra las placas D y F que es perpendicular a la velocidad de los electrones. La
aceleración producida por este campo eléctrico da a los electrones un componente vertical de la
velocidad al abandonar la región situada entre las placas. A continuación inciden en la pantalla
fosforescente situada en el extremo del tubo en un punto que presenta un determinado
desplazamiento Δy respecto al punto en el cual incidirían si no existiese campo entre las placas
D y F. Cuando los electrones chocan contra la pantalla , produce un destello que indica la
posición del haz. La desviación Δy se produce en dos partes: Δ y 1 que tiene lugar mientras los
electrones se encuentran entre las placas, y Δ y 2 que tiene lugar una vez los electrones
abandonan la región entre las placas .
Sea x 1 la distancia horizontal a través de las placas deflectoras D y F.
Si los electrones se mueven horizontalmente con velocidad v 0 x al entrar en la región de las
placas, el tiempo que transcurre en esta región es t1 = x 1 / v 0 x y la velocidad vertical cuando
abandonan las placas es
v y = = a . t 1 = ( q E / m ). t 1 = q E / m . x 1 / v 0
Física 2º B.C.
Aplicaciones de la ley de Lorentz
Pag. 2 / 7
Tfno : 968 83 46 90
Departamento de Física y Química
José Frutos Lorca
Web :www.iesjoseplanes.com
Web : www.jfrutosl.es
email: jfrutosl@gmail.com
I.E.S. JOSÉ PLANES
siendo E el campo eléctrico existente entre las placas.
La desviación en esta región será
Δ y 1 = ½ 1 t 1 2 = ½ q E / m ( x1 / v 0 ) 2
El electrón entonces se mueve recorriendo una distancia horizontal adicional x 2 en la región
libre de campo entre las placas de deflexión y la pantalla.
Como la velocidad del electrón es constante en esta región, el tiempo necesario para alcanzar la
pantalla es t2=x 2 / v0 y la desviación vertical adicional es
Δ y 2 = vy t 2 = q E / m . x 1 / v 0 . x2 / v0
La desviación total en la pantalla es, por tanto,
Δ y = Δ y 1 + Δ y 2 = 1/ 2 q E / m ( x 1 / v0 ) 2 + q E / m . x1 x 2 / v 0 2
La velocidad inicial v0 se determina introduciendo un campo magnético B entre las placas en
una dirección perpendicular tanto al campo eléctrico como a la velocidad inicial de los
electrones.
La magnitud de B se ajusta entonces hasta que el haz no se desvía , y la velocidad se determina
mediante la ecuación del selector de velocidades . La desviación medida Δ y se utiliza para
determinar la relación carga-masa, q/m según la ecuación anterior.
Ejemplo de calculo
Los electrones pasan sin desviarse a través de las placas del aparato de Thomson cuando el
campo eléctrico es de 3000 V/m y existe un campo magnético cruzado de 1,40 G.
Sí las placas tienen 4 cm de longitud y el extremo de las placas dista 30 cm de la pantalla,
determinar la desviación sobre la pantalla cuando se interrumpe el campo magnético.
En este ejemplo utilizamos la carga e = 1,6 . 10 - 19 C y la masa m=9,11. 10 - 31 kg conocidas del
electrón para determinar la desviación Δy. La velocidad inicial de los electrones se determina a
partir de la ecuación
v 0 = E / B = 3000 / 1,4 . 10
-4
= 2,14 . 10 7 m / s
Utilizando la ecuación de la desviación con v 0= 2,14 .10 7 m/s, x1 =4 cm y x2=30 cm se obtiene
para la desviación Δ y = 9,2 . 10 - 4 m + 1,38 . 10 - 2 m = 14 , 7 mm
Física 2º B.C.
Aplicaciones de la ley de Lorentz
Pag. 3 / 7
Tfno : 968 83 46 90
Departamento de Física y Química
José Frutos Lorca
Web :www.iesjoseplanes.com
Web : www.jfrutosl.es
email: jfrutosl@gmail.com
I.E.S. JOSÉ PLANES
Espectrómetro de masas
El espectrómetro de masas, diseñado
por vez primera por Francis William
Aston en 1919 y mejorado
posteriormente por Kenneth
Bainbridge y otros, fue desarrollado
para medir las masas de los isótopos.
Estas medidas constituyen un medio
importante para la determinación de la
existencia de isótopos y su abundancia
en la naturaleza. Por ejemplo, así se
comprobó que el magnesio natural está
formado por 78,7 por ciento de 24Mg,
10,1 por ciento de 25Mg y 11,2 por
ciento 26Mg.
Estos isótopos poseen masas en la
relación aproximada 24:25:26.
El espectrómetro de masas se utiliza para determinar la relación masa-carga de iones de carga
conocida midiendo el radio de sus órbitas circulares en un campo magnético conocido. La
ecuación r= m v / qB nos ofrece el radio r par la órbita circular de una partícula de masa m y
carga q que se mueve con velocidad v en un campo magnético B perpendicular a la velocidad de
la partícula. la figura 24-16 muestra un dibujo esquemático simple de un espectrómetro de
masas.
Los iones procedentes de una fuente, son acelerados por un campo eléctrico y entran en un
campo magnético uniforme producido por un electroimán.
Si los iones parten del reposo y se mueven a través de una diferencia de potencial ΔV, su
energía cinética cuando entren en el imán es igual a la pérdida de energía potencial, q Δ V:
½mv2 =qΔV
Los iones se mueven en una semicircunferencia de radio r dado por la ecuación anterior e
inciden sobre una película fotográfica P 2 a una distancia 2r del punto en el que entraron en el
electroimán. La velocidad v puede eliminarse entre las ecuaciones
de
r=mv/qB
Æ
v=rqB/m Æ
v2 =(rqB/m)2
por tanto ½ m ( r q B / m ) 2 = q Δ V simplificando esta ecuación y despejando m / q
m/q =B2r2/2.ΔV
En el espectrómetro de masas original de Aston, las diferencias de masas podían medirse con
una precisión de 1 parte en 10 000. La precisión se ha mejorado por la introducción de un
selector de velocidades entre la fuente de iones y el imán, haciendo posible determinar la
velocidad de los iones exactamente y limitar el margen de velocidades de los iones que entran
en la zona del imán.
Física 2º B.C.
Aplicaciones de la ley de Lorentz
Pag. 4 / 7
Tfno : 968 83 46 90
Departamento de Física y Química
José Frutos Lorca
Web :www.iesjoseplanes.com
Web : www.jfrutosl.es
email: jfrutosl@gmail.com
I.E.S. JOSÉ PLANES
Ejemplo de calculo
Un ion de 58Ni de carga + e y masa 9,62 . 10 - 26 Kg se acelera a través de una diferencia de
potencial de 3 kV y se desvía en un campo magnético de 0,12 T.
a - ) Determinar el radio de curvatura de la órbita del ion.
b - ) Determinar la diferencia que existe entre los radios de curvatura de los iones 58Ni y 60Ni.
De la ecuación ultima se obtiene r 2 = 2 . m Δ V / q B 2 = 0,251 Æ r = 0,501 m
b-) El radio de la órbita de un ion en un determinado campo magnético es proporcional a la raíz
cuadrada de su masa para un determinado voltaje acelerador.
Si r1, es el radio de la órbita del ion 58Ni y r2 el de la órbita del ion 60Ni, la relación de los radios
es r 2 / r 1 = ( m 2 / m 1 ) 1/2
Por tanto, el radio de la órbita del ion 60Ni es
r2 = ( 60 / 58 ) 1/2 = 0,510 m
La diferencia entre los radios de las órbitas es
r2 - r1 = 0,510 m - 0,501 m = 0,009 m = 9 mm
El ciclotrón
El ciclotrón fue inventado
por E. O. Lawrence y M. 5.
Livingston en 1932 para
acelerar partículas tales como
protones o deuterones hasta
conseguir una energía
cinética elevada.
(El deuterón es el núcleo de
hidrógeno pesado, 2H,
formado por un protón y un
neutrón fuertemente ligados
entre si ) Las partículas de
energía alta se utilizan a
continuación para
bombardear los núcleos,
produciendo reacciones
nucleares que se estudian con
objeto de obtener
información acerca del núcleo. Se utilizan también protones o deuterones de alta energía para
producir materiales radiactivos y con fines médicos. El funcionamiento del ciclotrón se basa en
el hecho de que el período de movimiento de una partícula cargada en el interior de un campo
Física 2º B.C.
Aplicaciones de la ley de Lorentz
Pag. 5 / 7
Tfno : 968 83 46 90
Departamento de Física y Química
José Frutos Lorca
Web :www.iesjoseplanes.com
Web : www.jfrutosl.es
email: jfrutosl@gmail.com
I.E.S. JOSÉ PLANES
magnético uniforme es independiente de la velocidad de la partícula, como indica la ecuación
T=2.πm/qB
L a figura es un dibujo esquemático de un ciclotrón. Las partículas se mueven en el interior de
dos recipientes metálicos semicirculares denominados des (debido a su forma ). Los recipientes
están contenidos en una cámara de vacío en el interior de un campo magnético proporcionado
por un electroimán. (En la región en la cual se mueven las partículas debe haberse realizado el
vacío para que las partículas no pierdan energía y no sean dispersadas en choques con las
moléculas del aire.)
Las des se mantienen a una diferencia de potencial ΔV que se alterna en el tiempo con período
T, escogido de modo que sea igual al período del ciclotrón dado por la ecuación anterior.
Esta diferencia de potencial crea un campo eléctrico con el espacio hueco comprendido entre
las dos. Al mismo tiempo no existe campo eléctrico dentro de las des debido al blindaje
metálico.Las partículas cargadas se inyectan inicialmente en la de 1 con una velocidad pequeña
procedentes de una fuente de iones S próxima al centro de las des. Se mueven en una
semicircunferencia en una de las des y llegan al espacio situado entre las des al cabo de un
tiempo ½ T, en donde T es el período del ciclotrón y también el período del potencial alterno
aplicado a las des.
La alternancia del potencial se ajusta de modo que la de 1 está a mayor potencial que la de 2
cuando las partículas llegan al espacio hueco entre ambas. Cada partícula se acelera, por tanto, a
través de este hueco a causa del campo eléctrico y gana una energía cinética igual a q ΔV. Al
poseer más energía cinética, la partícula se mueve en un semicírculo de mayor radio en la de 2 y
de nuevo llega al hueco después de un tiempo ½ T. En este tiempo el potencial entre las des se
ha invertido de modo que la de 2 está ahora a mayor potencial. De nuevo la partícula se acelera
a través del hueco y gana energía cinética adicional igual a q Δ V.
Cada vez que la partícula llega al hueco, es acelerada y gana energía cinética igual a q ΔV.
De este modo se mueve en órbitas semicirculares cada vez mayores hasta que eventualmente
abandona el campo magnético. En un ciclotrón típico, cada partícula realiza de 50 a 100
revoluciones y emerge con energías de hasta varios centenares de Mega electrón Voltio.
Esta energía cinética de una partícula que emerge de un ciclotrón puede calcularse mediante la
ecuación del radio de una órbita circular descrita por una partícula en el seno de un campo
magnético constante
r = m v / q B sustituyendo r por el valor máximo del radio de las des y despejando el valor de v:
Si r max = m v / q B
Æ v = q B r max / m por tanto
E cinetica = ½ m v 2 = ½ ( q2 B 2 / m ) r max 2
Física 2º B.C.
Aplicaciones de la ley de Lorentz
Pag. 6 / 7
Tfno : 968 83 46 90
Departamento de Física y Química
José Frutos Lorca
Web :www.iesjoseplanes.com
Web : www.jfrutosl.es
email: jfrutosl@gmail.com
I.E.S. JOSÉ PLANES
Ejemplo de calculo
Un ciclotrón que acelera protones posee un campo magnético de 1,5 T y un radio máximo de
0,5 m.
a -) ¿Cuál es la frecuencia del ciclotrón?
b- ) Determinar la energía cinética con que emergen los protones.
(a) El periodo de una partícula en un campo magnético constante viene dado por
T = 2 . π m / q B por tanto la frecuencia del ciclotrón viene dada por la ecuación
f=qB/2πm
= ( sustituyendo directamente ) = 22,9 Hz
b-)La energía cinética de los protones emergentes viene dada por la ecuación
E cinetica = ½ m v 2 = ½ ( q2 B 2 / m ) r max 2
E cinetica = 4,31 . 10
- 12
Julios
Las energías de los protones y otras partículas elementales se expresan usualmente en electrónvoltios. Como 1 eV = 1,6 . 10 - 19 Julios , resulta E cinetica = 26 , 9 MeV ( Millones de electrón
voltios)
Física 2º B.C.
Aplicaciones de la ley de Lorentz
Pag. 7 / 7