S - Canek
Anuncio

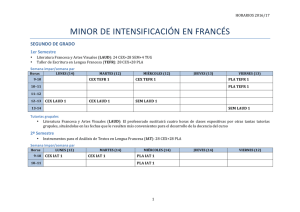
1 Soluciones de ecuaciones diferenciales. E: Verificar que la función es solución de la ecuación diferencial dada. En cualquier caso, las C (con subíndice o sin él) que aparezcan son constantes. y 0 D e .x y/ I y D ln.C C e x /. S: Se deriva y: y D ln.C C e x / ) y 0 D ex : C C ex Se sustituye y 0 & y en la ED: ex D e Œx x C Ce ln.C Cex / ex ) D ex e x C Ce ln.C Cex / ex ex ) D ln.C Cex / ) C C ex e ex ex D C C ex C C ex Esta última igualdad permite concluir que la función es solución de la ecuación diferencial. ) 10. canek.azc.uam.mx: 26/ 10/ 2010