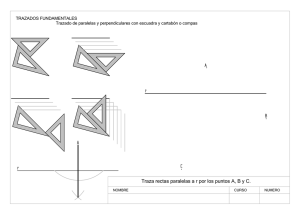
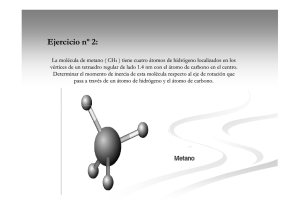
tp 4. Composición y descomposición de fuerzas
Anuncio

1 INTRODUCCIÓN A LOS TIPOS ESTRUCTURALES Cat. Ing. CANCIANI TRABAJO PRÁCTICO Nº 4: COMPOSICIÓN DE FUERZAS 4.1- Componer el siguiente sistema de Fuerzas Concurrentes gráficamente. Hallar la Fuerza Resultante y la Equilibrante. Grupo 1 – 11 2 – 12 3 – 13 4 – 14 5 – 15 6 – 16 7 – 17 8 – 18 9 – 19 10 - 20 4.2- F1 5t 4t 5t 4t 6t 5t 4t 5t 6t 8t F2 8t 6t 4t 10 t 8t 8t 10 t 10 t 8t 10 t F3 6t 8t 6t 8t 4t 6t 8t 6t 10 t 6t ά β γ 30º 20º 20º 30º 30º 20º 30º 20º 30º 20º 60º 45º 60º 60º 45º 60º 60º 60º 45º 30º 60º 30º 60º 30º 30º 60º 30º 60º 30º 30º Descomponer la fuerza F en las direcciones 1 y 2 gráficamente. Grupo 1 – 11 2 – 12 3 – 13 4 – 14 5 – 15 6 – 16 7 – 17 8 – 18 9 – 19 10 - 20 F 5t 4t 5t 4t 6t 5t 4t 5t 6t 8t ά β γ 30º 20º 20º 30º 30º 20º 30º 20º 30º 20º 60º 45º 60º 60º 45º 60º 60º 60º 45º 30º 60º 30º 60º 30º 30º 60º 30º 60º 30º 30º 2 4.3- Componer el siguiente Sistema de Fuerzas no concurrente. Hallar la Fuerza Resultante y la Equilibrante. Grupo 1 – 11 2 – 12 3 – 13 4 – 14 5 – 15 6 – 16 7 – 17 8 – 18 9 – 19 10 - 20 4.4- F1 10 t 12 t 15 t 20 t 10 t 15 t 20 t 10 t 10 t 15 t F2 8t 6t 4t 10 t 8t 8t 10 t 10 t 8t 10 t F3 6t 8t 6t 8t 4t 6t 8t 6t 10 t 6t ά β γ 30º 20º 20º 30º 30º 20º 30º 20º 30º 20º 60º 45º 60º 60º 45º 60º 60º 60º 45º 30º 60º 30º 60º 30º 30º 60º 30º 60º 30º 30º Componer la Fuerza y el Par. Grupo 1 – 11 2 – 12 3 – 13 4 – 14 5 – 15 6 – 16 7 – 17 8 – 18 9 – 19 10 - 20 F 5t 4t 5t 4t 6t 8t 4t 10 t 6t 8t M 30 tm 20 tm 20 tm 20 tm 30 tm 24 tm 40 tm 20 tm 30 tm 40 tm 3 RESOLUCIÓN DE EJERCICIOS 4.1a) Construcción del Sistema de Fuerzas concurrentes, determinando para ello una escala gráfica. DATOS F1 F2 4t 8t F3 8t ά β γ 30º 60º 45º b) Construcción del Polígono de Fuerzas. Como gráfico auxiliar, se dibujan las fuerzas una a continuación de la otra, con igual sentido, dirección e intensidad que en el sistema. El orden en el cual se colocan las fuerzas es aleatorio. c) Obtención de la Fuerza Resultante. La Resultante surge de unir el origen de la primera fuerza que dibujamos con el extremo de la última. A través de la escala gráfica se determina la intensidad de R y su dirección, a través del ángulo entre la recta de acción y el eje x. 4 d) Se transporta paralelamente desde el polígono al sistema inicial, haciéndola pasar por el punto de concurrencia O. e) Determinación de la Fuerza Equilibrante. La Equilibrante surge de unir el extremo de la última fuerza con el origen de primera, obteniendo de esta manera un polígono CERRADO. E es una fuerza de igual recta de acción, intensidad y sentido contrario que el de la resultante R. 5 4.2a) Planteo gráfico: fuerza F a descomponer cuya recta de acción se corta con otras dos rectas, d1 y d2, en un punto O. DATOS F ά β γ 6 t 20º 60º 45º b) Construcción de un triángulo de fuerzas ABC. En un gráfico auxiliar se dibuja la fuerza F. Por los extremos de ésta, A y C, se trazan sendas paralelas a las rectas d1 y d2 que se cortan en el punto B. c) Obtención de las fuerzas F1 y F2. Los segmentos definidos por la intersección de las tres rectas de acción determinan las magnitudes de F1 y de F2. El sentido de las mismas será tal que el recorrido F1-F2 llegará al mismo punto que recorriendo F. 6 4.3a) Construcción del Sistema de Fuerzas, determinando para ello una escala gráfica. DATOS F1 F2 4t 8t F3 8t ά β γ 30º 60º 45º b) Construcción del Polígono de Fuerzas. Como gráfico auxiliar, se dibujan las fuerzas una a continuación de la otra, con igual sentido, dirección e intensidad que en el sistema. El orden en el cual se colocan las fuerzas es aleatorio. c) Obtención de la Fuerza Resultante. La Resultante surge de unir el origen de la primera fuerza que dibujamos con el extremo de la última. A través de la escala gráfica se determina la intensidad de R y su dirección, a través del ángulo entre la recta de acción y el eje x. 7 d) Construcción del Polígono Funicular. Se toma un punto cualquiera O, llamado Polo y se trazan los Rayos Polares que unen el polo con los puntos A, B, C y D del polígono de fuerzas. Se numeran los rayos polares correlativamente: 1, 2, 3 y 4. e) Ubicación de la resultante en el sistema. Se trasladan paralelamente los Rayos Polares uno a uno al Sistema de Fuerzas. En la intersección del primero y el último, se determina un punto de la recta de acción de la resultante R. Sobre dicho punto, se traslada la resultante R del polígono de fuerzas. 8 4.4Componer una fuerza y un par significa hallar la resultante del sistema por ellos formados. Supongamos una fuerza F y un par de momento M. DATOS F M 6t - 30 tm a) Construcción del Sistema de Fuerzas. Como el par tiene infinitas imágenes, elegimos la que más convenga. Ella es tal que, una de las componentes del par sea una fuerza de igual intensidad, la misma recta de acción y sentido contrario al de la fuerza F dada. La otra componente del par valdrá también F y estará separada de la anterior por una distancia d. Dado que el valor del par es M = P.d d= M P Ha quedado formada una bifuerza que se puede suprimir y queda una sola fuerza F de intensidad igual a la dada, paralela a ella y separada por una distancia que resulta de dividir el valor del par por el valor de la fuerza. CONCLUSIÓN: componer una fuerza con un par da por resultado una fuerza de igual intensidad, dirección y sentido que la fuerza dada, pero trasladada paralelamente a sí misma, una distancia que surge de dividir el valor del par por el de la fuerza.