tecnología electrónica tema 4(circuitos con diodos)

TECNOLOGÍA ELECTRÓNICA
TEMA 4 (CIRCUITOS CON DIODOS)
EJEMPLOS RESUELTOS
JULIO BRÉGAINS, DANIEL IGLESIA, JOSÉ LAMAS
DEPARTAMENTO DE ELECTRÓNICA E SISTEMAS
FACULTADE DE INFORMÁTICA,
UNIVERSIDADE DA CORUÑA
Aprendí muy pronto la diferencia entre
saber el nombre de algo, y saber algo (Richard P. Feynman).
EJEMPLO 1 (T4):
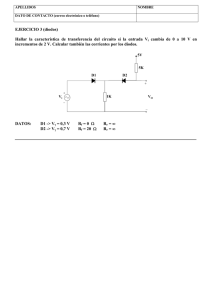
Suponiendo diodos ideales, determinar y representar la función de transferencia Io = f(Vi),
indicando en cada zona el estado de los diodos, con R = 750 [W], VR1 = VR2 = 1[V], RL = 250 [W].
FIGURA T4. 1
PLANTEAMIENTO Y RESOLUCIÓN
¿CÓMO SE OBTIENE LA CORRIENTE IO QUE CIRCULA SOBRE RL EN FUNCIÓN DE LA TENSIÓN DE ENTRADA Vi?
Hacemos variar Vi desde valores negativos muy grandes hasta valores positivos muy grandes, y
analizamos por tramos (zonas). Para ello, antes es necesario tener claro que Vi positiva significa
que el potencial en el punto a es mayor que en el punto f, es decir:
Vi > 0 Þ Va > Vf
Y de modo análogo,
Vi < 0 Þ Va < Vf
PRIMER TRAMO: Supongamos Vi << 0 (i.e., Vi negativa, mucho menor que cero). Por tanto, Va << Vf, de
donde se deduce que el potencial en el punto e será mayor que en el punto b (la tensión VR1 no tiene
mayor influencia, ya que es sólo de 1 V, muy pequeña, en valor absoluto, comparada con Vi).
Entonces, como Ve > Vb Þ VA1 > VK1 (con VR1 pequeña) Þ D1 conduce (D1 ON).
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 2 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
Los puntos e y d están al mismo potencial (no hay resistencia entre ellos) y lo mismo sucede con los
puntos b y c. De este modo Ve = Vd y Vb = Vc.
Entonces, también Vd > Vc Þ VA2 < VK2 (VR2 pequeña) Þ D2 está abierto (D2 OFF)I.
El circuito equivalente es, consecuentemente:
En este estado, la fuente de tensión VR2 no tiene efecto, por estar en circuito abierto, sobre la
corriente Io. La fuente VR1, en cambio, fija la tensión entre los puntos e y b (Ve>Vb), que será la tensión
en los extremos de la resistencia. Aplicando ley de Ohm sobre RL podemos obtener el valor de Io:
Io =
Ve - Vb Vd - Vc VR1
1[V]
4
=
=
=
= 0,004 [A] =
[A] Þ Io = 4[mA]
RL
RL
RL
250[ W]
1000
(EjsT04. 1)
Esta corriente circulará desde el nodo d hacia el nodo c (porque Vd > Vc: la corriente siempre circula
hacia potenciales decrecientes). Si consideramos el sentido positivo de Io hacia abajo (del punto c al
punto d, como se indica en la FIGURA T4. 1), entonces el valor que acabamos de hallar deberá ser
negativo:
(EjsT04. 2)
Io=-4 [mA] (cuando Vi<<0)
AHORA NOS PREGUNTAMOS: ¿Cuándo dejará de conducir D1 (diodo ideal)? Cuando el potencial en K1
sea mayor o igual que en A1. Si aumentamos Vi (lo hacemos menos negativo) para algún valor de
esta tensión se cumplirá VK1 > VA1, y D1 dejará de conducir.
Sin embargo,D2 seguirá en OFF, ya que VA2 < VK2
continuará siendo cierto.
Aplicando ley de voltajes a la malla a-f-e-d-c-b, teniendo en cuenta
que Io es la única corriente que circula por dicha malla,
podemos obtener la tensión Vi:
Vi - VRL - VR = Vi - IoRL - IoR = 0 Þ
Þ Vi = Io (RL + R) = -0,004[A] ( 250[W] + 750[W] ) = -0,004 ´ 1000[V] = -4[V]
(EjsT04. 3)
donde VRL es la tensión sobre RL y VR es la tensión sobre R.
SEGUNDO TRAMO: a partir de Vi = -4 [V], D1 y D2 se mantienen abiertos (porque las condiciones VK1 >
VA1 y VA2 < VK2 siguen siendo ciertas. La corriente Io es, entonces, aplicando la misma ecuación de
malla (EjsT04. 3):
Vi - IoRL - IoR = 0 Þ Io = Vi (RL + R) = Vi
( 250 + 750 ) [A]
Þ Io = Vi 1000[A] = Vi [mA] (cuando Vi ³ -4 [V])
I
(EjsT04. 4)
Una manera sencilla de recordar cuál es el ánodo y cuál el cátodo de un diodo, es considerar que la parte donde está el triángulo, que
se parece a una A, es el ánodo, y donde está la línea vertical, es el cátodo (se parece a una K invertida):
. Además, el triángulo
del diodo apunta hacia donde circula la corriente cuando está polarizado directamente, lo cual sucede cuando V A > VK.
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 3 DE 32
¿QUÉ SIGNIFICA ESTE ÚLTIMO RESULTADO? Que cuando Vi ³ -4 voltios, la corriente es numéricamente
igual (en miliamperios), a la tensión Vi (en voltios)II.
T ERCER TRAMO: Supongamos Vi >> 0 (i.e., Vi positiva, mucho mayor que cero). Ahora tendremos Va >>
Vf, y por lo tanto el potencial en el punto b será mayor que en el punto e (la tensión VR1 no tiene
influencia nuevamente, ya que es muy pequeña, en valor absoluto, comparada con Vi).
Consecuentemente, Vb > Ve Þ VK1 > VA1 (con VR1 pequeña) ÞD1 no conduce (D1 OFF).
Como hemos visto, Ve = Vd y Vb = Vc, entonces Vc > Vd Þ VA2 > VK2 (VR2 pequeña) Þ D2 ON.
Aplicando ley de Ohm sobre RL, tenemos:
Io =
Vc - Vd VR2
1[V]
4
[A] Þ Io = 4 [mA] (cuando Vi >> 0)
=
=
= 0,004 [A] =
RL
RL
250 [W]
1000
(EjsT04. 5)
El valor positivo se mantiene, puesto que Io esta vez circula desde c hacia d.
Reduciendo Vi obtendremos el caso límite cuando D2 deja de conducir:
Aplicando ley de voltajes a la malla a-b-c-d-e-f,
obtenemos la tensión Vi:
Vi - VR - VRL = Vi - IoR - IoRL = 0 Þ
Þ Vi = Io (RL + R) = 0,004[A] ( 250[W] + 750[W]) = 0,004 ´ 1000[V] = 4[V]
(EjsT04. 6)
Para Vi con valores menores de 4 [V], se aplica el mismo razonamiento que en el segundo tramo (los
dos diodos abiertos), obteniéndose, consecuentemente, una expresión idéntica a la (EjsT04. 4):
Vi - IoR - IoRL = 0 Þ Io = Vi (R + RL ) = Vi
( 750 + 250 ) [A]
Þ Io = Vi 1000 [A] = Vi [mA] (cuando Vi £ 4 [V])
(EjsT04. 7)
Ahora estamos en condiciones de representar Io= f(Vi) gráficamente, considerando los tres tramos:
II
Esto no significa que una corriente es igual a una tensión, ya que ambas son entidades distintas (la corriente indica movimiento de
cargas por unidad de tiempo, la tensión indica energía potencial por unidad de carga); significa que si medimos Vi en voltios e Io en
miliamperios, obtendremos el mismo valor numérico.
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 4 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
¿EN PALABRAS, QUÉ SIGNIFICA EL RESULTADO REPRESENTADO POR ESTA GRÁFICA?
El circuito de la FIGURA T4. 1 limita la corriente Io, manteniéndola entre -4 y 4 miliamperios para un
amplio rango de valores de la tensión de entrada Vi.
Por ejemplo:
· Si Vi = -5 voltios, Io = -4 miliamperios (punto A).
· Si Vi = 2 voltios, Io = 2 miliamperios (punto B).
· Si Vi = 6 voltios, Io = 4 miliamperios (punto C).
RESUMEN EJEMPLO 1 (T4):
DATOS:
R = 750 [W]; RL = 250 [W].
VR1 = VR2 = 1 [V].
D1 y D2 son diodos ideales.
INCÓGNITAS:
Io = f(Vi) = Corriente a través de RL en función de la tensión
de entrada Vi = ?
Representación gráfica de dicha función = ?
a) PRIMER T RAMO: Suponemos Vi << 0 Þ Ve > Vb Þ VA1 > VK1 Þ D1 ON,
además, Vd > Vc Þ VA2 < VK2 Þ D2 OFF
Io =
Vd - Vc VR1
1[V]
=
=
= 0,004[A] Þ Io = -4 [mA]
RL
RL
250 [W]
(EjsT04. 1)
(EjsT04. 2)
La corriente tiene sentido de d a c, por eso es negativa (se considera sentido de c hacia d como positivo).
Se aumenta Vi, hasta que se cumple VK1 > VA1 Þ D1 OFF, D2 OFF:
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 5 DE 32
Aplicando ley de mallas:
Vi = Io (R L + R) = -0,004[A] ( 250[ W] + 750[ W] ) = -4 [V]
(EjsT04. 3)
b) SEGUNDO T RAMO: Vi > -4 [V] Þ D1 OFF, D2 OFF (se mantienen abiertos).
Io = Vi (RL + R) = Vi
( 250 + 750 ) [A] Þ
Io = Vi [mA]
(EjsT04. 4)
c) T ERCER T RAMO: Suponemos Vi >> 0 Þ Vb > Ve Þ VK1 > VA1 Þ D1 OFF;
Vc > Vd Þ VA2 > VK2 Þ D2 ON.
Ley de Ohm sobre RL para obtener Io (apuntando desde c a d)
Io =
Vc - Vd VR2
1[V]
=
=
= 0,004 [A] Þ Io = 4 [mA ]
RL
RL
250 [W]
(EjsT04. 5)
Se reduce Vi hasta que se tiene D2 OFF:
Se aplica ley de voltajes a la malla a-b-c-d-e-f,
Vi - VR - VRL = Vi - IoR - IoRL = 0 Þ
Þ Vi = Io (RL + R) = 0,004[A] ( 250[W] + 750[W] ) = 4[V]
(EjsT04. 6)
Para Vi con valores menores de 4 [V], se aplica el mismo razonamiento que en el segundo tramo (los
dos diodos abiertos), obteniéndose nuevamente la ecuación (EjsT04. 4).
d) SE OBTIENE LA REPRESENTACIÓN GRÁFICA DE Io=f(Vi):
ES CONVENIENTE, PARA ASIMILAR CONCEPTOS CORRECTAMENTE (Y POR LO TANTO PARA FACILITAR EL ESTUDIO DE LA
ASIGNATURA), QUE RESUELVAS LOS PROBLEMAS Y ESTUDIES LA TEORÍA EMPLEANDO CONTINUAMENTE LAS
PREGUNTAS ¿QUÉ ES?, ¿QUÉ SIGNIFICA?, ¿CÓMO?, ¿POR QUÉ? (MÉTODO QCP).
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 6 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
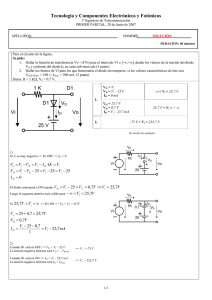
EJEMPLO 2 (T4):
En el circuito de la figura, suponiendo el diodo ideal y RL=100 [W], Vi(t) representa un
generador senoidal de 100 [V], 50 [Hz]. Calcular:
a) Valor de la máxima corriente en el circuito.
b) Dibuja la forma de onda de la tensión en la carga.
c) Tensión eficaz en la carga.
FIGURA T4. 2
PLANTEAMIENTO Y RESOLUCIÓN
a) ¿CÓMO SE OBTIENE LA CORRIENTE I(t) QUE CIRCULA SOBRE RL?
Como Vi(t) varía periódicamente con el tiempo, hay que analizar el circuito para averiguar cuándo D
conduce (VA > VK) y cuándo no lo hace (VA < VK); esto determinará el comportamiento de I(t). Una vez
determinado el comportamiento de I(t), se podrá establecer su valor máximo (o valor pico).
Un valor de Vi positivo significa que el potencial en el punto a es mayor que en d, es decir:
Vi(t)>0ÞVa>Vd. Eso implica que el potencial cae al pasar por D (y por RL), lo que implica VA>VK Þ D
ON, y la corriente tendrá el sentido de a hacia d, como lo indica la FIGURA T4. 2.
Como Vi(t) es una sinusoide, esto sucederá en el primer semiciclo (0 £ t < T/2):
Puesto que se considera que el diodo D es ideal,
cuando se encuentra conduciendo se comporta como
un interruptor cerrado; el circuito equivalente es
consecuentemente, para Vi(t) ³ 0:
Vemos que VL(t) = Vi(t). Aplicando ley de Ohm sobre RL:
VL (t) = I(t) RL Þ I(t) =
VL (t) Vi (t) Vm sen ( w t ) æ Vm ö
=
=
=ç
÷ sen ( w t ) cuando 0 £ t £ T/2.
RL
RL
RL
è RL ø
(EjsT04. 8)
Donde w = 2pf = 2´3,1416´50[Hz] = 314,16 [rad/seg] es la frecuencia angular.
A partir de t = T/2 y hasta t = T, la tensión Vi(t) será negativa:
entonces, si Vi(t) < 0 Þ Vd > Va
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 7 DE 32
con lo cual, en el circuito, desde el punto d hasta el punto a, la tensión irá disminuyendo, primero a
través de RL y luego a través de D.
CONCLUSIÓN: VK > VA Þ D OFF. Al quedar el circuito abierto, la corriente será
nula, como se indica en la figura de la derecha (nota el signo + en la fuente
Vi(t): está puesto en su borne inferior, ya que con eso se indica que la tensión
allí es, en este caso, mayor que la del borne superior).
I(t) = 0 cuando T/2 < t £ T (recuerda que T=1/f).
(EjsT04. 9)
Observamos entonces que, dependiendo del valor del tiempo t, la corriente I tiene dos expresiones:
ìæ Vm
ïç
I(t) = íè RL
ï
î0
ö
÷ sen ( w t ) = Im sen ( w t )
ø
cuando 0 £ t £ T/2
(EjsT04. 10)
cuando T/2 < t £ T
donde Im = Vm/RL es la amplitud de I(t) en el primer intervalo de tiempo.
Representando I(t) gráficamente, tenemos:
¿CÓMO SE OBTIENE EL VALOR MÁXIMO (PICO) DE LA CORRIENTE I(t)?
Observando esta última gráfica, o bien la ecuación (EjsT04. 10), deducimos que I(t) tiene un valor
máximo (valor de pico) igual a Im. Para calcular Im necesitamos el valor de Vm. En el enunciado no se
ha especificado si el voltaje establecido para Vi(t) era el valor máximo o el eficaz. Como convención,
si no se especifica, se presupone que es el Voltaje Eficaz, es decir, en este caso Vef = 100 [V]. De
resolver problemas de corriente alterna, sabemos que Vef = Vm/Ö2 Þ Vm = Ö2 Vef (para más
información, consulta el APÉNDICE I), de modo que la corriente máxima es:
Im =
Vm
=
RL
2 Vef 1,4142 ´ 100 [V]
=
Þ Im = 1,4142 [A]
RL
100 [W]
(EjsT04. 11)
b) ¿CÓMO SE OBTIENE LA TENSIÓN VL(t) EN LOS EXTREMOS DE RL?
Por RL circula I(t), por lo tanto, la tensión VL(t) sobre RL se obtiene aplicando Ley de Ohm, es decir:
ì éæ Vm ö
ù
ï êç
÷ sen ( w t ) ú RL = Vm sen ( w t )
VL (t) = I(t)RL = íêëè RL ø
ûú
ï
î0RL = 0
cuando 0 £ t £ T/2
(EjsT04. 12)
cuando T/2 < t £ T
En otras palabras: la forma de onda de VL(t) es la misma que I(t), aunque ambas difieren en la
amplitud:
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 8 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
¿QUÉ SIGNIFICA ESTE RESULTADO? Mientras que a la entrada tenemos una tensión Vi(t) que es
sinusoidal continua, la tensión sobre los extremos de RL -a la salida- sólo es media sinusoide. La
tensión VL(t) es, o bien positiva (en el intervalo 0 £ t <T) o bien cero (en el intervalo T/2 £ t < T). El
nombre RECTIFICADOR precisamente da la idea de que la tensión de entrada se ha “rectificado”
solamente hacia valores positivos.
c) ¿CÓMO SE OBTIENE LA TENSIÓN EFICAZ VLef SOBRE LA CARGA?
De lo que se expresa en el APÉNDICE I, podemos deducir que la definición de valor eficaz al cuadrado
de VL es el promedio de [VL(t)]2 en el intervalo 0 £ t < T. Esto se representa matemáticamente como:
2
VLef
=
1 T
2
[ VL (t)] dt
T ò0
(EjsT04. 13)
pero sólo hay que calcular esta integral en la primera mitad del intervalo (0 £ t < T/2), porque es en
ese rango, según lo indica la ecuación (EjsT04. 12), donde la VL(t) es distinta de cero. Resolviendo la
integral (aplicando un método similar al utilizado en el APÉNDICE I, o bien directamente usando la
fórmula 1.17.9, página 269, del libro Fórmulas y Tablas de Matemática Aplicada, de Spiegel, Serie
Schaum, segunda edición, año 2000), recordando que w = 2p/T, tenemos:
Int ervalo 0 £ t < T / 2
Int ervalo T / 2 £ t < T
=0
ì 64
4744
8 64
4744
8ü
6
474
8ü
ì
2
T
T
1 T
2
1 ï T/2
2
2
2pt ù
ï 1 ï T/2 2 é
ï
V = ò [ VL (t)] dt = í ò [ VL (t)] dt + ò [ VL (t)] dt ý = í ò Vm ê sen(
)ú dt + ò 02 dt ý =
T/2
0
T/2
T 0
Tï 0
T
T
ë
û
ï
ï
ï
î
þ
î
þ
=0
=0
ìé
64748
64748
ù é
ùü
T/2
ï
ê
ú
ê
é
æ 4p ö ù
æ 4p T ö
æ 4p ö ú ï
sen ç
t÷ú
sen ç
sen ç
0 ÷ úï
ï
2
2
÷ú ê
V2 ê t
V2 ïê T / 2
è T øú
è T 2 øú - ê0 è T ø ú ï = Vm æ T ö Þ V 2 = Vm
= mê = m íê
ý
Lef
ç
÷
8p
8p
8p
ú ê2
úï T è 4 ø
T ê2
T ïê 2
4
ú
ú ê
úï
ê
ú
T
T
T
ïê
ë
û0
ú ê
úï
ïî êëê
ûú ëê
ûú þ
2
Lef
(EjsT04. 14)
De modo que el valor de VLef es:
2
VLef
=
Vm2
V
Þ VLef = m =
4
2
2 Vef 1,4142 ´ 100 [V]
=
Þ VLef = 70,71 [V]
2
2
(EjsT04. 15)
donde, como hemos visto, Vef = 100 [V] es la tensión eficaz de la Vi(t) (tensión de entradaIII).
PREGUNTA: ¿ES VLef UNA FUNCIÓN QUE VARÍA CON EL TIEMPO?
No, VLef es un valor promedio de [VL(t)]2 en el intervalo 0 £ t <T. Es un valor de voltaje constante.
Para tener una idea más clara del significado de VLef e ILef, y su relación con la potencia consumida
por la resistencia de carga RL, consulta el APÉNDICE I.
III
Existe otro método para calcular la VLef. Como sobre RL circula I(t), es posible hallar primero el valor eficaz Ief =
V
1 T
2
[I(t)] dt = m
T ò0
2RL
-esta integral se calcula considerando (EjsT04. 10)-, y luego aplicar la ley de Ohm con valores eficaces: VLef = RL.Ief. El resultado,
según se observa, será el mismo.
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 9 DE 32
RESUMEN EJEMPLO 2 (T4):
DATOS:
Vi(t) = Vm sen(wt) = Ö2 Vef sen(2pf t);
Vef = 100 [V]; f = 1/T = 50 [Hz]; RL = 100 [W].
D es un diodo ideal.
INCÓGNITAS:
a) Im = Corriente máxima a través de RL = ?
b) Representación gráfica de VL(t) = ?
c) VLef = Tensión eficaz en la carga RL = ?
a) CORRIENTE MÁXIMA A TRAVÉS DE RL: Vi(t) > 0 (en el intervalo 0£t<T/2) Þ Va>VdÞVA>VK ÞD ON
I(t) =
VL (t)
RL
=
Vi (t)
RL
=
Vm sen ( w t )
RL
æV ö
Þ I(t) = ç m ÷ sen ( w t ) cuando 0 £ t £ T/2.
è RL ø
(EjsT04. 8)
La corriente I(t) tiene sentido de b a c, considerado como positivo.
Vi(t) < 0 (en el intervalo T/2 < t £T) Þ Va<VdÞVA<VK ÞD OFF:
I(t) = 0 cuando T/2 < t £ T (siendo T=1/f).
(EjsT04. 9)
Observando las ecuaciones (EjsT04. 8) y (EjsT04. 9), se deduce que el valor pico de I(t) es
Im =
Vm
=
RL
2 Vef 1,4142 ´ 100 [V]
=
Þ Im = 1,4142 [A]
RL
100 [W]
(EjsT04. 11)
b) REPRESENTACIÓN GRÁFICA DE LA TENSIÓN VL(t) SOBRE RL:
Por ley de Ohm, VL(t) = I(t) RL, y considerando las
ecuaciones (EjsT04. 8) y (EjsT04. 9), se obtiene:
C) T ENSIÓN EFICAZ
2
VLef
=
VLef EN LA CARGA RL: Aplicando la definición de valor eficaz, se obtiene:
V
1 T/2 2
2pt
Vm sen2 (
) dt Þ VLef = m =
T ò0
T
2
EJEMPLOS RESUELTOS DE TE
2Vef
=
2
2 100 [V]
= VLef = 70, 71 [V]
2
(EjsT04. 14)
(EjsT04. 15)
BRÉGAINS, IGLESIA, LAMAS
PÁG. 10 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
EJEMPLO 3 (T4):
Un generador sinusoidal de Vef = 100 [V] se conecta a un rectificador en puente de
diodos y a la salida de éste se conecta una carga RL = 200 [W]. Los diodos tienen los parámetros siguientes
Rf = 10 [W], Rr = ¥, Vg = 0,6 [V] y Vz = 300 [V]. Dibujar el circuito y calcular:
a) Valor de la corriente máxima Im por la carga.
b) Valores eficaz Ief y de continua Idc de la corriente en la carga.
c) Tensión inversa de pico VDinvp en un diodo.
d) Valor de continua de la corriente IDdc en los diodos.
e) Potencia PL disipada en la carga RL.
f) Valor de la tensión Vef,limite en el generador para la cual los diodos alcanzan su tensión
inversa máxima (tensión Zener).
PLANTEAMIENTO Y RESOLUCIÓN
DIBUJAMOS EL CIRCUITO: el rectificador se construye con cuatro diodos en puente (una manera de
recordar la configuración en puente, es considerar que conforman un rombo, con los cuatro diodos
apuntando hacia la derecha; los vértices superior e inferior del rombo entonces se conectan a la
fuente alterna de entrada; de esta manera, el vértice derecho indicará el potencial positivo de la salida
–la carga RL–, y el vértice izquierdo el potencial negativo).
FIGURA T4. 3
a) ¿CÓMO SE OBTIENE LA CORRIENTE I(t) QUE CIRCULA SOBRE RL?
Procedemos como en el punto a) del ejercicio anterior: analizamos el signo de Vi(t) = Vmsen(wt), para
determinar el comportamiento de los diodos, y, por tanto, de la corriente I(t).
Un valor de Vi(t) positivo sucede, como en el caso del ejemplo anterior, cuando 0 £ t < T/2. En ese
intervalo el potencial en el punto a es mayor que en d: Vi(t) > 0 Þ Va > Vd. Esto significa que el
potencial cae al pasar del punto a al punto d. Bajo este supuesto, el potencial cae al pasar del punto a
al punto b, o del a al c. Es decir:
ì Va > Vb Þ D1 conduce (D1 ON)
Vi (t) > 0 Þ Va > Vd Þ í
î Va > Vc Þ D4 apagado (D1 OFF)
(EjsT04. 16)
Razonando de modo análogo, tendremos:
ì Vb > Vd Þ D2 apagado (D2 OFF)
Vi (t) > 0 Þ Va > Vd Þ í
î Vc > Vd Þ D3 conduce (D3 ON)
(EjsT04. 17)
Para obtener el circuito correspondiente, cada diodo debe reemplazarse por su equivalente:
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 11 DE 32
Þ
D ON: resistencia Rf en serie con Vg:
D OFF: resistencia Rr = ¥, que es lo mismo que un circuito abiertoIV:
Þ
Observa que, en D ON, Vg se conecta con el borne + apuntando hacia el ánodo A.
Al realizar estos reemplazos, se obtiene, para Vi(t)>0:
Para hallar el valor de la corriente I(t), resolvemos la ecuación de la única malla disponible:
Vi - VD1 - VL - VD3
Þ I(t) =
Vi (t) - 2Vg
RL + 2R f
VD 1
VD 3
VL
64
4744
8 }
64
4744
8
= 0 Þ Vi - éëI(t)R f + Vg ùû - I(t)R L - éëI(t)R f + Vg ùû = 0
=
Vm sen( wt) - 2Vg
RL + 2R f
(EjsT04. 18)
en el intervalo 0 £ t < T / 2.
Esta corriente I(t) tiene sentido del punto b al punto c a través de la resistencia RL. En otras palabras: en la
ecuación anterior, Vi(t) prepondera sobre 2Vg, provocando que el potencial en b sea mayor que en el punto
c, haciendo que la corriente viaje en ese sentido.
También vemos en (EjsT04. 18) que esta I(t) alcanzará su valor pico cuando Vmsen(wt) sea máxima (ya que
los otros parámetros que intervienen en la ecuación son constantes). Como el valor máximo de Vmsen(wt)
es Vm, tendremos:
Þ Imax =
Vm - 2Vg
RL + 2Rf
=
2 Vef - 2Vg
RL + 2Rf
=
2 ´ 100[V] - 2 ´ 0,6[V]
Þ Imax = 0,637[A] .
200[W] + 2 ´ 10[W]
(EjsT04. 19)
en donde hemos recordado, que, para la tensión sinusoidal de entrada, Vef = Vm / Ö2 Þ Vm = Ö2 Vef.
Para Vi(t) < 0, en el intervalo T/2 £ t < T, aplicamos un razonamiento completamente análogo, obteniendo:
IV
Una resistencia infinita significa una oposición muy grande al paso de la corriente eléctrica, que es lo mismo que decir que el circuito
está abierto (no puede haber paso de corriente).
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 12 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
Analizando esta malla, vemos que la ecuación de la corriente es similar a la que se obtuvo
anteriormente (EjsT04. 18). En este caso, I(t) circula del punto b al punto c nuevamente, con lo cual
su sentido a través de RL no ha variado, a pesar de que el sentido de Vi(t) sí lo ha hecho (eso se
percibe si observamos las dos figuras anteriores de la izquierda). Para evitar el signo negativo que
aparecería de la función Vmsen(wt), escribimos la ecuación de malla utilizando valor absoluto de Vi(t):
Vi - VD1 - VL - VD3
Þ I(t) =
Vi (t) - 2Vg
RL + 2R f
VD 2
VD 4
VL
64
4744
8 }
64
4744
8
= 0 Þ Vi - éëI(t)R f + Vg ùû - I(t)R L - éëI(t)R f + Vg ùû = 0
=
Vm sen( wt) - 2Vg
RL + 2R f
(EjsT04. 20)
en el intervalo T/2 £ t < T.
En resumen, tenemos:
ì Vm sen( wt) - 2Vg
si 0 £ t < T / 2;
ï
RL + 2R f
ï
I(t) = í
ï Vm sen( wt) - 2Vg si T/2 £ t < T.
ï
RL + 2R f
î
(EjsT04. 21)
Vemos que el valor máximo de I(t) es el mismo que el calculado anteriormente.
b) ¿CÓMO SE OBTIENEN LOS VALORES EFICACES Ief Y DE CONTINUA Idc DE I(t)?
Aplicamos la definición de cada una. Idc es el promedio de I(t) en el intervalo 0 £ t < T, teniendo en
cuenta la ecuación (EjsT04. 21):
T
1 T
1 T/2
I(t)dt = é ò I(t) dt + ò I(t)dt ù =
ò
ê
úû
0
0
T
/2
T
Të
T é Vm sen( w t) - 2Vg ù
1 ïì T / 2 é Vm sen( wt) - 2Vg ù
ïü
= íò ê
ú dt ý =
ú dt + òT / 2 ê
0
T ïî
RL + 2R f
RL + 2R f
êë
úû ïþ
ë
û
Idc =
=
(EjsT04. 22)
1 ìï T / 2 é Vm sen( wt) - 2Vg ù üï
í2
ê
ú dt ý
T îï ò0 ë
RL + 2R f
û þï
Podemos resolver esta ecuación, pero antes haremos una simplificación. Como Vm >> 2Vg (de hecho,
2Vg = 1,2 [V] es del orden de menos del 1% de Vm = 141,42 [V]), podemos despreciar 2Vg de esta
última ecuación (no se cometerá mucho error al realizar esta simplificación), lo que hará que se
facilite el cálculo de la integral. Es decir:
Idc =
1 ìï T / 2 é Vm sen( w t) - 2Vg ù üï
1 ìï T / 2 é Vm sen( w t) ù üï
í 2 ò0 ê
ú dt ý Þ Idc » í 2 ò0 ê
ú dt ý =
T ïî
R L + 2R f
T ïî
ë RL + 2R f û ïþ
ë
û ïþ
T/2
T/2
2 Vm
2 Vm
2p
2p ù
é T
=
sen( t)dt =
cos( t) ú
ò
ê
0
T (RL + 2R f )
T
T (RL + 2R f ) ë 2p
T û0
=
(EjsT04. 23)
é 64748 64748 ù
2 Vm
2 Vm
T ê
2p T
2p ú
=
) + cos( 0)ú Þ Idc =
ê - cos(
T ú
T (RL + 2R f ) 2p ê
T 2
(RL + 2R f ) p
ëê
ûú
= ( -1)
=1
Asignando valores a los símbolos, tenemos:
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
Idc =
PÁG. 13 DE 32
2 Vm
2 ´ 2 ´ 100 [V]
=
Þ Idc = 0,409 [A]
(RL + 2R f ) p ( 200 [W] + 2 ´ 10[W] ) ´ 3,14159
(EjsT04. 24)
Observa que, si despreciamos 2Vg en la ecuación (EjsT04. 19), se obtiene:
Im ax =
Vm - 2Vg
(RL + 2R f )
»
Vm
Vm
2
æ2ö
Þ Idc » ç ÷
= Im ax
(RL + 2R f )
è p ø (RL + 2R f ) p
(EjsT04. 25)
que es una ecuación fácil de recordar para volver a utilizarla en circuitos rectificadores con diodos en
puente.
Para calcular Ief, procedemos de modo análogo, aunque hallando primero el promedio de [I(t)]2:
2
2
2
1 T
1 ïì T / 2 é Vm sen( wt) - 2Vg ù
ïü 2 ïì T / 2 é Vm sen(w t) ù
ïü
I(t)
dt
2
dt
dt ý =
=
»
[
]
í
ý
í
ê
ú
ê
ú
ò
ò
ò
T 0
Tï 0 ë
RL + 2R f
T ï 0 ë RL + 2R f û
û
î
þï
î
þï
=T / 4
644
47444
8
T/2
2Vm2
2Vm2
Vm
Vef
æTö
2 2p
=
sen
(
t)dt
=
Þ Ief =
=
÷
2 ò0
2 ç
T
2 ( RL + 2R f ) ( RL + 2R f )
T (RL + 2R f )
T ( RL + 2R f ) è 4 ø
Ief2 =
(EjsT04. 26)
Calculamos la Ief:
Ief =
Vef
I ö
100 [V]
æ
=
= 454,55 [V] ç además,Ief » max ÷
R L + 2R f 200 [W] + 2 ´ 10 [ W]
2ø
è
(EjsT04. 27)
Entre paréntesis se ha indicado el resultado con un razonamiento análogo al de la (EjsT04. 25).
c) CÁLCULO DE LA TENSIÓN INVERSA DE PICO A TRAVÉS DE CADA DIODO.
Primero, tenemos que especificar cuándo los diodos están polarizados en inversa, y luego hallar el
valor máximo de esas tensiones. Si se analiza un poco, se observará que todos los diodos reciben la
misma tensión inversa (aunque no al mismo tiempo). Por ejemplo, en la siguiente figura, cuando
V
Vi(t)>0, D2 está polarizado en inversa (conectado entre los puntos b y d, está en estado OFF) :
Teniendo en cuenta Vi(t), VD1 y VD2, vemos que:
Vi (t) - VD1 + VD2 = 0 Þ VD2 = + VD1 - Vi (t)
V
(EjsT04. 28)
Observa que VD1 y VD2 se miden desde el cátodo hacia el ánodo (la punta de la flecha está del lado del ánodo de cada diodo).
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 14 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
como VD1 es pequeña comparada con Vi(t), tendremosVI:
VD2 » - Vi (t)
en el intervalo 0 £ t < T / 2
(EjsT04. 29)
En el intervalo T/2 £ t < T, D2 está polarizado con tensión directa, de modo que la tensión pico inversa
sobre D2 es el valor máximo que alcanza en el intervalo especificado en la ecuación anterior, es decir:
VD2invp » - Vm = 141,42 [V]
(EjsT04. 30)
en donde se ha expresado en valor absoluto, ya que lo que importa es la amplitud, no el signo.
Si se analiza el comportamiento de los demás diodos, se obtendrá el mismo resultado: VD1invp = VD3invp
= VD4invp = 141,42 [V].
d) CÁLCULO DE LA CORRIENTE MEDIA (VALOR DE CONTINUA) EN CADA DIODO.
Los diodos D1 y D3 conducen durante medio periodo (0 £ t < T/2). En ese lapso circula por ellos la
corriente I(t). Luego, están abiertos el medio periodo restante (T/2 £ t < T), y por lo tanto la corriente a
través de cada uno es cero. Los diodos D2 y D4 siguen el proceso inverso. Por lo tanto, para el D1, por
ejemplo, teniendo en cuenta la ecuación (EjsT04. 21):
=0
6
474
8ù
é
T
1 T
1 ê T /2
ID1dc = ò I(t) dt = ê ò I(t) dt + ò 0 dt úú =
T/2
T 0
T 0
êë
úû
Idc
1 T / 2 é Vm sen( wt) - 2Vg ù
0,409 [A]
= ò ê
Þ ID1dc =
= 0,204 [A]
ú dt =
0
T
RL + 2R f
2
2
ë
û
(EjsT04. 31)
Con los demás diodos se obtiene el mismo resultado.
e) ¿CÓMO SE CALCULA LA POTENCIA DISIPADA EN LA RESISTENCIA DE CARGA RL?
Por definición (Ley de Joule), la potencia disipada por una resistencia es igual al valor eficaz al
cuadrado de la corriente que circula por ella, multiplicada por el propio valor de la resistencia: ILef2RL.
La corriente I(t) siempre circula a través de RL, por lo cual, ILef = Ief, es decir:
2
PL = ILef
RL = I2ef RL = ( 0,454 [A] ) 200 [ W ] Þ PL = 41,22[W ]
2
(EjsT04. 32)
Existe una alternativa a esta ecuación, y es hallar la tensión eficaz VLef en los extremos de la
2
resistencia, y luego aplicar la relación PL = VLef /RL. Se obtendría el mismo resultado.
¿QUÉ SIGNIFICA ESTE RESULTADO?
La resistencia consume 41,22 vatios, y esta potencia se transforma en calor. Para tener una idea
aproximada de esta magnitud de potencia, recordamos que existen bombillas de luz incandescente
que consumen 60 [W], de los cuales gran parte se transforma en calor y algo en luz para iluminar, por
ejemplo, una habitación. Es decir, si la resistencia a la salida del puente de diodos fuese una bombilla
incandescente (que trabajase a 100 Vef), sería capaz de iluminar perfectamente una habitación.
VI
Se podría hallar VD2 considerando que VD1 = I(t) Rf + Vg, con I(t) = [V m sen(wt) - 2Vg ] / (RL + 2 Rf). Aunque después de desarrollar las
ecuaciones, se llegaría a la misma conclusión.
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
f)
PÁG. 15 DE 32
SE PIDE CALCULAR LA TENSIÓN EFICAZ MÁXIMA DE LA FUENTE QUE PRODUCE RUPTURA DE LOS DIODOS.
En el punto d), hemos encontrado el valor de la tensión de pico inversa que soportan los diodos,
ecuación (EjsT04. 30):
VDinvp » - Vm = Vm
(EjsT04. 33)
Supongamos que variamos la Vef de la fuente Vi(t). La pregunta es, ¿cuál será la tensión eficaz
máxima que podemos establecer para dicha fuente (no sobrepasar la Vz de los diodos)? Para hallar
ese valor, simplemente especificamos, en la ecuación anterior, VDpinv = Vzener = Vz, que es la tensión de
pico inversa máxima que puede soportar cualquiera de los diodos. Recordando que, para el
generador con tensión sinusoidal Vef = Vm / Ö2, tendremos:
VDinvp = VZ » Vm,limite = 2 Vef,limite Þ Vef,limite =
VZ
2
=
300 [V]
Þ Vef,limite = 212,13 [V]
1,4142
(EjsT04. 34)
¿QUÉ SIGNIFICA ESTO?
Que si la tensión eficaz del generador sobrepasa los 212,13 voltios, los diodos del puente rectificador
corren el riesgo de estropearse, ya que sobrepasarán la tensión Zéner.
RESUMEN EJEMPLO 3 (T4):
DATOS:
Vi(t) = Vm sen(wt) = Ö2 Vef sen(2pf t);
Vef = 100 [V]; RL = 200 [W].
Parámetros de los diodos:
Resistencia en polarización directa: Rf = 10 [W]
Resistencia en polarización inversa: Rr = ¥ [W]
Tensión umbral en directa: Vg = 0,6 [V]
Tensión de ruptura (Zéner) en inversa: VZ = 300 [V]
INCÓGNITAS:
a) Im = Corriente máxima a través de RL = ?
b) Idc, Ief = Corrientes continua y eficaz a través de RL = ?
c) VDinvp = Tensión inversa de pico en los diodos = ?
d) Idc = Corriente continua (media) a través de los diodos = ?
e) PL = Potencia disipada en la carga = ?
f) Vef,limite = Tensión eficaz de la fuente Vi(t) con la que los
diodos alcanzan VZ = ?
a) CORRIENTE MÁXIMA A TRAVÉS DE RL: Vi(t) > 0 (en el intervalo 0 £ t < T/2) Þ Va > Vd, entonces:
ìVa > Vb Þ D1 ON;Va > Vc Þ D4 OFF
Vi (t) > 0 Þ Va > Vd Þ í
îVb > Vd Þ D2 OFF;Vc > Vd Þ D3 ON
EJEMPLOS RESUELTOS DE TE
(EjsT04. 16)
(EjsT04. 17)
BRÉGAINS, IGLESIA, LAMAS
PÁG. 16 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
VD1
VD 3
VL
64
4744
8 }
64
4744
8
Vm sen( wt) - 2Vg
é
ù
é
Vi (t) - ëI(t)R f + Vg û - I(t)RL - ëI(t)R f + Vg ùû = 0 Þ I(t) =
RL + 2R f
(0 £ t < T / 2).
(EjsT04. 18)
Para Vi(t) < 0, en el intervalo T/2 £ t < T, aplicamos un razonamiento completamente análogo, obteniendo:
VD 2
VD 4
VL
64
4744
8 }
64
4744
8
Vm sen( wt) - 2Vg
Vi (t) - éëI(t)R f + Vg ùû - I(t)RL - éëI(t)R f + Vg ùû = 0 Þ I(t) =
R L + 2R f
( T/2 £ t < T ).
(EjsT04. 20)
Por lo tanto, el máximo valor de I(t) en todo el intervalo (0 £ t < T) es:
Þ Imax =
Vm - 2Vg
RL + 2Rf
=
2 Vef - 2Vg
RL + 2Rf
=
2 ´ 100[V] - 2 ´ 0,6[V]
Þ Imax = 0,637[A] .
200[W] + 2 ´ 10[W]
(EjsT04. 19)
b) VALORES MEDIO Idc Y EFICAZ Ief DE I(t):
El valor medio de I(t) es:
Idc =
1 T
1 ïì T / 2 é Vm sen( wt) - 2Vg ù ïü 1 ïì T / 2 é Vm sen( wt) ù ïü
I(t)dt = í2ò ê
ú dt ý » í2ò0 ê
ú dt ý Þ
ò
0
T
T ïî 0 ë
RL + 2Rf
û ïþ T ïî
ë RL + 2R f û ïþ
Þ Idc =
2 Vm
2 ´ 2 ´ 100[V]
2
=
Þ Idc = 0,409[A] ; además, Idc » Imax
R
2R
3,14159
+
p
p
( L
f )
(EjsT04. 23)
(EjsT04. 24)
El valor eficaz de I(t) es:
I2ef =
=
2
üï 2 ìï T / 2 é V sen( wt) ù 2 üï
1 T
1 ìï T / 2 é Vm sen( wt) - 2Vg ù
2
m
I(t)
dt
=
2
dt
[
]
í
ý » í ò0 ê
ê
ú
ú dt ý =
T ò0
T ï ò0 ë
RL + 2R f
T
R
û
ë
L + 2R f û
ï
ï
î
þï
î
þ
Vm
2 (RL + 2R f )
Vef
I ö
100[V]
æ
Þ Ief =
=
= 454,55[V] ç además,Ief » m ax ÷
RL + 2R f 200[W ] + 2 ´ 10[W ]
2ø
è
(EjsT04. 26)
(EjsT04. 27)
c) T ENSIÓN INVERSA DE PICO A TRAVÉS DE CADA DIODO:
Para el análisis, es suficiente considerar el diodo D2 (análisis en el intervalo 0 £ t < T/2 Þ D2 OFF):
VD2 = + VD1 - Vi (t) » - Vi (t) Þ VD2invp » - Vm = 141,42 [V]
(EjsT04. 28)
(EjsT04. 29)
d) CORRIENTE MEDIA IDdc A TRAVÉS DE LOS DIODOS:
Para el análisis, es suficiente considerar el diodo D1 (0 £ t < T/2 Þ D1 ON, T/2 £ t < T Þ D1 OFF):
ID1dc =
Idc
1 T/2
1 T / 2 é Vm sen( wt) - 2Vg ù
0,409[A]
I(t)dt = ò ê
Þ ID1dc =
= 0,204 [A]
ú dt =
ò
T 0
T 0 ë
RL + 2R f
2
2
û
(EjsT04. 31)
e) POTENCIA PL DISIPADA EN LA RESISTENCIA DE CARGA RL:
Aplicamos Ley de Joule:
2
PL = ILef
RL = I2ef RL = ( 0,454 [A] ) 200 [ W ] Þ PL = 41,22[W ]
2
BRÉGAINS, IGLESIA, LAMAS
(EjsT04. 32)
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 17 DE 32
e) T ENSIÓN EFICAZ MÁXIMA DE LA FUENTE Vef,limite QUE PRODUCE RUPTURA DE LOS DIODOS:
Igualamos la tensión máxima límite a la tensión Zéner de cualquiera de los diodos:
VDinvp = VZ » Vm,limite = 2 Vef,limite Þ Vef,limite =
VZ
2
=
300 [V]
Þ Vef,limite = 212,13 [V]
1,4142
(EjsT04. 34)
EJEMPLO 4 (T4):
Un alimentador consta de un transformador de relación de transformación n = 10, un
puente de diodos (suponer diodos ideales), un filtro de condensador de capacidad C, y una carga que tiene
un consumo constante Idc = 5 [A]. Si la tensión de entrada al alimentador es Vef1 = 230 [V], trabajando a una
frecuencia f = 50 [Hz], se pide, además de dibujar un esquema del conjunto, calcular:
a) El valor de C necesario para obtener una tensión de rizado Vr = 1 [V] pico a pico.
b) Tensión continua a la salida del alimentador en las condiciones de b).
PLANTEAMIENTO Y RESOLUCIÓN
DIBUJAMOS EL CIRCUITO: consiste en un transformador conectado a la entrada del puente de diodos, y
un condensador en paralelo con una carga a la salida:
FIGURA T4. 4
En este caso, la Vi(t) especificada en la FIGURA T4. 3 será V2(t).
a) ¿CÓMO CALCULAMOS EL VALOR DE C PARA QUE EL RIZADO SEA Vr = 1 VOLTIO PICO A PICO?
Debemos saber primeramente qué es la tensión de rizado. Si el condensador C no estuviese
presente, la tensión sobre ZL sería la tensión Vi(t) rectificada, es decir, VL(t) = | Vi(t) | = | V2(t) | =
|_V2msen(wt) |, considerando que no hay caída de tensión en los diodos (no hay caída de tensión
umbral Vg = 0, ni caída en las resistencias en directa Rf = 0), porque los diodos D1 a D4 se consideran
ideales. Si se conecta el condensador C, en los extremos de éste también habrá la tensión VL(t),
puesto que C y ZL están en paralelo. Como C almacena carga en sus placas, hará que la tensión
varíe más lentamente (ya que tiene que cargarse y descargarse conforme pasa el tiempo). Eso hace
que la variación de VL(t) sea menos pronunciada. La tensión de rizado es la diferencia entre el valor
máximo y el valor mínimo que alcanza VL(t) cuando C está conectado. Lo dicho se observa en la
siguiente gráfica:
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 18 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
Para calcular el valor de Vr, analicemos, de las últimas figuras, la de la derecha. En ella vemos que
desde t = T/4 hasta t = T/4 + t2, la tensión del capacitor disminuye. Llamemos DVL a esa disminución
de voltaje, que es precisamente Vr, es decir: DVL = Vr. Esto sucede porque, en ese lapso, C pierde
carga. Llamemos DQ a esa pérdida de carga. Como, por definición, la corriente es paso de cargas a
través de un conductor en la unidad de tiempo, entonces, en t2 segundos han pasado DQ Culombios
por C. Como aproximación, DQ dividido por t2 tiene que ser igual a Idc (la corriente en la carga es
constante, y en este caso, dicha corriente es debida a la cesión de cargas por parte de C), es decir:
Idc = Corriente por C =
Cargas que pasaron por C en el lapso t 2 Dq é Coulombios ù
=
t 2 êë segundo úû
Lapso t 2
(EjsT04. 35)
De aquí podemos despejar Dq = Idc.t2. Pero además, por definición, el voltaje en los extremos del
condensador C es VC = q/C = VL. Con lo cual, si q varía, VL variará en la misma proporción (C es
constante): DVL = Dq/C. Por lo tanto:
DVL =
I t
Dq
Þ DVL = dc 2 = Vr
C
C
(EjsT04. 36)
De la misma figura que estamos analizando vemos que t2 es aproximadamente igual a T/2, y
además, T = 1 / f. Entonces:
Vr =
Idc t2 Idc T
I
I
5 [A]
»
= dc Þ C = dc =
Þ C = 0,05[F] = 50000 [m F]
C
2C 2f C
2 f Vr 2 ´ 50 [Hz] ´ 1[V]
(EjsT04. 37)
¿QUÉ SIGNIFICA ESTE RESULTADO?
Que para obtener un rizado de 1 voltio, hay que conectar a la salida de este circuito un condensador
de 50000 [mF]. Si se conecta un capacitor más pequeño, se tendrá un rizado más grande (ya que la
tensión de rizado es inversamente proporcional a C, según se observa en la ecuación anterior).
PREGUNTA: ¿POR QUÉ T = 1 / f?
La frecuencia f indica el número de veces que la Vi(t) completa su ciclo por unidad de tiempo. Es
decir, f = 50 [Hz] = 50 [ciclos/seg] significa que en 1 segundo la tensión oscila 50 veces (se repiten 50
sinusoides). El periodo T indica, por otra parte, la duración de cada sinusoide. Por lo tanto, en este
caso específico, si se tienen 50 ciclos en 1 segundo, entonces hay que dividir 1 segundo por 50 para
saber cuánto dura cada ciclo Þ T = 1/f = 1/50 = 0,02 [seg], que es la relación entre T y f que se
especifica siempre.
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 19 DE 32
b) ¿CÓMO CALCULAMOS EL VALOR MEDIO DE LA TENSIÓN VL(t)?
Según la figura de la derecha, el valor promedio de VL(t), al que
llamamos Vdc, se puede aproximar a:
Vdc = V2m -
Vr
2
(EjsT04. 38)
Para hallar el valor de V2m, utilizamos la definición de relación de transformación n (tensión de entrada
V1 del transformador partida por la tensión de salida V2):
n=
V1(t) V1m sen ( wt ) V1m
V
=
=
Þ V2m = 1m =
V2 (t) V2m sen ( wt ) V2m
n
2 V1ef
Þ V2m =
n
2 ´ 230[V]
= 32,5[V]
10
(EjsT04. 39)
¿QUÉ SIGNIFICA ESTE RESULTADO?
Como la relación de transformación es n=10, al pasar del primario al secundario, la tensión se ha
reducido en esa proporción. Este tipo de configuración se denomina Transformador Reductor, porque
al pasar del primario al secundario la tensión se reduce (las otras opciones serían Transformador
Elevador, cuando n < 1, y Transformador Separador, cuando n = 1, ya que en este último caso no
varía la tensión al pasar del primario al secundario: sólo se separan eléctricamente, y quedan
acopladas magnéticamente –el transformador es eso: un acoplador magnético–).
En esta ecuación, hemos podido simplificar las expresiones sen(wt), porque ambas tensiones
comparten la misma frecuencia angular w (esta es una característica de los transformadores ideales:
la frecuencia del voltaje de salida es la misma que la del voltaje de entrada).
Reemplazando este valor en la fórmula anterior, tenemos:
Vdc = V2m -
Vr
1[V]
= 32,5[V] Þ Vdc = 32[V]
2
2
(EjsT04. 40)
¿QUÉ SIGNIFICA ESTE RESULTADO?
Que, en promedio, la tensión de salida tendrá 32 voltios, pero oscilará entre 32,5 voltios (Vdc + Vr/2) y
31,5 voltios (Vdc - Vr/2). Esa variación de ± Vr/2 = ± 0,5 [V] se debe a la carga y descarga continua del
condensador C.
PREGUNTA: SI NO TUVIESE CONDENSADOR C, ¿CUÁL SERÍA LA TENSIÓN DE RIZADO?
Sin condensador, la tensión de salida oscila entre 0 [V] y V2m= 32,5 [V], o sea que Vr = V2m = 32,5 [V].
La idea de conectar C se basa en la reducción de dicha oscilación, de manera que la tensión de
salida se parezca lo más posible a una fuente de voltaje constante.
Un circuito rectificador ideal sería aquél que a la entrada se conecta una tensión variable (sinusoidal
en este caso), y a la salida se obtiene una tensión invariable, continua, como la de una pila (también
ideal). Los cargadores de los móviles y de los portátiles tienen esa configuración básica: un
transformador en el que el primario se conecta a la red de alimentación (de 220 [V] eficaces), en el
secundario se obtiene una tensión alterna reducida (puede ser de 9 [V] eficaces, por ejemplo), ésta se
rectifica (en onda completa) mediante un puente de diodos, y luego la tensión se filtra a través de un
condensador, en algunos casos incluyéndose un diodo Zéner estabilizador.
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 20 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
RESUMEN EJEMPLO 4 (T4):
DATOS:
V1(t) = Tensión sinusoidal conectada al primario
= Vm sen(wt) = Ö2 Vef sen(2pf t);
V1ef = Tensión eficaz en el primario del
transformador = 230 [V];
f = Frecuencia del voltaje = 50 [Hz]
n= Relación de transformación = 10;
D1 a D4: Diodos ideales
Idc = Corriente continua por la carga = 5 [A].
Vr = Tensión de rizado (de VL)= 1 [V] pico a pico.
INCÓGNITAS:
C= Valor de la capacidad del condensador para la
tensión de rizado Vr = ?
Vdc = Valor de continua de la tensión de salida = ?
a) VALOR DE C PARA OBTENER UNA TENSIÓN DE RIZADO Vr = 1 [V]:
Consideramos que por C circula la Idc = 5 [A]. Llamando Dq a la
carga adquirida por C en el intervalo de descarga t2 » T/2 (ver
figura de la derecha), y considerando que T = 1/f, se tiene:
Idc =
=
I t
I T
I
I
Dq
Dq
, pero Vr =
Þ Vr = dc 2 = dc = dc Þ C = dc =
t2
C
C
2C 2f C
2 f Vr
5 [A]
Þ C = 0,05[F] = 50000 [mF]
2 ´ 50 [Hz] ´ 1[V]
(EjsT04. 35)
(EjsT04. 36)
(EjsT04. 37)
b) VALOR MEDIO DE LA TENSIÓN VL:
n=
V1m
V
Þ V2m = 1m =
V2m
n
Vdc = V2m -
BRÉGAINS, IGLESIA, LAMAS
2 V1ef
Þ V2m =
n
2 ´ 230 [V]
= 32,5 [V]
10
Vr
1[V]
= 32,5[V] Þ Vdc = 32[V]
2
2
(EjsT04. 39)
(EjsT04. 40)
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 21 DE 32
EJEMPLO 5 (T4):
Un generador de 220 [V] eficaces se conecta a un rectificador en puente de diodos y la
salida de éste a una carga RL = 270 [W]. Los diodos son ideales. Calcular:
a)
b)
c)
d)
e)
FIGURA T4. 5
Valor de la Imax por la carga
Valor de Ief e Idc en la carga
Tensión inversa de pico en un diodo
Idc e Ief en cada uno de los diodos
Potencia disipada en la carga.
PLANTEAMIENTO Y RESOLUCIÓN
Este problema se resuelve con un procedimiento similar al utilizado en el Ejemplo 3 (T4).
a) VALOR DE LA CORRIENTE MÁXIMA Imax POR LA CARGA RL:
Directamente utilizamos la expresión de la corriente que habíamos hallado anteriormente, ecuación
(EjsT04. 19), página 11. Como en el enunciado se indica que D1 a D4 son diodos ideales
consideramos Vg = 0 (los diodos no tienen tensión umbral) y Rf = 0 (no tienen resistencia cuando están
conectados en directa). Por lo tanto, teniendo en cuenta que la Vef de entrada es de 220 [V]:
Imax =
Vm - 2Vg
RL + 2Rf
=
2 Vef - 2Vg
RL + 2Rf
=
2 220[V] - 2 ´ 0[V]
Þ Imax = 1,15[A]
270[W] + 2 ´ 0[W]
(EjsT04. 41)
PREGUNTA: ¿QUÉ SIGNIFICA QUE Rf = 0 Y Vg = 0?
El diodo conduce cuando el potencial en el ánodo VA es mayor que el potencial en el cátodo VK, es
decir VA > VK. ¿En qué medida tiene VA que ser mayor que VK? En un valor Vg. Si al pasar del punto A
al punto K el potencial cae, entonces podemos pensar que, cuando el diodo empieza a conducir
(todavía no existe corriente por él), VK se obtiene restando de VA el valor Vg, es decir: VK = VA-Vg. Por
otra parte, si se considera que el diodo tiene resistencia interna Rf, cuando empieza a circular una
corriente I(t) por el diodo, por Ley de Ohm, aparecerá una caída de potencial adicional entre A y K,
igual a I(t)´Rf, es decir:
…se obtiene restando al potencial del ánodo
El potencial en el cátodo
…las caídas debidas al umbral Vg y a la Rf
VK = VA - Vg - I(t)Rf
(EjsT04. 42)
Unos valores Vg = 0, y Rf = 0, significa que, en conducción VA = VK (según se deduce de la ecuación
anterior), con lo cual no hay caída de potencial en el diodo, es decir, se comporta como un simple
interruptor, que es la definición de diodo ideal.
b) VALOR DE LAS CORRIENTES MEDIA Idc Y EFICAZ Ief POR LA CARGA RL:
Para la corriente media podemos utilizar la simplificación hecha en la (EjsT04. 25), página 13:
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 22 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
Idc =
2
2
Im ax =
´ 1,15[A] = 0,732 [A]
3,1415
p
(EjsT04. 43)
y para la corriente eficaz, la simplificación establecida en la (EjsT04. 27), página 13:
Ief =
Im ax
=
2
1,15 [A ]
= 0,813 [A ]
1,4142
(EjsT04. 44)
c) VALOR DE LA TENSIÓN DE PICO INVERSA EN CUALQUIERA DE LOS DIODOS:
Ecuación (EjsT04. 30), página 14:
VDinvp = - Vm =
2 Vef = 1,4142 ´ 220 [V] = 311,12[V]
(EjsT04. 45)
donde el subíndice D se refiere a cualquiera de los diodos D1 a D4.
d) CORRIENTES MEDIA IDdc Y EFICAZ IDef EN LOS DIODOS:
La corriente media se obtiene aplicando la (EjsT04. 31), página 14:
IDdc =
Idc 0,732 [A]
=
= 0,366 [A]
2
2
(EjsT04. 46)
Recordando que cada uno de los diodos conduce sólo la mitad del periodo y utilizando el mismo
procedimiento que en la ecuación (EjsT04. 26), página 13, el valor de la corriente eficaz por cada uno
de los diodos resulta ser:
2
IDef
2
=0
ì
}
=0
é
ù
6
474
8 üï
2
ï
T
V2
1 ï T / 2 ê Vm sen( wt) - 2 Vg ú
ï 1 ïì T / 2 é V sen( wt) ù
ïü
dt + ò 0 2 dt ý = í ò ê m
dt ý = m2 Þ
= íò ê
ú
ú
T /2
0
Tï 0 ê
RL + 2R f
RL
4RL
ë
û
ï T îï
ú
{
þï
=0
ë
û
îï
þï
Þ IDef =
(EjsT04. 47)
Vm
I
1,15[A]
= max Þ IDef =
= 0,675[A]
2RL
2
2
e) POTENCIA DISIPADA EN LA CARGA RL:
Se obtiene utilizando la ley de Joule, ecuación (EjsT04. 32), página 14:
2
PL = ILef
RL = I2ef RL = ( 0,813 [A] ) 270[ W ] Þ PL = 178,46 [W ]
2
(EjsT04. 48)
RESUMEN EJEMPLO 5 (T4):
ESTE EJEMPLO NO REQUIERE RESUMEN.
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 23 DE 32
EJEMPLO 6 (T4):
El circuito de la figura utiliza un diodo Zéner para limitar la tensión que se aplica a la
carga RL procedente de un rectificador en puente de diodos (Características del Zéner: Vg = 0 [V], VZ = 12
[V], Rf = 100 [W], RZ = 0 [W], Rr®¥ [W]; Características de los diodos del rectificador: Vg = 0 [V], Rf = 50 [W],
Rr®¥ [W]).
FIGURA T4. 6
Para una tensión de entrada Vi de 20 voltios eficaces:
a) Si no existiera el Zéner, determinar los valores de tensión continua y eficaz en la
carga RL.
b) Con el diodo Zéner, establecer:
i. Formas de onda de tensión y corriente en la carga para un ciclo de la tensión
de la entrada Vi(t), indicando los valores instantáneos de interés.
ii. Expresión integral completa a través de la cual se determinan los valores de
tensión continua y eficaz en la carga.
PLANTEAMIENTO Y RESOLUCIÓN
a) ¿CÓMO SE CALCULAN LAS TENSIONES VLdc Y VLef CUANDO NO SE CONECTA EL DIODO ZÉNER?
El circuito es equivalente a un rectificador en
puente sin filtro, con la particularidad de que, como
carga, existe una resistencia RS en serie con RL:
Para analizar este circuito razonamos teniendo en
cuenta los resultados obtenidos en el EJEMPLO 3 (T4), página 10. Por ejemplo, si Vi(t)>0, tendremos
el siguiente circuito equivalente:
Teniendo en cuenta que RS está en serie con RL, y que Vg = 0, la
corriente media es, de acuerdo a la ecuación (EjsT04. 19):
2 Vm
2 ´ 2 ´ Vef
æ2ö
Idc = ç ÷ Im ax =
=
p (RS + RL + 2R f ) (RS + RL + 2R f ) p
èpø
EJEMPLOS RESUELTOS DE TE
(EjsT04. 49)
BRÉGAINS, IGLESIA, LAMAS
PÁG. 24 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
Es decir:
Idc =
2´ 2 ´ Vef
2´ 1,4142 ´ 20[V]
=
= 0,03[A]
(RS + RL + 2Rf ) p (100[W] + 400[W] + 2 ´ 50[W]) 3,1416
(EjsT04. 50)
El mismo resultado se obtiene para Vi(t) < 0.
Como por ley de Ohm VL(t) = I(t)´RL entonces:
T
1 T
R LI(t)dt = R L é ò I(t)dt ù = R LIdc Þ VLdc = 400 [W] ´ 0,03[A] = 12,0 [V ]
ò
0
0
ê
úû
ë
T
De modo análogo, para la Ief y el VLef tendremos:
VLdc =
Ief =
Vef
20 [V]
Þ Ief =
= 0,033[A]
(RS + RL + 2R f )
(100[W] + 400 [W] + 2 ´ 50[ W] )
VLef = Ief ´ R L = 0,033 [A ] ´ 400 [ W ] Þ VLef = 13,33 [V ]
(EjsT04. 51)
(EjsT04. 52)
(EjsT04. 53)
¿QUÉ PODEMOS DEDUCIR DE ESTAS ÚLTIMAS CUATRO ECUACIONES?
Que se puede aplicar la ley de Ohm directamente con valores medios y eficaces: VLdc=ILdc´RL,
VLef=ILef´RL. Esto resulta evidente. Por ejemplo, observa la ecuación (EjsT04. 51): el hecho de que RL
sea constante hace que se pueda extraer de la integral, con lo cual se puede hallar Idc por separado,
obteniéndose VLdc = RL Idc. Lo mismo sucede con el valor eficaz del voltaje.
b) ¿CÓMO SE CALCULAN I(t) Y VL(t) CUANDO SE INCLUYE EL DIODO ZÉNER?
El Zéner puede conducir cuando está conectado en directa (si VA-VK sobrepasa la tensión umbral Vg),
como un diodo “normal”, y cuando está conectado en inversa (si VK-VA sobrepasa la tensión Zéner
VZ), en la zona Zéner. Esto último no puede hacerse con un diodo normal, sin riesgo de estropearse.
Sin embargo, el Zéner se utiliza cuando está polarizado en inversa: la corriente que circula por él irá
desde el cátodo hacia el ánodo (sentido contrario al de un diodo normal). Analizamos el circuito con
DZ conectado:
El Zéner puede tener uno de tres estados:
·
Si VA>VK, estará en estado de conducción, como un diodo “normal” polarizado en directa.
Entonces, tendrá que reemplazarse por una resistencia Rr en serie con una fuente Vg. En este
caso, como Rr = 0 y Vg = 0, entonces, el DZ es equivalente a tener un cortocircuito.
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
·
PÁG. 25 DE 32
Si VA<VK estará polarizado en inversa. El valor de la diferencia entre VK y VA determinará si
está en estado “apagado” (VK - VA < VZ, la diferencia es menor), o en estado Zéner (VK - VA >
VZ, la diferencia es mayor).
Analizamos el circuito, ver figura anterior:
El extremo (+) del rectificador (punto b) siempre tiene mayor potencial que el extremo (-) (punto c),
por lo que el potencial cae al pasar por los puntos f = e y g = h, y por lo tanto:
Vb > Ve > Vh
Como conclusión, en este circuito DZ siempre está polarizado en inversa: VK > VA. De acuerdo a que
acabamos de comentar, DZ tendrá dos estados:
1) Cuando la diferencia de potencial entre e y h (y por lo tanto entre K y A) no sobrepasa la tensión
Zéner VZ = 12 Voltios, DZ se encuentra en estado abierto (porque la resistencia en inversa es
muy grande Rr = ¥, una resistencia muy grande no deja pasar ninguna corriente: abierto):
VK > VA pero
VK - VA < VZ
CONCLUSIÓN PARCIAL: cuando VK-VA = Ve-Vh = VL es menor que VZ, es como si DZ no existiese.
2) Cuando la diferencia de potencial entre e y h (y por lo tanto entre K y A) sobrepasa la tensión
Zéner VZ = 12 Voltios, DZ se encuentra en estado Zéner [es equivalente a que aparezca una
resistencia RZ (=0 en este problema) en serie con una fuente VZ entre K y A (el extremo +
apuntando hacia K)], es decir:
VK > VA y
VK - VA > VZ
CONCLUSIÓN PARCIAL: cuando VK-VA = Ve-Vh = VL es mayor que VZ, es como si DZ se convirtiese
en una fuente que fija el potencialVII entre los puntos f y g, es decir VL = constante = 12 [V].
Con este análisis ya estamos en condiciones de dibujar la forma de onda de VL(t):
VII
RECUERDA: las fuentes de tensión imponen su voltaje entre los extremos a los que está conectada, mientras que las fuentes de
corriente imponen su corriente por la rama a la que pertenecen. COROLARIO: dos fuentes de tensión no pueden conectarse en paralelo,
ni dos fuentes de corriente conectarse en serie, porque ello significaría que el circuito tiene problemas (por ejemplo, si conectamos dos
fuentes V1 = 10 [V] y V2 = 12 [V] en paralelo, tendríamos dos tensiones distintas entre sus dos extremos, lo cual producirá cortocircuito).
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 26 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
Los puntos de interés en la gráfica de la derecha son 1 y 2: son los instantes entre los cuales DZ está
en zona Zéner, cumpliéndose, según se observa, lo siguiente:
æ 2p ö
æ 2p ö
VLm sen ç
t ÷ = VZ Þ R LImax sen ç
t ÷ = VZ
T
è
ø
è T ø
(EjsT04. 54)
Pero de la ecuación (EjsT04. 49), tenemos que Imax = p Idc / 2, entonces:
400 [W ] ´ 3,1416 ´ 0,03 [ A ]
R L p Idc
æ 2p ö
æ 2p ö
sen ç
t ÷ = VZ Þ
sen ç
t ÷ = 12 [ V ]
2
2
è T ø
è T ø
(EjsT04. 55)
De donde podemos despejar t, obteniendo dos soluciones (que corresponden a los puntos 1 y 2):
12
2p
æ 2p ö
æ 2p ö
= 0,6366 Þ
18,84 sen ç
t ÷ = 12 Þ sen ç
t÷ =
t = arcsen ( 0,6366 ) Þ
T
è T ø
è T ø 18,84
0,69 T
ì
ì t1 = 0,11 T
ïï t1 = 2p
ì0,69
2p
ï
Þ
Þí
Þí
t=í
T
î p - 0,69 = 2,45
ï t = 2,45 T
îï t 2 = 0,39 T
2
îï
2p
(EjsT04. 56)
Ahora resulta sencillo hallar la corriente I(t) = VL(t)/RL. Como RL es constante, la forma de la curva no
cambiará:
Los valores relevantes de I(t) son:
VLm 18,84 [ V ]
=
= 0,047[A] = Im ax
RL
400 [ W ]
12 [ V ]
VZ
=
= 0,03[A]
RL 400 [ W ]
(EjsT04. 57)
c) ¿CUÁLES SON LAS EXPRESIONES DE LAS TENSIONES CONTINUA VLdc Y EFICAZ VLef EN LA CARGA?
La función VL(t) se repite en los intervalos 0 £ t < T/2 y T/2 £ t < T, o sea que integrar VL entre 0 y T es
lo mismo que duplicar la integral entre 0 y T/2. Otro modo de verlo es el siguiente: el área bajo la
curva entre 0 y T – o sea la integral- es lo mismo que 2 veces el área bajo la curva entre 0 y T/2.
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
VLdc =
PÁG. 27 DE 32
1 T
2 T/2
VL (t) dt = ò VL (t)dt
T ò0
T 0
(EjsT04. 58)
Entre 0 y T/2, VL(t) se expresa como:
ì VLm sen ( wt )
ï
VL (t) = í VZ
ï V sen wt
( )
î Lm
0 £ t < t1
t1 £ t < t 2
(EjsT04. 59)
t2 £ t < T / 2
Entonces, separamos la integral entre 0 y T/2 en tres tramos:
t2
T/2
2 é t1
VLm sen ( wt ) dt + ò VZ dt + ò VLm sen ( wt ) dt ù Þ
ò
ê
0
t
t
úû
1
2
Të
t1
t2
t1
t2
2
2
Þ VLdc = é 2VLm ò sen ( wt ) dt + ò VZ dt ù = é 37,68 ò sen ( wt ) dt + 12 ò dt ù
ê
0
t
ú
ê
0
t
úû
1
1
û Të
Të
VLdc =
(EjsT04. 60)
en donde hemos tenido en cuenta que el área bajo la curva entre 0 y t1 es la misma que entre t2 y T/2.
Con la tensión eficaz se procede de modo análogo:
2
=
VLef
t1
t2
1 T
2 T/2
2
2
2
2
VL (t)] dt = ò [ VL (t) ] dt = é 2VLm
sen2 ( wt ) dt + VZ2 ò dt ù Þ
[
ò
ò
úû
0
t1
T 0
T 0
T ëê
2é
2 t1
2 t2
Þ VLef =
2 (18,84 ) ò sen2 ( wt ) dt + (12 ) ò dt ù
0
t1
ûú
T ëê
(EjsT04. 61)
PREGUNTA: ¿QUÉ RESULTADOS DARÍAN ESTAS INTEGRALES? En principio, dependerían del valor de T,
que no se ha dado. Sin embargo, existe un truco para resolverlas: sustituir variables. Si en las
ecuaciones anteriores hacemos a = wt Þ da/dt = w Þ da = w dt = (2p/T) dt, podremos resolverlas,
reemplazando t®a/w, dt®da/w, y hallando previamente los valores correspondientes a a1 y a2:
æ 2p ö
a1 = w t 1 = ç
÷ 0,11´ T = 0,11´ 2 ´ p = 0,69 [rad]
è T ø
æ 2p ö
a 2 = wt 2 = ç
÷ 0,39 ´ T = 0,39 ´ 2 ´ p = 2,45 [rad]
è T ø
(EjsT04. 62)
Vemos que, según las unidades, se pasa de trabajar con variables temporales (t en segundos) a
trabajar con variables angulares (a en radianes). En muchos libros de electrónica, los cálculos de las
integrales de valor medio y de valor eficaz, y las gráficas de las funciones, se indican con a como
variable en lugar de t. Esto suele facilitar los cálculos, pero algunas veces puede confundir al alumno
principiante. Como ejemplo podemos calcular el valor medio VLdc con dicho cambio de variable:
dt 8
dt 8
6
474
6
474
é
ù
wt
}
a
a
a1
a2
ê
2
da
da ú 1 é
1
2
VLdc = ê 2VLm ò sen ( a )
+ ò VZ
=
2VLm ò sen ( a ) da + VZ ò da ù Þ
ú
0
a
ê
0
a
úû
1
Tê
( 2 p T ) 1 ( 2p T ) ú p ë
ë
û
a1
a2
1é
Þ VLdc = ê 2VLm ( - cos a ) 0 + VZ ( a ) a ùú =
1 û
pë
1
é 2 ´ 18,84 ( - cos 0,69 + cos 0 ) + 12 ( 2,45 - 0,69 ) ûù Þ VLdc = 9, 46 [V]
=
3,1416 ë
EJEMPLOS RESUELTOS DE TE
(EjsT04. 63)
BRÉGAINS, IGLESIA, LAMAS
PÁG. 28 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
RESUMEN EJEMPLO 6 (T4):
DATOS:
Vi(t) = Tensión sinusoidal de entrada = Vm sen(wt)
= Ö2 Vef sen(2pf t);
Vef = Tensión eficaz de entrada = 20 [V];
RS = Resistencia en serie = 100 [W]
RL = Resistencia de carga = 400 [W]
CARACTERÍSTICAS DEL ZÉNER DZ:
Vg = Tensión umbral en directa = 0 [V],
Rf = Resistencia en directa = 100 [W],
Rr = Resistencia en inversa = ¥ [W] (circ. abierto);
VZ = Tensión Zéner = 12 [V]
RZ = Resistencia en Zéner = 0 [W] (cortocircuito),
CARACTERÍSTICAS DE LOS DIODOS RECTIFICADORES:
Vg = Tensión umbral en directa = 0 [V],
Rf = Resistencia en directa = 50 [W],
Rr = Resistencia en inversa = ¥ [W] (circ. abierto)
INCÓGNITAS:
VLdc = Tensión media en la carga sin DZ = ?
VLef = Tensión eficaz en la carga sin DZ = ?
VL(t) = Forma de onda voltaje en RL con DZ = ?
I(t) = Forma de onda corriente en RL con DZ = ?
Expresiones de las integrales para hallar VLdc y VLef
con DZ = ?
a) T ENSIONES VLdc Y VLef SOBRE RL SIN DZ: Vi(t) > 0 (en el intervalo 0 £ t < T/2) Þ Va > Vd, entonces:
Corriente media por la carga, (EjsT04. 49) y (EjsT04. 50):
2 ´ 2 ´ Vef
æ2ö
Idc = ç ÷ Im ax =
Þ
(RS + RL + 2Rf ) p
è pø
Þ Idc =
2 ´ 1,4142 ´ 20[V]
= 0,03[A]
100[
W
]
+
400[W] + 2 ´ 50[ W] ) 3,1416
(
Vi(t)< 0 se analiza de modo análogo.
La tensión media sobre RL se obtiene aplicando ley de Ohm:
T
1 T
R LI(t)dt = R L é ò I(t)dt ù = R LIdc Þ VLdc = 400 [W] ´ 0,03[A] = 12,0 [V ]
ò
0
ê
0
úû
ë
T
De modo análogo, para la Ief y el VLef se tiene:
VLdc =
Ief =
Vef
20 [V]
Þ Ief =
= 0,033[A]
(RS + RL + 2R f )
(100[W] + 400 [W] + 2 ´ 50[ W] )
VLef = Ief ´ R L = 0,033 [A ] ´ 400 [ W ] Þ VLef = 13,33 [V ]
BRÉGAINS, IGLESIA, LAMAS
(EjsT04. 51)
(EjsT04. 52)
(EjsT04. 53)
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 29 DE 32
b) CORRIENTE I(t) Y TENSIÓN VL(t) SOBRE RL CON DZ: Como Vb>Vc, DZ siempre está en inversa. Entonces:
Cuando Ve-Vh<VZ, DZ OFF:
Cuando Ve-Vh>VZ, DZ Zéner:
Por lo tanto, para la tensión VL(t):
Puntos de interés en la curva: 1 y 2. Se cumple
æ 2p ö
æ 2p ö
VLm sen ç
t ÷ = VZ Þ R LImax sen ç
t ÷ = VZ
è T ø
è T ø
Þ
R L p Idc
æ 2p ö
sen ç
t ÷ = VZ
2
è T ø
Puntos 1 y 2:
ì t1 = 0,11 T
2p
ï
æ 2p ö
18,84 sen ç
t ÷ = 12 Þ
t = arcsen ( 0,6366 ) Þ í
T
T
è
ø
ïî t 2 = 0,39 T
(EjsT04. 56)
Para la corriente I(t):
Valores relevantes de I(t):
VLm 18,84 [ V ]
=
= 0,047[A] = Im ax
RL
400 [ W ]
12 [ V ]
VZ
=
= 0,03[A]
RL 400 [ W ]
(EjsT04. 57)
c) EXPRESIONES DE LAS INTEGRALES PARA OBTENER LAS ENSIONES VLdc Y VLef SOBRE RL:
VLdc =
2
VLef
=
t1
t2
t1
t2
2é
2
2VLm ò sen ( wt ) dt + ò VZ dt ù = é 37,68 ò sen ( wt ) dt + 12ò dt ù
ê
0
t
ú
ê
0
t
ë
1
û
ë
1
ûú
T
T
t2
2 é 2 t1
2VLm ò sen2 ( wt ) dt + VZ2 ò dt ù =
0
t
ê
úû
1
Të
EJEMPLOS RESUELTOS DE TE
2é
2 t1
2 t2
2 (18,84 ) ò sen 2 ( wt ) dt + (12 ) ò dt ù
0
t1
ê
úû
Të
(EjsT04. 60)
(EjsT04. 61)
BRÉGAINS, IGLESIA, LAMAS
PÁG. 30 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
APÉNDICE.
POTENCIA A TRAVÉS DE UNA RESISTENCIA.
Si una corriente I(t) = Im sen(wt) pasa por una resistencia R, la POTENCIA INSTANTÁNEA (valor medido en el
instante t) pR(t) disipada en dicha resistencia se obtiene aplicando la Ley de Joule (es la misma I2R que se
aplica en corriente continua, pero adaptada a una corriente variable en el tiempo):
é
2
æ 2p
pR (t ) = [I ( t )] R = êI m sen ç
èT
ë
2
öù
t ÷ú R
øû
(ApIPCA. 1)
En corriente alterna, como las corrientes y los voltajes están variando periódicamente en el tiempo, resulta
más útil hablar de VALORES PROMEDIO que de valores instantáneos. Las funciones se repiten en cada periodo
T, de modo que los valores promedio se calculan en ese lapso (es decir, entre t = 0 y t = T), ya que eso es
suficiente para saber cómo serán los promedios en los periodos posteriores. Bajo esta perspectiva,
podemos calcular la potencia promedio disipada por la resistencia R. Para ello primero debemos definir el
concepto de valor promedio (en el tiempo) de una función periódica.
Recuerda: cuando los potenciales y las corrientes varían periódicamente en el tiempo, hay dos conceptos:
·
·
Valor INSTANTÁNEO (como potencia en el instante t, por ejemplo).
Valor PROMEDIO (como potencia media, por ejemplo).
VALOR PROMEDIO TEMPORAL DE UNA FUNCIÓN.
Para aclarar la idea de la fórmula utilizada para calcular el valor promedio, empecemos con un ejemplo
sencillo. Supongamos que tienes N tablones (N = 30, por ejemplo, si quieres especificar un valor), cada uno
con la misma anchura Da (por ejemplo 0,1 metros) y grosor, pero de distintas longitudes, y deseas hallar la
longitud promedio. Los dispones en vertical, uno a continuación del otro, como lo indica la FIGURA_API. 1.
Cada uno poseerá una altura (longitud) dada en metros: h1 metros, h2 metros, etcétera, hasta hN.
FIGURA_API. 1
Para hallar el promedio de las alturas hprom, sumas cada una de ellas y divides esa suma por el número de
tablones (esa es la definición de valor promedio):
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
PÁG. 31 DE 32
N
hprom =
h1 + h2 + h3 + ... + hN
=
N
åh
n =1
N
n
(ApIPCA. 2)
[metros]
Ahora haz un truco: multiplica y divide la ecuación anterior por Da (esto no cambiará el resultado):
N
hprom =
Daå hn
n =1
DaN
N
=
å h Da
n =1
n
N Da
=
h1Da + h2 Da + h3 Da + ... + hN Da A
=
N Da
L
[metros]
(ApIPCA. 3)
en donde hemos metido la Da dentro de la suma porque era factor común.
Aplicando ese “truco” observamos que el cálculo de la altura promedio es equivalente a obtener el área total
de los tablones A (suma del área del primer tablón h1.Da, más el área del segundo tablón h2.Da, más el
tercero h3.Da, etcétera) y dividirlo por la longitud total L = NDa de las anchuras. Bien, qué pasa si los
tablones se hacen más y más estrechos (Da®0, la anchura de cada uno tiende a cero), y su número
aumenta indefinidamente (N®¥), manteniendo L constante? Que las alturas hn se transforman en una
función continua de a, es decir hn®h(a), y…
N
hprom = lim
N ®¥
Da ®0
å h Da
n =1
n
N Da
lim
=
N
å h Da
N ®¥
Da ®0 n =1
L
n
a
=
1 N
1
h(a ) da =
ò
L a1
aN - a1
aN
ò h(a) da
[metros]
(ApIPCA. 4)
a1
es decir que la altura promedio se transforma en la integral definida de h(a) entre los extremos a1 y aN,
dividida por la longitudVIII L = aN-a1. O lo que es lo mismo: es el área bajo la curva h(a), es decir la integral
entre los puntos inicial y final del intervalo, dividida la longitud total del intervalo L, exactamente como se ha
dicho anteriormente: sólo hemos pasado de una función discreta (los tablones tienen alturas que van “a
saltos”, como una escalera) a una continua (los saltos de h al pasar de un punto a otro son más suaves).
Con esta última fórmula se observa perfectamente que la integral definida es una suma (de hecho, el
símbolo de la S alargada, ò, se ha inventado para recordar que la integral es una suma).
La ecuación representa la definición de valor promedio de una función. Por ejemplo, si tenemos una función
f que varía con el tiempo t, y queremos hallar el promedio temporal entre los instantes ta y tb, simplemente
cambiamos las variables, pero el significado será el mismo:
t
f prom = Promedio temporal de f (t ) =
1 b
f (t ) dt
t b - ta tòa
(ApIPCA. 5)
En el caso del promedio de una función periódica f(t) de periodo T, el promedio se halla entre ta = 0 y tb = T,
es decir:
fprom =
1 T
f (t ) dt
T ò0
(ApIPCA. 6)
COMO CONCLUSIÓN: para hallar el valor medio de una función periódica f(t) de periodo T, hay que integrar
dicha función entre 0 y T y dividir esa integral por el periodo T.
VIII
Si observas la FIGURA_API. 1, verás que en realidad L = (aN+Da)-a1 , pero como Da®0, entonces la expresión L = aN-a1 es correcta
en la ecuación (ApIPCA. 4).
EJEMPLOS RESUELTOS DE TE
BRÉGAINS, IGLESIA, LAMAS
PÁG. 32 DE 32
EJEMPLOS TEMA 04 (CIRCUITOS CON DIODOS)
VALOR MEDIO DE LA POTENCIA A TRAVÉS DE UNA RESISTENCIA.
Aplicando la definición anterior, queremos hallar el valor promedio de la potencia a través de la resistencia.
Entonces, tenemos que integrar la potencia instantánea pR(t) = I2(t)R en un periodo T. En la ecuación
anterior, simplemente reemplazamos f(t) por pR(t):
{
}
1 T
1 T
2
(ApIPCA. 7)
pR (t ) dt = ò [I (t )] R dt
T ò0
T 0
El resultado de esta ecuación NO depende del instante t, es un número: el promedio de pR(t) en el intervalo
de t=0 a t=T.
pRprom = PR =
Como R = constante, podemos extraerla fuera de la integral:
2
ì1 T
ü
pRprom = PR = R í ò [I (t )] dt ý
0
T
î
þ
(ApIPCA. 8)
Para comparar esta ecuación con la I2R que se utiliza en corriente continua, llamamos a lo que está entre
corchetes corriente eficaz al cuadrado Ief2:
2
ì1 T
ü
pRprom = PR = R í ò [I (t )] dt ý Þ pRprom = PR = Ief2 R
0
T
î144
2443þ
(ApIPCA. 9)
2
=Ief
Aquí se observa perfectamente que la corriente eficaz es la corriente que, elevada al cuadrado y
multiplicada por R, DA EL VALOR DE LA POTENCIA PROMEDIO disipada por la resistencia RIX.
Hallemos el valor eficaz para la función senoidal I(t) = Im sen(wt). Entonces, debemos calcular:
Ief2 =
1 T
T ò0
é
æ 2p
êIm sen ç T
è
ë
2
1 T
öù
æ 2p
t ÷ ú dt = ò Im2 sen2 ç
T 0
øû
èT
ö
t ÷ dt
ø
(ApIPCA. 10)
Esta integral se puede resolver fácilmente, sabiendo que sen2(A)= ½ [1 - cos(2A)]. Así que, haciendo A =
wt, encontramos que sen2(wt) = ½ {1 - cos[2(wt)]}, por lo tanto:
T
Im2 é T
dt - ò cos ( 2w t ) dt ù =
ò
0
0
0
ûú
2T ëê 0
2
2
2
2
2
T
T
I T
I
I
I T
I
é æ 2p ö ù
= m ò dt - m ò cos ( 2w t ) dt = m ò dt - m ò cos ê2 ç
t ÷ ú dt = m T Þ
0
0
0
0
2T
2T
2T { 2T
è T ø û3 2 T
ë 2444
1444
=T
Ief2 =
Im2
T
ò
T
sen 2 ( w t ) dt =
Im2
T
ò
T
½ éë1 - cos ( 2w t ) ùû dt =
(ApIPCA. 11)
=0
Þ Ief2 =
2
m
I
I
I
I
I
Þ Ief =
=
= m ® Ief = m
2
2
2
2
2
2
m
2
m
Hemos hallado el valor eficaz de una corriente sinusoidal. Finalmente:
(
)
2
(
)
PR = Ief2 R = Im / 2 R = Im2 / 2 R
(ApIPCA. 12)
Para otro tipo de funciones no sinusoidales, hay que aplicar la definición análoga a la (ApIPCA. 10).
IX
Podemos dar una idea conceptual más clara. Si por R pasa una corriente continua Icc = constante (donde el subíndice cc indica
2
2
“corriente continua”), entonces PRcc = (Icc) R. Si por R pasa una corriente alterna I(t), entonces PRca = (Ief) R. Queremos ahora que la
potencia promedio disipada por la corriente alterna en R sea igual a potencia disipada por la corriente continua. Entonces hacemos PRca
2
2
= PRcc lo cual implica (Ief) R = (Icc) R Þ Ief = Icc. EN PALABRAS: para que la potencia disipada en una resistencia R por una corriente
alterna I(t) sea igual a la potencia disipada por una corriente continua Icc, la corriente eficaz Ief tiene que tener el mismo valor que la Icc.
BRÉGAINS, IGLESIA, LAMAS
TECNOLOGÍA ELECTRÓNICA, CURSO 2009/2010