CostosIndustriales2 File - FACETVirtual
Anuncio

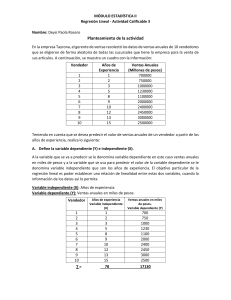
Especialización Gestión Industrial COSTOS INDUSTRIALES Marcelo Medina Funciones de Costos Objeto de Costo Todo aquello para lo que se desea una medida separada de costos Causante de Costo Cualquier elemento o variable que afecta los costos Función de Costo Patrón de comportamiento de los costos Funciones de Costos Supuesto 1 Nivel de Actividad Supuesto 2 Aproximación Lineal Costo Variable Costo Fijo Costo Mixto Los administradores necesitan: Estimar Costos Predecir Costos Favorecer la Planeación y TTDD Funciones de Costos Criterio de Causa - Efecto Relaciones Físicas Acuerdos Contractuales Conocimiento de las Operaciones Métodos de Medición de Funciones de Costos Análisis de Ingeniería Análisis de Consenso Análisis de Cuentas Análisis Cuantitativo Método Máximo-Mínimo Método de Regresión Lineal • Simple • Múltiple Calculo de una función de costos 1. Seleccionar la variable dependiente 2. Identificar los factores de costos 3. Recopilación de los datos 4. Presentar los datos en forma gráfica 5. Estimar la Función de costos 6. Evaluar la Función de costos FUNCIONES DE COSTOS Variable dependiente Variables independientes y f x 1 ; x 2 ;...; x n Nombre de la función N° entero >0 AJUSTE LINEAL DE LA FUNCIÓN DEL COSTO En este punto asumiremos los supuestos siguientes: 1. Que el costo total en el corto plazo puede expresarse correctamente como una función CT, la cual es LINEAL simple o lineal múltiple. 2. La función CT es igual a la suma de una función CF constante correspondiente al costo fijo total, y una función CVT correspondiente al costo variable total. 3. CVT es la suma de una o más funciones lineales simples, cada una de las cuales es dependiente de un factor de costos fácilmente identificable como el número de unidades producidas, la cantidad de mano de obra directa empleada, el volumen de producción, etc. 4. Si conjuntamente con el costo fijo total, existen costos SEMIVARIABLES, entonces estos son susceptibles de ser segmentados o divididos a su vez en costos fijos y en costos variables. CT CF CVT MÉTODOS PARA SEGMENTAR COSTOS y a bx (3.1) X 2 Y X XY a n X 2 X 2 Variable y = Dependiente a = Constante b = Constante x = Independiente y a b 1x 1 b 2 x 2 .. b n x n (3.3) b Representa (3.2) n XY X Y n X 2 X 2 Siglas Costo total CT Costo fijo CF Costo variable unitario CVu Número de unidades producidas Q (3.4) PROCEDIMIENTO Calcular los coeficientes a y b con las fórmulas. Estos datos bajo los supuestos de que no existen cambios sustanciales con los datos históricos proporcionarán el CF y el CVu respectivamente. Recuerde que a no es el costo esperado de la actividad cero. Hallar R2 que indica la bondad del ajuste, que va desde 0 hasta 1. Es una medida intuitiva del grado en que la variable independiente explica la variable dependiente. Un análisis de regresión debe ser factible económicamente, tener un adecuado R2, el coeficiente b debe ser bastante diferente de cero, complementado con un análisis de especificación (linealidad, variación constante, independencia y normalidad de los residuales)