Sesion N°4_Folleto con actividades_Actualizado al 27 junio

Reiman Acuña
Jorge Chinchilla
Escuela de Matemática
Instituto Tecnológico de Costa Rica
Estadística y Probabilidad
para profesores de matemática
2015
Reiman Y. Acuña & Jorge L. Chinchilla.
Compilación
Probabilidad
para profesores de matemática
Alajuela, 27 de junio del 2016
Índice general
1
Estadística . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.1
Introducción
5
1.2
Histórica de la Estadística
5
1.3
Medidas de Tendencia Central
1.3.1
1.3.2
1.3.3
1.3.4
1.3.5
1.3.6
La media . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Media ponderada . . . . . . . . . . . . . . . . . . . . . . . . . . . .
La media para frecuencias simples . . . . . . . . . . . . . . .
La mediana . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
La moda . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Media, mediana y moda de subgrupos combinados
1.4
Comparación de las Medidas de Tendencia Central
14
1.5
Medidas de variabilidad
18
1.5.1
1.5.2
1.5.3
Recorrido o amplitud . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Desviación estándar y varianza . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
Coeficiente de variación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2
Probabilidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
2.1
La enseñanza de la probabilidad en secundaria
2.1.1
Historia de la Probabilidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.2
Conceptos básicos de probabilidad
2.2.1
2.2.2
Experiencias Aleatorias . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Espacio muestral y eventos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.2.3
Álgebra de eventos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
8
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. 9
. 9
10
11
12
13
27
29
2.3
Probabilidad
2.3.1
2.3.2
2.3.3
2.3.4
2.3.5
2.3.6
2.3.7
2.3.8
2.3.9
2.3.10
Función de probabilidad . . . . . . . . . . . . . . .
Espacio probabilizable o σ −algebra . . . . .
Regla de la suma . . . . . . . . . . . . . . . . . . . . .
Propiedades de la probabilidad . . . . . . . . .
Regla de multiplicación de probabilidades
Probabilidad condicionada . . . . . . . . . . . .
Teorema de la probabilidad total . . . . . . . .
Sucesos independientes . . . . . . . . . . . . . . .
La ley de los grandes números . . . . . . . . . .
Teorema del Límite Central . . . . . . . . . . . . .
Bibliografía
34
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
37
37
38
38
40
41
44
46
50
50
51
1 — Estadística
1.1
Introducción
Actualmente la Estadística es la ciencia que proporciona instrumentos e ideas que permiten utilizar
los datos obtenidos por algún medio para profundizar en la comprensión de distintos temas. Pero
etimológicamente la Estadística es la ?Ciencia del Estado?, porque desde la antigüedad los Estados
han recogido datos sobre sus habitantes con los principales objetivos, aunque no únicos, como
veremos, de recaudar impuestos o reclutar jóvenes para el ejército.
Pero además de los signifi cados anteriores, la palabra ?estadística? también puede signifi car una
colección de datos. Así pues, en muchas lenguas se usa la misma palabra para referirnos a la ciencia
que estudia los datos y también para designar a los datos. Estos dos signifi cados se aprecian mejor
si pensamos por un lado en la Estadística y por otro en las estadísticas. Y así, con las dos palabras,
estadísticas y Estadística, llegamos a los dos grandes bloques en que se suele dividir a la Ciencia
Estadística: la Estadística descriptiva y la Estadística inferencial.
La Estadística descriptiva describe, representa y resume situaciones prácticas en las que existe
incertidumbre y que atañen a colectivos con un número importante de individuos. Podrían ser personas, pero también podría tratarse de objetos producidos industrialmente o de resultados de la cosecha.
La Estadística inferencial tiene por objeto obtener conocimiento de la población a partir de observaciones relativas a sólo una parte de ella, lo que se conoce como una muestra de la misma.
1.2
Histórica de la Estadística
Los comienzos de la estadística pueden ser hallados en el antiguo Egipto, cuyos faraones lograron
recopilar, hacia el año 3050 antes de Cristo, datos relativos a la población y la riqueza del país.
6
Estadística
De acuerdo al historiador griego Heródoto, dicho registro se hizo con el objetivo de preparar la
construcción de las pirámides. En el mismo Egipto, Ramsés II hizo un censo de las tierras con el
objeto de verificar un nuevo reparto.
En el antiguo Israel la Biblia da referencias, en el libro de los Números, de los datos estadísticos
obtenidos en dos recuentos de la población hebrea. El rey David por otra parte, ordenó a Joab,
general del ejército hacer un censo de Israel con la finalidad de conocer el número de la población.
También los chinos efectuaron censos hace más de cuarenta siglos. Los griegos efectuaron censos
periódicamente con fines tributarios, sociales (división de tierras) y militares (cálculo de recursos y
hombres disponibles). La investigación histórica revela que se realizaron 69 censos para calcular los
impuestos, determinar los derechos de voto y ponderar la potencia guerrera.
Pero fueron los romanos, maestros de la organización política, quienes mejor supieron emplear los
recursos de la estadística. Cada cinco años realizaban un censo de la población y sus funcionarios
públicos tenían la obligación de anotar nacimientos, defunciones y matrimonios, sin olvidar los
recuentos periódicos del ganado y de las riquezas contenidas en las tierras conquistadas.
Durante los mil años siguientes a la caída del imperio Romano se realizaron muy pocas operaciones
Estadísticas, con la notable excepción de las relaciones de tierras pertenecientes a la Iglesia, compiladas por Pipino el Breve en el 758 y por Carlomagno en el 762 DC. En Inglaterra, Guillermo el
Conquistador recopiló el Domesday Book o libro del Gran Catastro para el año 1086, un documento
de la propiedad, extensión y valor de las tierras de Inglaterra. Esa obra fue el primer compendio
estadístico de Inglaterra.
Durante los siglos XV, XVI, y XVII, hombres como Leonardo de Vinci, Nicolás Copérnico, Galileo,
Neper, William Harvey, Sir Francis Bacon y René Descartes, hicieron grandes operaciones al método
científico, de tal forma que cuando se crearon los Estados Nacionales y surgió como fuerza el
comercio internacional existía ya un método capaz de aplicarse a los datos económicos.
Durante un brote de peste que apareció a fines de la década de 1500, el gobierno inglés comenzó
a publicar estadística semanales de los decesos. Esa costumbre continuó muchos años, y en 1632
estos Bills of Mortality (Cuentas de Mortalidad) contenían los nacimientos y fallecimientos por sexo.
En 1662, el capitán John Graunt usó documentos que abarcaban treinta años y efectuó predicciones
sobre el número de personas que morirían de varias enfermedades y sobre las proporciones de
nacimientos de varones y mujeres que cabría esperar. El trabajo de Graunt, condensado en su obra
Natural and Political Observations...Made upon the Bills of Mortality (Observaciones Políticas y
Naturales ... Hechas a partir de las Cuentas de Mortalidad), fue un esfuerzo innovador en el análisis
estadístico.
Por el año 1540 el alemán Sebastián Muster realizó una compilación estadística de los recursos
nacionales, comprensiva de datos sobre organización política, instrucciones sociales, comercio y
poderío militar. Durante el siglo XVII aportó indicaciones más concretas de métodos de observación
1.2 Histórica de la Estadística
7
y análisis cuantitativo y amplió los campos de la inferencia y la teoría Estadística.
El primer empleo de los datos estadísticos para fines ajenos a la política tuvo lugar en 1691 y estuvo
a cargo de Gaspar Neumann, un profesor alemán que vivía en Breslau. Este investigador se propuso
destruir la antigua creencia popular de que en los años terminados en siete moría más gente que en
los restantes, y para lograrlo hurgó pacientemente en los archivos parroquiales de la ciudad. Después
de revisar miles de partidas de defunción pudo demostrar que en tales años no fallecían más personas
que en los demás. Los procedimientos de Neumann fueron conocidos por el astrónomo inglés Halley,
descubridor del cometa que lleva su nombre, quien los aplicó al estudio de la vida humana. Sus
cálculos sirvieron de base para las tablas de mortalidad que hoy utilizan todas las compañías de
seguros.
Durante el siglo XVII y principios del XVIII, matemáticos como Bernoulli, Francis Maseres, Lagrange y Laplace desarrollaron la teoría de probabilidades. No obstante durante cierto tiempo, la teoría
de las probabilidades limitó su aplicación a los juegos de azar y hasta el siglo XVIII no comenzó a
aplicarse a los grandes problemas científicos.
Godofredo Achenwall, profesor de la Universidad de Gotinga, acuñó en 1760 la palabra estadística,
que extrajo del término italiano statista (estadista). Creía, y con sobrada razón, que los datos de la
nueva ciencia serían el aliado más eficaz del gobernante consciente. La raíz remota de la palabra se
halla, por otra parte, en el término latino status, que significa estado o situación; Esta etimología
aumenta el valor intrínseco de la palabra, por cuanto la estadística revela el sentido cuantitativo de
las más variadas situaciones.
Jacques Quételect es quien aplica las Estadísticas a las ciencias sociales. Este interpretó la teoría de la
probabilidad para su uso en las ciencias sociales y resolver la aplicación del principio de promedios y
de la variabilidad a los fenómenos sociales. Quételect fue el primero en realizar la aplicación práctica
de todo el método Estadístico, entonces conocido, a las diversas ramas de la ciencia.
Entretanto, en el período del 1800 al 1820 se desarrollaron dos conceptos matemáticos fundamentales
para la teoría Estadística; la teoría de los errores de observación, aportada por Laplace y Gauss; y la
teoría de los mínimos cuadrados desarrollada por Laplace, Gauss y Legendre. A finales del siglo
XIX, Sir Francis Gaston ideó el método conocido por Correlación, que tenía por objeto medir la
influencia relativa de los factores sobre las variables. De aquí partió el desarrollo del coeficiente de
correlación creado por Karl Pearson y otros cultivadores de la ciencia biométrica como J. Pease Norton, R. H. Hooker y G. Udny Yule, que efectuaron amplios estudios sobre la medida de las relaciones.
Los progresos más recientes en el campo de la Estadística se refieren al ulterior desarrollo del
cálculo de probabilidades, particularmente en la rama denominada indeterminismo o relatividad, se
ha demostrado que el determinismo fue reconocido en la Física como resultado de las investigaciones
atómicas y que este principio se juzga aplicable tanto a las ciencias sociales como a las físicas.
Estadística
8
1.3
Medidas de Tendencia Central
Las medidas de tendencia central se utilizan con bastante frecuencia para resumir un conjunto de
cantidades o datos numéricos a fin de describir los datos cuantitativos que los forman.
En nuestra vida diaria, constantemente nos encontramos de manera más común con un concepto estadístico, el “promedio” . Continuamente estamos expuestos a reportes de promedios: salario promedio,
nota promedio, peso promedio, hasta gol promedio. Sin embargo el promedio es una idea ambigua.
Cuando se explora un conjunto desordenado de calificaciones de un examen de matemáticas, por
ejemplo, para ver si su calificación es alta o baja o por encima o por debajo del promedio, está
buscando información estadística relevante que le permitirá interpretar y evaluar su desempeño con
más precisión y significado. Las medidas de tendencia central son también frecuentemente usadas
para comparar un grupo de datos con otro, por ejemplo: el promedio de ventas obtenido por un grupo
de vendedores de una zona, comparado con el promedio de ventas otro grupo de vendedores de otra
zona, el promedio de reclamos de clientes de una sucursal, comparado con el promedio de reclamos
de otra sucursal. Otras características generales de las medidas de tendencia central son las siguientes:
Características
1
Permiten apreciar qué tanto se parecen lo grupos entre sí.
2
Son valores que se calculan para un grupo de datos y que se utiliza para describirlos de
alguna manera.
3
Normalmente se desea que el valor sea representativo de todos los valores incluidos en
el grupo.
4
Es el valor más representativo o típico de un grupo de datos, no es el valor más pequeño
o el más grande, sino un valor que está en algún punto intermedio del grupo, más
exactamente, se acerca a estar al centro de todos los valores, por ello se les llama
medidas de tendencia central.
5
Se utilizan como mecanismo para resumir una característica de un grupo de datos en
particular.
6
También para comparar un grupo de datos contra otro.
Sin embargo, una medida de tendencia central o localización media de los conjuntos de datos está
lejos y por mucho del tipo de índice estadístico más ampliamente utilizado.
Las dos medidas de posición más usadas son la media aritmética, o promedio, y la mediana; en menor
medida se usa la moda. Los cálculos se pueden hacer para datos simples, para datos ponderados o
para datos agrupados en clases.
1.3 Medidas de Tendencia Central
1.3.1
9
La media
La media, llamada también media aritmética, es la medida de tendencia central conocida popularmente como “promedio”. Se define como la suma de todos esos valores dividida por el número de
ellos. La media aritmética puede ser simple o ponderada.
Definición 1.1 (Media aritmética simple)
Sean X1 , X2 , X3 , . . . , Xn−1 , Xn los n valores observados para una variable cuantitativa X. Entonces la media aritmética o promedio de la variable X, que se denota con una barra encima de X,
es:
X1 + X2 + X3 + . . . + Xn−1 + Xn
X=
n
En notación de sumatoria, la media aritmética se escribe:
X=
1 n
∑ Xi
n i=1
1.1
Suponga que se tienen las notas obtenidas por un grupo de 20 estudiantes en un examen
universitario y que sus valores (ordenados de menor a mayor) son: 15, 45, 47, 53, 58, 58, 60,
62, 67, 74, 75, 78, 80, 80, 81, 85, 85, 85, 90, 92
Entonces la media es:
X=
15 + 45 + 47 + 53 + 58 + 58 + 60 + · · · + 75 + 78 + 80 + 80 + 81 + 85 + 85 + 85 + 90 + 92
20
es decir,
X=
1370
20
Por lo tanto, la nota promedio es 68,50.
1.3.2
Media ponderada
A veces interesa dar diferentes pesos o ponderaciones a los diferentes valores de la variable, de
acuerdo con su importancia. Ante esto, tenemos la siguiente definición
Definición 1.2 (Media ponderada simple)
Sean X1 , X2 , X3 , . . . , Xn−1 , Xn los n valores observados para una variable cuantitativa X,
donde los datos están ponderados por los p1 , p2 , p3 , . . . , pn , es decir, estos valores pi dan la
importancia relativa que tiene cada unidad estadística en el estudio.
Estadística
10
Entonces la media ponderada de la variable X es :
X=
p1 X1 + p2 X2 + p3 X3 + . . . + pn Xn
p1 + p2 + . . . + pn
En notación de sumatoria, la media ponderada es:
X=
∑ni=1 pi Xi
∑ni=1 pi
1.2
Supóngase que un estudiante tiene las siguientes notas en cuatro cursos matriculados un
cuatrimestre: 67, 82, 90, 71. El número de créditos que vale cada curso es, respectivamente: 3,
2, 2, 4. Entonces la media ponderada de las notas será:
X=
1.3.3
(3 × 67) + (3 × 82) + (2 × 90) + (4 × 71) 829
=
= 75,36
3+2+2+4
11
La media para frecuencias simples
Cuando los datos recolectados han sido organizados en una tabla de distribución de frecuencias
simples, la media, para poblaciones como para muestras, se puede calcular por medio de la fórmula
x=
∑ fx
n
en donde
x = media o promedio
∑ fx
= suma de las frecuencias
por su correspondiente
dato nominal.
n = suma de todas las frecuencias (número de datos recolectados)
Calificaciones
x
0
1
2
3
4
5
6
7
8
9
10
Total
f
2
3
3
6
8
9
17
22
10
6
5
91
1.3 Medidas de Tendencia Central
11
1.3
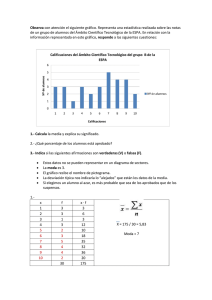
Las calificaciones de Matemáticas de los grupos ”A” y ”B” se muestran en la tabla de la
derecha. Calcular el promedio (la media) obtenido por esos grupos.
Solución: Debe añadirse a la tabla original una columna encabezada por f x en donde se anotarán
los resultados correspondientes a las multiplicaciones de cada valor nominal x por su frecuencia f
respectiva.
Por ejemplo, para la primera fila de la tabla: f x = 2 × 0 = 0
La tabla completa con las tres columnas
queda como se muestra a la derecha. La
suma de los valores de la columna f x es
Calificaciones
544, de manera que utilizando la fórmux
la para el promedio,recordando que n es
0
la suma de todas las f , se obtiene:
1
544
2
x =
91
3
x = 5,97
4
5
6
7
8
9
10
Total
1.3.4
f
2
3
3
6
8
9
17
22
10
6
5
91
fx
0
3
6
18
32
45
102
154
80
54
50
544
La mediana
La mediana es el valor que esta en el “centro” de todos los valores, si éstos se ordenan. Es decir, es
un valor tal que no más de la mitad de las observaciones son mayores que él y que no más de la
mitad son menores que él. La mediana se denota Me. Esto es
Definición 1.3 (Mediana)
Supóngase que se tienen las observaciones X X1 , X2 , X3 , . . . , Xn−1 , Xn de una variable
cuantitativa y que estas observaciones están ordenadas. Entonces el valor de la mediana
dependerá de si el número n de datos es par o impar:
I
Si n es impar, entonces la mediana se encuentra en la posición (n + 1) ÷ 2, que es
exactamente la posición que separa los datos en dos grupos de igual cantidad:
Me =
X(n+1)
2
Estadística
12
II
Si n es par, entonces la mediana estará entre la posición n/2 y la posición n/2 + 1, para
que los datos se dividan en dos grupos de n/2 valores cada uno.
Es usual entonces tomar la mediana como la media aritmética entre los datos Xn /2 +
Xn /2 + 1, es decir:
Me = (Xn /2 + Xn /2 + 1) ÷ 2
(Observe que ambos valores pueden coincidir).
1.4
Supóngase que se tienen los siguientes datos ordenados de una variable cuantitativa:
−3, −3, −2, 0, 0, 1, 3 , 3, 5, 8, 8, 10, 10. Como hay n = 13 datos, que es un número impar,
entonces la mediana está en la posición (n + 1) ÷ 2 = (13 + 1) ÷ 2 = 7 , es decir, que Me = 3.
Esto significa que el 50 % de los datos son mayores o iguales que 3 y el otro 50 % de los datos
on menores que 3. Nótese que a partir de la fórmula se obtiene la posición de la mediana y no
el valor de ésta.
1.5
Consideremos las notas obtenidas por un grupo de 20 estudiantes universitarios:
15, 45, 47, 53, 58, 58, 60, 62, 67, 74 , 75 , 78, 80, 80, 81, 85, 85, 85, 90, 92
Como el número de datos es 20, que es par, entonces la mediana será la media aritmética entre
los datos que están en la posición n/2 = 10 y la posición n/2 + 1 = 11. Estos datos son: 74 y
75. Entonces la mediana es:
Me = (74 + 75) ÷ 2 = 74,5
1.3.5
La moda
La moda es la medida de posición más simple de definir:
Definición 1.4 (Moda)
Dada una serie de observaciones para una variable cuantitativa, entonces la moda, denotada
MO , es el valor más frecuente (si existe), o los valores más frecuentes (si son varios).
Si un grupo de datos presenta una sola moda, diremos que es unimodal. Si presenta dos modas,
diremos que es bimodal.
La moda es la medida de posición que menos se usa por una sencilla razón: en muchas ocasiones no
existe. Peor aún, cuando existe, frecuentemente no es única, sino que existen muchas modas para
una misma serie de datos. Por lo tanto, advertimos al estudiante acerca de su uso y su interpretación.
1.3 Medidas de Tendencia Central
13
1.6
Consideremos de nuevo la siguiente serie de datos, correspondiente a las notas de un grupo de
estudiantes:
15, 45, 47, 53, 58, 58, 60, 62, 67, 74, 75, 78, 80, 80, 81, 85, 85, 85, 90, 92
Entonces la moda es 85, que tiene frecuencia 3. O sea, que la nota más frecuente es 85.
1.7
Supóngase que se tienen observadas las siguientes estaturas de 10 personas, en centímetros:
168, 162, 181, 180, 169, 171, 175, 159, 173, 160
Como no hay ningún valor que sea más frecuente que los demás, entonces la moda no existe.
1.8
En una pequeña empresa familiar, se tienen los siguientes salarios mensuales de los empleados,
en miles de colones:
30, 35, 35, 35, 40, 90, 120, 120, 120, 150
Entonces hay dos modas: 35 y 120, ambas con frecuencia 3.
1.3.6
Media, mediana y moda de subgrupos combinados
Suponga que se conocen la media, la mediana y la moda de calificaciones de examen para cada una
de tres escuelas por separado (subgrupos), pero deseamos encontrar las tres medidas de tendencia
central para el grupo compuesto (es decir, las tres escuelas combinadas en un grupo grande). Dadas
las medidas de los tres subgrupos y sus respectivas n, podemos calcular la media compuesta (llamada
media mayor simbolizada por X. ), mediante la ecuación:
X. =
N
∑ X1 + ∑ X2 + . . . + ∑ X j
n1 + n2 + . . . n j
Advertencia:
A La media mayor no sólo es la media de las medias de los subgrupos a menos que los
tamaños de las muestras de los subgrupos sean idénticas. La media mayor (X) de grupos
medida diferente se calcula dividiendo la suma de las sumas de los subgrupos entre la
suma de las n del grupo, como esta implícito en la ecuación anterior.
B Las modas o medianas del conjunto de datos compuesto no puede calcularse a partir de
las modas o medianas de los subgrupos. Para la moda y mediana , debemos tener los
datos originales a la mano y formar una distribución de frecuencias combinada simple
antes de que la moda o la mediana de los datos agregados pueda encontrarse.
Estadística
14
C
Con muestras de subgrupos pequeños, la media, moda y mediana del grupo compuesto
son simples de determinar. Si embargo, en el caso de conjuntos grandes de datos que
están involucrados, solo la media mayor es razonablemente simple de calcular. Sólo la
media se define algebraicamente por la ecuación
X = ∑ X/n
.
1.4
Comparación de las Medidas de Tendencia Central
El propósito de las medidas de posición ( tendencia central) es resumir o representar un conjunto
de datos. Dichas medidas se complementan y en conjunto, permiten una mejor descripción de las
características de la distribución de los datos. El problema reside en escoger cuál de las medidas
representa mejor dicho conjunto de datos, para ello es necesario tener una idea acerca de la forma de
su distribución.
Las ventajas y limitaciones de usar la media, la moda y la mediana para describir un conjunto de
datos depende estrictamente de la forma (tipo) de la distribución de datos. Siempre que se pueda usar,
en general se prefiere la media para describir la tendencia central, aunque algunas distribuciones se
describen mejor por medio de la moda y la mediana. A continuación evaluaremos la aplicabilidad de
nuestros tres “promedios” a diferentes tipos de distribuciones.
Comparaciones
1
En una distribución normal (simétrica), la media, moda y mediana tienen un valor
idéntico (Figura 1). Esto en realidad es evidente, dado que una distribución normal es
perfectamente simétrica, y la curva tiene un sólo punto máximo (moda) que también se
encuentra en el centro. Así, la media debe ser nuestra medida preferida de tendencia
central para los conjuntos de datos que se distribuyen normalmente, puesto que es más
fácil de calcular y de usar en forma matemática.
Figura 1
2
Una distribución bimodal tiene dos puntos máximos (Figura 2). Esto hace que la media
1.4 Comparación de las Medidas de Tendencia Central
y la mediana no sean de utilidad, puesto que sus valores estarán en algún lugar entre los
dos puntos máximos y distorsionarán enormemente la descripción de la distribución.
La moda, y observe que en este caso hay dos modas, pasa a ser la única medida útil
de tendencia central. Sin embargo, una distribución bimodal es poco común y en
general podemos decir que consta de dos distribuciones que se pueden analizar en
forma independiente.
3
Si hay mucha asimetría, se debe evitar usar la media, ya que ésta es muy sensible a la presencia de valores extremos.
Cuando se describen distribuciones asimétricas (sesgadas) positivas o negativas, la
media no es la mejor medida de tendencia central disponible. Mientras mayor sea la
asimetría o sesgo de los datos, mayor utilidad tendrá la mediana (y más engañosa
será la media), porque la mediana estará más cerca del “valor promedio” real de las
observaciones. Por ejemplo, en el caso de una distribución asimétrica positiva, la media
se encuentra “inflada” por la minoría de las observaciones que tienen un valor mayor.
Esto sucede, por ejemplo, con el ingreso percápita, puesto que las distribuciones del
ingreso son asimétricas positivas. En las siguientes figuras se muestran las posiciones
relativas de la media, la moda y la mediana en cuatro distribuciones asimétricas.
Figura 2
Observe que cuando la distribución es asimétrica “positiva”, (es decir, el extremo más
largo de la distribución apunta hacia el este o hacia su derecha), la moda está a la
izquierda de la mediana, y a su vez, la mediana está a la izquierda del promedio. Sucede
15
Estadística
16
lo contrario cuando la distribución es asimétrica negativa o sesgada negativamente.
Esto nos lleva a una consideración final: si una distribución es asimétrica, es decir,
notoriamente sesgada, la mediana será mejor que la media (promedio aritmético)
para describir la tendencia central de la distribución de los datos. Observe las figuras
anteriores. Note que en todas las distribuciones asimétricas, la mediana efectivamente
se acerca más que la media al valor “promedio” o “normal” de las observaciones o, en
otras palabras, refleja mejor la existencia de un sesgo en los datos.
Para elegir una medida de posición en un grupo de datos, las siguientes consideraciones pueden ser
de utilidad:
Consideraciones
1
La media de un conjunto de datos es la medida que conlleva mayores cálculos
aritméticos y su valor está afectado por los valores individuales de todos los datos,
mientras que la mediana y la moda pueden no ser afectadas por todos los valores. Por
ejemplo, véase el siguiente conjunto de datos, en el que el último valor es aumentado:
Datos
1, 2, 4, 4, 4, 6, 7, 8
1, 2, 4, 4, 4, 6, 7, 26
Media
36 ÷ 8 = 4,5
54 ÷ 8 = 6,75
Mediana
4
4
Moda
4
4
Puede observarse que la media cambia (es sensible al valor extremo 26), mientras que
la moda y la mediana permanecen iguales.
2
En grupos pequeños, la moda puede ser muy inestable o puede no existir.
3
La mediana no se afecta por el tamaño de los valores por encima o por debajo de ella.
4
La media es influida por el tamaño de cada valor en el grupo de datos.
5
Algunos grupos de datos simplemente no manifiestan una posición en forma
significativa, siendo en este caso engañoso calcular una medida de posición.
6
La posición de grupos de datos con valores extremos se mide probablemente mejor por
la mediana, si las observaciones son unimodales. Sin embargo, si lo que se quiere es que
la medida utilizada refleje el efecto de los valores extremos, entonces es conveniente
utilizar la media.
7
La media aritmética es muy útil para estimar la suma total de las observaciones si se
conoce el número de observaciones.
1.4 Comparación de las Medidas de Tendencia Central
17
Ejercicios 1.1
1.1 Los 16 ejecutivos de una empresa ganaron los siguientes salarios para un mes determina-
do:
170000
205000
190000
170000
215000
200000
170000
250000
300000
170000
250000
300000
185000
280000
190000
280000
a.) Calcule la media, la mediana y la moda e interprételas desde el punto de vista del
problema
b.) ¿Qué tipo de asimetría tiene la distribución? ¿Por qué?
1.2 En un curso se han hecho 6 exámenes cortos (quices), y tres estudiantes obtuvieron las
siguientes notas:
Estudiantes
A
B
C
90
77
88
85
78
72
Notas
83 12
82 83
10 90
75
77
72
90
85
85
a.) Calcule todas las medidas de posición.
b.) Si usted fuera el estudiante A, ¿qué medida de posición escogería para tener la nota
máxima?
c.) Si usted fuera el estudiante B, ¿qué medida de posición escogería?
d.) Si usted fuera el estudiante C, ¿qué medida de posición escogería?
1.3 Repecto a los siguientes datos, que corresponden al tiempo, en minutos, redondeado a la
unidad inferior, que duran 30 empleados para ensamblar ciertas piezas:
10
15
12
14
18
10
15
9
17
13
14
16
17
14
12
16
9
11
12
15
16
14
11
12
11
13
14
13
11
15
a.) Construya una distribución de frecuencias completa usando 5 clases, tal que la primera
clase tenga límite inferior 9
b.) ¿Qué porcentaje de empleados duran menos de 15 minutos?
c.) Construya el histograma correspondiente a la distribución de frecuencias
d.) Calcule la media, la mediana, la moda, la desviación estándar y la varianza
1.4 Considere la siguiente tabla de frecuencias que muestra el tiempo que se requiere para
pocesar órdenes de alimentos en un restaurante
Tempo (minutos)
5 a menos de 8
8 a menos de 11
11 a menos de 14
14 a menos de 17
17 a menos de 20
Número de órdenes
10
17
12
6
2
Estadística
18
a.) ¿Qué porcentaje de órdenes se procesan en menos de 14 minutos?
b.) Construya el polígono de frecuancias acumuladas “menos de”.
c.) Calcule la media, la mediana, la moda, la desviación estándar y la varianza
1.5
Medidas de variabilidad
En el apartado anterior se estudiaron las medidas de tendencia central, que son un indicador de
cómo los datos se agrupan o concentran en una parte central del conjunto. Sin embargo, para una
información completa de dicho conjunto de datos hace falta saber el comportamiento opuesto, es
decir, de qué manera se dispersan o se alejan algunos datos de esa parte central. Para tener una idea
de ello, es necesario medir el grado de variabilidad o dispersión de los datos.
Las medidas de variabilidad, también llamadas medidas de dispersión, miden qué tan concentrados
está los datos de una variable cuantitativa alrededor de la medida de posición. Es decir, la variabilidad
o dispersión nos indica si esas puntuaciones o valores están próximas entre sí o si por el contrario
están o muy dispersas.
Si el valor de la medida de variabilidad es pequeño, entonces los datos se parecen mucho entre sí. En
el caso contrario, hay muchos datos diferentes o están muy dispersos.
Hay varias razones para analizar la variabilidad en una serie de datos. Primero, al aplicar una
medida de variabilidad podemos evaluar la medida de tendencia central utilizada. Una medida de
variabilidad pequeña indica que los datos están agrupados muy cerca, digamos, de la media. La
media, por lo tanto es considerada bastante representativa de la serie de datos. Inversamente, una
gran medida de variabilidad indica que la media no es muy representativa de los datos.
Una segunda razón para estudiar la variabilidad de una serie de datos es para comparar como están
esparcidos los datos en dos o más distribuciones.
Por ejemplo, al tomar las temperaturas en una región “A” durante diferentes épocas del año y a
distintas horas del día, se registraron los datos que se muestran en la columna “A” ; por su parte, las
de otra región diferente “B”, son las de la columna “B” .
1.5 Medidas de variabilidad
19
Promedio
A
19,3◦
20◦
20,2◦
20,4◦
21◦
21,3◦
21,3◦
22◦
20,68◦
B
−3◦
0◦
6◦
22◦
31,5◦
34◦
36◦
39◦
20,68◦
Al obtener la media, en ambos casos resultó que la temperatura promedio fue de 20,68, cuya interpretación podría ser que en torno, al rededor o cerca a 20,68 fluctúan los demás valores.
Como puede verse, eso es bastante aproximado para los datos de la columna “A”, no así para los de
la “B”. Los datos más alejados en “A” son 19.3º y 22º, que realmente están próximos a 20.68º; en
cambio, los datos más alejados en “B” son -3º y 39º, que están muy distantes del promedio.
¿Por qué si en ambos casos se tiene igual promedio, no se puede afirmar lo mismo de los valores que
están a su alrededor?. La respuesta está en que no se ha tomado en cuenta la dispersión, es decir, la
manera en que se disgregan los datos respecto de la media, pues en “A” casi no se dispersan mientras
que en “B” sí, .Cabría decir que el conjunto de datos “A” es bastante compacto mientras que el “B”
es muy dilatado.
Las medidas de variabilidad más usadas son la amplitud o recorrido, la desviación estándar, la
varianza y el coeficiente de variación. Al igual que las medidas de posición pueden calcularse para
datos simples o datos agrupados en clases.
1.5.1
Recorrido o amplitud
Definición 1.5 (Recorrido o Amplitud)
El recorrido o amplitud de una serie de datos es la diferencia entre el valor máximo (M) y el
valor mínimo (m) de esa serie. También se conoce como rango y se denota como A.
Luego,
A = M−m
Cuanto mayor sea la amplitud, mayor será la dispersión de los datos de una distribución. A pesar
de lo simple de su cálculo, el recorrido no es muy usado debido a que presenta la dificultad de que
su valor depende de los valores extremos del conjunto de observaciones a que se refiere. En efecto,
como sólo se utilizan dos observaciones para su cálculo, puede suceder que todos los valores de
las observaciones sean muy homogéneos, excepto los dos extremos, el mayor y el menor, que son
precisamente los dos casos que se usan para calcular el recorrido. Por otra parte, la introducción
de nuevas observaciones puede afectar su valor ya que entre las nuevas observaciones puede haber
valores mayores que M o valores menores que m, por lo que el valor de A se aumentaría.
Estadística
20
En los casos de las temperaturas del ejemplo anterior, el rango de “A” esR = 22 − 19,3 = 2,7, en
cambio, el de “B” es B = 39 − (−3) = 42.
1.5.2
Desviación estándar y varianza
Definición 1.6 (Desviación Estándar)
La desviación estándar es el promedio de desviación o diferencia de las observaciones con
respecto a la media aritmética. Se denota como s. Cuanto mayor es la dispersión de los datos
alrededor de la media aritmética, mayor es la desviación estándar.
La desviación estándar es:
r
s=
∑ni=1 (Xi − X)2
n−1
donde : Xi son los datos
X es la media
n número total de datos
la fórmula anterior se puede simplificar como:
s
1 n 2
n
s=
Xi −
(X)2
∑
n − 1 i=1
n−1
Definición 1.7 (Varianza)
La varianza es una medida muy importante para la inferencia estadística, es el cuadrado de la
desviación estándar y se denota s2 . O, lo que es lo mismo, la desviación estándar es la raíz
cuadrada positiva de la varianza.
1.9
Consideremos el ejemplo de las notas obtenidas por un grupo de 20 estudiantes en un examen
universitario:
15, 45, 47, 53, 58, 58, 60, 62, 67, 74, 75, 78, 80, 80, 81, 85, 85, 85, 90, 92
Teníamos que la media de estos datos es 68,50. Para calcular la varianza, primero calculamos
la suma de los cuadrados de los datos:
20
∑ = 152 + 452 + 472 + . . . + 902 + 922 = 100714
i=1
1.5 Medidas de variabilidad
21
Entonces la varianza (de la muestra) es:
s2 =
100714 20
− (68,5)2 = 361,53
19
19
Luego, la desviación estándar (de la muestra) es:
p
s = 361,53 = 19,01
La desviación estándar se interpreta como “cuánto se desvía -en promedio- con respecto a la media
aritmética, un conjunto de observaciones”. En el ejemplo, las notas de los estudiantes se desvían
-en promedio-en 19.01 puntos con respecto a la media aritmética. El lector debe observar que
las unidades de medida de la varianza son el cuadrado de las unidades de medida de la variable
observada, por lo que su interpretación práctica debe ser cuidadosa. Para una comparación con la
media o con los datos, debe usarse la desviación estándar.
1.10
Tú y tus amigos han medido las alturas de tus perros (en milímetros):
Figura 3
Las alturas (de los hombros) son: 600mm, 470mm, 170mm, 430mm y 300mm.
Calcula la media, la varianza y la desviación estándar.
X=
600 + 470 + 170 + 430 + 300
= 394
5
así que la altura media es 394 mm. Vamos a dibujar esto en el gráfico:
Figura 4
Estadística
22
Ahora calculamos la diferencia de cada altura con la media:
Figura 5
Para calcular la varianza:
s2 =
(206)2 + (76)2 + (−224)2 + 362 + (−94)2
= 27130
4
Así que la varianza es 21 130.
Y la√
desviación estándar es la raíz de la varianza, así que:
s = 21130 = 145,36 ahora veremos qué alturas están a distancia menos de la desviación
estándar (145mm) de la media:
Figura 6
Así que usando la desviación estándar tenemos una manera “estándar” de saber qué es normal,
o extra grande o extra pequeño.
Los Rottweilers son perros grandes. Y los Dachsunds son un poco menudos...
Nota: ¿por qué al cuadrado?
Elevar cada diferencia al cuadrado hace que todos los números sean positivos (para evitar que
los números negativos reduzcan la varianza)
1.5.3
Coeficiente de variación
Las medidas de variabilidad que se han mencionado están afectadas por la unidad de medida en
que se expresa la variable. Con frecuencia interesa comparar dos o más series de observaciones en
1.5 Medidas de variabilidad
23
cuanto a su dispersión y para ello se requiere eliminar el efecto de las unidades de medida y de la
magnitud general de los datos que se consideran.
Definición 1.8
El coeficiente de variación mide la variabilidad porcentual o relativa de un conjunto de datos
respecto a su media. Se denota CV :
CV =
s
× 100
X
El coeficiente de variación sirve para comparar la variabilidad de diferentes conjuntos de datos, y es
particularmente útil cuando:
Utilidad
1
Los datos están en unidades diferentes.
2
Los datos están en las mismas unidades, pero las medias son muy diferentes.
1.11
Dos empresas de la industria electrónica, A y B, tienen en el mercado de valores acciones
comunes. El precio medio de cierre en el mercado de valores durante un mes fue, para la acción
A, de ¢15000, con desviación estándar de ¢500. Para la acción B, el precio medio fue de ¢5000,
con desviación estándar de ¢300. Haciendo una comparación absoluta, resultó ser superior
la variabilidad en el precio de la acción A debido a que muestra una mayor desviación estándar.
Pero, con respecto al nivel de precios, deben compararse los respectivos coeficientes de
variación:
sA
CV (A) =
× 100 = (500/15000) × 100 = 3 %
XA
sB
CV (B) =
× 100 = (300/5000) × 100 = 6 %
XB
Por ello, puede concluirse que el precio de la acción B ha sido casi 2 veces más variable que
el precio de la acción A (con respecto al precio medio para cada una de las dos acciones).
Ejercicios 1.2
1.5 Calcule la desviación estándar para los datos que se refieren a los salarios de 16 ejecutivos
de una empresa del ejemplo ya realizado.
1.6 Considere las notas de tres estudiantes del ejercicio visto en este documento. ¿De cuál
de los tres estudiantes podría decirse que tuvo notas más homogéneas?
Estadística
24
1.7 En una empresa, una muestra de 20 trabajadores calificados tienen un salario mensual
medio de ¢55000, con una desviación estándar de ¢67970. En la misma empresa, el salario
mensual medio de una muestra de supervisores es de ¢146150, con una desviación estándar
de ¢91040. Compare la variabilidad de los salarios de los trabajadores de la empresa.
1.8 Tras encuestar a 25 familias sobre el número de hijos que tenían, se obtuvieron los
siguientes datos
Número de hijos
Número de familias
0
5
1
6
2
8
3
4
4
2
Calcular la media, la varianza, la desviación típica y el coeficiente de variación de Pearson.
1.9 Un fabricante de neumáticos ha recabado, de los diferentes concesionarios, información
sobre la cantidad de miles de kilómetros recorridos por un modelo concreto de esos neumáticos
hasta que se ha producido un pinchazo o un reventón del neumático. Los concesionarios la
han proporcionado los siguientes datos:
a.) Construir una taba de frecuencias para esos datos tomando como número de intervalos
el que proporciona la fórmula de Sturgessa . Interpretas la tabla.
b.) Construir las tablas de frecuencias acumuladas ascendente y descendente.
c.) Dibujar el histograma de frecuencias relativas sin acumular y acumulado.
d.) Calcular las principales medidas de tendencia central e interpretarlas.
e.) Obtener las medidas de dispersión más importantes e interpretarlas.
f.) Analizar la asimetría y el apuntamiento de la distribución de frecuencias resultante.
g.) Si el fabricante quiere proponer un kilometraje para realizar el cambio de neumáticos,
1.5 Medidas de variabilidad
¿qué valor propondría para que solo 3 de cada 10 coches hayan tenido un pinchazo o
reventón antes de ese kilometraje?
a La fórmula de Sturgess propone como número k de intervalos, para agrupar un conjunto de N observaciones
en intervalos por k = 1 + [3,3 · log N] En este caso N = 100, luego k = 7. Al ser el valor mínimo 4.3068 se propone
4 como límite inferior del primer intervalo, y al ser 7 intervalos se propone como anchura 13 para cada uno de
ellos, para que sea un valor entero, con lo cual el límite superior del último intervalo es 95
25
2 — Probabilidad
2.1
La enseñanza de la probabilidad en secundaria
De acuerdo con el enfoque propuesto por el Ministerio de Educación Pública, se enfatiza la enseñanza basada en la experimentación y desarrollo de temas con fuerte apego a la contextualización
del educando, por lo que la labor del docente no debe ser vista como el de “resolver” todos los
problemas y ejercicios planteados en el salón de clase.
De acuerdo con Batanero(2013), la enseñanza de la probabilidad en el nivel no universitario debe de
estar marcado bajo una metodología experimental, en donde se plantea a los estudiantes situaciones
probabilísticas bajo contextos prácticos y cercanos a su entorno. Se espera que ellos anoten lo que
sucede a medida que realizan la actividad e ir descubriendo progresivamente que puede saberse
“cuando un suceso es más probable” y “cuánto más probable es”.
Esta autora señala que no debe abordarse el conocimiento de las fórmulas, ni que los estudiantes
realicen cálculos probabilísticos desvinculados de la realidad, al contrario, se busca que ellos exploren sucesos y situaciones acordes a su entorno.
La propuesta del Ministerio de Educación procura que los estudiantes logren mediante actividades
concretas alcanzar ciertas nociones básicas de probabilidad, mediante orientaciones y actividades
sobre su utilidad en diversos contextos (no sólo juegos de azar), posibilitando el desarrollo de
problemas interesantes respecto a la toma de decisión y previsión, relacionados con problemas a los
que tendrán que enfrentarse a lo largo de la vida.
En este sentido, Batanero(2013) nos recuerda tener presente que el azar está en la vida cotidiana
de muchos contextos en los que aparecen nociones de incertidumbre, riesgo y probabilidad. Hay
situaciones en la vida diaria en las que no podemos saber qué resultado va a salir, pero sí sabemos
los posibles resultados; son situaciones que dependen del azar.
Probabilidad
28
Al lanzar una moneda al aire no sabemos si saldrá escudo o corona, pero sí conocemos los posibles
resultados. Cuando lanzamos un dado no sabemos el número que saldrá, pero sabemos que hay seis
posibles resultados. El próximo partido de la Selección Nacional, no sabemos el marcador, pero sabemos que hay tres posibles resultados, así como el pronóstico del tiempo, diagnóstico médico, estudio
de la posibilidad de tomar un seguro de vida o efectuar una inversión, evaluación de un estudiante, etc.
Así pues, consideramos importante que antes de iniciar este tema en nuestros salones de clase en
los distintos colegios del país, es necesario dedicar un tiempo a investigar aspectos relacionados
con el tema en estudio, que puedan resultar motivadores tanto para nosotros mismos como para los
alumnos, de manera que logremos desarrollar el interés y la predisposición a la exploración en el
tema de probabilidad.
Sin embargo, debemos señalar que la Probabilidad por su parte, además de ser una disciplina íntimamente ligada a la Estadística ya que justifica su desarrollo formal y ha aumentado el alcance de sus
aplicaciones, tiene la enorme cualidad, en sí misma, de ser capaz de representar adecuadamente la
realidad de muchos procesos sociales y naturales. Su conocimiento es fundamental para la formación
de un individuo capaz de comprender el mundo en que vivimos.
A continuación algunos aspectos importantes.....
2.1.1
Historia de la Probabilidad
El azar es inherente a nuestras vidas. Se nos presenta de distintas formas en múltiples
situaciones cotidianas que exigen ser resueltas, recurriendo generalmente a la intuición.
Pero las intuiciones en probabilidad con frecuencia nos engañan y una enseñanza
formal es insuficiente para superar los sesgos de razonamiento que pueden llevar a
decisiones incorrectas (Batanero, 2006)
La idea de probabilidad surgió con los juegos de azar, como cartas, lanzamiento de dados, etc.
Cuando la humanidad se enfrentaba a fenómenos para los que no se conocía su causa, como los
asociados al clima, lluvias, tormentas, etc., o a la vida, como el sexo del bebé que va a nacer, las
enfermedades, etc., se atribuían éstos a la voluntad de los dioses. Tal vez por ello los juegos de
azar estuvieron prohibidos en muchas culturas antiguas. En el Renacimiento italiano del siglo XV,
algunos científicos como Galileo (1564-1642) observaron que se producían regularidades en los
resultados de repetir muchas veces el lanzamiento de dados.
Gerolamo Cardano (1501-1576) escribió el primer libro sobre la teoría del azar. Se titulaba El libro
sobre los juegos de azar. La percepción de Cardano sobre como trabaja el azar la expresó en el
concepto de ?espacio muestral?. En ella se basó la descripción matemática de la incertidumbre en
los siglos posteriores.
Hasta el siglo XVII, hacia el 1651, no se realizó el estudio sistemático de un juego de azar. Lo
realizaron Pascal (1623-1662) y Fermat (1601-1675) en Francia. Aunque los juegos de azar estaban
2.2 Conceptos básicos de probabilidad
29
prohibidos en esa época, se practicaban bastante. El Caballero de Meré, amigo de Pascal y jugador
asiduo, preguntó a Pascal la razón por la que al lanzar dos dados ciertas sumas salían con más
frecuencia que otras. Pascal y Fermat desarrollaron un método para calcular las probabilidades
de las apuestas en los juegos de azar. Aunque estos estudios no parecían estar relacionados con
los conocimientos matemáticos de esa época, ambos estaban convencidos de que llegarían a ser
importantes en la ciencia que estudiara los fenómenos aleatorios. En los siglos XVIII y XIX los
científicos se dieron cuenta que se podían estudiar los fenómenos aleatorios con los mismos métodos
que se empleaban para estudiar los juegos de azar. Pero el avance más importante de la Estadística se
debió a la necesidad de estimar cantidades desconocidas en la población a partir de los datos de las
muestras. Este problema llevó a Gauss (1777-1855) a introducir la ?distribución normal? que usaría
Quetelet (1796-1874) para estimar las características medias de los miembros de una comunidad.
En Inglaterra, a finales del siglo XIX, Francis Galton (1822-1911), primo segundo de Darwin, y
Karl Pearson (1857-1936) inventaron métodos para medir relaciones entre diversas variables e
introdujeron la idea de regresión y de coeficiente de correlación. Desde mediados del siglo XIX, el
desarrollo de la teoría de la probabilidad está muy relacionada, y en deuda, con los descubrimientos
de científicos rusos, entre los que destacan Chevichev, Markov, Lyapunov y Bunyakovsky. Chevichev
introdujo la ley de los grandes números que dice que cuando un experimento se realiza un número
grande de veces, la frecuencia relativa tiende a la probabilidad del mismo.
Markov introdujo las cadenas de su nombre, que son series de eventos en los que la probabilidad
de que ocurra un evento depende del resultado del evento anterior. Lyapunov descubrió el teorema
central del límite que expresa que para cualquier población (aunque no se distribuya normalmente) la
distribución muestral de la media tiende a distribuirse normalmente cuando el tamaño de la muestra
es suficientemente grande. Bunyakovsky desarrolló aplicaciones de la teoría de la probabilidad a la
Estadística, en particular en el campo de los seguros y en la demografía. Escribió el primer curso
ruso sobre probabilidad.
2.2
Conceptos básicos de probabilidad
Hay situaciones en la vida diaria en las que no podemos saber qué resultado va a salir, pero sí
sabemos los posibles resultados; son situaciones que dependen del azar.
Al lanzar una moneda al aire no sabemos si saldrá escudo o corona, pero si conocemos los posibles
resultados. Cuando lanzamos un dado no sabemos el número que saldrá, pero sabemos que hay seis
posibles resultados. El resultado en el lanzamiento de una moneda o en el lanzamiento de un dado
depende del azar.
El lanzamiento de una moneda o de un dado es un fenómeno aleatorio. Qué el próximo niño que
nazca en una clínica sea niño o niña es un fenómeno aleatorio, pero la hora de la salida del sol o las
paradas por las que pasará el bus en la carretera no son fenómenos aleatorios porque conocemos de
antemano lo que va a suceder.
Llamamos fenómenos aleatorios a aquellos cuyos resultados dependen del azar. Es decir, son
Probabilidad
30
fenómenos que no se pueden predecir con certeza, mientras que aquellos que son predecibles se
llaman determinísticos.
Cada uno de los resultados de un fenómeno aleatorio se llama suceso.
Los sucesos posibles de lanzar dos monedas al aire son los que aparecen en el diagrama de árbol.
Figura 7
2.2.1
Experiencias Aleatorias
La probabilidad es un modelo matemático de los fenómenos aleatorios. Sin embargo, la cantidad de
fenómenos aleatorios es tan grande que una teoría que los abarque a todos es imposible; con el fin de
reducirlos se hablará en este trabajo de experiencias aleatorias.
Definición 2.1 (Experiencia Aleatoria)
Una experiencia aleatoria es un fenómeno que tiene tres características
1. Se conocen todos los posibles resultados antes de realizarse el experimento.
2. No se sabe cuál de los posibles resultados se obtendrá en un experimento particular.
3. El experimento puede repetirse.
Veamos un ejemplo donde se implementas estas definiciones
2.1
El lanzamiento de un dado es un fenómeno aleatorio estudiado por la probabilidad, pues
sus posibles resultados son 1, 2, 3, 4, 5 y 6. Además no se tiene certeza de cuál resultado
se obtiene al lanzar el dado, y el dado se puede lanzar varias veces se desee en condiciones
similares.
2.2 Conceptos básicos de probabilidad
Ejercicios 2.1
2.1 Formen equipos de 5 personas y discutan cuáles de los siguientes fenómenos o experi-
mentos se pueden repetir en condiciones similares y cuáles se pueden considerar experiencias
aleatorias.
1. Se lanza una moneda y se observa la cara (Escudo, corona) que queda hacia arriba
cuando queda en reposo.
Se puede repetir
No se puede repetir
¿Por qué?
¿Es una experiencia aleatoria?
2. Al lanzar un dado de seis puntos anotamos todos los resultados mayores que ocho.
Se puede repetir
No se puede repetir
¿Por qué?
¿Es una experiencia aleatoria?
3. En una bolsa metemos seis bolas rojas y seis azules, sacamos una y anotamos su color.
Se puede repetir
No se puede repetir
¿Por qué?
¿Es una experiencia aleatoria?
4. Al extraer una carta de la baraja observamos si sale un As. Se puede repetir
No se puede repetir
¿Por qué?
¿Es una experiencia aleatoria?
2.2.2
Espacio muestral y eventos
Definición 2.2 (Espacio Muestral)
Es el conjunto de todos los posibles resultados, este se denota: Ω
Definición 2.3 (Eventualidad)
Es un resultado particular, es decir un elemento de Ω : x es una eventualidad ⇔ x ∈ Ω
Definición 2.4 (Evento)
Es un conjunto de resultados, es decir un subconjunto de Ω : A es una evento ⇔ A ⊆ Ω
Definición 2.5 (Ocurrencia de un evento)
Se dice que un evento ocurre si sucede una y solo una de sus eventualidades.
31
Probabilidad
32
Definición 2.6 (Evento casi seguro)
Ω
Definición 2.7 (Evento casi imposible)
0/
2.2
Considere el experimento “Tirar un dado ” El espacio muestral es:
Ω = {1, 2, 3, 4, 5, 6}
Observe que 6 es una eventualidad. Algunos eventos son: A: el resultado del dado es impar, B
: el resultado del dado es mayor a 4
Note que:
A = {1, 3, 5} ⊆ Ω, B = {5, 6} ⊆ Ω
Si el resultado del dado es 3 entonces se dice que el evento A ocurre, el Evento B no ocurre.
Teorema 2.1 (Eventos Compuestos)
Si A y B son eventos entonces: A ∪ B, A ∩ B, A r B y A4B son eventos
2.3
Se tiene una canasta con 15 bolas enumeradas del uno al quince. Las bolas con número del 1
al 7 son rojas y las demás son verdes. Considere el experimento que consiste en elegir una
bola al azar de la canasta. Dados los eventos:
A: la bola elegida es verde
B : la bola elegida es roja
C : la bola elegida tiene un número par
entonces: el evento B ∪C ocurre si la bola elegida es roja o tiene número par, el evento A ∩C
ocurre si la bola elegida es verde con número par, el evento C r A ocurre si la bola elegida es
roja con número impar y el evento C4B ocurre si la bola elegida tiene número par ó es roja.
2.4
Una bolsa contiene bolas blancas y negras. Se extraen sucesivamente tres bolas.
2.2 Conceptos básicos de probabilidad
E = {(b, b, b); (b, b, n); (b, n, b); (n, b, b); (b, n, n); (n, b, n); (n, n, b); (n, n, n)}
Ejercicios 2.2
2.2 En los mismos grupos formados en los ejercicios 2.1, resuelva lo siguiente:
1. El suceso A = {extraer tres bolas del mismo color}.
2. El suceso B = {extraer al menos una bola blanca}.
3. Se lanza un dao una sola vez. Responda las siguientes preguntas:
a) ¿Puede ocurrir el evento formado por los resultados {1, 2, 3, 4, 5, 6}?
Si
No
¿Por qué?
b) ¿Puede ocurrir el evento formado por 1 o 2?
Si
No
¿Por qué?
c) ¿Es posible que ocurra el evento sale el número par y sale número primo?
Si
No
¿Por qué?
2.3 Considerar el experimento de lanzar dos dados de forma consecutiva y se registrar los
números que aparecen en cada dado (36 casos posibles).
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1),
(3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3),
(5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6))}
Marcar los resultados que corresponden a los siguientes eventos:
I ) Evento A = “No sale seis ”.
II )
Evento B = “Sale exactamente un seis”.
III )
Evento C = “Salen exactamente dos seis”.
IV )
Evento D = “Sale al menos un seis”.
33
Probabilidad
34
2.2.3
Álgebra de eventos
Sean A y B dos eventos de una experiencia aleatoria con espacio muestral Ω; a partir de esos dos
eventos se pueden definir en términos de la ocurrencia de A y B.
El evento complementario de A es el evento Ac , se dice que Ac ocurre cuando A no ocurre.
Se dice que A y B son eventos mutuamente excluyentes cuando no pueden ocurrir simultáneamente,
ésto es A ∩ B = 0/
2.3
Probabilidad
Dado un experimento, la probabilidad o medida de posibilidad de que ocurra un evento determinado
A será un número entre 0 y 1, que se interpreta como un porcentaje. Así si la probabilidad de A es
0.8, esto indica que el evento tiene un 80 % de posibilidad de ocurrir.
¿Cómo determinar intuitivamente la probabilidad de que ocurra un evento? Para que la probabilidad
sea útil debe existir una correspondencia entre la probabilidad y la realidad, es decir si el experimento
se repite varias veces, la frecuencia relativa observada con que ocurre un evento debe ser cercana
a la medida de la posibilidad de que ocurra ese evento. Está frecuencia relativa observada se le
llamará probabilidad frecuencial, la cual se espera que, bajo ciertas condiciones, se aproxime a la
probabilidad de que ocurra el evento (llamada probabilidad teórica)
Definición 2.8 (Definión clásica de probabilidad)
Ley de Laplace: Dado un experimento aleatorio con un espacio de n sucesos elementales Ω, la probabilidad del suceso A, que designamos mediante P(A), es la razón entre
la cantidad de casos favorables para la ocurrencia de A y la de casos posibles. En otros términos
P(A) =
|A|
|Ω|
2.5
Dado el fenómeno de lanzar un dado, ¿Cuál es la probabilidad de que salga un 6? Se lanza
un dado 100 veces y se observa que en 15 veces se obtiene un 6, por lo tanto la probabilidad
15
frecuencial observada de obtener un 6 es
= 15 % que es cercana a la probabilidad teórica
100
1
de = 16.6 %, la que en las próximas secciones veremos cómo obtener. Pero, ¿cuántas veces
6
debe repetirse el experimento para que la probabilidad frecuencial se acerque a la real?
2.3 Probabilidad
35
2.6 (¿Juegas o no?)
En las fiestas cívicas de Zapote hay un puesto donde por 1000 colones se puede jugar DADOS
A SEIS.
Este juego consiste en lazar dos dados distintos, si la suma de los resultados de los
dados es menor igual a 6 se gana el juego sino se pierde.
Karla, Jorge y Anthony desean determinar si vale la pena jugar el juego, para ello
deciden que cada uno juegue veinte veces DADOS A SEIS obteniendo los siguientes
resultados: # de veces que se ganó Probabilidad frecuencial de ganar ¿Vale la pena Jugar?
# de veces que se ganó
probabilidad frecuencial
de ganar
¿Vale lapena
jugar?
Karla
7
7
= 35 %
20
No
Jorge
10
10
= 50 %
20
Es Indiferente
Anthony
12
12
= 60 %
20
Si
Se puede apreciar que los resultados obtenidos utilizando la probabilidad frecuencial son muy
distintos. Tal parece que algunas probabilidades frecuenciales no se acercar al valor real de la
probabilidad. ¿Cuál es realmente la probabilidad de ganar DADOS A SEIS?
El último ejemplo revela que no necesariamente la probabilidad frecuencial se va a acercar a la probabilidad real. Entonces ¿qué condiciones deben cumplirse para que la frecuencia relativa observada
se acerque a la probabilidad teórica? Las condiciones las establece la Ley de los Grandes Números:
Dado un experimento, sea A un evento. Si el experimento se repite un número suficientemente grande
de veces, entonces la probabilidad frecuencial de A será muy cercana al valor real de la probabilidad.
Curiosidades
1
El naturalista francés Count Buffon (1707-1788) lanzó una moneda 4040 veces.
Resultado: 2048 caras, proporción 2048/4040=0,5069 o 50,69 % de caras.
2
Alrededor del 1900, el estadístico inglés Karl Pearson ¡lanzó una moneda 24 mil veces!
Resultado: 12012 caras, proporción 12012/24000=0,5005 o 50,05 % de caras.
3
Durante la II guerra mundial, el matemático australiano John Kerrich, mientras
estaba en prisión lanzó una moneda 10 mil veces. Resultado: 5067 caras, proporción
5067/10000=0,5067 o 50,67 % de caras.
Probabilidad
36
Definición 2.9 (Condiciones de una Probabilidad)
Si Ω es el espacio muestral y A es un evento, entones:
1. 0 ≤ P(A) ≤ 1
2. P(0)
/ = 0 y P(Ω) = 1
3. P(a1 ) + P(a2 ) + . . . + P(an ) = 1; donde Ω = {a1 , a2 , . . . , an }
2.7
Lanzamos un dado normal al aire. Consideramos el suceso A= “sale par”. Calcular P(A).
Casos posibles hay 6, pues
Ω = {1, 2, 3, 4, 5, 6}
.
Casos favorables al suceso
A = {2, 4, 6}
Por tanto
P(A) =
3 1
= = 0,5
6 2
(Notemos que la probabilidad siempre es un número positivo y menor, o a lo sumo, igual a 1).
Ejercicios 2.3
2.4 De una urna que contiene 8 bolas rojas, 5 amarillas y 7 verdes se extrae una bola al azar.
Calcula la probabilidad de que la bola extraída sea
a.) roja
b.) verde
c.) amarilla
2.5 Una caja contiene una bola roja, una negra y una verde. Considerar el experimento sacar
dos bolas de la siguiente manera: se extrae una bola al azar y sin restituirla se saca otra bola al
azar. Considere los siguientes eventos:
A0 ={no se obtiene ninguna bola roja}
A1 ={ se obtiene exactamente una bola roja}
A2 ={ se obtienen dos bolas rojas}
Encontrar las probabilidades de A0 , A1 , A2
2.6 Se lanzan dos dados no cargados de manera simultanea, determine:
2.3 Probabilidad
37
¿Cuál es la probabilidad de obtener dos pares? R/ 14
¿Cuál es la probabilidad de obtener suma par?R/ 21
¿Cuál es la probabilidad de obtener suma impar?R/ 21
¿Cuál es la probabilidad de obtener un 2 o un 5?
¿Cuál es la probabilidad de obtener suma mayor que 4?
2.7 Se arrojan dos dados. Sea A el evento de que la suma de las caras es impar; B el evento
de que sale por lo menos un número 1. Describir los eventos:
a.) A ∪ B
b.) A ∩ B
c.) A ∩ Bc
2.8 Una rifa del cole consiste en sacar una ficha al azar de una urna que contiene 100 fichas
enumeradas del 1 al 100. Se define el evento A como el número de la ficha extraída que
contenga entre sus dígitos la cifra 5. Calcular:
a.) P(A)
b.) P(Ac )
a.)
b.)
c.)
d.)
e.)
2.3.1
Función de probabilidad
Para definir la función de probabilidad, que toma un evento y le asigna un valor que indique la
posibilidad de ocurrencia, es necesario poner condiciones sobre su dominio, el cual es un conjunto
de eventos o sea un subconjunto de P(Ω).
2.3.2
Espacio probabilizable o σ −algebra
Definición 2.10 (σ −algebra)
Sea A un conjunto de eventos, es decir A ⊆ P(Ω)a . Se dice que A es un espacio probabilizable
o una σ −algebra sobre Ω si y solo si cumple los siguientes axiomas:
Axioma 1 Ω ∈ A
Axioma 2 X ∈ A ⇒ X ∈ A
Axioma 3 X,Y ∈ A ⇒ X ∪Y ∈ A
a Se
denota con P(X) el conjunto de subconjuntos de Ω, para diferenciarlo de P(X), la probabilidad de X
2.8
Los conjuntos
{0,
/ Ω} y P(Ω)
son σ −algebra sobre Ω.
Probabilidad
38
2.3.3
Regla de la suma
Teorema 2.2 (Regla de la suma)
La probablidad de la suma de dos sucesos mutuamente excluyentes (incompatibles )A y B es
la suma de sus probabilidades, es decir
P(A ∪ B) = P(A) + P(B)
Decimos que los sucesos A1 , . . . , Am son incompatibles dos a dos cuando todas las parejas posibles
de sucesos distintos son incompatibles, es decir, cuando Ai ∩A j = 0.
/
Si A, B y C son tres sucesos incompatibles no es difícil establecer, teniendo en cuenta el teorema
anterior, que
P(A ∪ B ∪C) = P(A) + P(B) + P(C).
Más en general, si A1 , . . . , An son sucesos incompatibles dos a dos, la regla de la suma es la fórmula
n
P(A1 ∪ . . . ∪ An ) = P(A1 ) + . . . + P(An ) = Xn =
∑
P(An )
k=1
Esta fórmula incluye a las dos anteriores en los casos en que n = 2 y n = 3, y se demuestra mediante
la aplicación sucesiva de la fórmula.
2.3.4
Propiedades de la probabilidad
La definición de probabilidad junto a la regla de la suma permiten obtener importantes propiedades
para el cálculo de probabilidades.
Propiedad 1
Para cualquier suceso A se tiene P(A) = 1 − P(A).
Propiedad 2
Si A ⊂ B, entonces P(A) ≤ P(B).
Propiedad 3
Para sucesos A y B arbitrarios vale la igualdad P(A ∪ B) = P(A) + P(B) − P(A ∩ B).
N
Importante:
A Si los sucesos A yB son incompatibles, entonces P(A ∩ B) = 0, y de la propiedad 3 se
obtiene la igualdad ya conocida P(A ∪ B) = P(A) + P(B).
B
En forma análoga, no es difícil demostrar, que para tres sucesos A, B y C arbitrarios,
tiene lugar la igualdad
P(A ∪ B ∪C) = P(A) + P(B) + P(C) − P(A ∩ B) − P(A ∩C) − P(B ∩C) + P(A ∩ B ∩C).
2.3 Probabilidad
39
2.9
Se tira una moneda 3 veces. Calcular la probabilidad de obtener alguna cara.
Los problemas de este tipo, en los que se pide la probabilidad de obtener “alguna” cosa, se
suelen resolver muy bien por paso al complementario. En este caso concreto, A = “obtener
alguna cara”.
A= “no obtener ninguna cara”= “obtener 3 cruces”.
1
Entonces, p(A) = , pues hay 8 casos posibles (2·2·2, ¡haz el diagrama de árbol!) y sólo uno
8
favorable (XXX, 3 cruces), por tanto:
p(A) = 1 − p(A) = 1 −
1 7
=
8 8
2.10
Se lanza un dado dos veces y se suman las dos caras. Sea A el suceso A=“la suma de resultados
es mayor o igual que 10” y B= “la suma de los resultados es múltiplo de 6”. Calcular p(A),
p(B) y p(A ∩ B).
Hay 36 posibles resultados al lanzar dos veces un dado. ¿Cuántos de ellos suman 10 o más?
Que sumen 10: (4,6), (5,5), (6,4)
Que sumen 11: (5,6), (6,5)
Que sumen 12: (6,6)
Por tanto,
p(A) =
6
1
=
36 6
¿Cuántos hay que sumen múltiplo de 6?
Que sumen 6: (1,5), (2,4),(3,3), (4,2), (5,1)
Que sumen 12: (6,6)
6
1
Por tanto, p(B) =
=
36 6
En cuanto a A ∩ B = (6, 6), luego
p(A ∩ B) =
1
6
.
Para la siguiente actividad se solicita reunirse en grupos de 4 personas
Probabilidad
40
Ejercicios 2.4
2.9 Se ha encargado la impresión de una encuesta a una imprenta, que imprime 12 folios
defectuosos de cada 1000. Hallar la probabilidad de que elegido un folio de la encuesta al
azar:
a.) Esté mal impreso.
b.) Esté correctamente impreso
2.10 Una bolsa contiene 8 bolas numeradas. Se extrae una bola y anota su número. Sean los
sucesos:
A= “salir par”, B= “salir impar”, C= “salir múltiplo de 4”.
Calcular las probabilidades de A ∪ B, A ∪C, B ∪C, A ∪ B ∪C.
2.11 En el banquete posterior a una boda se sientan en la presidencia 10 personas, entre los
cuales se encuentran los novios. Calcular la probabilidad de que los novios estén juntos en el
centro de la mesa.
2.3.5
Regla de multiplicación de probabilidades
Si se tienen varios eventos sucesivos e independientes entre sí, la probabilidad de que ocurran todos
ellos a la vez corresponde a la multiplicación de las probabilidades de cada uno de los eventos.
2.11
Si se responden al azar cuatro preguntas con cinco opciones cada una, ¿cuál es la probabilidad
de acertar a todas?
La probabilidad de acierto en cada una de las preguntas es 1/5. Por lo tanto, la probabilidad de
acertar en las cuatro es:
1
1 1 1 1
P(A) = · · · =
5 5 5 5 625
2.12
1
Suponiendo que la probabilidad de tener un hijo o una hija es , ¿cuál es la probabilidad de
2
que al tener tres hijos, 2 solamente sean varones?
Si H representa el nacimiento de un hombre y M el de una mujer, tenemos los siguientes
casos favorables: HHM − HMH − MHH
3
1
1
La probabilidad de cada uno de estos eventos es:
=
2
8
2.3 Probabilidad
2.3.6
41
Probabilidad condicionada
Hasta ahora nos hemos limitado a calcular probabilidades únicamente partiendo de un experimento
aleatorio, sin tener más información. Pero, ¿qué ocurre si conocemos alguna información adicional?.
A menudo se requiere calcular la probabilidad de un evento A sabiendo de antemano que ha ocurrido
otro evento, digamos B.
Esta nueva probabilidad, que se denota por P(A|B), se llama la probabilidad condicional de A dado
el evento B. Estudiaremos un ejemplo antes de dar una definición formal de este concepto.
2.13
Consideremos el lanzamiento de tres monedas. Sabemos que el espacio muestral correspondiente es:
S = {ccc, cce, cec, ecc, cee, ece, eec, eee}.
Sean A y B los eventos definidos como A: “ cae a lo más una corona” B: “en la primera moneda cae
corona”.
Es claro que A = {eee, cee, ece, eec} y B = {ccc, cce, cec, cee}.
Véase la Figura 8:
Figura 8
Supóngase que deseamos calcular la probabilidad de que al lanzar tres monedas cae a lo más una
corona, pero por otra parte, en alguna forma nos hemos enterado de que la primera moneda cayó
corona. Antes de conocer esta información, cada uno de los eventos eee, cee, ece, eec tenía probabilidad 1/8. Pero ahora nuestro espacio muestral se ha “restringido”; es decir, sabemos ya que el
evento B ha ocurrido (la primera moneda cayó corona).
Luego, la única forma en que puede ocurrir que cae a lo más una corona es que ocurra el resultado
cee, cuya probabilidad es ahora 1/4, pues B consta de 4 resultados únicamente. Así pues, P(A) = 4/8,
pero P(A|B) = 1/4.
Analizaremos con más cuidado la situación: si deseamos calcular la probabilidad de A (“cae a lo
más un corona”) dado que el evento B (“en la primera moneda cae corona”) ha ocurrido, entonces
podemos suponer que nuestro espacio muestra no es todo S, sino únicamente el conjunto B, y en este
Probabilidad
42
caso, P(A|B)es la probabilidad de los resultados que están en A y en B con respecto al nuevo “espacio
muestral” B. En particular, si el espacio S es equiprobable, entonces B también lo es y tendremos que:
P(A|B) =
P(A ∩ B)
P(B)
(1)
Volviendo al ejemplo 2.13, como A ∩ B = {cee}, vemos que P(A ∩ B) = 1/8. Asimismo P(B) = 4/8.
Luego se tiene:
(A|B) =
1/8
= 1/4
4/8
Definición 2.11
Sean A y B eventos en un espacio muestral S y supóngase que P(B) > 0. EntoncesP(A|B), la
probabilidad condicional del evento A dado el evento B, se define como
P(A|B) =
P(A ∩ B)
P(B)
Aunque esta fórmula es importante en sí misma tiene la ventaja adicional de que nos da una expresión
para la probabilidad de la intersección de dos eventos. En efecto, de (1),
P(A ∩ B) = P(B)P(A|B),
(2)
o bien, puesto que P(B|A) = P(B ∩ A)/P(A), también podemos escribir
P(A ∩ B) = P(A)P(B|A).
(3)
Nota: Para evitar repeticiones, al hablar de la probabilidad condicional P(A|B) siempre supondremos que P(B) > 0.
La expresión (2) o la (3) se conoce también como teorema de la multiplicación y se puede extender
a cualquier número finito de eventos, o sea,
P(A1 ∩ A2 ∩ · · · ∩ An ) = P(A1 )P(A2 |A1 )P(A3 |A1 ∩ A2 ) · · · P(An |A1 ∩ A2 ∩ · · · ∩ An?1 ).
Por ejemplo, para n = 3,
P(A1 ∩ A2 ∩ A3 ) = P(A1 )P(A2 |A1 )P(A3 |A1 A2 ).
(4)
2.14
De una clase de 8 varones y 6 mujeres se seleccionan al azar tres estudiantes, uno tras otro.
¿Cuál es la probabilidad de que los tres sean varones?
Solución: En otras palabras, deseamos calcular la probabilidad
2.3 Probabilidad
43
P(A1 ∩ A2 ∩ A3 ),
en donde Ai es el evento: “el i-ésimo estudiante selecionado es varón”, i = 1, 2, 3.
Como en total son 14 estudiantes, de los cuales 8 son varones, P(A1 ) = 8/14. Si el primer estudiante
seleccionado fue varón, quedan 13 estudiantes, de los cuales 7 son varones. Por lo tanto, P(A2 |A1 ) =
7/13. Análogamente, la probabilidad de que el tercer estudiante seleccionado sea varón dado que los
dos primeros eran varones es
P(A3|A1 ∩ A2) = 6/12. (¿Por qué?)
Luego, de (4),
P(A1 ∩ A2 ∩ A3 ) =
2
8 7 6
· ·
=
14 13 12 13
2.15
En un aula hay 100 alumnos, de los cuales: 40 son hombres, 30 usan gafas, y 15 son varones y
usan gafas. Si sabemos que el alumno seleccionado no usa gafas, ¿qué probabilidad hay de
5
que sea hombre? R P(h|gc ) =
14
En grupos de 5 personas resuelva los siguientes ejercicios
Ejercicios 2.5
2.12 Consideremos una urna que contiene 4 bolillas rojas y 5 blancas. De las 4 bolillas rojas,
2 son lisas y 2 rayadas y de las 5 bolillas blancas, 4 son lisas y una sola es rayada. Supongamos
que se extrae una bolilla y, sin que la hayamos mirado, alguien nos dice que la bolilla es roja,
¿cuál es la probabilidad de que la bolilla sea rayada? R/ 0.5
2.13 Consideremos una población en la que cada individuo es clasificado según dos criterios:
es o no portador de HIV y pertenece o no a cierto grupo de riesgo que denominaremos R. La
correspondiente tabla de probabilidades es:
Pertenece a R (B)
No pertenece a R (Bc )
Portador (A)
0.003
0.003
0.006
No portador (Ac )
0.017
.977
0.994
0.020
0.980
1.000
Dado que una persona seleccionada al azar pertenece al grupo de riesgo R,
a.) ¿cuál es la probabilidad de que sea portador? R/ 0.150
b.) ¿Cuál es la probabilidad de que una persona sea portadora de HIV, dado que no pertenece
al grupo de riesgo R?./R 0.00306
2.14 Se lanzan dos dados:
a.) ¿Cuál es la probabilidad de obtener una suma de puntos igual a 7? R/ 1/6
Probabilidad
44
b.) Si la suma de puntos ha sido 7, ¿cuál es la probabilidad de que en alguno de los dados
haya salido un tres?R/ 1/3
2.3.7
Teorema de la probabilidad total
Si E es un evento en un espacio muestral S, es posible conocer P(E) en términos de las probabilidades
condicionales de los eventos en una partición de S. Decimos que los eventos en S
A1, A2 , · · · , An
forman una partición de S si estos conjuntos son ajenos por parejas y su unión es S; es decir,
a) Ai ∩ A j = 0/ ; si i 6= j,
b) S = ni=1 Ai = A1 ∪ A2 ∪ · · · ∪ An
El nombre de “partición” es muy sugestivo; nos dice que los eventos A1 , A2 , · · · , An dividen (particionan o “parten”) el espacio S en conjuntos ajenos (Ver figura 9)
S
Ahora, sea A1 , A2 , · · · , An una partición de S, y sea E un evento cualquiera en S. Es claro que E se
puede escribir como una unión de conjuntos ajenos:
E = (E ∩ A1 ) ∪ (E ∩ A2 ) ∪ · · · ∪ (E ∩ An ).
Figura 9
Entoces por la propiedad aditiva
P(A ∪ B ∪C) = P(A) + P(B) + P(C).
se tiene que
P(E) = P(E ∩ A1 ) + P(E ∩ A2 ) + · · · + P(E ∩ An ).
Finalmente, por el teorema de multiplicación
P(E) = P(A1 )P(E|A1 ) + P(A2 )P(E|A2 ) + · · · + P(An )P(E|An ),
2.3 Probabilidad
45
o en forma más compacta:
n
P(E) = ∑ P(Ai )P(E|Ai )
i=1
Este resultado se conoce como teorema de la probabilidad total.
2.16
En una fábrica, tres máquinas, M1, M2, M3 elaboran respectivamente el 30 %, el 50 % y el
20 % de la producción total. Los porcentajes de artículos defectuosos producidos por estas
máquinas son 1 %, 3 %, 2 %, respectivamente. Si se selecciona un artículo al azar, calcule la
probabilidad de que sea:
(a) Defectuoso
(b) No defectuoso
Solución: Si denotamos por Ai el evento: “el artículo seleccionado fue producido por la máquina
Mi ” , i = 1, 2, 3, es claro que A1 , A2 y A3 forman una partición del espacio muestral
que resulta del
experimento de tomar un artículo y ver si es defectuoso (d) o no defectuoso de . ; E ∩ Ai sería el
evento: “el artículo es defectuoso y fue elaborado en la máquina Mi ”, i = 1, 2, 3. En la Figura 10
aparece un diagrama de árbol que ilustra el problema.
(a) Con probabilidades 0.3, 0.5 y 0.2, respectivamente, el artículo puede ser de cualquiera de las
máquinas M1 , M2 , M3 . Además, dependiendo de la máquina en que se elaboró, el artículo tiene
probabilidades 0.01, 0.03 y 0.02 de ser defectuoso. Entonces
P(d) = P(A1 )P(d|A1 ) + P(A2 )P(d|A2 ) + P(A3 )P(d|A3 ) =
(0,3)(0,01) + (0,5)(0,03) + (0,2)(0,02) = 0,022.
e = 1 − P(d) =
(b) El evento “no defectuoso” es el complemento del evento “defectuoso”. Luego, P(d)
0,978.
Figura 10
Probabilidad
46
2.17
En un colegio se imparten sólo los idiomas inglés y francés. El 80 % de los alumnos estudian
inglés y el resto francés. El 30 % de los alumnos de inglés son socios del club musical del
colegio y de los que estudian francés son socios de dicho club el 40 %. Se elige un alumno al
azar.
Calcular la probabilidad de que pertenezca al club musical.
Solución
En estos problemas es importante elegir el sistema completo de sucesos. En este caso: A1 = estudiar
inglés
A2 = estudiar francés
B= ser del club musical.
Nos piden p(B). Por el teorema anterior:
p(B) = p(A1 ) · p(B/A1 ) + p(A2 ) · p(B/A2 ) =
20 40
80 30
·
+
·
=
100 100 100 100
8
25
= 0,32
Mediante el diagrama de árbol:
Figura 11
Se obtiene el mismo resultado
2.3.8
Sucesos independientes
Si bien el conocer cierta información adicional modifica la probabilidad de algunos sucesos, puede
ocurrir que otros mantengan su probabilidad, pese a conocer dicha información.
2.18
En el lanzamiento de un dado, consideremos los sucesos: A=“ sacar un número par” y B=
“sacar un número menor o igual que 2”. Es claro que A = {2, 4, 6} y B = {1, 2}.
2.3 Probabilidad
47
Calculemos la probabilidad de A conociendo que se ha realizado el suceso B, es decir,p(A/B).
p(A/B) =
p(A ∩ B)
= 0,5
p(B)
1
1
puesto que p(A ∩ B)=p(sacar par y menor o igual que 2)= y p(B) = .
6
3
Pero si no conociésemos la información B, ¿cuál sería la probabilidad de A?.
3
p(A)=p(sacar par)= = 0,5, es decir que p(A/B) = p(A), y por tanto el conocer la información
6
B no modifica la probabilidad de A.
Cuando esto ocurre es decir, cuando p(A/B) = p(A), diremos que los sucesos A y B son independientes (el hecho de que ocurra B no modifica la probabilidad de A).
Propiedad 4
A y B son sucesos independientes ⇔ P(A ∩ B) = p(A) · (B)
Teorema 2.3 (Eventos Independientes)
A y B son eventos independientes si y solo si P(A|B) = P(A)
Teorema 2.4 (Regla del producto 2)
En general se cumple que P(A1 ∩ A2 ∩ · · · ∩ An ) = P(A1 ) · P(A2 |A1 ) · P(A2 |(A1 ∩ A2 )) . . . ·
P(An |(A1 ∩ A2 ∩ . . . ∩ An−1 ))
Probabilidad
48
Algunos ejemplos de eventos independientes
Figura 12
2.19
Una caja contiene 4 canicas rojas, 3 canicas verdes y 2 canicas azules. Una canica es eliminada
de la caja y luego reemplazada. Otra canica se saca de la caja. Cuál es la probabilidad de que
la primera canica sea azul y la segunda canica sea verde?
Solución
Ya que la primera canica es reemplazada, el tamaño del espacio muestral (9) no cambia de la primera
sacada a la segunda así los eventos son independientes.
P(azul ∩ verde) = P(azul) · P(verde) =
2 3
2
· =
9 9 27
2.20
En una escuela el 20 % de los alumnos tiene problemas visuales, el 8 % tiene problemas
auditivos y el 4 % tienen tanto problemas visuales como auditivos, Sean: V los que tienen
problemas visuales y V C los que no lo tienen. A los que tienen problemas auditivos y AC los
que no los tienen.
a) ¿Son los dos eventos de tener problemas visuales y auditivos, eventos independientes?
b) ¿Cuál es la probabilidad de que un niño tenga problemas auditivos si sabemos que tiene
problemas visuales?
2.3 Probabilidad
49
V
V c total
0,04
0,08
A
Ac
Total 0,20
1,00
d) ¿Cuál es la probabilidad de que un niño no tenga problemas auditivos si tiene problemas
visuales?
c) Complete la siguiente tabla
Solución
a. P(V )P(A) = (0,2)(0,08) = 0,016yP(V ∩ A) = 0,04. Como P(V ∩ A) 6= P(V )P(A), se concluye
que V y A no son independientes.
P(A ∩V )
0,04
P(V ) =
= 0,20
0,02
c. Por diferencias podemos completar la tabla, ya que P(V C ) = 1?0,20 = 0,80 y P(AC ) = 1?0,08 =
0,92, por lo tanto
d.
V
V c total
A
0,04 0,04 0,08
c
A
0,16 0,76 0,92
Total 0,20 0,80 1,00
P(Ac ∩V ) 0,16
e. P(Ac |V ) =
=
= 0,80
P(V )
0,02
b. P(A|V ) =
Ejercicios 2.6
2.15 Se tiene una urna con 12 bolas enumeradas del 1 al 8. Considere la experiencia aleatoria
de extraer bolas de la urna, al azar y de una en una, de acuerdo con la siguiente regla:
si la bola extraída tiene un número impar se retorna a la urna antes de la siguiente
extracción,
Se finaliza cuando se halla extraído, con o sin reposición, dos bolas con números
impares. en caso contrario no se retorna.
a.) ¿Cuál es la probabilidad de extraer 4 bolas en total?
b.) Considere los eventos
Ii : la i-ésima bola extraída es impar.
Pi : la i-ésima bola extraída es par.
Calcule la probabilidad:
P((I1 P2 P3 I4 ) ∪ (P1 P2 I3 I4 ) ∪ (P1 I2 P3 I4 ))
R/ 73/294
Probabilidad
50
2.3.9
La ley de los grandes números
La ley de los grandes números, también llamada ley del azar, afirma que al repetir un experimento
aleatorio un número de veces, la frecuencia relativa de cada suceso elemental tiende a aproximarse a
un número fijo, llamado probabilidad de un suceso.
Observa la siguiente tabla, en la que se han anotado las frecuencias del suceso “salir cara al lanzar
una moneda”.
Figura 13
Al aumentar los lanzamientos, las frecuencias relativas se aproximan a un valor 0.5. Ésa es la
probabilidad del suceso salir cara al lanzar una moneda.
La probabilidad de un suceso es el número al que se aproxima su frecuencia relativa cuando el
experimento se repite un gran número de veces.
Figura 14
2.3.10
Teorema del Límite Central
El Teorema Central del Límite dice que si tenemos un grupo numeroso de variables independientes
y todas ellas siguen el mismo modelo de distribución (cualquiera que éste sea), la suma de ellas se
distribuye según una distribución normal.
2.3 Probabilidad
51
La variable “tirar una moneda al aire” sigue la distribución de Bernouilli. Si lanzamos la moneda al
aire 50 veces, la suma de estas 50 variables (cada una independiente entre si) se distribuye según una
distribución normal.
Este teorema se aplica tanto a suma de variables discretas como de variables continuas.
Los parámetros de la distribución normal son:
Media: n · µ (media de la variable individual multiplicada por el número de variables independientes)
Varianza: n · σ 2 (varianza de la variable individual multiplicada por el número de variables individuales)
2.21
Se lanza una moneda al aire 100 veces, si sale cara le damos el valor 1 y si sale cruz el
valor 0. Cada lanzamiento es una variable independiente que se distribuye según el modelo
de Bernouilli, con media 0,5 y varianza 0,25. Calcular la probabilidad de que en estos 100
lanzamientos salgan más de 60 caras.
La variable suma de estas 100 variables independientes se distribuye, por tanto, según una distribución normal. Media = 100 · 0, 5 = 50
Varianza = 100 · 0, 25 = 25
Para ver la probabilidad de que salgan más de 60 caras calculamos la variable normal tipificada
equivalente:
Y=
60 − 50
=2
5
Nota: 5 es la raiz cuadrada de 25, o sea la desviación típica de esta distribución.
Por lo tanto:
P(X > 60) = P(Y > 2, 0) = 1 − P(Y < 2, 0) = 1 − 0, 9772 = 0, 0228
Es decir, la probabilidad de que al tirar 100 veces la moneda salgan más de 60 caras es tan sólo del
2,28 %.
2.22
La renta media de los habitantes de un país se distribuye uniformemente entre 4,0 millones
ptas. y 10,0 millones ptas. Calcular la probabilidad de que al seleccionar al azar a 100 personas
Probabilidad
52
la suma de sus rentas supere los 725 millones ptas.
Cada renta personal es una variable independiente que se ditribuye según una función uniforme. Por
ello, a la suma de las rentas de 100 personas se le puede aplicar el Teorema Central del Límite.
La media y varianza de cada variable individual es:
µ = (4 + 10)/2 = 7
σ 2 = (10 − 4)2 /12 = 3
Por tanto, la suma de las 100 variables se distribuye según una normal cuya media y varianza son:
Media: n · µ = 100 · 7 = 700
Varianza: n · σ 2 = 100 · 3 = 300
Para calcular la probabilidad de que la suma de las rentas sea superior a 725 millones ptas, comenzamos por calcular el valor equivalente de la variable normal tipificada:
Y=
725 − 700
= 1,44
17,5
Luego:
P(X > 725) = P(Y > 1, 44) = 1 − P(Y < 1, 44) = 1 − 0, 9251 = 0, 0749
Es decir, la probabilidad de que la suma de las rentas de 100 personas seleccionadas al azar supere
los 725 millones de pesetas es tan sólo del 7,49 %
[1] Barreras, Miguel (2008).¡AH!, EL AZAR? Recopilado el 14 de junio del 2013 de:
http://ocw.uniovi.es/file.php/66/Elazar.pdf
[2] Batanero, C. (2013).La comprensión de la probabilidad en los niños. ¿Qué podemos
aprender de la investigación? En J. A. Fernandes, P. F. Correia, M. H. Martinho, & F.
Viseu, (Eds..) (2013). Atas do III Encontro de Probabilidades e Estatística na Escola.
Braga: Centro de Investigação em Educação. Universidade Do Minho.
[3] Hernández, José (2007). EStadística Administrativa I. Instituto Tecnològico de Apizaco. México.Recopilado el 16 de junio del 2013 de: http:
//www.itapizaco.edu.mx/~joseluis/apuntes/estadistica/estadistica%
20administrativa%20I.pdf
[4] Hopkins, K.; Hopkins, B.; Glass, G.(1997).Estadística básica para las ciencias sociales
y del comportamiento. Prentice-Hall Hispanoamericana, Naucalpán de Juarez. México.
[5] Molina, M; Rodrigo, M. (2010). Estadísticos de dispersión. Universidad de Valencia. España. Recopilado el 20 de setiembre del 2014 de: http://ocw.uv.es/
ciencias-de-la-salud/pruebas-1/1-3/t_04.pdf
[6] Pajares, A.; Tomeo, V. (2009). Enseñanza de la Estadística y la Probabilidad en
Secundaria: experimentos y materiales. En M. J. González; M. T. González y J. Murillo (eds.), Investigación en Educación Matemática. Comunicaciones de los grupos de investigación. XIII Simposio de la SEIEM. Santander.Recopilado el 16 de
junio del 2013 de: http://estudiosestadisticos.ucm.es/data/cont/docs/
12-2013-02-06-CT03_2009.pdf
[7] Trejos, J.; Moya, E. (2012). Introducción a la Estadística Descriptiva.Ediciones el
Roble. Costa Rica.
54
BIBLIOGRAFÍA
[8] Triolla, F.(2013). Estadística.Editorial Pearson. México.
[9] (s.a.). (2013) .Varianza y desviación estándar. La desviación sólo significa qué
tan lejos de lo normal. Recopilado el 20 de setiembre del 2014 de: http://www.
disfrutalasmatematicas.com/datos/desviacion-estandar.html