TALLER-PARA-RECUPERAR-GRADO-10º-3
Anuncio

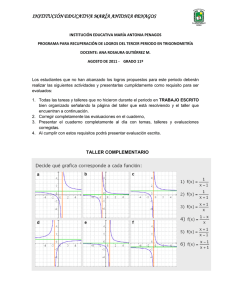
INS IÓN EDUCAT TITUC IVA INSTITUCIÓN EDUCATIVA MARÍA ANTONIA PENAGOS Ma. ANTO NIA PENAGOS PALMIRA INSTITUCIÓN EDUCATIVA MARÍA ANTONIA PENAGOS PROGRAMA PARA RECUPERACIÓN DE LOGROS DEL TERCER PERIODO EN TRIGONOMETRÍA DOCENTE: ANA ROSAURA GUTIÉRREZ M. AGOSTO DE 2011 - GRADO 10º Los estudiantes que no han alcanzado los logros propuestos para este periodo deberán realizar las siguientes actividades y presentarlas cumplidamente como requisito para ser evaluados: 1. Todas las tareas y talleres que no hicieron durante el periodo en TRABAJO ESCRITO bien organizado señalando la página del taller que está resolviendo y el taller que encuentran a continuación. 2. Corregir completamente las evaluaciones en el cuaderno, 3. Presentar el cuaderno completamente al día con temas, talleres y evaluaciones corregidas. 4. Al cumplir con estos requisitos podrá presentar evaluación escrita. TALLER COMPLEMENTARIO 1. Resolver el triángulo ∆ en el que dos de sus ángulos meden α = 30º, β = 105º y el lado opuesto al tercer ángulo mide c = 10 cm 2. Resolver los siguientes triángulos: a. b. c. d. e. f. g. a = 325 m, A = 30° y C = 87° b = 601 m, c = 1000 m y C = 95° a = 40 cm, b = 38 cm y c = 27 cm a = 12,33 cm, c = 24,05 cm y B = 76° a = 11 cm, b = 6 cm y C = 42º a = 7m, c=8m y B = 52º b = 10 m, c = 15m y A = 123º 3. Analiza cada situación y luego resuelve utilizando teorema de Seno o Coseno según convenga. A. Dos observadores A y B ven un globo cautivo que está situado en un plano vertical que pasa por ellos. La distancia entre ellos es de 4 Km. Los ángulos de elevación del globo desde los observadores son 45º y 75º respectivamente. Calcula la altura del globo. B. Un río tiene las dos orillas paralelas. Desde los puntos A y B de una orilla se observa un punto C de la orilla opuesta; las visuales forman con la INS IÓN EDUCAT TITUC IVA INSTITUCIÓN EDUCATIVA MARÍA ANTONIA PENAGOS Ma. ANTO NIA PENAGOS PALMIRA dirección de la orilla unos ángulos de 45º y 60º, respectivamente. Calcula la anchura del río sabiendo que la distancia entre los puntos A y B es de 30m. C. Desde la cúspide de un faro de 80 m. De altura, se observan hacia el oeste dos botes según ángulos de depresión de 60o y 30o. Calcule la distancia que separa a los botes. D. Un niño está haciendo volar dos cometas simultáneamente. Uno de ellos tiene 380 m y la otra 420m de hilo. Se supone que el ángulo entre los dos hilos es de 30o. Estime la distancia entre las dos cometas. E. Dos trenes parten simultáneamente de una estación en dirección tal que forma un ángulo de 15º. Uno va a 15 km/h y el otro a 25 km/h. Determina qué distancia los separa después de 3 horas de viaje. 4. Utilizando las fórmulas para la suma de ángulos calcula la razón del ángulo indicado. d) Cos 130º a) Cos 210º e) Tan 305º b) Sen 345º f) Tan 118º c) Sen 50º 5. Utilizando las fórmulas para la diferencia de ángulos, calcula el valor de la razón trigonométrica para el ángulo que se indica a) Cos 128º d) Sen 130º g) Cos 85º b) Sen 98º e) Cos 350º h) Sen 248º c) Tan 105º f) Tan 205º i) Tan 98º 6. Encuentra el valor de la diferencia de ángulos. a) b) c) d) e) f) razón trigonométrica indicada para la suma y la Cos (325º - 80º) Sen (180º + 20º) Sen (90º - 10º) Cos (130º + 60º) Tan(150º - 45º) Tan(95º + 65º) NOTA: RECUERDEN QUE AQUELLOS ESTUDIANTES QUE SOLO RECUPERAN LA EVALUACIÓN O LAS EVALUACIONES PERDIDAS, ÚNICAMIENTE PRESENTAN ESTE TALLER Y LAS CORRECCIONES, COMO REQUISITO PARA LA EVALUACIÓN.