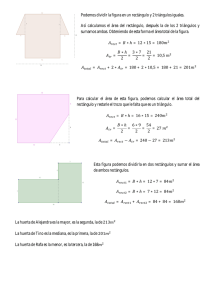
UNIDAD I: “La proporcionalidad y el diseño”

Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
DISEÑO DE INTERIORES Y MOBILIARIO
ASIGNATURA: MATEMÁTICA
Alicia M. Iturbe Cecilia Ariagno
UNIDAD I: “La proporcionalidad y el diseño”
“El Modulor” de Le
Corbousier
Estudio anatómico basado en
la proporción áurea
Propósito
Estudiar la proporcionalidad, haciendo hincapié en la
vinculación que existe entre ciertos principios de la
misma con conceptos estéticos y morfológicos del
diseño.
Contenidos
Razón y proporción. Escalas; repartos proporcionales;
porcentajes.
Rectángulos notables. El problema armónico: la
proporción del rectángulo. Proporcionalidad
inconmensurable estática. Proporcionalidad
inconmensurable dinámica: número de oro o áureo;
número de plata; proporcionalidad cordobesa.
2014
1
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
Proporcionalidad, arte, rectángulos notables y razones numéricas
Actividad 1
1- a)Realizar un poster que publicite la Fiesta Nacional de la Manzana (FNM), en hoja A3 y contenga:
 El logo de la fiesta actual o algún otro utilizado en años anteriores.
 El logo de la municipalidad de General Roca.
 Un texto publicitario que haya sido utilizado en la edición 2014
Nota: investigar logos utilizados en la FNM
b) Dibujar, en una hoja tamaño A4, un prototipo del poster anterior utilizando una escala
conveniente.
c) Indicar, en el prototipo tamaño A4, las medidas reales de los rectángulos correspondientes a los dos
logos.
d) ¿Qué % de la hoja A3 representa la hoja A4? Y de la hoja A2?
e) ¿Si se quisiera reducir el prototipo en tamaño A4 en 20%, cuáles serían sus nuevas dimensiones?
d) Supongamos que se quisieran imprimir 200 posters como el diseñado en a) en un centro de copiado
cuyas tarifas son: costo del m2 de impresión: $ 48.- y descuento del 8% para los trabajos que superen
los $800.- ¿Cuánto se pagaría por la impresión de los 200 posters?
2- El Municipio de General Roca contrata, todos los años, a una empresa de la ciudad para fotografiar
todo lo importante que ocurra durante la Fiesta Nacional de la Manzana (desde la elección de las
reinas hasta el momento de cierre de la Fiesta, incluyendo todos los stands que se presenten en el
predio de exposición). Dicha empresa cuenta con las siguientes medidas en fotos y papel que utiliza
para las mismas:
Medidas de las fotos
10cm x 15cm
Opción 1
13cm x 18cm
Opción 2
15cm x 21cm
Opción 3
Papel que utilizan las máquinas
156m x 12,7cm
Tipo a
186m x 15cm
Tipo b
a) ¿Cuántas fotos de cada opción se pueden imprimir si se utiliza el tipo de papel a? ¿y si se utiliza el tipo
de papel b?
b) ¿Con cuál o cuáles de las opciones de medidas para fotos se desperdicia menos papel, según sea el
tipo de papel?
c) Los dueños de la casa fotográfica quieren imprimir postales con imágenes de General Roca para
vender a los turistas. Si las dimensiones de las postales digitales que elaboran son de 13 cm x 19 cm
¿Cuál de los tipos de papel les conviene usar? ¿Por qué?
3- Consideremos ahora, la tarea del equipo de promoción de la Fiesta Nacional de la Manzana que está
pensando en la fabricación de vasos plásticos con el logo de la Fiesta para regalar a las autoridades y a
las reinas visitantes.
Para la confección de los vasos, el fabricante deberá cumplir con que toda la superficie del vaso sea cubierta
con un calco adhesivo con un logo, que se hará en formato A5.
2
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
a) Compara estos dos modelos de calcos posibles para el logo y decide cuál es el que se deberá
encargar a la imprenta si se quiere que el vaso tenga la máxima capacidad.
Para recordar
Long circ:
Área del circ:
Vol. Cilindro: Áreabase x altura
Figura N° 1
b) El dueño de una de las cantinas que estará en el predio de exposiciones, encargará a una fábrica de
plásticos la confección de vasos plásticos cilíndricos de 200 cm3 y 250 cm3 de capacidad para servir cerveza y
gaseosas. En dichos vasos se pegará un calco con el logo de la cantina. ¿Qué dimensiones podrían tener esos
vasos? ¿De qué dimensiones podrían ser los calcos para que puedan pegarse en cualquiera de los vasos?
Actividad 2
En la actividad 1 trabajaron con hojas de distintos tamaños de la serie A. Si las medidas de sus
dimensiones son respectivamente a y b; siendo b>a y cortamos por la mitad del lado mayor, obtenemos
un rectángulo de dimensiones a y b/2.
Reiterando la operación obtenemos un rectángulo b/2 y a/2. El rectángulo siguiente tendrá de
dimensiones b/4 y a/2 y así sucesivamente. Observamos que la relación entre el lado mayor y el menor es
siempre la misma, las hojas que obtenemos tienen la misma proporción y es próxima a
.
a. Organicen una tabla con las dimensiones de las hojas de la serie A, desde el tamaño A3 al A10 y
expliciten el factor de reducción que es necesario utilizar para pasar de un elemento a otro de la serie.
b. ¿Qué factor hay que utilizar para pasar de A4 a A6? ¿Y de A10 a A4?
c. Expliciten cómo pueden determinar el factor que es necesario utilizar para pasar de un formato a otro
cualquiera de la serie.
Rectángulos notables
En las civilizaciones antiguas se buscó la perfección de las formas en la relación de medidas que
vinculaban las distintas partes de la obra, cada parte con el total, el total con el formato-soporte e incluso las
del soporte en sí. Las relaciones de medida utilizadas por estas civilizaciones en general, guardaban cierta
“Proporción geométrica”.
Podemos distinguir dos tipos de proporción geométrica:
1- la que establece entre dos elementos una razón simple, expresable como dos múltiplos de una unidad ó
módulo: 2/3, 3/5, 1/2 (proporción estática)
2- la que relaciona dos valores por una razón inconmensurable, como
(proporción dinámica).
3
;
; π, razón áurea, etc.
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
La figura humana y las fachadas de edificios fueron dos temas clave en la aplicación de razones
proporcionales. Cuando no había fotografía había que construir la figura, y en este empeño tenemos ejemplos
de todo tipo:

Sistemas modulares, basados en la repetición de una unidad ó módulo: pinturas y relieves egipcios,
tratadistas como Arfe y Villafañe, Irala, etc. Figuras Nº 2, Nº3
Figura N° 3
Figura N° 2

Sistemas que establecen cada parte como una fracción de la altura: Vitrubio, Durero, Pacheco, y en
general todos los tratados que dividen la altura en 8 cabezas, 10 caras, 6 pies, etc. Figuras Nº 4 y 5
Figura N° 4

Figura N° 5
Esquemas simbólicos, de adaptación a formas geométricas: Villard de Honnecourt, Bizancio, canon
Varrónico. Figuras Nº 6 y 7
Figura N° 6
Figura N° 7
4
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
 Sistemas de analogías y equivalencias en la estructura: cánones griegos, antropometría
moderna. Figuras Nº8 y N°9
Figura N° 8

Figura N° 9
Aplicación de la razón áurea: da Vinci, Zeising, Theodore Cook, Le Corbusier.
Figuras Nº 10 y 11
Figura N° 10
Figura N° 11
En fotografía, donde el modelo no se construye, sino que se capta a partir de cierto punto de vista, bajo
cierto ángulo y encuadre, y donde el resultado suele ser una imagen contenida en un espacio rectangular, nos
interesa entender la proporción del formato. El cuadrado representa la unidad. Tiene mucha fuerza visual,
pero es la forma rectangular más estática. En el resto de los rectángulos domina el ancho ó el alto, así que
participan de las propiedades expresivas de la dirección horizontal y de la vertical.
Por ejemplo la horizontal es considerada como la dimensión del tiempo, de la constancia, de la
estabilidad, de la pasividad, los formatos apaisados refuerzan en los paisajes la sensación de placidez, de
intemporalidad, mientras que los verticales pueden subrayar temas más activos y comunicativos, como el
retrato, la figura ó el movimiento vertical de por ejemplo una cascada.
Razón o Proporción de un rectángulo
Se denomina proporción de un rectángulo ( Figura Nº 12 ) a la razón
expresada por sus lados, considerando que el numerador de la fracción sea el
Figura N° 12
mayor de los lados del polígono:
p(a;b)= .
Siempre p
5
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
Razones simples o conmensurables y rectángulos estáticos
Los pitagóricos y el platonismo en general estudiaron exhaustivamente las razones estáticas cuando
matemática y geometría estaban en pañales. Vincularon estas razones a los intervalos consonantes en música,
donde el unísono es la razón 1:1, la octava 1:2, la quinta (do-sol) 2:3, la cuarta (do-fa) 3:4, la tercera mayor
(do-mi) 4:5.
En la fotografía los fotogramas de un negativo de 35 mm son rectángulos estáticos, de formato que
son idóneos para imprimir copias de 15x10 cm. Los suministros de papel se hacen con mentalidad
rigurosamente estática, los cortes son siempre en múltiplos de 5 cm., con excepciones como el formato 13x18
cm.
Los formatos modulares ó estáticos nos resultan cómodos perceptivamente. Están basados en
razones aritméticas simples como por ejemplo: Figura Nº 13
Figura N° 13
Razones inconmensurables y rectángulos dinámicos
Nos referimos a las razones de tipo
y otras razones como el número de oro. Los rectángulos de
esta proporción forman una serie autogenerable. Estos rectángulos son los únicos que se pueden obtener
como reunión de “n” veces el rectángulo recíproco, es decir, dividiendo estos rectángulos en n partes por el
lado mayor, se obtienen n rectángulos de idéntica proporción al dado.
Algunos rectángulos dinámicos interesantes son: el rectángulo
, que se obtiene abatiendo la
diagonal de un cuadrado (Figura Nº 14-a), el rectángulo
(Figura Nº 14-b) que se inscribe en un hexágono
regular, ó el rectángulo áureo, que se obtiene abatiendo la "diagonal" de la mitad del cuadrado (Figura Nº 14c):
Figura N° 14
El rectángulo
o Rectángulo armónico o Rectángulo diagonal
Existen numerosos trazados geométricos que ayudan a generar armonía y coherencia, pero de todos
ellos, el que ha cobrado mayor relevancia es el que procede de lo que se conoce como “proporción
armónica”, conocida desde la época de las Pirámides pero que alcanzó su más alto grado de sofisticación y
refinamiento en la pintura y la arquitectura del Renacimiento Florentino.
La proporción armónica se basa en las propiedades de la diagonal del cuadrado; es decir, en las
relaciones existentes entre los lados de un cuadrado y su diagonal.
6
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
En otras palabras, proporcionar armónicamente implica proporcionar en base al cuadrado y su
diagonal. En un cuadrado de lado igual a 1 a diagonal vale
es el número
. Por lo tanto la base de las relaciones armónicas
.
Figura N° 15
El rectángulo
o rectángulo armónico es importante a nivel práctico porque resuelve el problema
de la duplicación manteniendo las proporciones. Si dividimos un cuadrado en dos rectángulos iguales, está
claro que éstas ya no mantienen la forma cuadrada. Esto se repite en cualquier rectángulo estético.
Pero si esto lo hacemos en un rectángulo armónico las dos mitades mantienen la proporción
.
La serie DIN-A, como ya se ha visto antes, ha normalizado los formatos de papel a partir de un
rectángulo de un metro cuadrado de superficie con sus lados en proporción 1 a raíz de 2, que es el formato A0. Su mitad es el formato A-1, la mitad de éste es el A-2, la mitad de éste A-3, y así con el A-4 que sustituye los
tradicionales formatos arbitrarios de folio, el A-5 que sustituye la cuartilla, el A-6 la octavilla, etc. etc. Figura
Nº 16
Figura N° 16
El formato es el que permite ampliar al doble de superficie en una fotocopiadora un documento sin
tener que hacer ajustes ni recortes, por eso en las máquinas siempre están los valores de
141% y 71%.
y su inverso:
Si realizamos el procedimiento anterior de división, podemos verificar que las hojas obtenidas, de tamaños
A0; A1; A2;….. etc. Se pueden ampliar así:
Figura N° 17
Figura N° 18
Analizando las Figura
A partir de las figuras Nº 17 y 18 concluimos que:
- los vértices superiores de las hojas quedan alineados
- las diagonales de todas las hojas se pueden superponer
Esta disposición se logra porque los rectángulos son semejantes, es decir, hay proporcionalidad entre los lados
respectivos
7
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
El rectángulo áureo
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
Tal vez la proporción más apreciada a lo largo de la historia ha sido la llamada proporción áurea, también
conocida como proporción divina. Esta proporción es la que permite dividir un segmento (Figura Nº20) de
manera que la parte menor y la mayor estén en proporción con la mayor y el total, es decir:
Los segmentos a y b (Figura Nº 20) resultan ser los lados de un rectángulo áureo (Figura Nº 19)
A la razón que define la proporción divina (a:b en este caso) se le llama el número
representa por la letra griega ɸ (se lee "fi").
Figura N° 20
de oro y se
Figura N° 19
Para obtener el valor numérico de ɸ tomemos b = 1, el valor de a corresponderá con la razón áurea (a/b). La
igualdad anterior se convierte en la ecuación:
a2- a -1=0 Resolviendo esta ecuación de segundo grado obtenemos dos valores:
a1 =1,6180339887498948482045868343656…= ɸ
a2 = -0,6180339887498948482045868343656…
Solo el primer número, que es positivo, tiene sentido asociarlo con la longitud de un segmento, por eso es que
se elige esta solución y es el número que se conoce como ɸ.
El número de oro es un número irracional y equivale, aproximadamente, a:
ɸ =1.618=
.
También el número áureo aparece en la relación entre los lados del
rectángulo de la Figura N º21, que se construye a partir de un
cuadrado de lado unitario.
La proporción de este rectángulo es: P(……….;……..)=
Figura N° 21
8
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Actividad 3
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
Determinación del punto que divide un segmento AB en dos partes en proporción áurea
Dibujar un segmento AB (de cualquier longitud)
 Se prolonga la recta a partir del extremo B.
 Se construye una perpendicular a AB desde el punto B.
 Se encuentra el punto medio C del segmento AB.
 Con radio BC y centro en B, se corta en D la perpendicular trazada desde el punto B.
 Se traza la recta AD.
 Con el mismo radio BD y con centro en D se corta la recta AD en el punto E.
 Con radio AE y centro en A se corta el segmento AB en el punto F.

El punto F determina la proporción áurea del segmento AB de manera que FB/AF = AF/AB.
La proporción áurea está presente en distintas manifestaciones humanas
La proporción áurea es un concepto sin el cual resulta difícil comprender la evolución del arte, la
arquitectura y la geometría. Los griegos encontraron que el número ɸ aparece con mucha frecuencia en
la naturaleza de ahí que, en su afán por reflejar la perfección y la armonía en ella, uno de los principios
centrales de su estética fuese encontrar relaciones espaciales que reprodujeran esta proporción.
Es por ello que en una gran cantidad de pinturas, objetos de cerámica o metálicos, esculturas, construcciones
se puede apreciar que han sido concebidos a partir de este principio estético
El uso de la proporción áurea produce una estilización de las figuras que busca la “belleza divina”. En las
imágenes de la Figura Nº 22 podemos observar dicha proporción áurea.
Figura N° 22
R. de la Hoz en su artículo "La proporción cordobesa" ilustra la proporción áurea:
“Euclides de Alejandría, trescientos años antes de Cristo, en el libro II de su tratado "Los Elementos", piedra
angular del edificio matemático, trata por primera vez de la "media y extrema razón", "proporción armónica",
"proporción áurea" o "regla de oro" ".
"La formulación euclidiana se limita a establecer que un rectángulo encierra la máxima belleza si resulta
semejante a otro formado por su lado mayor y la suma de ambos lados.”
Luca Pacioli escribe su tratado "La Divina Proporción" "llamada así por sus propiedades excelsas, supremas,
excelentísimas, incomprensibles, inestimables, innumerables, admirables, inefables, singulares..., que
corresponde por semejanza a Dios mismo".
Al descubrir estas propiedades se detiene en la decimotercera, número de comensales en la Santa Cena,
estimando que de seguir, equipararía la proporción divina al propio Dios y ello pondría en juego su salvación.
9
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
Entre las muchas propiedades que omitió para eludir el infierno, se encuentra la de que el rectángulo divino
tiene sus lados en la misma proporción que el radio y el lado del decágono.
Corolario obligado de la divinización de la proporción áurea es que la naturaleza, cuando es perfecta,
conforma a sus criaturas según la divina proporción.
También se construye un rectángulo áureo con el lado de un decágono y el radio de la circunferencia
circunscripta. Figura Nº 23
Figura N° 23
El hombre de Vitrubio de Leonardo Da Vinci trabajado en la 1º clase, (Figura Nº 25) ilustra claramente el
concepto de la divina proporción: en un cuerpo ideal la proporción áurea, es la existente entre la distancia del
plano umbilical a cabeza y pies. Nos encontramos ya abiertamente al hombre,
centro de la Creación, como canon de la divina armonía"
Figura N° 24
El arquitecto franco suizo Le Corbusier (1887-1965) también comentado en
esa 1º clase,fue un firme convencido de que la proporción áurea dominaba el cuerpo
humano y la Naturaleza concibió gran parte de su obra según esta proporción.
Inventó un aparato de medida conocido como Modulor , Figura Nº24,
basado en los rectángulos notables duplo y áureo, y en unas divisiones
proporcionales de sus lados que darían lugar a las famosas series Roja y Azul, ambas
sucesiones de Fibonacci.
Figura N° 25
10
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
En Pintura destacamos el Guernica (Figura Nº 26), de Picasso, de dimensiones 771 x 345 cm. y por
tanto de proporción es 2,2347.... Según el estudio de proporciones de Rudolf Arnheim : el cuadro se
descompone en un cuadrado central (lado 345 cm.) y dos rectángulos áureos laterales de 213 x 345 cm., por
tanto, el tablero se subdivide en un rectángulo áureo horizontal 558 x 345 cm. y otro vertical de 213 x 345 cm.
Aparecen otras divisiones armónicas sobre los lados relacionadas con el número de oro.
Figura N° 26
Ejemplos de rectángulos áureos los podemos encontrar, también en diferentes objetos de nuestra cultura, por
ejemplo en las tarjetas de crédito, en nuestro carnet de identidad y también en las cajitas de cigarrillos.
El rectángulo de plata
Un rectángulo de plata, es aquel cuya proporción es el número de plata:
1+
Está relacionado con el octógono regular (Figura Nº 28) ; en efecto, puede formarse un rectángulo de plata
con el lado del octógono y una de sus diagonales (la perpendicular al lado de apoyo del octógono.
Además puede generarse un octógono regular con la rotación de 45º de un rectángulo
de plata en torno a su centro.
Figura N° 27
11
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
Este rectángulo está formado por la yuxtaposición de un
cuadrado y del rectángulo dinámico en proporción
Figura Nº 28
.
d: diagonal del cuadrado de lado 1.
d
1+d=1+
Número de Plata
Figura N° 28
El rectángulo
En la Figura Nº29 se ha representado un rectángulo
a partir de un cuadrado de lado unitario.
Figura N° 29
También se forma este rectángulo a partir de un hexágono regular, siendo
sus lados una de las diagonales del hexágono y el lado del mismo del polígono. Figura Nº 30. Con este
rectángulo puede generarse, por rotación, el hexágono regular y su estrella 6/2.
Figura N° 30
El rectángulo enmarca una de las figuras más importantes de la Geometría Sagrada conocida como
“vesica piscis”. Figura N° 31
12
Carrera- Diseño de Interiores y Mobiliario-
Asignatura: MATEMÁTICA
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
En el proceso de geometrización característico del gótico, jugó un papel fundamental la traducción de
los Elementos de Euclides (siglo IV-III a. de C.). En la proposición primera del libro I, aparece la construcción de
un triángulo equilátero a partir de un segmento dado. De aquí se obtiene la “vesica piscis” (vejiga de pez)
llamada también mandorla.
Podemos definir la vesica piscis como la figura plana comprendida
entre dos arcos de circunferencia con centros en los puntos A y B de un
segmento dado AB, y radio la longitud del mismo, Figura Nº 28 Suponiendo
que la longitud del segmento AB es 1, la altura del triángulo equilátero ABC
mide
Figura N° 32
y por tanto la proporción del rectángulo circunscrito a la vesica es
.
Actividad 4
Los griegos que seguían las teorías de Pitágoras observaron que el número de oro se encontraba al relacionar
la diagonal y el lado de un pentágono regular.
a. Construyan una circunferencia de radio 3 cm, con un pentágono regular inscripto.
b. Determinen la razón entre cualquiera de sus diagonales y uno de sus lados. ¿Al cambiar la
longitud del radio de la circunferencia cambia el valor de dicha razón?
Actividad 5
El número
es irracional. Si lo calculan con la calculadora, obtendrán un valor aproximado, ya que
su expresión decimal tiene infinitos decimales, y la calculadora proporciona solo 8 ó 10. Veamos ahora una
forma de representar con precisión algunos irracionales al menos la forma ideal, ya que en la práctica factores
como el grosor del lápiz y errores inevitables de medición causan un resultado aproximado.
a- Dibujen un cuadrado sobre la recta numérica, haciendo coincidir un lado con el segmento con
extremos en 0 y 1. Tracen la diagonal que pasa por el 0.
Al hacer esta construcción, obtuvieron un triángulo con un lado sobre la recta numérica; ¿qué
clase de triángulo es teniendo en cuenta sus ángulos? ¿Cuánto mide la diagonal que
marcaron? ¿Por qué?
b- Tomen con el compás la medida de la diagonal y transporten sobre la recta numérica esta medida a
partir del 0. ¿Qué número irracional están representando?
c- Construyan sobre la recta un rectángulo de base igual al segmento que marcaron y altura de longitud
1 y vuelvan a trazar la diagonal que pasa por el 0 ¿Qué número pueden representar con esta
construcción?
d- Si el rectángulo que construyeron en el punto anterior tuviera altura de longitud 3, ¿cuál es el número
que podrían representar?
e- ¿Cómo representarían ?
Para conocer otras situaciones en las cuales aparece el número de oro, pueden visitar algunas de las
siguientes páginas web. http//rt000z8y.eresmas.net/El número
http//es.wikipedia.org/wiki/Número áureo
http//www.comenius.usach.cl/webmat2/proyectos/Numerodeoro.htm
http//gaussianos.blogsome.com/2006/10/03/la-proporcion-divina-el-numero-phi/
http//www.omerique.net/calcumat/numerooro.htm
http//gaussianos.com/la-proporción-divina-el-numero-phi/
13
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Actividad 6
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
Los diseños arquitectónicos y la belleza en las medidas
Muchos consideran que los rectángulos de sección de oro son más armoniosos y placenteros a la vista y el
número áureo aparece, en las proporciones que guardan edificios, esculturas, objetos, partes de nuestro
cuerpo...
¿Es posible afirmar que hay una proporción que sea más armoniosa que otra o que sea más “natural” para la
especie humana?
Para tener más elementos que permitan responder a esta pregunta analizaremos las proporciones presentes
en distintas construcciones.
a) El Partenón, (del griego Parthenos, virgen; uno de los adjetivos que servían de sobrenombre a Atenea)
, Figura Nº 33, es el templo griego situado en la Acrópolis de Atenas dedicado a Atenea Parthenos,
diosa protectora de la ciudad de Atenas. Es el monumento más importante de la civilización griega
antigua y se lo considera como una de las más bellas obras arquitectónicas de la humanidad. Es uno
de los principales templos dóricos que se conservan. Mide 69,5 x 31 m en planta y 18 metros de
altura. Su ancho y alto están en una proporción particular, que también se repite en todas las líneas
de construcción una y otra vez.
Figura N° 33
Fuente: www.ionlitio.com/category/arquitectura/
Sabías que:...
-…el arquitrabe del Partenón tiene un inclinación para que al mirarlo desde lejos no parezca
curvado hacia abajo.-…también las columnas tienen un ángulo de inclinación hacia el centro
para que no semejen estar hacia fuera.
-… la escalinata que lo rodea tiene escalones muy grandes, incómodos de subir caminando,
pero que están proporcionados con las dimensiones de todo el edificio. Para subir hay una
escalinata central con escalones más pequeños.
En la Figura Nº 33 comprueben, de manera aproximada, si
AB/CD = Φ,
AC/AD = Φ
y
14
CD/CA = Φ.
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
b) La Catedral de la Inmaculada Concepción se levanta frente a la plaza Moreno, en la manzana
comprendida por las calles 14 y 15 y los boulevares 51 y 53 de la ciudad de La Plata en la provincia de
Buenos Aires. Con ladrillo a la vista y por lo tanto inconfundible y bellamente rojiza, se ha convertido
en un símbolo característico de la ciudad. En el estilo neogótico es la más grande de América: su
superficie es de 7000 m2, tiene capacidad para 14.000 personas, mide 120 m de largo por 76 m de
frente, y la altura tomada hasta la cruz es de 97m. Fue inaugurada al público en 1932, cuando la
ciudad cumplía su cincuentenario.
La catedral neogótica platense fue inspirada en las catedrales góticas de Amiens (Francia) y de
Colonia (Alemania). Las medidas de la catedral platense son: largo interior 106 metros; ancho interior
del crucero, 67 metros, ancho de la nave mayor, 13 metros; ancho total de las naves laterales, 13
metros; sala de canónigos, 4,50 por 21 metros; altura de la bóveda de la nave mayor, 37 metros;
altura exterior de la linterna, 76 metros, interior 46 metros.
Determinen si en esta catedral algunas medidas están relacionadas o no con el número áureo.
Actividad 7
La ciudad de Córdoba, en España, muestra una rica mezcla de culturas ya que fue un centro urbano
importante del imperio romano y un centro comercial y cultural de muchísima importancia entre los siglos VII
y XIII al ser conquistada por los árabes. ¿También se encuentra la razón áurea en las construcciones
características de esta ciudad?
a) Lean el siguiente texto basado en un artículo del matemático y escultor Luis Ramos, sobre las
proporciones en la arquitectura, arte y escultura de Córdoba.
15
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
La proporción cordobesa
Trescientos años a.C. en el libro IIº de sus “Elementos de Geometría”, Euclides de Alejandría trata por
primera vez de la “media y extrema razón”, “proporción áurea”, “proporción armónica” o “regla de
oro”. Doce siglos después, sus “Elementos” fue traducida por Ishaq Ibin Iluncin, publicada por Alhazen
y estudiada en las escuelas de Córdoba. Esta ciudad fue depositaria del tesoro euclideano durante la
Edad Media, situación que cambió con una de las primeras acciones de espionaje científico de que se
tiene conocimiento.
En 1120, un británico adiestrado en el idioma, costumbres y disfrazado de estudiante hispanoárabe,
logró sacar una copia de “Los Elementos” que fue publicada en 1472. Hasta 1535 en que se descubre el
texto griego, el mundo no cuenta más que con esta traducción árabe; por lo que los trabajos de
Leonardo da Vinci y Luca Pacioli (decisivos para el Renacimiento), se hicieron a partir del texto
cordobés.
Era razonable pensar que en Córdoba las construcciones respetaran de la proporción áurea, sin
embargo esto no es así.
Refiriéndonos, en concreto a la cultura romana, y a ejemplos existentes en el museo arqueológico
local, encontramos que los cordobeses romanos autores de relieves, esculturas y mosaicos han
preferido proporcionar sus figuras humanas según la proporción 1,3.
Nos encontramos ante una nueva invariante en la arquitectura y el arte cordobés, la proporción 1,3 o
“canon cordobés”.
Figura N° 34
16
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
La división (razón o fracción) entre el radio de la circunferencia circunscrita y el lado del octógono
regular (Figura Nº 35) resultó ser un nº irracional que por redondeo es igual al determinado
empíricamente (en la práctica 1,3). De esta manera la proporción nacida de la realidad cordobesa
quedó instalada en la mística de los números, concretamente en el Nº 8 (en el octógono regular).
Figura N° 37
El octógono aparece en la Mezquita, el Mihrab, (Figura Nº 36) en varias torres, en muchas fuentes y
en otras construcciones de carácter religioso o civil.
También es notable que la pendiente que llegan a alcanzar los tejados es de 37º. Esta inclinación
coincide prácticamente con la de la diagonal de un rectángulo cordobés con el lado mayor como
base y se encuentra en las cubiertas de la Mezquita, en el tejado verde de la Catedral, y en Santa
Victoria el más alto de la ciudad.
Figura N° 37
En la Mezquita se plantea la arquitectura prefabricada, modular y crecedera, y este crecimiento
sigue unas líneas regidas por los rectángulos cordobeses.
Figura N° 37
La geometría de la fachada de Al-Hakam II y la fachada del Mihrat también se someten en su
estructura a la proporción cordobesa.
17
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
De la lectura del texto se puede concluir que históricamente en la arquitectura no sólo se ha trabajado
con el número de Oro, sino con otros irracionales.
b) Construyan un octógono regular y estableciendo la razón que se menciona en el texto; expresen
numéricamente el valor del número irracional que corresponde a la razón entre el radio de la circunferencia y
el lado del octógono.
Otros muchos edificios emplean en su composición la proporción cordobesa. Son muy numerosos los
edificios, incluso contemporáneos que están trazados con el rectángulo cordobés como base de
composición. No se sabe si los autores de estas obras las proporcionaron consciente o por puro
sentimiento. Lo que queda comprobado es que cuando una obra de arte cordobesa resulta bien
compuesta, encierra está determinada proporción. Y siendo esta proporción un hecho empírico frente a
la idealización de la proporción áurea, cabe la posibilidad de que su empleo haya surgido o se haya
extendido en otros pueblos de cultura y etnia afines a la cordobesa.
Fuente:
http://www.islamyal-andalus.org/control/noticia.php
02/2005
Figura N° 38
18
-
BOLETÍN
N°
36
-
Carrera- Diseño de Interiores y Mobiliario-
Asignatura: MATEMÁTICA
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
Problemas para aplicar los conceptos desarrollados y seguir practicando.
1- Durante el carnaval todos los medios gráficos envían fotógrafos para cubrir los desfiles de las distintas
agrupaciones y sus elegantes carrozas. Estas fotografías se amplían y reducen para adaptarse a los
formatos de las distintas publicaciones.
En un periódico escolar, los alumnos diagraman la portada para incluir la foto de una compañera que
desfila en una comparsa.
La foto a) de la Figura Nº39 es la original y las siguientes son reducciones que realizaron a través de la
computadora con el programa PAINT, utilizando la herramienta “expandir y contraer”, ¿cuáles de ellas
corresponden a una reducción proporcional a la original?
a)
b)
d)
c)
f)
e)
Figura N° 39
2- Mathilda, hábil espía de un lejano país, deja escondido en el hueco de una montaña un papel en el
que reprodujo la conversación que escuchó entre Loretto y Newton.
Cuando sus secuaces logran dar con el documento que contiene vital información, no pueden
descifrar lo que ha escrito Mathilda: el papel solo mide 2 cm de base por 3 cm de altura. Suponen que
si lo amplían de manera tal que las dimensiones lineales del papel aumenten 3/4, podrán leer su
contenido.
19
Asignatura: MATEMÁTICA
a)
b)
c)
d)
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
Cuando lo amplían, se dan cuenta de que aún es muy dificultoso leer lo escrito, por lo cual deciden
aumentar nuevamente 3/4 las dimensiones lineales de la ampliación. Hecho esto, logran descifrar la
información.
Dado un rectángulo de 2 cm por 3 cm, ¿podrían reproducir las ampliaciones que hicieron los secuaces
de Mathilda?
¿Cuáles fueron las dimensiones lineales luego de cada una de las ampliaciones?
¿Cuál es la proporción entre las dimensiones lineales de la primera ampliación y las dimensiones
lineales originales? ¿Y entre las dimensiones lineales de la primera ampliación y la segunda?
¿Es cierto que si se hubiera hecho la ampliación en un solo paso, las dimensiones finales
representarían 7/2 de las originales? ¿Por qué?¿Cuál sería el factor de ampliación aplicado en un solo
paso?
3- Dibujen un cuadrado sobre la recta numérica, haciendo coincidir un lado con el segmento con
extremos en 0 y 1. Tracen la diagonal que pasa por el 0.
a) Al hacer esta construcción, obtuvieron un triángulo con un lado sobre la recta numérica; ¿qué clase de
triángulo es teniendo en cuenta sus ángulos? ¿Cuánto mide la diagonal que marcaron? ¿Por qué?
b) Tomen con el compás la medida de la diagonal y transporten sobre la recta numérica esta medida a
partir del 0. ¿Qué número irracional están representando?
c) Construyan sobre la recta un rectángulo de base igual al segmento que marcaron y altura de longitud
1 y vuelvan a trazar la diagonal que pasa por el 0 ¿Qué número pueden representar con esta
construcción?
d) Si el rectángulo que construyeron en el punto anterior tuviera altura de longitud 3, ¿cuál es el número
que podrían representar?
4- Los amigos de Marcos encontraron unas fotos viejas, cuadradas y pequeñas de 10 x 10 cm, ideales
para decorar el salón de su fiesta de cumpleaños con cartulinas (44 x63 )cm .
a) Analizar el tipo de ampliación más conveniente para que quepa una foto por cartulina.
b) Si las fotos originales midieran (130x180)mm, y decidieran utiliza 2 por afiche (105x157)cm
¿Qué ampliación convendría más?
5- Miguel encontró una fotografía de 4 cm x 2 cm, y quiere ampliarla de modo tal que el lado que mide 4
cm pase a medir 7 cm.
a. ¿Cuánto debe medir el otro lado?
b. ¿Qué relación hay entre el área de la fotografía y el de la ampliación?¿Qué tiene que ver con la
relación entre los lados?¿Y con la relación entre los perímetros?
6- Si sacamos una fotocopia del plano de una habitación cuyo original mide 9 unidades de largo y 4
unidades de ancho con una reducción del 50%,
a. ¿qué dimensiones se reducen a la mitad: el largo, el ancho o el área? ¿Por qué?
b. Calcular el área de la habitación en el original y en la reducción.
c. Comparar las relaciones entre las áreas y entre los perímetros.
7- Se dispone de un mapa de la República Argentina en el que está indicada la escala, y de una fotocopia
de una de las provincias, ampliada al doble de sus longitudes.
Se marcan en la fotocopia de la provincia dos ciudades que están aproximadamente a 100 km una de otra,
resultando que están a 5 cm en la fotocopia.
a. En el mapa de la República Argentina, ¿a cuántos centímetros están una de otra?
b. ¿Cuál es la escala que corresponde a la fotocopia?
c. ¿Cuál es la escala del mapa?
20
Asignatura: MATEMÁTICA
Carrera- Diseño de Interiores y Mobiliario-
Prof. Alicia Iturbe– Prof. Cecilia Ariagno
d. Si el mapa de la provincia se ampliara de modo tal que su área fuera el doble, ¿cuál sería la
distancia entre las ciudades?
8a. Cuando sacamos una fotocopia aumentada al doble de un mapa cuya escala es 1:10000000, la escala
de la fotocopia es (justificar):
i.
1:10000000
ii.
1:20000000
iii.
1:5000000
b. Analizar si son verdaderas o falsas las siguientes afirmaciones y justificar:
i.
Si la escala de un mapa de la República Argentina es 1:100, y el camino desde Buenos Aires
hasta Córdoba mide sobre el mapa 8cm ± 0.5 cm, la distancia aproximada entre Buenos Aires
y Córdoba es de 800 km.
ii.
Si la distancia aproximada entre Buenos Aires y Córdoba es de 800 km y el camino desde
Buenos Aires hasta Córdoba mide sobre el mapa 8 cm ± 0.5 cm, la escala del mapa es
1:100000.
iii.
Si la distancia aproximada entre Buenos Aires y Córdoba es de 800 km y el camino desde
Buenos Aires hasta Córdoba mide sobre el mapa 8cm ± 0.5 cm, la escala del mapa es
1:10000000.
iv.
Cuando duplicamos la medida de los lados de un rectángulo, sus diagonales aumentan al
doble.
v.
Cuando duplicamos la medida de los lados de un rectángulo, sus diagonales aumentan al
cuádruple.
vi.
Cuando duplicamos la medida de los lados de un rectángulo, su área aumenta al doble.
vii.
Cuando duplicamos la medida de los lados de un rectángulo, su área aumenta al cuádruple.
21