elasticidad puntual precio de la demanda y sus
Anuncio

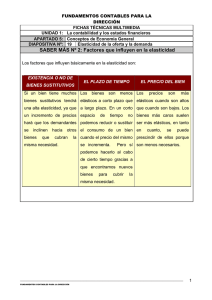
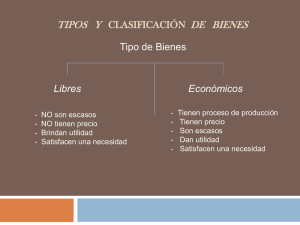
Página 1 de 6. ELASTICIDAD PUNTUAL PRECIO DE LA DEMANDA Y SUS APLICACIONES Jorge Isauro Rionda Ramírez1 SUMARIO: el presente trabajo plantea, más allá de las acepciones tradicionales de la elasticidad, usos alternativos para el manejo de relaciones de volúmenes de venta y precios de venta, cuyas proporciones estén libres de afectar bien las ganancias de las empresas, o bien sus cargas fiscales, entre otras aplicaciones. ABSTRACT: the present work outlines, beyond the traditional meanings of the elasticity, alternative uses for the handling of relationships of sale volumes and sale prices whose proportions are free of affecting the earnings of the companies well, or their fiscal loads, among other applications. Palabras clave: 1. Elasticidad 2. Precio 3. Volumen de venta PREÁMBULO: Sobre la elasticidad puntual precio de la demanda se ha dicho mucho. Todos los libros de economía, microeconomía y mercadotecnia la citan. El concepto es elemental. Más no obstante las aplicaciones son diversas, especialmente cuando se re expresa la relación como no lineal para un valor constante en cualquiera de la relación precio – cantidad de ventas, lo que le da una nueva dimensión en cuanto sus posibilidades de uso. El presente trabajo pretende precisamente aportar los posibles usos de este concepto para aplicaciones tales como el manejo fiscal de los lotes de venta y sus precios de venta cuando se desea que el nivel de ingreso neto permanezca constante, o bien que exista la liberad de establecer relaciones entre volumen por lote y precio sin verse afectada la carga fiscal de las empresa. 1 Profesor titular “A” tiempo completo de la Universidad de Guanajuato. Investigador de la Universidad De La Salle Bajío. Miembro del Sistema Nacional de Investigadores (nivel 1) CONACYT. Profesor de postgrado de la Universidad Internacional de Andalucía (España). Director de la revista electrónica Tecsistécatl (Universidad de Málaga). Página 2 de 6. LA ELASTICIDAD. El concepto económico de elasticidad se refiere al cambio que una variable dependiente sufre a efecto de un cambio en otra variable independiente. Normalizado matemáticamente en porcentaje, se trata de la cuantificación de dichos cambios en una expresión porcentual. Con ello, se puede estimar en el corto plazo cómo una variable afecta a otra, como por otra parte, dado el valor absoluto de la elasticidad |E| sea nayor (>), menor (<) o igual (=) a 1, se puede establecer una política relativa a un ratio que derive de la razón lógica entre las variables implicadas en el modelo. Si el modelo es lineal, de corto plazo, y las variables de interés son la cantidad demanda de un bien (Q) y el precio del propio bien (P), la relación lógica cualitativamente hablando se expresa como Q = f(P). De forma que linealmente el modelo queda como Q = a + bP, siendo Q la variable dependiente y P la variable independiente, y “a” la constante ordenada al origen y “b” la pendiente. La elasticidad entonces se mide como el cambio porcentual en la cantidad demandada debida a un cambio porcentual en el precio, de la forma: Cambio % en Q E = ------------------- = (dQ/dP)(P/Q) Cambio % en P Dos consideraciones importantes: Primero, al poner a Q como variable dependiente de P es inverso a como usualmente se expresa. En una gráfica como ordenada al origen se pone a Q, mientras que como abcisa aparece P. La pendiente dQ/dP es propiamente la pendiente de la curva de demanda. Si por lo contrario, P es variable dependiente de Q, la pendiente dQ/dP es el recíproco de la pendiente de la curva de demanda. Segundo, siendo la elasticidad E una línea de inversa proporcionalidad, la pendiente dQ/dP siempre será un valor negativo, mientras que la razón P/Q es siempre positiva. Por lo que menos por más, da menos. La elasticidad siempre será negativa. Los economistas comúnmente consideran el valor absoluto de la elasticidad como juicio de cambio. Siendo P variable independiente la función demanda queda como Q = a + bP Contrario, siendo P variable dependiente la demanda es P = a/b – Q/b. Partiendo de considerar a P como variable independiente, la pendiente de la función demanda (b) es negativa (tratándose de bienes normales). Por lo que otra expresión de la elasticidad es: Página 3 de 6. E = -bP/Q siendo que si b, P y Q son valores mayores a cero (>0) la elasticidad siempre es negativa. Considerando el valor como absoluto, entonces la elasticidad queda como: E = bP/Q Dado que la razón P/Q es diferente para cada punto de la curva Q = a + bP, la elasticidad es distinta para cada punto de la curva. (véase gráfica 5.1). GRÁFICA 5.1: Considérese que aquí el valor de la elasticidad es absoluto. Entre mayor sea el precio la elasticidad es tiende a infinito, entre menor sea el precio la elasticidad tiende a cero. La elasticidad puntual precio de la demanda como una función lineal es distinta para cada punto. A veces es conveniente manejar una función no lineal, de tipo potencia, para establecer como una constante la elasticidad (Browning y Zupan, 2003; 687-688)2. Del tipo siguiente: Q = aP-b donde “a” y “b” son constantes mayores a cero (a > 0 y b > 0). Con lo que se tiene que al estimar la demanda como función potencia, en cada punto la elasticidad es constante, de la forma como lo expresa la gráfica 5.2: 2 Browning, Edgar H. y Zupan, Mark A. (2003) Microeconomía, teoría y aplicaciones. CECSA. México. P. 722. Página 4 de 6. GRÁFICA 5.2: La comprobación de esto se obtiene de sacar la primera derivada de la función potencia: Q = aP-b dQ/dP = -baP-b-1 Siendo que la elasticidad puntual precio de la demanda se compone de este término: (dQ/dP)(P/Q) entonces E = -baP-b-1(P/Q) = (- baP-b)/Q = -b siendo que Q = aP-b Con ello se sabe entonces que E = b, que es un valor constante en cada punto de la función. Ahora bien, qué tan útil es tener esta información. Digamos, cuando se desea una razón de precios y ventas en una empresa donde el nivel de ingreso no se vea afectado, se tiene que E = b = 1. Así, el respectivo despeje de términos garantiza que la relación de precios y ventas obtenida no afecta el nivel de ingreso. Esto es útil cuando se maneja cargas fiscales que no se desean afectar vía ISR. O bien, cuando la empresa desea mantener una conducta de mercado que no sea afectada por la razón de precios y ventas por consideraciones financieras, digamos, con base al mejor manejo de los pasivos empresariales comprometidos respecto a los ingresos de la empresa. Asimismo, cuando se desea establecer, bien una escala productiva o una política de precios para el mejor manejo de los costos sin que afecte la cuestión de ingresos, fiscales y financieros. Mantener un valor de elasticidad de la demanda como elástica (|E|>1), unitaria (|E|=1) o inelástica (|E|<1), también sirve para establecer si los impuestos se cargan hacia delante (a consumidor) o hacia atrás (al proveedor), en una programación fiscal. Página 5 de 6. Ahora bien, si regresamos a la relación linea de Q = a + bQ, se tiene que el cambio en el precio viene a afectar el monto del ingreso total de la empresa. Respecto a la relación del Ingreso total (It) de la empresa, definida como It = P x Q, se obtiene la derivada de: dIt/dP = Q + P(dQ/dP) usando la regla de la cadena, = Q + P(dQ/dP) = Q[1+(P/Q)(dQ/dP)] = Q(1 – E) Cuando |E| = 1 la dIt/dP = 0 por lo que los cambios en el precio no afecta el It (gráfica 5.3). Cuando |E| > 1 la dIt/dP < 0 por lo que un aumento en P produce caiga el It. (gráfica 5.3). Cuando |E| < 1 la dIt/dP > 0 por lo que un aumento en P produce aumente el It. (gráfica 5.3). GRÁFICA 5.3: Los usos de saber esto es con respecto al criterio empresarial al tratar de manejar criterios del máximo beneficio y su estipulación entre el precio y la escala de producción (Q), bajo la condición de un mercado libre donde dicha escala lo determina el criterio donde el Ingreso marginal se iguala al costo marginal, o bien, en un mercado intervenido donde el precio y la cantidad lo determina la escala de producción donde coinciden el Ingreso medio con el costo marginal de la empresa. Asimismo, la elasticidad permite evaluar la política de precios y según el tipo de elasticidad las políticas financieras como fiscales serán distintas. Página 6 de 6. CONCLUSIÓN: La elasticidad puntual precio de la demanda, más que un indicador normalizado del cambio en el volumen de ventas a efecto de un cambio en la razón de precios de los bienes, por otra parte, en su re expresión como función no lineal permite estipular relaciones de volumen de ventas y razones de precios donde la elasticidad sea una constante, por lo que con ello bien se pueden establecer escalas de volúmenes de venta a diversos precios sin que se afecte el monto de beneficios de la empresa, de ingresos (brutos o netos), o las cargas fiscales. Lo que resulta una aplicación no solo novedosa de la elasticidad, sino en sí un recurso valioso para la política de precios y ventas en cuanto paquetes de mercadotecnia de las empresas que cuidan intereses de actuar sin que la razón de precios y volúmenes de ventas les afecten en ciertas variables que desean permanezcan como constantes. FUENTES BIBLIOGRÁFICAS: Browning, Edgar H. y Zupan, Mark A. (2003) Microeconomía, teoría y aplicaciones. CECSA. México. P. 722.