Document

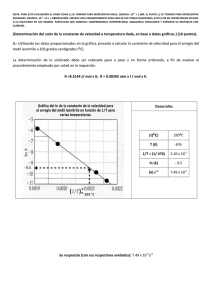
Unidad IV: Propiedades
fundamentales de la materia.
Facultad de Ingeniería
2012
UPV
Unidad IV: Propiedades
fundamentales de la materia:
•
•
Masa y densidad
– Concepto de masa
– Relación entre masa y volumen
– Concepto de densidad y peso especifico
– Propiedades de los compuestos
Temperatura y Dilatación
– Concepto de temperatura
– Escalas de temperatura y conversión
– Propiedades térmicas de la materia
• Propiedades térmica de los gases
– Expansión y compresión de gases
– Ley de los gases ideales
• Propiedades térmicas de los sólidos
– Dilatación lineal
– Dilatación superficial y volumétrica
La Materia
• La materia esta formada por átomos y estos
están constituidos por un núcleo y electrones
que giran alrededor.
• El núcleo esta compuesto por partículas
positivas llamadas Protones y partículas
neutras llamadas Neutrones
Masa Atómica
• La masa de un átomo esta concentrada en el
núcleo. Debido a lo pequeño que son los
átomos.
• La masa atómica es la masa que tiene una
sustancia elemental.
• Un átomo de hierro tiene una masa atómica
de 55,845 unidades de masa atómica (uma).
Cantidad de sustancia: Mol
• El mol (símbolo: mol) es la unidad con que se
mide la cantidad de sustancia y es una de las
siete magnitudes físicas fundamentales del SI.
• Dada cualquier sustancia ya sea, elemento o
compuesto químico y considerando a la vez un
mol de entidades elementales, donde estas
entidades elementales corresponde a
6,022·1023 unidades elementales.
Mol y Masa Molar
• Si tomamos 1 mol de átomos de hierro estos
masan 55,845 gramos. Por tanto se dice que la
Masa Molar de 55,845 g/mol.
• Podemos decir que 6,022·1023 átomos de
hierro masan 55,845 gramos
Masa
• La masa es la cantidad de materia de un
cuerpo.
• Es una propiedad intrínseca de los cuerpos
que determina la medida de la masa inercial y
de la masa gravitacional.
Masa
• La unidad utilizada para medir la masa en el
Sistema Internacional de Unidades es el
kilogramo (kg).
• Es una cantidad escalar y no debe confundirse
con el peso, que es una cantidad vectorial que
representa una fuerza.
Masa y Mol
• La masa de los compuestos esta relacionada a
través de la Masa molar por medio de la
siguiente expresión:
m
n
M
• Donde n es el número de moles, m masa en
gramos y M es la Masa molar.
Ejemplo 1. Para 0,325 moles de MgO,
determine:
a) Masa molar
b) Número de moléculas
c) Masa del compuesto.
Respuesta.
a) M = 24.305 g/mol + 15.999 g/mol= 40.304 g/mol
b) 0,325 moles ·6.022·1023=1.957·1023
c) n=m/M => m=n·M=0,325 mol· 40.304 g/mol
m= 13,0988 g
Masa
• La cantidad de materia se mide con balanza.
Densidad
Madera
masa
Densidad 
;
volumen
m
ρ 
V
Plomo: 11300 kg/m3
Madera: 500 kg/m3
2 kg, 4000 cm3
4000 cm3
177 cm3
Plomo
Mismo volumen
45.2 kg
Plomo
Misma masa
2 kg
Ejemplo 2: La densidad del acero es 7800 kg/m3.
¿Cuál es el volumen de un bloque de acero de 4 kg?
m
 ;
V
m
4 kg
V 
 7800 kg/m3
4 kg
V = 5.13 x 10-4 m3
¿Cuál es la masa si el volumen es 0.046 m3?
m  V  (7800 kg/m3 )(0.046 m3 );
m = 359 kg
Gravedad específica
La gravedad específica r de un material es la razón de
su densidad a la densidad del agua (1000 kg/m3).
r 
x
1000 kg/m3
Ejemplos:
Acero (7800 kg/m3)
Latón (8700 kg/m3)
Madera (500 kg/m3)
r = 7.80
r = 8.70
r = 0.500
Peso Especifico
El peso específico medio de un cuerpo, se
define como el cociente entre su peso P y su
volumen V.
masa·gravedad
Pe 
;
volumen
Unidades SI: Newton/m3
m·g
Pe 
V
Temperatura
La temperatura se relaciona con la actividad cinética de
las moléculas, mientras que la dilatación y los cambios
de fase de las sustancias se relacionan más con la
energía potencial.
Aunque no es cierto en todos los casos, un buen
principio es definir la temperatura como la energía
cinética promedio por molécula.
1
2
Ec  m·v
2
Energía Cinética
½mv

T
N
2
Temperatura contra energía interna
Misma
temperatur
a inicial
El volumen más
grande tiene
mayor energía
térmica
hielo
agua
hielo
Las jarras grande y
pequeña tienen la
misma temperatura,
pero no tienen la
misma energía térmica.
Una mayor cantidad de
agua caliente funde
más hielo.
Equilibrio de temperatura
Equilibrio térmico
Carbones
calientes
Agua fría
Contenedor
aislado
Misma Temperatura
El calor se define como la
transferencia de energía
térmica debido a una
diferencia en temperatura.
Dos objetos están en
equilibrio térmico si y sólo si
están a la misma
temperatura.
Termómetro
Un termómetro es
cualquier dispositivo que,
mediante escalas
marcadas, puede dar una
indicación de su propia
temperatura.
T = kX
X es propiedad termométrica: dilatación, resistencia
eléctrica, longitud de onda de luz, etc.
Escalas de temperatura
El punto fijo inferior es el
punto de congelación, la
temperatura a la que el hielo
y el agua coexisten a 1 atm de
presión:
1000C
0 0C
2120F
320F
0 0C o 32 0F
El punto fijo superior es el
punto ebullición, la
temperatura a la que vapor y
agua coexisten a 1 atm de
presión:
100 0C o 212 0F
Comparación de intervalos de temperatura
Intervalos de temperatura:
100 C0 = 180 F0
5 C0 = 9 F0
Si la temperatura cambia
de 79 0F a 70 0F, significa
una disminución de 5 C0.
1000C
2120F
100 C0
180 F0
tC
0 0C
tF
320F
Temperaturas específicas
Mismas temperaturas
tienen números
0F
diferentes: 0C
1000C
2120F
100 C0
180 F0
tC  00 tF  320

100 div 180 div
tC
tF
0 0C
320F
t  tF  32
0
9
5 C
tF  t  32
9
5 C
0
tC 
5
9
t
 32
0
F

Ejemplo 3: Un plato de comida se enfría de 1600F a
650F. ¿Cuál fue la temperatura inicial en grados Celsius?
¿Cuál es el cambio en temperatura en grados Celsius?
Convierta 160 0F a 0C de la
fórmula:
tC 
0
5
5(128
)
0
0
tC  (160  32 ) 
9
9
0
0


5
C
0
t  95 F 
0 
9F 
t
 32
0
F

tC = 71.1 0C
t  160 F  65 F  95 F
0
5
9
0
9 F0 = 5 C0
t = 52.8 C0
Limitaciones de las escalas relativas
El problema más serio con las escalas
Celsius y Fahrenheit es la existencia de
temperaturas negativas.
Claramente, ¡la energía cinética
promedio por molécula NO es
cero o en 0 0C o en 0 0F!
T = kX = ¿0?
¿-25 0C?
Termómetro a volumen constante
Presión
absoluta
Válvula
Volumen
constante de
un gas. (Aire,
por ejemplo)
La búsqueda para un
cero verdadero de
temperatura se puede
hacer con un
termómetro a volumen
constante.
Para volumen
constante:
T = kP
La presión varía con la temperatura.
Cero absoluto de temperatura
P1
P2
T1
T2
Cero absoluto
T
-2730C
0 0C
P
1000C
0 0C
1000C
Grafique los puntos (P1, 00C) y
(P2, 1000C); luego extrapole a
cero.
Cero absoluto = -2730C
Comparación de cuatro escalas
1000C
2120F
373 K
672 R
1 C0 = 1 K
460 R
5 C0 = 9 F
vapor
00C
320F
273 K
hielo
Celsius
K
Fahrenheit
C
Kelvin
F
R
Rankine
Cero
absoluto
-2730C
0K
-4600F
0R
tF  t  32
9
5 C

0
tC  95 tF  320
TK = tC + 2730

Propiedades térmicas de los gases
El comportamiento de los gases depende de la
Presión, Volumen, Temperatura y número de
moles.
La ecuación de los Gases ideales corresponde a un
modelo que predice las propiedades de los gases
que cumplen con los siguientes requisitos:
Las moléculas de gas ocupan un volumen casi nulo.
La energía cinética es muy alta.
Las moléculas de gas experimentan choques
perfectos.
Ecuación de los Gases Ideales
PV
·  n·RT
·
atm·L
R  0,082
K·mol
J
 8,3
K·mol
P  Presión
V  Volumen
n = número de moles
R = Constante de los gases
T = Temperatura Absoluta
Relación de Estados
• Es posible relacionar distintos estados para un
gas ideal por medio de la siguiente expresión:
P1·V1 P2·V2

n1T1 n2T2
• Si el numero de moles de gas permanece
constante, tenemos:
P1·V1 P2·V2
n1  n2 

T1
T2
Ejemplo 4: Un gas ideal ocupa un volumen de
100 cm3 a 20°C ya una presión de 100 Pa.
Determine el número de moles de gas en el
recipiente.
n=P·V/(R·T)
para este caso utilizaremos R=8,3 J/K·mol
n=100 Pa·0,0001 m3/(8,3 J/K·mol ·293K)
n=4,11·10-6 moles
Ejemplo 5: Se mantiene un gas ideal en un
recipiente a volumen constante. Inicialmente,
su temperatura es 100 ºC y su presión es 2,5
atmósferas ¿Cuál será la presión cuando la
temperatura sea de 80°C?
P1·V1 P2·V2

T1
T2
V1  V2
P2
2,5atm

373K
353K
P2  2,36atm
Dilatación lineal
L   L0 t
to
L

L0 t
Cobre:  = 1.7 x 10-5/C0
Hierro:  = 1.2 x 10-5/C0
Lo
L
L
t
Concreto:  = 0.9 x 10-5/C0
Aluminio:  = 2.4 x 10-5/C0
Ejemplo 2: Una tubería de cobre mide 90 m de largo
a 20 0C. ¿Cuál es nueva longitud cuando a través de la
tubería pasa vapor a 1000C?
Lo = 90 m, t0= 200C
t = 1000C - 200C = 80 C0
L = Lot = (1.7 x 10-5/C0)(90 m)(80 C0)
L = 0.122 m
L = Lo + L
L = 90 m + 0.122 m
L = 90.12 m
Aplicaciones de la dilatación
Hierro
Latón
Latón
Hierro
Junta de
dilatación
Tira bimetálica
Las juntas de dilatación son necesarias para permitir que
el concreto se dilate, y las tiras bimetálicas se pueden
usar como termostatos o para abrir y cerrar circuitos.
Dilatación de área
Dilatación al calentarse.
A0
A
La dilatación de área es análoga a la
ampliación de una fotografía.
El ejemplo muestra una tuerca caliente que se
encoge para un firme ajuste después de
enfriarse.
Cálculo de dilatación de área
A0 = L0W0 A = LW
L = L0 + L0 t W =
W0 + W0 t
W
W
L = L0(1 + t ) W =
W0(1 + t
A = LW = L0W0(1 + t)2
Wo
L
Lo
L
A = A0(1 + 2 t)
Dilatación de área: A = 2A0 t
Dilatación de volumen
La dilatación es la
misma en todas
direcciones (L, W y
H), por tanto:
V = bV0 t
b  3
La constante b es el coeficiente
de dilatación de volumen.
V
b
V0 t
Ejemplo 3. Un vaso de precipitados Pyrex de 200 cm3 se llena
hasta el tope con glicerina. Luego el sistema se caliente de 20
0C a 80 0C. ¿Cuánta glicerina se desborda del contenedor?
Glicerina: b  5.1 x 10-4/C0
200C
Pyrex: b = 3
b  30.3 x 10-5/C0) b
= 0.9 x 10-5/C0
Vdesb = VG - VP
Vdesb= ¿?
800C
V0
V
200 cm3
Vdesb = bGV0 t - bPV0 t = (bG - bP )V0 t
Vdesb = (5.1 x 10-4/C0- 0.9 x 10-5/C0)(200 cm3)(800C - 200C)
Ejemplo 3. (continuación)
Glicerina: b  5.1 x 10-4/C0
Pyrex: b = 3
b  30.3 x 10-5/C0)
b = 0.9 x 10-5/C0
Vdesb = VG - VP
200C
Vdesb= ¿?
800C
V0
V
200 cm3
Vdesb = bGV0 t - bPV0 t = (bG - bP )V0 t
Vdesb = (5.1 x 10-4/C0- 0.9 x 10-5/C0)(200 cm3)(800C - 200C)
Desbordamiento de volumen = 6.01 cm3