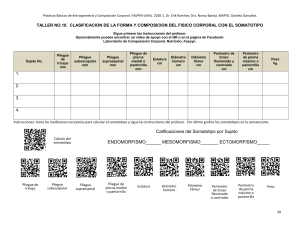
Matemáticas II Relación de ejercicios del tema 4: Aplicaciones
Anuncio

Matemáticas II
Relación de ejercicios del tema 4:
Aplicaciones lineales
1. Estudie cuáles de las siguientes transformaciones son aplicaciones lineales:
(a) f : R3 → R3 , f (x, y, z) = (x, y, z) = (a1 , a2 , a3 ) donde (a1 , a2 , a3 ) es un vector fijo de
R3 . Si no es siempre lineal, ¿existe algún vector (a1 , a2 , a3 ) para el que lo sea?
(b) f : R3 → R3 , f (x, y, z) = (a1 , a2 , a3 ) donde (a1 , a2 , a3 ) es un vector fijo de R3 . Si no
es siempre lineal, ¿existe algún vector (a1 , a2 , a3 ) para el que lo sea?
(c) f : R3 → R3 , f (x, y, z) = (x2 , 0, y + z)
(d) f : P3 (R) → P3 (R), f (p(x)) = xp0 (x)
(e) f : R2 → R2 , f (x, y) = (x + y, x)
(f) f : R2 → R2 , f (x, y) = (xy, x)
(g) f : R2 → R3 , f (x, y) = (x, y, x + y)
(h) f : R2 → R, f (x, y) = x2 y 2
(i) f : Mn (R) → Mn (R), f (A) = A − At
2. Sean las aplicaciones lineales f, g : R2 → R2 dadas por f (x, y) = (y, −x) y g(x, y) =
(x, −y). Determine f + g, f ◦ g y g ◦ f , y pruebe que las tres transformaciones anteriores
son también aplicaciones lineales.
3. ¿Existe una aplicación lineal f : R3 → R4 de forma que su núcleo sea el subespacio
generado por (1, 0, 1) y (1, 1, 1) y la imagen esté generada por (1, 0, 0, 0) y (1, 2, 0, 0)?
4. Determine el núcleo y la imagen de la aplicación lineal f : R3 → R3 definida por f (x, y, z) =
(2x + y + 4z, x + y + 2z, x + y + 3z).
5. Sea f : R4 → R4 el endomorfismo dado por:
f (a, b, c, d) = (a + 2b + c + 2d, 2a + 4b + 3c + 5d, 3a + 6b + 2c + 5d, a + 2b + c + 2d).
Determine su matriz asociada respecto a la base canónica de R4 y determine una base de
su núcleo y de su imagen.
6. Determine un endomorfismo f de R2 tal que f (2, 5) = (1, 3)y f (1, 3) = (1, −1).
7. En R3 se consideran los subespacios U = L((1, 1, 1)) y W = {(x, y, z) ∈ R3 : x+y +z = 0}.
Determine un endomorfismo f de R3 de forma que Ker(f ) = U e Im(f ) = W .
1
8. Sea f : R3 → R2 una aplicación lineal tal que f (1, 0, 0) = (−1, 0), f (0, 1, 0) = (2, 1)
y f (0, 0, 1) = (3, 3). Determine f , su matriz asociada respecto de las respectivas bases
canónicas de R3 y R2 y la dimensión y una base de su núcleo y de su imagen.
9. Considere el endomorfismo de R3 dado por f (0, 0, 1) = (0, 0, 1), f (1, −1, 0) = (1, −1, 0) y
f (1, 1, 0) = (0, 0, 0). Calcule la matriz asociada a f en la base canónica.
10. Considere el endomorfismo de R3 dado por f (1, 1, 1) = (2, 3, 3), f (1, 1, 0) = (1, 3, 2) y
f (1, 0, 0) = (0, 1, 1).
(a) Calcule la matriz de f respecto de la base canónica de R3 .
(b) Calcule la dimensión y una base del núcleo y de la imagen de f .
(c) Calcule la matriz del endomorfismo f respecto de la base B 0 = {(1, 1, 1), (1, 1, 0), (1, 0, 0)}.
2