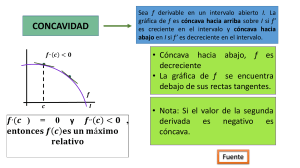
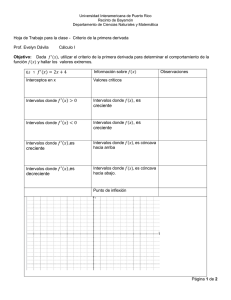
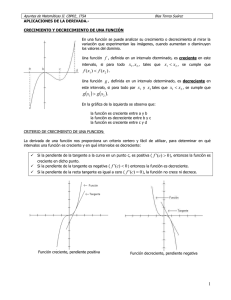
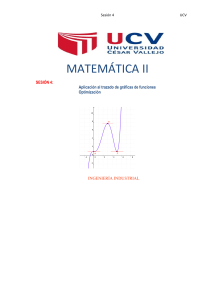
4 = + xfxx 1 + = xfxx 1 2 15. 12 = − + fxxx

Universidad de Puerto Rico
Recinto Universitario de Mayagüez
Departamento de Ciencias Matemáticas
Tercer Examen Departamental Mate 3031
30 de noviembre de 2010
Nombre__________________________. Número de estudiante____________________
Profesor__________________________
Sección_____________.
Instrucciones: En cada problema muestre todo el trabajo necesario para llegar a su
respuesta. Las soluciones presentadas sin trabajo podrían no recibir crédito. Respuestas
numéricas deben presentarse como expresiones matemáticas exactas, no mediante una
aproximación decimal. Use aproximaciones decimales sólo en casos en que las
instrucciones del problema específicamente las requiera.
I.
II.
(6 puntos)Encuentre todos los intervalos donde f ( x ) =
x2
es decreciente.
x2 + 4
x2 + 1
(6 puntos)Encuentre todos los intervalos donde f ( x ) =
es cóncava hacia
x2
arriba.
III.
(6 puntos)Encuentre todos los puntos de inflexión de f ( x ) =
1 4
x − 2 x 2 + 15.
12
2
 = f ' ( 0 ) = 0 y f " ( x ) = 6 x − 2 , determine dónde f tiene un
3
 
IV. (4 puntos)Dado f ' 
máximo local y dónde tiene un mínimo local o explique por qué no se puede
determinar.
V. (22puntos)Sea f ( x ) =
2x
( x + 4)
3
. Determine:
a. Dominio: __________________
b. Interceptos:
En eje de x: ________ , En el eje de y: ___________
c. Asíntota(s) horizontal(es):_____________________
d. Asíntota(s) vertical(es):_____________________
e. Primera derivada:___________________
f. Segunda derivada:___________________
g.
h.
i.
j.
Valores críticos: ______________________
Máximos locales:________________________
Mínimos locales: _______________________
Puntos de inflexión: _______________________
k. Intervalos donde f (x) es:
creciente: ______________________________
decreciente: ___________________________
l. Intervalos donde f (x) es:
cóncava hacia arriba: _______________________
cóncava hacia abajo: ___________________________
m. Use todos estos datos y puntos adicionales para dibujar la gráfica:
VI.
Considere
f ( x) =
1
2 − x2
a) (4 puntos)Encuentre la linealización de
f cerca de x = 1
b) (3 Puntos)Use la linealización obtenida en la parte a) para estimar el valor de
f (1.02)
VII.
Sea f ( x ) = e cos x
−x
0 ≤ x ≤ 2π .
a)(6 puntos) Encuentre los números críticos de
f.
Los números críticos son :_______________________
b) (5 puntos)Encuentre los valores máximos y mínimos absolutos de
VIII.
f.
A)(6 puntos) Considere la función f ( x ) = 4 + x − 1 en [1,5] . Verifique que se
satisfagan las hipótesis del Teorema del Valor Medio. Halle un número para el cual se
cumpla la conclusión del teorema.
B) (5 puntos) Sea f ( x ) =
1
. Demuestre que no hay ningún valor c en el intervalo
x2
( −2,1) de modo que f (1) − f ( −2 ) = 3 f ' ( c ) . Explique por qué esto NO
contradice el Teorema del Valor Medio.
IX.
A)(5 puntos) Encuentre lim
x→0
sin ( 5x )
x 2 + tan x
1 
 1
−

2
x4 
x
B)(6 puntos) Encuentre lim 
x →0
C) (6 puntos)Encuentre lim ( x + 1)
x →∞
2 x
IX.(10 puntos)Dibuje la gráfica de una función h que satisfaga las condiciones siguientes:
h ( −2 ) = 4
h ′(2) = h ′( − 2) = 0
h ( 0) = 2
h(2) = 1
h′( x) < 0 si − 2 < x < 2
h′′( x ) < 0 si
h′( x) > 0 si
x >2
x < 0.
h′′( x) > 0 si
x>0