B - Práctica de Cinemática

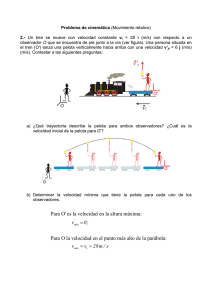
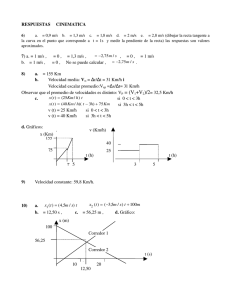
Taller de Enseñanza de Física
Curso 2010 - En su XXVI aniversario
Práctica de Cinemática
Problema 1
Objetivo: Utilizar los conceptos de posición, desplazamiento, trayectoria y distancia.
Un hombre da una vuelta a la manzana comenzando desde su casa que se encuentra en una esquina. Camina
inicialmente de Sur a Norte, volviendo nuevamente a su casa en 8 minutos. Vamos a analizar el movimiento del
hombre considerando que camina al mismo ritmo durante su viaje,
a) ¿Qué elegirías cómo objeto de estudio? ¿Por qué? ¿Cómo lo
modelizás?
b) Elegí un marco de referencia y ejes coordenados adecuados
para analizar la situación. ¿Cuántos ejes necesitaremos? ¿Por
qué?
c) Representá la trayectoria del hombre;
d) Identificá, en esa representación, la posición del hombre a los
2 minutos, a los 4 minutos, a los 6 minutos y a los 8 minutos;
e) Calculá su desplazamiento para los intervalos de tiempo de 0-2
minutos, 0 - 4 minutos, 4 - 6 minutos y 0 - 8 minutos;
f) ¿Qué distancia recorrió en cada uno de esos intervalos?
g) ¿Cuál es la longitud de la trayectoria recorrida?
h) Hacé gráficas de las componentes de la posición como
funciones del tiempo, considerando que el hombre:
i. camina siempre al mismo ritmo;
ii. camina al mismo ritmo los primeros 5 minutos, se detiene 1 minuto y reinicia la marcha al ritmo
inicial.
Problema 2
Objetivos: Intepretar gráficos y asociarlos con funciones.
Altura [cm]
Altura [cm]
Compará las siguientes gráficas de crecimiento. ¿Cambia la altura con el tiempo? ¿En qué unidades se mide
el cambio? ¿Cuáles gráficas representarían modelos de crecimiento de una planta?
Tiempo [días]
Altura [cm]
Altura [cm]
Tiempo [días]
Tiempo [días]
Tiempo [días]
Problema 3
Objetivo: Asociar a la velocidad con la pendiente de la recta en un gráfico (x,t). Vincular el gráfico (x,t) con la
función x(t).
El siguiente gráfico representa cuando Ema empezó a gatear al
cumplir 8 meses.
a) ¿Qué objeto de estudio describe el diagrama? ¿Cómo está
modelado?
b) ¿Dónde están el marco de referencia y el sistema de coordenadas
que corresponden a este diagrama?
c) ¿Qué distancia recorrió Ema entre los 0-3 segundos, 3-6 segundos, y
6-9 segundos?
d) ¿En qué tramo Ema se movió más rápido?
e) Escribí para cada tramo la expresión analítica para x(t) que
represente el cambio en la coordenada x de la posición como
función del tiempo.
X [m]
8
6
4
2
2
4
6
8
10
t [s]
Problema 4
Objetivo: Asociar velocidad y aceleración con derivada primera y segunda de la posición.
La figura muestra la variación de una coordenada
posición de un automóvil en función del tiempo en el tramo
recto de una ruta.
1. ¿Cuál es el objeto de estudio que representa la
gráfica? ¿Cómo está modelizado?
2. ¿En cuál de los instantes desde t0 a t7 es: a)
negativa la velocidad?; b) positiva la
velocidad?; c) nula la velocidad?; d) negativa la
aceleración?; e) positiva la aceleración?; f) nula
la aceleración?
3. ¿Podrías describir lo que sucede con el
automóvil desde t = 0 a t = t7? ¿Cuál es el
marco de referencia? ¿Dónde está ubicado el
origen de los ejes coordenados?
x
t0 t1
t2 t 3 t4
t5
t6
t7
t
Problema 5
Objetivo: Interpretar gráficas, distinguiendo posición de velocidad y aceleración.
Una piedra se lanza verticalmente hacia arriba.
a) Realiza un esquema de la situación. Grafica en dos instantes que elijas: la posición, velocidad y
aceleración de la piedra.
b) Seleccioná entre las gráficas siguientes la que nos muestra la componente de la posición de la piedra en
función del tiempo.
c) Seleccioná entre las gráficas siguientes la que nos muestra la componente de la velocidad de la piedra
en función del tiempo.
d) Seleccioná entre las gráficas siguientes la que nos muestra la componente de la aceleración de la piedra
en función del tiempo.
En cada caso, ubicá el sistema de coordenadas, el marco de referencia, identificá el objeto de estudio y cómo lo
modelás. Argumentá por qué no elegiste las otras gráficas.
e) Analizá qué marco de referencia y ejes coordenados están implícitos en las gráficas elegidas.
A
B
y
C
y
y
t
t
D
t
E
y
F
y
t
y
t
t
Problema 6
Objetivo: Interpretación de figuras asociadas a la Geología y que involucran conceptos físicos.
La siguiente imagen muestra los desplazamientos sufridos por distintos puntos de Sudamérica a partir del
terremoto ocurrido recientemente en Chile
a.
b.
c.
d.
¿Cuál es el objeto de estudio? ¿Cómo está modelado?
La imagen ¿Tiene algún marco de referencia y sistema de coordenadas implícito o explícito? ¿Cuál/es?
¿Podrías decir algo sobre la velocidad con la que se desplazaron los distintos puntos? ¿Por qué?
¿Qué podes decir sobre el largo de las flechas rojas y la relación entre ellas? ¿Se te ocurre alguna otra forma de
representar los desplazamientos?
Problema 7
Objetivo: Plantear funciones de movimiento.
Un esquiador comienza a descender por una ladera y aumenta su velocidad con una aceleración constante hasta
llegar, al cabo de 5 s, a la velocidad de 10 m/s. ¿Cuál es su aceleración?
Problema 8
Objetivos:
 Interpretar físicamente el enunciado.
 Aplicar los conceptos cinemáticos.
 Utilizar las representaciones gráficas y analíticas para resolver el problema.
 Interpretar físicamente el resultado calculado.
 Diferenciar los conceptos de posición y velocidad.
 “Leer” en un gráfico (x,t) a la velocidad como la derivada.
Siempre con problemas de puntualidad, Raúl corre por el andén con la intención de alcanzar el tren que acaba
de partir. En el instante en que el tren inicia su movimiento, Raúl se encuentra 30 m por detrás de la última puerta del
tren y corre con rapidez constante de 3,7 m/s. Cuando el tren arranca, la función que describe la evolución de la
componente X de la posición del tren con el tiempo es XTREN(t) = 0,1 m/s2 t2.
1. ¿Logrará Raúl su objetivo?
Para poder fundamentar tu respuesta te sugerimos que pienses en lo siguiente:
A. Hacé un esquema de la situación.
B. ¿Cuáles serán los objetos de estudio?¿Cómo los modelizarías?
C. ¿Dónde se encuentran el Marco de Referencia y el Sistema de Coordenadas implícito en la expresión
XTREN(t)?
D. ¿Cómo escribirías “matemáticamente”, la función XRAÚL(t) que describe la evolución de la componente X
de la posición de Raúl con el tiempo?
E. Graficá en un mismo gráfico (valga la redundancia) las funciones que describen la evolución con el
tiempo de la componente X de la posición del tren y de Raúl. ¿Hay algún modelo implícito en el
gráfico?¿Cuál?
F. ¿Podés ahora contestar la pregunta 1? ¿En qué instante/s Raúl puede subirse al tren?
2. Observando el gráfico anterior:
A. ¿Existe algún instante en que la posición de Raúl es la misma que la del tren? Identifícalo en el gráfico.
Calculá el valor numérico
B. ¿Existe algún instante en que la velocidad de Raúl es la misma que la del tren? Identifícalo en el gráfico.
C. ¿En qué momento/s la velocidad del tren es mayor que la de Raúl?
D. ¿En qué momento/s la velocidad de Raúl es mayor que la del tren?
Problema 9
Objetivos:
 Discutir cualitativamente la solución de un problema de encuentro.
 Distinguir entre velocidad y posición.
 Utilizar funciones que describen el movimiento, analizar su relación con marcos de referencia y
comparar la solución obtenida con el resultado cualitativo anterior.
 Identificar objeto de estudio, modelo, marco de referencia y ejes de coordenadas.
Dos automóviles (A y B) van por una ruta, uno delante del otro, ambos a velocidad constante. En determinado
momento, el automóvil que va detrás aumenta su velocidad y pasa al primero.
I) Sin hacer cuentas, ¿podrías decir si ambos automóviles tuvieron en algún momento la misma velocidad?
II) Si es así, ¿en qué momento sucede?
Considerá los siguientes casos:
a. vA = vB
b. vA  vB
c. vA < vB
y representá gráficamente la posición y la velocidad en función del tiempo de cada automóvil.
III) ¿Cómo podemos utilizar las siguientes funciones para resolver este problema?
1
𝑟 𝑡 = 𝑟0 + 𝑣0 𝑡 + 2 𝑎 𝑡 2
𝑣 𝑡 = 𝑣0 + 𝑎 𝑡
Problema 10
Objetivo: Aplicar herramientas de cinemática.
Una pelota es lanzada verticalmente hacia arriba desde la base de un edificio. Un vecino del quinto piso (a
17 m de altura), observa que la pelota se detiene frente a su ventana y vuelve a caer.
a) Determiná la velocidad con que fue lanzada la pelota.
b) Determiná el tiempo total en que la pelota estuvo en el aire.
c) Calculá el lapso que transcurrirá entre que la pelota pase por la ventana del tercer piso (11 m sobre el
nivel de la vereda), hacia arriba y hacia abajo.
d) Determiná las velocidades observadas desde la ventana del tercer piso, tanto cuando la pelota va hacia
arriba como cuando va hacia abajo.
Problema 11
Objetivo: Aplicar herramientas de cinemática.
Una liebre y una tortuga deben correr una carrera en un tramo recto de 0,5 km. Ambas empiezan a correr
en el mismo instante desde el punto de partida, llevando la liebre una rapidez inicial de 4 m/s y la tortuga de 1 m/s.
Tras correr durante 1 minuto a dichas velocidades, la liebre se detiene a dormir 7 minutos, confiada en la lentitud
de la tortuga. Al despertar, continúa la carrera a la misma velocidad inicial.
a) Graficá, en un mismo sistema de ejes, la posición de los dos animales en función del tiempo. Calcular:
b) ¿En qué instante aventaja la tortuga a la liebre?
c) ¿A qué distancia del punto de llegada está la liebre cuando la tortuga llega al final?
d) ¿Cuál es el tiempo máximo que podría haber dormido la liebre sin perder la carrera?
Problema 12
Un astronauta, divirtiéndose sobre el planeta Kryptón recientemente descubierto, lanza una pelota que sigue una
trayectoria parabólica tal como se muestra en la figura. La posición de la pelota está indicada, en la misma figura, a
intervalos de 1 segundo hasta t = 3 s. Para t = 1 s, la velocidad de la pelota está dada por
a) Determiná la velocidad de la pelota para t = 0 s, 2 s y 3 s.
b) ¿Cómo está orientado el sistema de coordenadas?
c) ¿Cuál es la aceleración de la gravedad en el planeta Kryptón?
Problema 13
Durante una batalla en altamar, una de los barcos comienza los cañonazos. Los cañones se encuentran a 2 m sobre
el nivel del mar y la bala recorre una curva cuya altura máxima es de 16 metros y, finalmente impacta sobre el mar
a una distancia horizontal de 46 metros del barco.
a) Graficá, en dos dimensiones, la trayectoria de la bala e indicá los vectores velocidad y aceleración en
algunos puntos de la misma.
b) Suponiendo despreciables los efectos aerodinámicos, describí el movimiento mediante funciones del
tiempo para cada componente de la posición y la velocidad. Grafícalas en función del tiempo.
c) Calculá las componentes de la velocidad inicial del lanzamiento.
Problema 14
Anastasio Weinberg, ya seguro de la solidez de sus conocimientos sobre el movimiento, decide dar un paso más:
quiere dar una expresión analítica al movimiento. Descubrió una plaza muy rara, donde hay una explanada grande
pero no horizontal, de la que mostramos un esquema de puño y letra de Anastasio, donde introdujo dos ejes de
coordenadas, que llamó "H" y "L":
Ahí probó patear su pelota de fútbol a ras del piso y encontró que, para uno de sus tiros, podía representar el
movimiento de esta manera:
H(t) = -6 m +5 m/s t – 0.7 m/s2 t2
L(t) = −1,5m + 1,25 m/s t
a. Discutan el diagrama de Anastasio hasta asegurarse de comprender su significado. De ser necesario hagan
sus propios diagramas.
b. Hagan un dibujo a escala de los ejes L y H, asegurándose de que la explanada cabe completa en él. Incluyan
la frontera de ésta.
c. Con lápiz y marcando suave grafiquen L versus tiempo y H versus tiempo desde el instante inicial hasta 8
segundos después siguiendo estos pasos: un miembro del grupo calcula H(0s), L(0s), H(1s), L(1s), H(2s),
L(2s) y los representa en gráfico H versus tiempo y L versus tiempo, y en el plano a escala; el segundo
miembro lo mismo para H(2s), L(2s), H(3s), L(3s), H(4s), L(4s); el tercero lo mismo para H(4s), L(4s), H(5s),
L(5s), H(6s), L(6s); el cuarto H(6s), L(6s), H(7s), L(7s), H(8s), L(8s), y el quinto puede hacer cualquier terna de
números para verificar las cuentas. Luego, como en la actividad anterior, reúnan el trabajo de todos para
dar lugar a las curvas de H y L versus t y a la trayectoria en el plano a escala.
d. Muestren sobre el esquema de Anastasio cómo fue el movimiento de la pelota. ¿Logran imaginarlo? ¿Es
más o menos como esperan que sea?
e. Las expresiones que dió Anastasio ¿Son válidas para todo valor de t? Discutan, ¡Y no se queden con ninguna
duda!
Problema 15
Objetivo agregado: Aplicar las herramientas de física y matemática a un problema de trascendencia patriótica.
A los 43 minutos del segundo tiempo del partido Argentina vs. Nigeria, se produce un tiro libre para la escuadra
albiceleste. El partido está 1 a 1 y El Apache Tevez pide el tiro libre. La barrera se sitúa a una distancia B de la
ubicación de la pelota y tiene su máxima altura h cuando salta Lumumba. Con su intuición física El Apache sabe
que, si consigue patear la pelota de manera tal que salga en una dirección inicial determinada por el ángulo α, la
pelota llega a la barrera con una altura de h + 5 cm, y resulta inatajable.
a) Encontrá el módulo de la velocidad inicial para que esto suceda (en función de α y h).
b) Suponiendo que B = 9,15 m, α = 20°, h = 1,85 m y que la pelota, después de pasar la barrera, pica sobre la
línea de gol, calculá la distancia entre la barrera y el arco.
Problema 16
Durante las erupciones volcánicas trozos de rocas pueden
ser proyectados por el volcán. ¿A qué velocidad inicial
tendría que ser eyectado de la boca del volcán uno de estos
trozos, formando un ángulo de 35º con la horizontal, para
que caiga en el punto A?
35°
3 km
A
9 km
Objetivo de los ejercicios siguientes: practicar las herramientas adquiridas con problemas tomados de distintos
libros de texto de Física.
Problema 17
Holton. Introducción a los conceptos y teorías de las ciencias físicas
Un muchacho arroja una piedra verticalmente y hacia abajo desde un piso a 50 m de altura, comunicándole
una velocidad inicial importante. Si la piedra llega al suelo en 1.8 s, ¿con qué velocidad inicial la arrojó? Hacer una
lista de las limitaciones, condiciones impuestas e idealizaciones más importantes para resolver el problema.
Problema 18
Sears-Zemansky-Young. Física universitaria
Un cuerpo se mueve en el eje x con aceleración constante a = 4ms -2. En el instante t = 0 se encuentra en x = 5 m y
su velocidad es v = 3 ms-1
a) Hállese la posición y la velocidad en el instante t = 2 s.
b) ¿Dónde se encuentra el cuerpo cuando su velocidad es de 5 ms -1?
Problema 19
Sears-Zemansky-Young. Física universitaria
El movimiento de una partícula según una línea recta se describe por la función:
x = (6 m) + (4 ms-2) t2 – (1 ms-4) t4
Supóngase que t es positiva.
a) Hállense la posición, la velocidad y la aceleración en el instante t = 2 s.
b) ¿Durante qué intervalo de tiempo la velocidad es positiva?
c) ¿Durante qué intervalo de tiempo x es positiva?
d) ¿Cuál es la velocidad positiva máxima alcanzada por la partícula?
Problema 20
Resnick-Halliday. Física.Parte I
Se deja caer un cuerpo a partir del reposo y cae libremente. Determínese la posición y velocidad del cuerpo
después de 1.0, 2.0, 3.0 y 4.0 segundos de caída.
Problema 21
Hetch. Física en perspectiva.
John Wayne, en una vieja película de vaqueros, va en lo alto de un tren que se desplaza por un tramo de vía recto a
48 km/h mientras lo persigue la habitual banda de malos. Lanza inteligentemente una bomba encendida hacia
arriba a una velocidad de 35 km/h. ¿Cúando y dónde caerá (despreciando el rozamiento del aire)? Dibújese un
esquema de la trayectoria.
Problema 22
Resnick-Halliday. Física.Parte I
A parachutist bails out and freely falls 50 m. Then the parachute opens, and thereafter she decelerates at 2.0 m/s 2.
She reaches the ground with a speed of 3.0 m/s.
a) How long is the parachutist in the air?
b) At what height does the fall begin?
Un paracaidista, después de saltar, cae 50 m sin rozamiento. Cuando se abre el paracaídas, retarda su caída 2.0
m/s2. Llega al suelo con una velocidad de 3.0 m/s.
a) ¿Cuánto tiempo dura el paracaidista en el aire?
b) ¿Desde qué altura saltó?
Problema 23
Tipler. Física.
Una partícula se mueve con una velocidad dada por v = 8.t – 7, estando v expresada en metros por segundo y t en
segundos.
a) Hallar la aceleración media en el intervalo de 1s que empieza en t = 3s y acaba en t = 4s
b) Hacer un gráfico de v en función de t.
c) ¿Cuál es la aceleración instantánea en un instante cualquiera?
Problema 24
Tipler. Física.
La distancia mínima en que se para un coche sin bloquearse las ruedas es de 50 m cuando marcha a 90 km/h.
Hallar la aceleración, admitiendo que es constante, y expresar la respuesta en fracción de la aceleración de la
gravedad. ¿Cuánto tiempo tarda en detenerse?
Problema 25
Alonso - Finn. Física.
Un emisor de electrones de un tubo de televisión produce electrones con una velocidad de unos 6x107 ms-1. La
distancia desde el emisor hasta la pantalla es de 0.40 m. Si los electrones son lanzados inicialmente de manera
horizontal, calculas la desviación vertical con respecto a una recta, debida a la acción de la gravedad.
Problema 26
Alonso - Finn. Física.
Se dispara un proyectil con una velocidad de 100 ms-1 y un ángulo de 60 grados con la horizontal. Calcule:
a) el alcance horizontal
b) la altura máxima
c) el tiempo de vuelo
d) la velocidad y la altura después de 10 s
e) exprese las coordenads y las componentes de la velocidad y aceleración
Problema 27
Serway. Física Tomo I.
En un bar local, un cliente hace deslizar un jarro vacío de cerveza para que vuelvan a llenarlo. El cantinero
está momentáneamente distraído y no ve el jarro, el cual cae de la barra y golpea el piso a 1.40 m de l base de la
misma. Si la altura de la barra es de 0.860 m
a) ¿con qué velocidad abandonó el jarro la barra?
b) ¿cuál fue la dirección de l velocidad del jarro justo antes de chocar con el piso?
Problema 28
Serway. Física Tomo I.
Un proyectil se dispara de tal manera que su alcance horizontal es igual a tres veces su máxima altura.
¿Cuál es el ángulo de disparo?
Problema 29
Serway. Física Tomo I.
Una pulga puede brincar una altura vertical h.
a) ¿cuál es la máxima distancia horizontal que puede saltar?
b) ¿cuál es el tiempo en el aire en ambos casos?