Unidad 5: Óptica geométrica

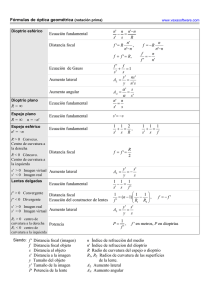
Unidad 5: Óptica geométrica
La óptica geométrica estudia los fenómenos luminosos utilizando el concepto de rayo, sin
necesidad de considerar el carácter electromagnético de la luz.
La óptica geométrica se basa en cuatro hechos fundamentales:
1.2.3.4.-
La luz se propaga en línea recta (denominada rayo) en medios isótropos.
Los rayos no interfieren entre sí en su propagación.
Se cumple las leyes de reflexión y refracción.
Los rayos de luz siguen trayectorias reversibles.
Imagen 1 wikipedia Creative Commons
Dioptrio
Un dioptrio es un sistema óptico formado por una superficie en la que se refracta la luz y
que separa dos medios transparentes, homogéneos e isótropos, de distinto índice de
refracción.
Elementos principales
Lo elementos principales de un dioptrio son:
-Centro de curvatura: Centro de la superficie esférica a la que pertenece el dioptrio esférico.
-Radio de curvatura: Radio de dicha superficie.
-Eje óptico: El eje de simetría de la superficie esférica.
-Centro óptico: Punto de corte del dioptrio y el eje óptico.
Un
dioptrio
separa
dos
y con
Enviar
medios,
,
índice de refracción.
e
Tipos y convenio de signos
Señala si las siguientes afirmaciones son verdaderas o falsas:
La distancia del objeto, situado delante del dioptrio es positiva.
Verdadero n
j Falso n
k
l
m
j
k
l
m
Si el dioptrio es cóncavo, el radio tiene signo negativo.
Verdadero n
j Falso n
k
l
m
j
k
l
m
Sólo existen dioptrios esféricos
Verdadero n
j Falso n
k
l
m
j
k
l
m
Dioptrio esférico
En el dioptrio esférico, la superficie que separa los dos medios es esférica.
Ecuación fundamental del dioptrio esférico
Esta ecuación permite calcular la distancia imagen s’ en función de la distancia objeto s, el radio
de curvatura, R, y los índices de refracción, n y n’, de ambos medios.
Un dioptrio convexo tiene un radio de 3 cm. Si los índices de refracción son 1,3 y 1,6 para
el primero y segundo medio. Índica a que distancia se forma la imagen de un objeto que
está colocado 15 cm delante de la superficie que separa ambos medios.
Es decir, como s’ es positivo, la imagen se forma detrás del dioptrio.
¿Es importante que el dioptrio sea cóncavo o convexo?
El estudio de los dioptrios esféricos es importante debido a que en los espejos y las lentes,
que son los componentes fundamentales de los instrumentos ópticos, la luz se comporta
siguiendo leyes similares a las del dioptrio esférico.
Un dioptrio cóncavo tiene un radio de 2 cm. Si los índices de refracción son 1,2 y 1,5 para
el primero y segundo medio. Índica a que distancia se forma la imagen de un objeto que
está colocado 10 cm delante de la superficie que separa ambos medios.
j -0,5 m
k
l
m
n
j +0,5 m
k
l
m
n
j -0,055 m
k
l
m
n
j +0,055 m
k
l
m
n
Parámetros de los dioptrios esféricos
Delante de un dioptrio cóncavo que separa dos medios, de índices de refracción 1,20 y
1,47, se coloca, a una distancia de 18 cm, una botella de 5 cm de altura. Calcula el
tamaño de la imagen que se forma si el radio del dioptrio es de 15 cm.
Como la y’ es positiva, la imagen que se forma está en el mismo sentido que el objeto y,
como la s’ es negativa, se encuentra delante de la superficie del dioptrio.
A una distancia de 10 cm delante de un dioptrio convexo, que separa dos medios de índices
de refracción n=1,2 y n'=1,4, se coloca un objeto de 8 cm de tamaño. Si la imagen aparece
a 5 cm detrás del dioptrio, ¿qué tamaño tiene ésta?
j -4 cm.
k
l
m
n
j +4 cm.
k
l
m
n
j -3 cm
k
l
m
n
j +3 cm
k
l
m
n
Dioptrio plano
El dioptrio plano es un caso particular del dioptrio esférico, donde
podemos tomar el radio de curvatura como infinito.
Un dioptrio plano se tiene, por ejemplo, cuando observamos un objeto sumergido
en agua desde fuera y tenemos una sensación distorsionada de la distancia real a
la que está el objeto de la superficie.
La relación entre la distancia real que ocupa el objeto y la aparente es:
que permite calcular la distancia que existe entre la superficie y la imagen en
función de la distancia del objeto a la superficie y de los índices de refracción de
ambos medios.
Un dioptrio plano...
c Es un caso particular de los dioptrios esféricos con radio de curvatura infinito
d
e
f
g
c No tiene nada que ver con los dioptrios esféricos
d
e
f
g
c Es un caso de dioptrio esférico con radio de curvatura igual a cero
d
e
f
g
Mostrar Información
En un dioptrio plano
c El objeto y la imagen están en diferentes medios.
d
e
f
g
c
d
e
f
g
El objeto y la imagen están en el mismo medio o en otro según los índices de
refracción.
c El objeto y la imagen están en el mismo medio.
d
e
f
g
Mostrar Información
Tamaño de la imagen
A partir de la ecuación del aumento lateral podemos deducir el tamaño de la
imagen:
Es decir, el tamaño de la imagen es igual al del objeto.
En el fondo de un cubo lleno de agua (n=1,33) se coloca un bolígrafo de 5 cm. La
distancia aparente del objeto a la superficie es de 25 cm. Calcula la profundidad de cubo
y el tamaño de la imagen del bolígrafo.
En el ejemplo anterior, ¿cuál sería la posición de la imagen del bolígrafo si éste tuviera una
longitud de 10 cm?
c -0,666 cm
d
e
f
g
c -0,333 cm
d
e
f
g
c +0,333 cm
d
e
f
g
c +0,666 cm
d
e
f
g
Mostrar Información
¿y su tamaño?
c 5 cm
d
e
f
g
c 10 cm
d
e
f
g
c 20 cm
d
e
f
g
c 1 cm
d
e
f
g
Mostrar Información
Cuando vemos algo debajo del agua, ¿su tamaño es engañoso?
Espejo plano
En el espejo tiene lugar la reflexión. La reflexión es un caso particular de la refracción.
El medio en el que se encuentra el rayo tras incidir es el mismo, por lo que el índice de
refracción, n, es el mismo, pero como la trayectoria del rayo cambia de sentido, se puede
escribir como si el índice fuera negativo → n’=-n.
La distancia focal se puede deducir a partir de la expresión del dioptrio plano:
El tamaño de la imagen, como ocurría en el caso del dioptrio plano, es igual que el del objeto.
Entonces, ¿qué ve un observador al mirar un espejo?
Un perchero de 1 m de altura se sitúa a 2 m de un espejo. ¿dónde se forma la imagen?
¿qué altura tiene la imagen del perchero?
La altura es de 1m y se sitúa a 2 metros detrás del espejo.
Rellena los espacios en blanco.
Los rayos, tras incidir en un
aunque, como cambian de
un medio con el
Enviar
, siguen estando en el mismo medio
al reflejarse, se comportan como si estuvieran en
índice de refracción pero con
sentido.
Espejo esférico
En los espejos esféricos tiene lugar la reflexión y su superficie es curva.
Los espejos esféricos son cóncavos cuando la superficie que refleja la luz es la interna (R<0) y
convexos si la superficie reflectante es la externa (R>0).
En este caso la ecuación general se puede obtener a partir de las del dioptrio esférico pero, al
igual que pasaba con el espejo plano → n’=-n.
La distancia focal, deduciendo a partir del dioptrio esférico, es:
que es la ecuación fundamental de los espejos esféricos. Con esta ecuación se puede deducir
que
por lo que sólo existe un punto focal y su distancia es igual a la mitad del radio de la curvatura.
Lee el siguiente texto sobre espejos esféricos y rellena los espacios en blanco.
Los espejos esféricos son un caso particular de los
curvatura pueden ser
esféricos. Según su
, si la cara que refleja la luz es la interna, o
, si es la cara externa.
En los espejos esféricos sólo existe
radio de curvatura.
Enviar
punto focal cuya distancia es la
del
Tamaño de la imagen
A partir de la ecuación general del dioptrio esférico se puede calcular el tamaño relativo del
objeto y la imagen teniendo en cuenta que:
Delante de un espejo cóncavo cuyo radio es de 50 cm se sitúa, a una distancia de 80 cm
de su punto medio, un bote de 10 cm de altura, perpendicularmente al eje óptico del
espejo. Calcula la distancia focal, la posición y el tamaño de la imagen.
El foco y la imagen están delante del espejo y la imagen se queda invertida, tal y como
indican los signos negativos.
En los espejos esféricos, el hecho de que sean cóncavos o convexos...
c ...no influye en los tamaños relativos.
d
e
f
g
c ... no influye en la posición de la imagen.
d
e
f
g
c ...hace que tengamos un foco o dos.
d
e
f
g
c ...cambia el signo del foco, y a partir de éso, influye en los demás parámetros.
d
e
f
g
Mostrar Información
Formación de imágenes
Para obtener la imagen de un objeto hay que trazar tres rayos:
-uno (morado) paralelo al eje óptico que se refleja pasando por el foco si es cóncavo o que
parece que proviene del foco si es convexo.
-otro (rojo) que pasa por el centro de curvatura si es cóncavo o se dirige a él si es convexo y
que tras incidir sigue con la misma trayectoria
-y un tercero (verde) que pasa por el foco del cóncavo, o se dirige a él tras incidir en el
convexo, y se refleja paralelo al eje óptico.
El punto de corte forma la imagen real.
Practica cómo varía la formación de imágenes en espejos esféricos:
http://www.educaplus.org/luz/espejo2.html
http://enebro.pntic.mec.es/~fmag0006/op_applet_26.html
Lentes delgadas
Una lente es un medio transparente limitado por dos superficies, de las cuales al menos una ha
de ser curva.
Tipos:
Convergentes: Más delgadas en los extremos que en el centro.
Divergentes: Más delgadas en el centro.
Se consideran lentes delgadas cuando el grosor de la lente es pequeño comparado con otras
magnitudes como pueden ser los radios.
Las lupas son ejemplos de lentes convergentes biconvexas.
Imagen 2 wikipedia Lic. Creat. Comm.
Las lentes son espacios
denominan
pequeño. Pueden ser
Enviar
limitados por
superficies. Se
cuando el grosor, comparado con otras magnitudes es
o
.
Ecuación fundamental
La ecuación fundamental de las lentes delgadas se puede deducir empleando las ecuaciones del
los dioptrios esféricos, teniendo en cuenta que una lente tiene dos superficies, con radios R1 y
R2 .
En los casos en los que una superficie es plana considera como si fuera esférica con R infinito.
La ecuación fundamental de las lentes delgadas se puede escribir como:
que, introduciendo las distancias focales nos permite expresarla como:
Los radios de curvatura de las caras de una lente bicóncava delgada son 5,6 y 3,9 cm,
respectivamente, y su índice de refracción es n=1,5. Si se sitúa un objeto de 9 cm
delante de la lente, a 10 cm de la misma, calcula el tamaño de la imagen que se forma.
j -2,35 cm
k
l
m
n
j -3,85 cm
k
l
m
n
j -3,15 cm
k
l
m
n
¿cuál es la distancia focal?
j -4,6 cm
k
l
m
n
j -4,1 cm
k
l
m
n
j -3,2 cm
k
l
m
n
Tamaño de la imagen y potencia de la lente
Tamaño de la imagen
A partir de la ecuación fundamental, se puede deducir cual es la relación que existe entre el
tamaño del objeto y de la imagen que genera:
Potencia de una lente
La potencia de una lente se define como la inversa de su distancia focal imagen f’:
Un objeto luminoso esta situado a 10 cm de una lente divergente de potencia -8
dioptrias. Si la altura del objeto es de 3,5 cm. Calcula la distancia focal de la lente y la
posición y el tamaño de la imagen.
El foco y la imagen están delante del espejo y la imagen se queda invertida, tal y como
indican los signos negativos.
Los radios de curvatura de las caras de una lente bicóncava delgada son 5,6 y 3,9 cm,
respectivamente, y su índice de refracción es n=1,5. Si se sitúa un objeto de 9 cm delante
de la lente, a 10 cm de la misma, calcula el tamaño de la imagen que se forma.
j 2,84 cm
k
l
m
n
j 1,46 cm
k
l
m
n
j 3,25 cm
k
l
m
n
¿y el foco de la lente?
j -0,36 dioptrias
k
l
m
n
j -0,30 dioptrias
k
l
m
n
j -0,22 dioptrias
k
l
m
n
¿Qué pasos he de seguir para encontrar la relación entre el tamaño del objeto y de la
imagen en los problemas de lentes según los datos que me den?
Formación de la imagen
Existen tres rayos cuyas trayectorias pueden ser trazadas de manera sencilla:
-Un rayo (morado) paralelo al eje óptico que, una vez refractado, pasa por el foco f’.
-Un rayo (rojo) que pasa por el centro de la lente y no se desvía.
-Un rayo (verde) que pasa por el foco f y se refracta en paralelo al eje óptico.
Selecciona la opción verdadera y deja la falsa sin marcar.
En las lentes bicóncavas, el foco imagen está delante de la lente.
Verdadero n
j Falso n
k
l
m
j
k
l
m
En las lentes biconvexas, el foco del objeto está detrás de la lente.
Verdadero n
j Falso n
k
l
m
j
k
l
m
Observa cómo varía la imagen según la distancia focal en lentes convergentes y
divergentes.
http://www.educaplus.org/luz/lente2.html
http://enebro.pntic.mec.es/~fmag0006/op_applet_20.htm
http://web.educastur.princast.es/proyectos/jimena/pj_franciscga/Eval8.swf
Sistemas ópticos
Los sistemas ópticos son sistemas que trabajan con dos o más lentes
Tipos
Las lentes pueden estar:
Acopladas: Es decir, en contacto una con la otra, en cuyo caso la potencia es la suma
algebraica de las potencias individuales.
Separadas: la imagen de una actúa como objeto de la otra, y así sucesivamente.
Ejemplos: cámara de fotos, microscopio, telescopio...
Cámara de fotos
Img. 3 wikipedia Licencia Creat. Com.
Telescopio
Img. 4 wikipedia Licencia Creat. Com.
Microscopio
Img. 5 wikipedia Licencia Creat. Com.