UNIDAD 5 LAS ONDAS
Anuncio

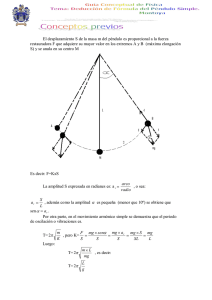
UNIDAD 5 LAS ONDAS. Oscilación. Una oscilación es un movimiento repetido de un lado a otro en torno a un punto fijo o de equilibrio. Ejemplos de objetos que oscilan son el péndulo, la cuerda de una guitarra y una esfera en el extremo de un resorte. Imaginemos una esfera atada en un extremo de un resorte. En el punto de equilibrio, no hay movimiento; pero si jalamos la esfera y la soltamos, esta volverá al punto de equilibrio, subirá y volverá a bajar periódicamente. Este es un movimiento oscilatorio. Desde luego que, una vez que se agote la energía del sistema, la esfera volverá al equilibrio. Este fenómeno también ocurre en la cuerda de una guitarra o en un péndulo. 2.1 Movimiento armónico simple (MAS) El movimiento armónico simple (MAS) es el más importante de los movimientos oscilatorios. Se llama armónico porque la ecuación que lo define es la función seno (o del coseno). Desplazamiento en el MAS. En el movimiento armónico simple, el desplazamiento del cuerpo, desde su posición de equilibrio, en función del tiempo viene dado por la siguiente ecuación: X = A Sen (ωt + β) En la ecuación anterior, se tiene que: A es la amplitud: el máximo desplazamiento desde la posición de equilibrio. ω es la frecuencia angular (en radianes). Esta se calcula así: ω = 2 π f = 2 π /T. f: frecuencias; T: período. β es la constante de fase. Frecuencia (f) y período (T). Recordemos que la frecuencia es el número de ciclos por segundo y el período es el tiempo que tarda el cuerpo por ciclo; es decir que T = 1/f. Por ejemplo, si la frecuencia es 2 ciclos/s; entonces el período es ½ s = 0.5 s. Constante de fase (β). Si un cuerpo inicia sus oscilaciones desde una posición distinta a la posición de equilibrio, se dice que existe un desfase en su movimiento. La medida de este desfase es lo que se conoce como constante de fase. En los ejercicios que resolveremos, iniciaremos el movimiento desde la posición de equilibrio; es decir que β = 0. Por lo tanto la posición será: X = ASen (ωt) La posición será positiva arriba y a la derecha, y será negativa abajo o a la izquierda. Velocidad y aceleración en el MAS. La velocidad y la aceleración en el MAS vienen dadas por las ecuaciones: v = ω A C o s (ωt) y a = - ω 2 X Equilibrio El movimiento en un resorte. En el diagrama se jala el resorte (por la esfera) y se suelta. En ese instante su velocidad es cero; luego su velocidad comienza a aumentar hasta un máximo en el punto de equilibrio y llega de nuevo a cero en el otro extremo (amplitud: máxima compresión del resorte). Luego comienza a moverse de nuevo, pero en sentido contrario, recorriendo las mismas velocidades (negativas). Si no hay pérdida de energía, la magnitud de su velocidad será la misma cada vez que pase por la línea punteada (ya sea que se acerque o se aleje del punto de equilibrio) Como vemos, existe una velocidad; pero esta velocidad cambia de magnitud en cada punto y también cambia de sentido; por lo tanto existe una aceleración. El movimiento de un péndulo ideal. Un péndulo ideal es aquel en el que no hay pérdida de energía. Esto se debe a que no hay fricción con el viento o en los puntos en movimiento. Por ejemplo, no hay fricción entre el hilo (cuerda) y el punto en donde está amarrado. Supongamos que el péndulo del diagrama es ideal; por lo tanto se moverá indefinidamente, de manera P que siempre pasará con la misma velocidad por un determinado punto. Si el péndulo se suelta en Q, se moverá circularmente, llegará a R, luego a S; aquí se detendrá y, en sentido contrario, pasará de nuevo θ por R y llegará a Q, donde se detendrá de nuevo. La máxima velocidad la alcanza en el punto de equilibrio, R (punto más bajo) Una oscilación completa se da cuando la esfera, partiendo de Q, vuelve a Q. El ángulo ℓ θ nos da la amplitud (QR) de la oscilación. En un péndulo ocurre que el tiempo para una oscilación NO depende Desplazamiento X de la masa que cuelga, sino únicamente de la longitud de la cuerda y de la gravedad. Matemáticamente, el período T es: S 0.5 T = 2π ℓ/g = 2π (ℓ/g) (no olvidemos que estamos tomando el M K valor de g igual a 10 m/s2) R Q Amplitud Podemos observar que el período NO depende del recorrido de la masa colgante. Esto significa que el período será el mismo tanto si el recorrido QS es de 5 cm o de 10 cm; o que recorra QS o MK. Esto parece ilógico, pero así es. En realidad lo que ocurre es que para oscilaciones MK la velocidad es menor, de manera que el período es el mismo que en una oscilación SQ. Por otra parte, π no son grados sino radianes; es decir: no son 180° sino 3.14 radianes (3.14 rad) Como en el resorte, en el péndulo tenemos una velocidad que cambia en cada punto, por lo que existe una aceleración. Ejemplo 16. Un péndulo de 2 metros de longitud tiene una amplitud de 1.5 m. Calcular: 1. el período 2. las posiciones en 1, 2 y 3 segundos 3. los tiempos en que la esfera alcanzará la máxima posición 4. los tiempos en que la esfera pasará por el punto de equilibrio 5. la magnitud de la máxima y la mínima velocidad alcanzada 6. la velocidad en los tiempos 0 s, 0.1 s, 0.2 s, 0.3 s, 0.4 s, 0.5 s, 0.6 s, 0.7 s, 0.8 s, 0.9 s, 1 s, 1.1 s, 1.2 s, 1.3 s y 1.4 s. Solución. 1. 0.5 0.5 Calculemos T: T = 2π(ℓ/g) = 6.28(2/10) = 2.81 T = 2.808 s. Es decir que la esfera tarda, desde su posición de equilibrio, 2.808 segundos para subir hacia la derecha (o izquierda), regresar a la posición de equilibrio, subir hacia la izquierda (o derecha) y regresar de nuevo a la posición de equilibrio. Aquí se muestran los 4 movimientos. 4 2. Las posiciones en 1, 2 y 3 segundos se calculan con 3 X = A Sen (ωt) Para 1 segundo: X = A Sen (ωt) = 1.5 Sen(ω(1)) Como ω = 2π/T = 6.28/(2.808) = 2.236 rad/s Tenemos que: X = A Sen (ωt) = 1.5 Sen(2.236(1)) = 1.18 X = 1.18 m. Para 2 y 3 segundos, obtenemos: X = A Sen (ωt) = 1.5 Sen(2.236(2)) = -1.457 X = -1.457 m. negativo porque está a la izquierda de la posición de equilibrio. X = A Sen (ωt) = 1.5 Sen(2.236(3)) = 0.618 X = 0.618 m. 3. Los tiempos en que la esfera alcanzará la máxima posición. Si nos basamos en el diagrama anterior, una oscilación se divide en 4 segmentos: subir (derecha)–bajar (derecha)–subir (izquierda)–bajar(izquierda) Por lo tanto en cada segmento tardará ¼ del período: 2.808/4 s = 0.702 s. Por lo tanto alcanzará la máxima posición (máxima altura) en los tiempos 0.702 s y 3(0.702) s; es decir, en 0.702 s y 2.116 s. Comprobémoslo. Para 0.702 s, la posición es: X = A Sen (ωt) = 1.5 Sen(2.236(0.702)) = 1.5 X = 1.5 m. Para 2.116 s, la posición es: X = A Sen (ωt) = 1.5 Sen(2.236(2.116)) = -1.5 X = -1.5 m el – indica que está en el otro extremo: a la izquierda. Desde liego que, como el péndulo sigue oscilando indefinidamente, habrá infinitos tiempos en los que llegará a la máxima altura. Estos tiempos son: n(0.702) + 2.808 s y n(2.116) + 2.808 s para todo n entero (y positivo). 4. los tiempos en que la esfera pasará por el punto de equilibrio. Evidentemente, al subir y bajar llega a su posición de equilibrio; es decir, a la mitad del tiempo de una oscilación: 2.808/2 s = 1.404 s. comprobémoslo: X = A Sen (ωt) = 1.5 Sen(2.236(1.404)) = 0 X = 0 m. 5. Las magnitudes de la máxima y la mínima velocidad alcanzadas. En un péndulo, en la altura máxima, la velocidad es la mínima, y es cero. Calculemos la máxima velocidad. Esta se da en el punto de equilibrio; y por el punto de equilibrio pasa en 1.404 segundos. Calculemos la velocidad: v = ω A Cos(ωt) = 2.236(1.5) Cos (2.236(1.404)) = -3.354 v = -3.354 m/s. el sino – indica que va hacia la izquierda. Como lo que nos interesa es la magnitud, tenemos que: v = 3.354 m/s. Si tomamos el tiempo de una oscilación (2.808), obtenemos: v = ω A Cos(ωt) = 2.236(1.5) Cos (2.236(2.808)) = 3.354 v = 3.354 m/s. ya va hacia la derecha. 6. La velocidad para cada tiempo se muestra en la tabla siguiente: las velocidades en los tiempos 0 s, 0.1 s, 0.2 s, 0.3 s, 0.4 s, 0.5 s, 0.6 s, 0.7 s, 0.8 s, 0.9 s, 1 s, 1.1 s, 1.2 s, 1.3 s y 1.4 s, t 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 v 3.354 3.27 3.02 2.63 2.1 1.46 0.762 0.018 -0.72 -1.43 -2.07 -2.6 -3 -3.26 -3.35 Actividad 27. Determinar el período de un péndulo si su longitud es de: a. 0.5 m ________ b. 1 m ________ c. 1.5 m ________ d. 2 m ________ e. 2.5 m ________ f. 3 m ________ g. 3.5 m ________ h. 4 m ________ i. 4.5 m ________ j. 5 m ________ (g = 10) Actividad 28. Determinar la longitud de un péndulo si su período es: a. 4.44 s ________ b. 4.21 s ________ c. 3.97 s ________ d. 3.71 s ________ e. 3.44 s ________ f. 3.14 s ________ g. 2.808 s ________ h. 2.43 s ________ i. 1.986 s ________ j. 1.404 s ____ Actividad 29. Determinar la frecuencia de un péndulo si su longitud es: a. 0.5 m ________ b. 1 m ________ c. 1.5 m ________ d. 2 m ________ e. 2.5 m ________ f. 3 m ________ g. 3.5 m ________ h. 4 m ________ i. 4.5 m ________ j. 5 m ________ Actividad 30. Para un péndulo de 3 metros de longitud y 2 metros de amplitud, determinar su posición en los tempos: a. 0.43 s _________ b. 0.86 s _________ c. 1.29 s _________ d. 1.72 s _________ e. 2.15 s _________ f. 2.58 s _________ g. 3.01 s _________ h. 3.44 s _________ 1 2 Actividad 31. Para un péndulo de 16.2278 metros de longitud y 10 metros de amplitud, determinar su posición en los tempos: a. 0 s _________ b. 1 s _________ c. 2 s _________ d. 3 s _________ e. 4 s _________ f. 5 s _________ g. 6 s _________ h. 7 s _________ i. 8 s _________ Actividad 32. Para un péndulo de 16.2278 metros de longitud y 20 metros de amplitud, determinar su posición en los tempos: a. 0 s _________ b. 1 s _________ c. 2 s _________ d. 3 s _________ e. 4 s _________ f. 5 s _________ g. 6 s _________ h. 7 s _________ i. 8 s _________ Actividad 33. Para un péndulo de 16.2278 metros de longitud y 20 metros de amplitud, determinar su velocidad en los tempos: a. 0 s _________ b. 1 s _________ c. 2 s _________ d. 3 s _________ e. 4 s _________ f. 5 s _________ g. 6 s _________ h. 7 s _________ i. 8 s _________ Discusión 17. Determinar la amplitud de un péndulo de 5 metros si se sabe que su posición es: a. 4.94 m en 1 s __________ b. 1.54 m en 2 s __________ c. -4.4584 m en 3 s __________ d. 1.2322 m en 2 s __________ e. 3.409 m en 1.5 s __________ f. 2.473 m en 1.75 s __________ g. 5.926 m en 1 s __________ h. 5.113 m en 1.5 s __________ i. 1.8484 m en 2 s __________ 2.2 Relación entre movimiento armónico y circular uniforme (MCU) Sin duda la relación entre el movimiento armónico y el circular uniforme es evidente. Un cuerpo posee movimiento circular uniforme si se mueve en círculo con velocidad lineal constante; es decir, si recorre la misma distancia en tiempos iguales. Por ejemplo, si un esfera se tarda siempre 3 segundos en dar una vuelta tiene MCU. La gran diferencia del MAS con el MCU es que en el MAS la velocidad del cuerpo cambia constantemente y también su aceleración. Sin embargo si nosotros observamos un cuerpo que se mueve con MCU colocando la mirada al nivel del plano en que está el cuerpo en movimiento, veremos que el cuerpo va y viene; es decir, tiene un movimiento oscilatorio. Esto puede captarse mejor observando la sombra proyectada por el cuerpo con MCU en un plano perpendicular al plano en el que se mueve. Este movimiento es senoidal (seno) La sombra se moverá desde una velocidad cero hasta una máxima, tal como ocurre en un péndulo. Por ejemplo, si en el diagrama la esfera se mueve recorriendo 45° cada minuto, se tiene que, partiendo de la posición indicada (P), la sombra recorrerá verticalmente Q una distancia mayor en el primer minuto que en el segundo minuto (a es mayor que b). Es decir que la velocidad de la sombra cambia constantemente. Se tiene que en el punto P la sombra alcanza su mayor velocidad hacia arriba; pero en Q su velocidad es cero. Ejemplo 17. Una esfera gira en un círculo recorriendo 5° cada segundo. Si el radio del círculo es 5 metros, calcular la distancia vertical recorrida P cada 5 grados durante los primeros 180°. El movimiento inicia en la posición P. S o l u c i ó n . De acuerdo con el diagrama, la distancia recorrida por la sombra es el lado opuesto del ángulo θ en el triángulo rectángulo formado. En dicho triángulo, la hipotenusa es el radio del círculo. Si aplicamos el seno, tenemos: Sen θ = opuesto / hipotenusa opuesto = hipotenusa (Senθ) Altura de 0° a 5°: opuesto = hipotenusa (Sen θ) = 5(sen 5°) = 0.43 m θ P Altura de 5° a 10°: opuesto = hipotenusa (Senθ) = 5(sen10°) = 0.86 m Tenemos que restarle 0.43 m 0.86 – 0.43 = 0.43 Distancia de 5° a 10° = 0.43 m Altura de 10° a 15°: opuesto = hipotenusa (Sen θ) = 5(sen15°) = 1.29 m Tenemos que restarle 0.87 m 1.29 - 0.87 = 0.42 Distancia de 10° a 15° = 0.42 m Altura de 15° a 20°: opuesto =hipotenusa (Senθ) = 5(sen20°) = 1.71 m Tenemos que restarle 1.29 m 1.71 - 1.29 = 0.42 Distancia de 15° a 20° = 0.42 m Altura de 20° a 25°: opuesto =hipotenusa (Senθ) = 5(sen25°) = 2 . 1 1 m Tenemos que restarle 1.71 m 2.11 - 1.71 = 0.4 Distancia de 20° a 25° = 0.4 m Altura de 25° a 30°: opuesto =hipotenusa (Senθ) = 5(sen30°) = 2 . 5 m Tenemos que restarle 2.11 m 2.5 - 2.11 = 0.39 Distancia de 25° a 30° = 0.39 m Altura de 30° a 35°: opuesto =hipotenusa (Senθ) = 5(sen35°) = 2 . 8 7 m Tenemos que restarle 2.5 m 2.87 - 2.5 = 0.39 Distancia de 25° a 30° = 0.37 m Siguiendo el mismo procedimiento, tenemos que: De 35° a 40° d = 3.21 – 2.87 = 0.34 De 40° a 45° d = 3.53 - 3.21 = 0.32 De 45° a 50° d = 3.83 – 3.53 = 0.3 De 50° a 55° d = 4.09 - 3.83 = 0.26 De 55° a 60° d = 4.33 – 4.09 = 0.24 De 60° a 65° d = 4.53 – 4.33 = 0.2 De 65° a 70° d = 4.7 – 4.53 = 0.17 De 70° a 75° d = 4.83 – 4.7 = 0.13 De 75° a 80° d = 4.92 - 4.83 = 0.09 De 80° a 85° d = 4.98 – 4.92 = 0.06 De 85° a 90° d = 5 - 4.98 = 0.02 De 90° a 95° d = 4.98 - 5 = - 0.02 De aquí en adelante, hasta 180°, se repetirán las distancias. De acuerdo con los resultados, se aprecia que la distancia recorrida por la sombra no es la misma en cada segundo. Esto indica que su velocidad cambia en cada instante. En el gráfico siguiente se muestran las b a distancias para una vuelta completa. Se aprecia que forman una función seno (o coseno) Actividad 34. Una esfera gira en un círculo recorriendo 10° cada segundo. Calcular la distancia vertical recorrida cada 10 grados durante los primeros 90°. El movimiento inicia en la posición P (como en los círculos anteriores) y el radio del círculo es 10 metros. Grados 0° a 10° 10° a 20° a 30° a 40° a 50° a 60° a 70° a 80° a 20° 30° 40° 50° 60° 70° 80° 90° Distancia Actividad 35. Una esfera gira en un círculo recorriendo 10° cada segundo. Calcular la distancia vertical recorrida cada 10 grados durante los primeros 90°. El movimiento inicia en la posición P (como en los círculos anteriores) y el radio del círculo es 20 metros. Grados 0° a 10° 10° a 20° a 30° a 40° a 50° a 60° a 70° a 80° a 20° 30° 40° 50° 60° 70° 80° 90° Distancia 2.3 Las ondas y su clasificación según la forma de propagación De todos es conocido que cuando se deja caer una piedra sobre el agua, se producen círculos concéntricos formados por olas a partir del punto en donde cayó la piedra (foco). Lo que ha ocurrido es que se ha perturbado el agua (puede ser cualquier sustancia) y esa perturbación se ha propagado. Lo que se propaga no son las moléculas de agua sino la energía de la perturbación. Una forma de propagación de esta energía es en forma de onda; es decir, por medio de un movimiento ondulatorio. Una onda es la propagación de una perturbación con movimiento armónico simple. Existen distintos tipos de ondas. Con las que más estamos en contacto es con las ondas sonoras, pero existen muchas ondas electromagnéticas, como las luminosas, y se cree que existen las ondas gravitacionales. Tipos de ondas según la forma de propagación. Las ondas son de 2 tipos: longitudinales o transversales. En las ondas compresión expansión longitudinales, el medio se desplaza en la dirección de la propagación. ejemplo, el aire (el medio) se comprime y 2.4 FenómenosPor ondulatorios La reflexión, la difracción y la superposición de ondas expande enlalarefracción, misma dirección en que avanza el sonido (esto se son fenómenos ondulatorios. Se estudiarán aquí y en la siguiente unidad. muestra en la figura). En las ondas transversales, el medio se Las ondas en el agua son transversales Reflexión. La reflexión es una propiedad del movimiento ondulatorio y NRayo reflejado desplaza en ángulo recto a la dirección de propagación. Por se produce cuando una onda choca contra una superficie. Al chocar, la Rayo incidente onda vuelvelas al medio que la reflexión ejemplo, ondasdeenpropagación; el agua deesundecir estanque avanzanpuede interpretarse como el rebote de la onda. Por ejemplo, si una onda sonora viaja por el aire y luego horizontalmente, pero el agua se desplaza verticalmente. choca contra un muro, retorna al aire. La reflexión puede ser total o parcial. Lo normal es que la energía de la onda sea reflejada parcialmente, mientras que otra parte de la β energía es absorbida por el medio de choque. Existe la reflexión regular. En esta reflexión la dirección de la onda reflejada está claramente determinada y cumple con dos condiciones: el rayo incidente y el rayo reflejado forman el mismo ángulo con la normal. Esto se muestra en el diagrama. Las superficies rugosas reflejan en muchas direcciones, y en este caso se habla de reflexión difusa. Difracción. La difracción es la desviación o expansión que sufre una onda después de pasar junto al borde de un objeto sólido o atravesar una rendija estrecha. La difracción se produce por superposición de ondas alternativamente, de manera que hay difracción constructiva (interferencia constructiva) y difracción destructiva (interferencia destructiva). Para el caso del sonido, si la difracción es constructiva, hay un aumento del sonido; si es destructiva hay una disminución (silenciadores). Gracias a la difracción podemos escuchar el sonido producido detrás de un muro, ya que las ondas rodean el muro. Lo mismo ocurre con la luz. Refracción. La refracción de una onda es el cambio de dirección que sufre al pasar de un medio a otro. Justamente esta es la causa por la cual observamos que una cuchara parece quebrarse al penetrar la superficie del agua. Esto se debe a que la luz a pasado de un medio (el aire) a otro medio (el agua). En la siguiente unidad estudiaremos lo que es el índice de refracción (iR) y lo calcularemos para un ángulo de incidencia de un rayo de luz. Interferencia. En la difracción se habló de la interferencia. Aquí seremos más explícitos. Hay interferencia cuando dos (o más) ondas se juntan para formar una nueva. ¿Qué pasa con la amplitud de la nueva onda? Supongamos que dos ondas con amplitudes A1 y A2 se juntan; entonces la nueva onda tendrá una amplitud que podrá ser, como mínimo, cero y como máximo A1 + A2. Cuando es cero, la interferencia es destructiva; cuando es máxima (A1 + A2), la interferencia es constructiva. Desde luego que obtener el máximo o el mínimo, pocas veces se logra. Esta es la razón por la cual los silenciadores no consiguen eliminar el ruido por completo. ¿De qué depende que se obtenga la mínima o la máxima o cualquier otra amplitud?... Esto depende de cómo se encuentren o junten las ondas. Por ejemplo, cuando las crestas (o los valles) de una onda se superponen o coinciden exactamente con las crestas (o los β β θ valles) de la otra onda, se dice que las ondas llegan en fase o están en fase: 0°. En estos casos, la amplitud de la onda resultante es la suma de las amplitudes de las individuales (A1 + A2) La mínima amplitud (cero) se produce cuando las ondas llegan en oposición de fase (desfase: 180°); es decir, cuando la cresta de una onda coincide exactamente con el valle de la otra onda, de manera que se cancelan mutuamente. R 1 Aquí 2 ondas en fase dan como resultado (R) una nueva con amplitud igual a la suma de las 2 amplitudes R R 2 Aquí 2 ondas en desfase dan como resultado (R) una nueva con amplitud cero 3 Aquí no hay fase ni desfase. La amplitud de R tendrá un valor entre cero y la máxima amplitud que se logró en el caso 1 2.5 Transmisión de energía y resonancia Energía. Una onda transmite energía sin mover materia. Por ejemplo, la luz transmite energía, pero no mueven materia. La energía está relacionada con la amplitud de la onda: a mayor amplitud, mayor energía. En el diagrama aparecen 2 ondas: la de mayor amplitud posee mayor energía. Recordemos que la amplitud es la máxima separación al punto de equilibrio. A A Resonancia. La resonancia está relacionada con la superposición de ondas y con la frecuencia. Hablaremos aquí de la resonancia mecánica. Cuando un sistema Mayor mecánico vibra en respuesta a una fuerza aplicada con la frecuencia natural del energía sistema o con una frecuencia próxima, se produce resonancia. Por ejemplo, si desviamos un péndulo de su posición de equilibrio y lo soltamos, vibrará con una frecuencia natural. Ocurre que si aplicamos continuamente una fuerza al péndulo con esa frecuencia natural (o una frecuencia próxima), la amplitud de la oscilación crecerá constantemente y puede destruir el sistema mecánico. Veamos lo anterior con un columpio. Si cada vez que un columpio llega a su máxima posición a la izquierda (como se muestra en el diagrama) le aplicamos una fuerza en la dirección del movimiento, la amplitud aumentará cada vez, de manera que el columpio rebasaría la altura del caño y podría ocurrir un accidente. Debido al peligro que representa la resonancia, los soldados frenan su marcha al pasar por un puente; pues puede ocurrir que la frecuencia de la marcha coincida con la frecuencia (o una de las frecuencias) del puente y se destruya. Ya se destruyó un puente por resonancia. Esto ocurrió en USA, y el puente era el Tacoma Narrows. Esto ocurrió en 1940. Su destrucción fue causada por un viento que vibró con la frecuencia natural del puente. Cuando no hay coincidencia con las frecuencias, los movimientos tienden a amortiguarse rápidamente. Para el caso del trampolín, si no hay resonancia, se detendrá más rápidamente que si lo dejáramos solo. Para impedir que una estructura resuene a una frecuencia determinada suele cambiarse su rigidez o su masa. El aumento de la rigidez aumenta la frecuencia natural, mientras que el aumento de la masa la disminuye. F velocidad 2.6 El sonido Puente Tacoma Narrows Hablaremos ahora del sonido. El sonido es un fenómeno físico que estimula el sentido del oído. Ya se dijo que es una onda longitudinal. Agregaremos ahora que toda onda longitudinal es mecánica. Una onda mecánica es aquella que necesita un medio físico para transportarse (aire, agua, una cuerda…). Para el caso, el sonido necesita de medios como los metales, los líquidos o el aire. Esto significa que no podríamos oír el sonido donde no hay aire; esto implica que no escucharíamos algún sonido en la Luna, pues ahí no hay aire ni otro tipo de atmósfera. Siempre que algo vibra produce sonido: las cuerdas de una guitarra, un cable, un pedazo de metal. Desde luego que para que llegue este sonido a nuestros oídos necesitamos del aire. Si vibrara una cuerda en la luna, no escucharíamos su sonido; pero si lo escucharíamos si colocáramos directamente el oído a la cuerda vibrante. Nuestras cuerdas vocales vibran cuando hablamos. Características del sonido. Son características del sonido (además de la reflexión, refracción e interferencia) la velocidad, la frecuencia, la amplitud, la intensidad y el timbre. Velocidad del sonido. El sonido puede viajar en cualquier medio y su velocidad dependerá del medio, además de la temperatura del medio. Por ejemplo, la velocidad del sonido en el aire es de 331.6 m/s a 0°C; pero a 20°C su velocidad es de 344 m/s. En cambio en el agua es de 1390 m/s a 0°C, y de 1484 m/s a 20°C. Otras velocidades son: hidrógeno a 0°C: 1280 m/s; cobre a 0°C: 3580 m/s; acero a 20°C: 5050 m/s; vidrio a 20°C: 5200 m/s. Se aprecia que en los líquidos la velocidad es mayor que en los gases; y en los sólidos es mayor que en los líquidos. Otro factor que afecta la velocidad del sonido es la densidad. La velocidad del sonido varía de forma inversamente proporcional a la raíz cuadrada de la densidad. Frecuencia del sonido. Dado que el sonido es una onda posee frecuencia. Cada sonido posee su propia frecuencia. La frecuencia la percibimos como tonos graves o agudos. Los sonidos que el oído humano es capaz de escuchar están comprendidos en el rango de 20 hercios a 20 000 hercios. Los sonidos arriba de 20000 Hz se conocen como ultrasonidos. La ciencia que estudia los ultrasonidos se llama ultrasónica. Una aplicación de la ultrasónica es el sonar. Este aparato se utiliza en la navegación y se basa en la reflexión de las ondas. El sonar emite pulsos de ultrasonido mediante un dispositivo transmisor sumergido; a través de un micrófono sensible, o hidrófono, capta los pulsos reflejados por posibles obstáculos o submarinos. Los submarinos modernos dependen del sonar para la detección de barcos enemigos. Como vemos, un sonar funciona como un radar. Amplitud del sonido. La amplitud de una onda de sonido es el grado de movimiento de las moléculas de aire en la onda. Cuanto mayor es la amplitud de la onda, más intensamente golpean las moléculas el tímpano y más fuerte es el sonido percibido. Intensidad del sonido. La intensidad de un sonido es la que nos permite escucharlo a cierta distancia. En este instante se ha producido un sonido de gran intensidad en algún lugar, pero no lo escuchamos porque ha ocurrido muy lejos. La intensidad se relaciona con la amplitud: a mayor amplitud, mayor intensidad. Timbre del sonido. El timbre es la característica del sonido que nos permite distinguir los tonos producidos por instrumentos distintos aunque las ondas sonoras tengan la misma amplitud y frecuencia. Por ejemplo pueden sonar con las mismas frecuencia, intensidad y amplitud un violín, un piano y un diapasón, pero el timbre será distinto: distinguiremos un instrumento de otro. De las tres fuentes, el diapasón es el que produce el tono más sencillo, que en este caso está formado casi exclusivamente por vibraciones con frecuencias de 440 Hz.