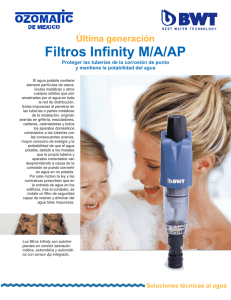
INVESTIGACIÌN OPERATIVA

INVESTIGACIÓN OPERATIVA
Guía de Trabajos Prácticos
Curso cuatrimestral para Ingeniería Industrial
1 de 1
CONTENIDO
PAGINA
1)
2)
3)
4)
5)
Programación Lineal Gráfica
Modelización y Resolución Gráfica
Modelización
Método Simplex y Casos Particulares
Programación Dual-Introducción al análisis
Post-Optimal
6) Programación Lineal - Análisis Post-Optimal
7) Modelos de Inventario
8) Programación por Camino Crítico
9) Teoría de Colas
10)Simulación
3
6
9
16
18
19
28
34
37
40
ANEXOS
Solución a los problemas de Programación Lineal
de los Capítulos 1 y 4
Solución a los problemas de Programación Lineal
del Capítulo 6
Tablas
2 de 2
46
59
68
1)
PROGRAMACIÓN LINEAL GRÁFICA
Resuelva los siguientes problemas para X1 y X2 no negativas.
1.1)
X1
X2
6 X1 + 4 X2
Z = 8 X1 + 3 X2
1.2)
-2 X1 +
X1 X1 +
X2
X2
X2
Z = 5 X1 + 2 X2
1.3)
X2
4 X1 + 6 X2
4 X1 - 3 X2
Z = 5 X1 + 2 X2
1.4)
6 X1 + 5 X2
X2
-2 X1 + 2 X2
Z = 5 X1 + 8 X2
3 de 3
≤ 3
≤ 6
≤ 36
MAX
≤
≤
≤
2
2
5
MAX
≤ 3
≤ 24
≤ 12
MAX
≤ 30
≥ 1
≤ 6
MAX
1.5)
X1 +
X2 ≤ 300
2,5 X1 + 4 X2 ≤ 1000
X2 = 200
X1
≤ 200
Z = 6 X1 + 2 X2
1.6)
X2
4 X1 + 6 X2
2 X1 + 2 X2
Z = -2 X1 + 4 X2
1.7)
X1
X1 +
X2
X1 + 2 X2
Z = 4 X1 + 4 X2
1.8)
2 X1 + 4 X2
4 X1 + 2 X2
3 X1
Z = 6 X1 + 4 X2
1.9)
-5 X1 + 3 X2
X1 +
X2
2 X1 +
X2
Z = 2 X1 + X2
4 de 4
MAX
≤
≤
≥
3
24
0
MAX
≤ 6
≤ 8
≤ 12
MAX
≤ 48
≤ 60
≤ 45
MAX
≥ 5
≤ 4
≥ 10
MAX
1.10)
X2
4 X1 + 6 X2
10 X1 - 30 X2
Z =
X1 +
8 X2
1.11)
X1
2 X1 +
X1 +
Z =
X1 -
X2
2 X2
X2
1.13)
Z =
MAX
≥ 2
≤ 10
≤ 8
≥ 1
2 X2
1.12)
Z =
≥ 2
≥ 24
≥ 30
X1 +
2 X1 + 3
- X1 + 2
X2
X2
X2
3 X1 +
X2
2 X1 +
X1 +
X1
X2
X2
3 X1 +
X2
5 de 5
MIN
≤
≤
≥
6
1
8
MAX
≤
≤
≤
8
6
4
MAX
2)
MODELIZACIÓN Y RESOLUCIÓN GRÁFICA
2.1) Es necesario alimentar racionalmente un rebaño de cabezas de
ganado.
Los
alimentos
deben
contener
necesariamente
cuatro
componentes
nutritivos : A,B,C,D.
Se encuentran disponibles en el mercado dos alimentos M y N cuyas
propiedades son: Un kilogramo de alimento M contiene 100gr. de A,
100gr. de C y 200gr. de D.
Un kilogramo de alimento N contiene 100gr. de B, 200gr. de C y 100gr.
de D.
Cada animal debe consumir como mínimo, por día 400gr. de A, 600gr. de
B, 2000gr. de C y 1700gr. de D.
El alimento M cuesta 10$/kg. y el N 4$/kg.
¿Qué cantidades de alimento M y N debe suministrarse a cada animal
diariamente para que la ración sea la más económica?
2.2) Una pequeña empresa de productos químicos debe consumir más de 40
m3/mes de un determinado alcohol debido a que ha firmado un contrato
con la municipalidad de la zona (este alcohol es producido en la misma
zona) y en compensación recibe beneficios impositivos.
Produce dos tipos de fertilizantes A y B. La tabla siguiente resume la
información básica:
PRODUCTO A
PRODUCTO B
CONSUMO DE ALCOHOL
3 m3/unidad
2/3
CONSUMO CICLOHEXANO
1 ton/unidad
2
Disponibilidad de Ciclohexano 20 ton/mes
m3/unidad
ton/unidad
Con estas restricciones y sabiendo que la contribución marginal es de
1200 $/unidad para el producto A y 400 $/unidad para el producto B
calcular el plan óptimo de producción.
2.3) Hay dos máquinas disponibles para la producción de dos productos.
Cada uno de los productos requiere los tiempos de proceso que se
indican en la tabla siguiente (expresados en horas/unidad).
PRODUCTO
1
2
DISPONIBILIDAD
MAQUINA
A
2
4
80 hs.
MAQUINA
B
3
2
60 hs.
El esquema del proceso productivo es el siguiente: Ambos productos
deben pasar sucesivamente por las dos máquinas A y B en ese orden, para
quedar totalmente terminados. Una máquina puede procesar un solo
producto por vez. El precio de venta del producto 1 es 60$/unidad y el
del producto 2 es de 50$/unidad. Se planea la operación para el mes
próximo. Cuál es el uso óptimo de estos recursos frente al objetivo de
maximizar las ventas? ¿Es conveniente conseguir 20 horas adicionales de
equipo B?
6 de 6
2.4) Se desea definir las cantidades a fabricar de dos productos:A y B
cuyo procesamiento se realiza en dos centros de máquinas, se conocen
los datos referentes a los tiempos de proceso y disponibilidades en los
centros. Se sabe además que debe cumplirse con un pedido mínimo de 50
unidades de A, y al mismo tiempo la producción de B debe ser por lo
menos cuatro veces superior a la producción de A.
Se conocen los márgenes brutos de beneficio de cada producto, y se
desea optimizar el beneficio total.
Tiempos unitarios
Producto
A
B
MAQUINA I
MAQUINA II
1
0,5
Margen bruto unitario
12
0,4
1
Disponibilidad
200
200
8
2.5)Dado el siguiente sistema de inecuaciones:
4 X1 - 2 X2 ≤ 4
4 X1 + 2 X2 ≤ 8
X1 +
X2 ≥ 1
y el funcional:
Z = 8 X1 + 4 X2
a) Encuentre un enunciado compatible con el mismo.
b) Resuélvalo gráficamente
c) Indique la o las soluciones al problema que hagan óptimo al
funcional.
d) Dé el valor de las variable débiles, sus unidades y
significado en cada uno de los vértices del poliedro.
2.6) Una empresa automotriz está equipada para producir automotores y
camiones. Su planta fabril está organizada en cuatro departamentos:
Estampado, montaje de motores, línea de montaje de automotores, y línea
de montaje de camiones.
La capacidad de cada departamento está limitada de la siguiente forma:
Estampado puede producir 25.000 autos o 35.000 camiones por año (o
cualquier combinación lineal convexa intermedia).
Montaje de motores 33.333 autos o 16.667 camiones por año (o cualquier
combinación lineal convexa intermedia).
Línea de montaje de autos 22.500 unidades por año
línea de montaje de camiones 15.000 unidades por año.
Se desea producir como mínimo 12.000 autos y 8.000 camiones por año,
estimándose asimismo en 18.000 unidades la cantidad demandada máxima de
automotores. El margen de beneficios es de 150.000 $/auto y de 125.000
$/camión.
Se desea conocer el plan de producción que haga máximo el margen total
de beneficios.
7 de 7
2.7) Dos aditivos "1" y "2" deben ser empleados para mejorar la calidad
de una nafta. Se deben cumplir las siguientes condiciones:
a) Como los aditivos no producen combustión es conveniente para evitar
la formación de depósitos en el carburador, que por cada 10 litros de
gasolina no se agregue más de 1/2 litro de aditivos.
b) La cantidad de aditivo "2" más dos veces la cantidad de aditivo "1"
debe ser como mínimo 1/2 litro por cada 10 litros de gasolina. De ésta
forma se logra una nafta de color óptimo.
c) Un litro de aditivo "1" por cada 10 litros de nafta significa que a
la nafta se le agregan 10 unidades de octanaje y un litro de aditivo
"2" por cada 10 litros de nafta, 20 unidades de octanaje.
La nafta sin aditivos posee un octanaje de 84 y se requiere que como
mínimo posea un número de octano superior a 90.
El costo del aditivo "1" es de 153 $/litro y el del aditivo "2" es de
400 $/litro.
8 de 8
3)
MODELIZACIÓN
3.1) Un taller de tejido de pullovers elabora varios modelos que se
pueden agrupar desde un punto de vista técnico-económico en tres tipos
diferentes de prendas: A, B, y C.
El taller posee dos máquinas (I y II), los pullovers A sólo pueden
hacerse en la máquina I, los C en la II y los B en la I o en la II.
Las dos máquinas trabajan dos turnos de 8 horas de lunes a viernes.
La materia prima utilizada es lana de dos calidades distintas M y N.
La M se usa en los pullovers tipo A y C. La N se usa en los pullovers
tipo B. De la lana tipo M es posible conseguir hasta 20 kilos por
semana y de la N hasta 36 kilos por semana.
Existe un compromiso con un importante distribuidor de entregar 10
pullovers de tipo B por semana.
No es necesario que las prendas que comienzan a fabricarse en una
semana se terminen durante la misma, es decir que pueden quedar
pullovers a medio hacer de una semana a la siguiente.
Los standard de producción, consumo de materia prima y beneficio
unitario para cada tipo de pullover se dan en el siguiente cuadro:
Standard de Producción
Standard de Materia Prima
hs/pullover
Kgs/pullover
I
A
B
C
Beneficio
Unitario
$/pullover
II
5
6
-
M
-
N
1,6
1,2
4
4
1,8
-
1000
1500
1800
3.2) Una fábrica de automotores cuenta con un taller propio para la
producción de los tableros de los vehículos de la fábrica, tarea que
también puede encomendarse a proveedores.
El proceso de fabricación de tableros es el siguiente (para cualquier
tipo de tablero):
COMPRA
ESTAMPADO
ARMADO
CABLEADO
AJUSTE
RECHAZO COMPRA
CONTROL
CALIDAD
RECHAZO PRODUCCIÓN
9 de 9
Aprobado
Los tableros comprados pasan también por el mismo sector de control de
calidad. La fábrica necesita cuatro tipos de tableros A, B, C y D para
los que se cuenta con los datos referentes a sus tiempos de proceso en
horas/tablero tal como se muestra en la tabla siguiente:
TABLERO
ESTAMPADO
ARMADO
CABLEADO
AJUSTE
A
B
C
D
0,05
0,05
0,05
0,05
0,10
0,12
0,14
0,18
0,20
0,25
0,30
0,25
0,08
0,10
0,06
0,10
DISPO.
1200
3600
5000
3000
CONTROL DE CALIDAD
PRODUCCIÓN COMPRA
0,02
0,03
0,03
0,03
0,03
0,05
0,04
0,04
3000
En la tabla se ha agregado la disponibilidad en horas de los sectores,
y el tiempo de control de calidad de los tableros comprados.
La fabrica necesita exactamente 4000 tableros A, 3000 tableros B, 8000
tableros c y 5000 tableros D.
Los costos de producción y compra son los siguientes, medidos en $:
Producción
Compra
A
5000
3000
B
6000
7500
C
12000
18000
D
10000
8000
Un registro estadístico de Control de Calidad indica que el 90% de los
tableros producidos por la fábrica son aprobados, y el resto debe
repetir la operación de ajuste. Con respecto a los tableros comprados,
es aprobado el 80% y el resto es devuelto al proveedor, siendo
controlado nuevamente al ser reintegrado por el proveedor. Para un
tablero reajustado el porcentaje es el mismo indicado.
Se desea definir las cantidades a producir y comprar de cada tablero,
para hacer mínimo el costo total de la operación.
3.3) Se fabrican dos productos A y B que requieren dos operaciones de
maquinado para estar en condiciones de ser vendidos. Estas operaciones
se realizan en tres equipos diferentes según se indica en la tabla
adjunta. La operación II puede realizarse en horas normales de equipo
2, en horas extras del mismo equipo o en cambio en el equipo 3.
En la tabla también se indican las disponibilidades de cada uno de los
equipos expresadas en horas, y la utilidad de cada producto según el
método de producción seguido expresado en $ cada 1000 piezas.
Se desea establecer el programa de producción que maximice la utilidad
de la fábrica. Se aclara que el programa de producción debe establecer
la cantidad de producto a fabricar por cada uno de los métodos
posibles.
10 de 10
Operación
Tiempos de
Producción (hs/1000 piezas)
Equipos
Producto A
I
II
1
2
2 extra
3
Utilidad ($/1000 piezas)
2
3
-
2
3
-
Tiempo
Disponible
Producto B
2
4
5
8
-
850 600 700
5
8
-
1600
5
10
1.000
600
200
800
1400 1300
3.4) Un fraccionador de Whisky importa el licor en tres distintas
graduaciones: A, B y C. Mediante la mezcla de estos de acuerdo a sus
fórmulas obtiene los Whiskies de calidades comerciales Escocés, Kilt y
Tartan.
Las citadas fórmulas especifican las siguientes relaciones entre los
elementos a mezclar:
MARCA
ESPECIFICACIÓN
PRECIO DE VENTA
$/litro
Escocés
No menos de 60% de A
No más de 20% de C
680
Kilt
No menos de 15% de A
No más de 60% de C
570
Tartan
No más de 50% de C
450
Se conocen asimismo las disponibilidades y precios de los licores A, B,
C que se indican en el siguiente cuadro:
TIPO
DISPONIBILIDAD (LITROS)
A
B
C
Se desea definir
beneficio total.
PRECIO DE COSTO ($/LITRO)
2.000
2.500
1.200
la
700
500
400
composición
de
cada
marca
para
maximizar
el
3.5) Plantear el modelo del problema que se enuncia a continuación,
indicando detalladamente:
A)Hipótesis y supuestos
B)Objetivos del problema
C)Variables reales, significado y unidades
D)Inecuaciones que constituyen el modelo, aclarando en cada caso
a qué restricción corresponde
E)Funcional
F)Variables slack, significado y unidades
11 de 11
Una fábrica elabora dos productos químicos P1 y P2 a partir de cuatro
materias primas (MP1, MP2, MP3, MP4) siguiendo el proceso que se
describe a continuación.
X1
X1
MP1
X4
X4
1
4
X3
X11
3
6
P1
5
X2
X13
MP2
X5
2
X14
X15
X9
X7
MP3
MP4
X17
X16
7
X10
X18
8
X12
P2
En el centro 3 se mezclan los resultados de los centros 1 y 2 en la
proporción 70/30. A la salida del centro 3, el resultado se separa en
la relación 40/60 para ir a los centros 4 y 5 respectivamente. En el
centro 5 se mezclan el resultado del centro 3, el resultado del centro
7 y la materia prima 4 en la proporción 60/20/20.
En el centro 7 se mezclan X14 y MP3 en la proporción 90/10
En el centro 8 la mezcla se produce en partes iguales.
En el centro 7 se produce una merma del 5% de todo lo que ingresa.
Al inicio del período de planeamiento se tiene la posibilidad de vender
la materia prima que no se empleará a los siguientes precios:
MP1: 8$/kg.
MP2: 7$/kg. MP3: 2$/kg. MP4: 15$/kg.
El costo de almacenamiento por kilogramo de materia prima y por mes es:
MP1: 3$/kg.mes MP2: 8$/kg.mes MP3: 10$/kg.mes MP4: 6$/kg.mes
Se asume que la materia prima consumida está 1/2 mes en promedio en
almacenes.
El costo de la materia prima y la disponibilidad es:
COSTO
MP1
MP2
MP3
MP4
4
5
1
6
$/kg
$/kg
$/kg
$/kg
DISPONIBILIDAD
INICIAL
2000
3000
1700
2500
kg/mes
kg/mes
kg/mes
kg/mes
Los centros procesan a la velocidad de entrada que se indica a
continuación. Además se dispone de dicho recurso en la medida
siguiente:
12 de 12
CENTRO
VELOCIDAD DE PROCESO
Kg/hora
1
2
3
4
5
6
7
8
10
15
20
12
18
20
10
15
DISPONIBILIDAD
horas/mes
300
150
180
250
240
120
100
280
El producto 1 se vende a 10$/Kg y el producto 2 a 15$/Kg.
Existen contratos que exigen que se fabrique al menos 30 Kg de producto
1 y 40 Kg de producto 2. Adicionalmente la cantidad de producto 1 debe
ser a lo sumo igual a la mitad de la cantidad del producto 2.
3.6) Dos aleaciones "A" y "B" se forman a partir de cuatro metales: I,
II, III, y IV según las siguientes especificaciones:
ALEACIÓN
"A"
ESPECIFICACIÓN
Como máximo 50% de I
Como máximo 30% de II
Como mínimo 50% de IV
"B"
Entre 40% y 60% de II
Como mínimo 30% de III
Como máximo 30% de IV
Los cuatro metales están contenidos en
diferentes minerales cuyos
porcentajes de composición, disponibilidad y costo están dados en la
siguiente tabla:
MINERAL
1
2
3
DISPONIBILIDAD
1000
2000
3000
I
II
20
10
5
10
20
5
% DE METAL
III
IV OTROS
30
30
70
30
30
20
10
10
0
COSTO
30
40
50
Los precios de venta de las aleaciones "A" y "B" son respectivamente
200 y 300 $/ton.
13 de 13
3.7) Una empresa fabrica y vende dos productos "A" y "B" cuyo diagrama
de proceso es el siguiente:
PRODUCTO A
método 1
2
1
4
PRODUCTO B
3
PRODUCTO A
método 2
El producto "A" puede seguir cualquiera de los dos procesos
alternativos de producción, mientras que para el producto "B" existe un
único procedimiento de fabricación.
Características y rendimiento de los productos según sus procesos:
PRODUCTO
A
B
CENTROS
ENTRADA(l/h)
RENDIMIENTO(%)
COSTO ($/h)
1
2(primera
vez)
4
2(segunda
vez)
3
300
450
90%
95%
1500
2000
250
400
85%
80%
1800
2200
350
75%
2500
1
3
4
500
480
400
90%
85%
80%
3000
2500
2400
Otros insumos:
El
centro
1
consume
10
litros
de
combustible
por
hora
de
funcionamiento, y los centros 2, 3 y 4 consumen respectivamente 20, 5 y
5 litros de combustible por hora.
Asimismo el centro 1 debe ser atendido por un operario, el centro 2 por
dos operarios simultáneamente y los centros 3 y 4 por un operario cada
uno mientras están en operación.
Se dispone de 800 litros de combustible diario y 48 horas hombre
diarias.
Costos, precios de venta y demanda máxima de cada producto:
PRODUCTO
COSTO MATERIA PRIMA
$/LITRO
A
B
50
60
PRECIO DE VENTA
$/LITRO
60
180
14 de 14
DEMANDA MÁXIMA
LITRO/DÍA
1750
1500
Disponibilidad de equipos: Al realizarse el estudio se verificó que los
centros 1 y 4 pueden funcionar como máximo 16 horas netas por día y los
centros 2 y 3 solamente 12 horas netas por día.
Distribución:
Los medios de despacho de la empresa están limitados a una capacidad
conjunta para "A" y "B" de 2500 litros diarios. Se pide determinar la
mezcla de ventas que maximize el margen de beneficios.
Se sugiere plantear el problema adoptando como incógnitas las
cantidades de cada producto obtenido al final del proceso (ejemplo: Xk
litros de producto "B").
Se puede repetir el planteo adoptando como incógnitas las cantidades de
materia prima que ingresan para producir cada producto (ejemplo: Xf
litros de materia prima B).
3.8) Una papelera debe cortar 1.000 rollos de papel de 1m de ancho en
rollos de 50cm, 30cm, y 20cm.
Para ello dispone de una máquina de corte que puede trabajar bajo 4
modos diferentes de operación. La tabla que sigue muestra la cantidad y
tipo de rollos que puede obtener en cada uno de los modos de trabajo:
Modo
50cm
I
II
III
IV
2
0
1
1
30cm
20cm.
0
3
1
0
0
0
1
2
Se deben obtener al menos 950 rollos de 50cm, 1000 rollos de 30cm y 960
rollos de 20cm. Cada rollo de 50cm se vende en $2, cada rollo de 30cm
en $1,5 y cada rollo de 20cm en $1. Cada rollo de 1m cuesta $1,5.
Plantear un modelo que permita hallar la programación óptima de la
máquina de corte.
3.9)Un hotel planea recibir a los participantes de una convención que
dura una semana. Para los banquetes previstos, la empresa organizadora
de la convención solicitó que se utilizaran manteles de un color
especial. El costo de dichos manteles es de 250 $/mantel. El lavado de
dichos manteles toma normalmente 2 días; es decir un mantel sucio,
enviado a lavar inmediatamente después de ser utilizado el día 2, es
regresado a tiempo para ser utilizado el día 5.
Sin embargo, la lavandería tiene también un servicio de mayor costo que
regresa los manteles en 1 día. Los gastos de lavandería son de 100
$/mantel y de 150 $/mantel respectivamente.
Debe considerarse además, que el hotel no desea (por las características de estos manteles), comprar más manteles que los necesarios
para el día, ni enviar manteles a lavar si no van a ser utilizados
durante esta convención. Plantear un modelo que permita calcular como
el hotel satisface sus necesidades minimizando gastos.
Día (i)
Manteles necesarios
1
5
2
6
3
7
15 de 15
4
8
5
7
6
9
7
10
4) MÉTODO SIMPLEX Y CASOS PARTICULARES
Resolver por el método simplex y gráficamente los siguientes
ejercicios. (En todos los casos los valores óptimos de las variables
deben ser no negativos).
4.1)
X1
Z =
6 X1
X2
+ 4 X2
8 X1
+ 3 X2
4.2)
-2 X1
X1
X1
Z =
+
+
X2
X2
X2
5 X1
+ 2 X2
4 X1
4 X1
X2
+ 6 X2
- 3 X2
5 X1
+ 2 X2
4.3)
Z =
4.4)
6 X1 + 5 X2
X2
-2 X1 + 2 X2
Z =
≤ 3
≤ 6
≤ 36
MAX
≤
≤
≤
2
2
5
MAX
≤ 3
≤ 24
≤ 12
MAX
≤ 30
≥ 1
≤ 6
5 X1 + 8 X2
MAX
Resolver por el método simplex y gráficamente los siguientes
ejercicios, explicando el tipo de solución obtenida y cómo se detecta
en la tabla final.
4.5)
X1 +
X2
2,5 X1 + 4 X2
X2
X1
Z =
6 X1 + 2 X2
4.6)
X2
4 X1 + 6 X2
2 X1 + 2 X2
Z =
≤ 300
≤ 1000
= 200
≤ 200
-2 X1 + 4 X2
16 de 16
MAX
≤
≤
≥
3
24
0
MAX
4.7)
X1
X1 +
X2
X1 + 2 X2
Z =
4 X1 + 4 X2
4.8)
2 X1 + 4 X2
4 X1 + 2 X2
3 X1
Z =
-5 X1 + 3 X2
X1 +
X2
2 X1 +
X2
2 X1 +
X2
4 X1 + 6 X2
10 X1 - 30 X2
X1 +
X1
2 X1 +
X1 +
X1 -
X2
2 X2
X2
4.13)
Z =
≥ 5
≤ 4
≥ 10
MAX
≥ 2
≥ 24
≥ 30
MAX
≥ 2
≤ 10
≤ 8
≥ 1
2 X2
4.12)
Z =
MAX
8 X2
4.11)
Z =
≤ 48
≤ 60
≤ 45
X2
4.10)
Z =
MAX
6 X1 + 4 X2
4.9)
Z =
≤ 6
≤ 8
≤ 12
X1 +
2 X1 + 3
- X1 + 2
X2
X2
X2
3 X1 +
X2
2 X1 +
X1 +
X1
X2
X2
3 X1 +
X2
17 de 17
MIN
≤
≤
≥
6
1
8
MAX
≤
≤
≤
8
6
4
MAX
5) PROBLEMA DUAL - INTRODUCCIÓN AL ANÁLISIS POST OPTIMAL
5.1) Plantear y resolver el problema dual correspondiente al ejercicio
4.2 y 4.8
5.2) Plantear y resolver el problema dual correspondiente al ejercicio
4.9 y 4.13
5.3) Obtener la tabla óptima dual del problema 4.2 a
tabla óptima del problema directo.
5.4) Obtener la tabla óptima dual del problema 4.7
tabla óptima del problema directo.
partir de la
a partir de la
5.5) Obtener la tabla óptima dual del problema 4.11 a partir de la
tabla óptima del problema directo
5.6) Obtener la tabla óptima del problema 4.1 si se incorpora al mismo
una nueva variable X3 con coeficientes 2, 1, 6 y C3=13
5.7)Obtener la tabla óptima del problema 4.4
siguiente restricción adicional: 4 X1 + 2 X2 ≤ 8
18 de 18
si
se
incorpora
la
6) PROGRAMACIÓN LINEAL - ANÁLISIS POST-OPTIMAL
6.1) Un establecimiento que fabrica dos productos desea planificar su
producción haciendo máximo el margen de contribución a gastos
generales. Las restricciones con que cuenta son:
-Capacidad de despacho máxima 8.000 unidades (en conjunto de A y B)
-Capacidad de máquina: 540 hs. disponibles
Standard de A: 0,09 hs/unidad
Standard de B: 0,06 hs/unidad
-Producción mínima: 3.000 unidades (en conjunto de A y B)
-Cantidad demandada máxima: 5.000 unidades de A
6.000 unidades de B
Los márgenes de contribución unitarios son 60 $/unidad y 120 $/unidad
para los productos A y B respectivamente.
1. Resolver el problema gráficamente
2. Hallar gráficamente y graficar las variaciones de:
Funcional.
Producción de A y B.
Uso de despacho y horas de máquina cuando la cantidad
demandada máxima de B varía entre cero e infinito.
3. Ídem punto 2. cuando la restricción de producción mínima varía
entre cero e infinito
4. Ídem punto 2. cuando la disponibilidad de horas máquina varía
entre cero e infinito.
5. Determinar la curva de oferta del ítem A sabiendo que su costo
directo es 65$/unidad.
6.2) Dado el enunciado de un problema de programación lineal y las
tablas inicial y final de su resolución por el método simplex se pide:
a) Obtener el rango de variación del coeficiente C5 sin que cambie la
estructura de la solución óptima. Detallar los cálculos realizados.
b) Qué utilidad unitaria mínima deberá tener un producto P7 para que
sea conveniente producirlo, sabiendo que por unidad requiere 4 horas
hombre de mano de obra, 3 kilos de materia prima y no está incluido
dentro de la restricción de producción mínima
c) Graficar la variación de X2, Y2 y del funcional al variar la
disponibilidades del recurso materia prima entre 0 y 14 Kg por semana.
d) Determinar si altera o no la estructura de la solución óptima el
hecho de incorporar un nuevo proceso con coeficientes tecnológicos de
4,2,y 3 para A, B, y C respectivamente, con una disponibilidad de 11.
e) A qué valor total resulta conveniente vender a una empresa
interesada disponibilidades del recurso materia prima en una cantidad
de 4 kilos por semana.
f) Graficar la curva de oferta del producto B para C2 entre 0 y 100
Enunciado: Una empresa desea establecer el programa de producción para
sus tres productos A,B y C sujeto a las restricciones de producción
mínima (4 unidades por semana), disponibilidad de mano de obra (24
horas hombre por semana) y disponibilidad de materia prima (10 kilos
por semana). Los Cj son $ de utilidad.
19 de 19
Tabla inicial:
Ck
-M
Xk
U
X5
X6
Bk
4
24
10
Z = -4M
A1
A2
A3
1
1
1
1
4
2
1
2
4
-M-2
-M-8
-M-6
A2
A3
A4
A5
A6
-1
U
1
1
1
M
Tabla final:
Ck
Xk
Bk
8
X2
X5
X4
5
4
1
Z = 40
A1
0,5
-1
-0,5
2
1
2
-6
1
A4
A5
1
1
10
A6
U
0,5
-2
0,5
4
6.3) Dada una serie de datos de un problema de programación lineal y
las tablas inicial y final de su resolución por el método simplex se
pide:
a) Obtener el rango de variación del coeficiente C1 sin que cambie la
estructura de la solución óptima. Detallar los cálculos realizados.
b) Qué consumo máximo de horas hombre deberá tener un producto P7 para
que sea conveniente producirlo sabiendo que por unidad requiere 1Kg de
materia prima y tiene un beneficio unitario igual a 4.
c) Graficar la variación de X1, del valor marginal de la materia prima
y del funcional, al variar la disponibilidad del recurso horas hombre
entre cero y doce. Indicar el valor de las pendientes diciendo en qué
parte de la tabla se encuentran.
d) A qué valor total resulta conveniente vender a una fábrica
interesada 9 calorías.
e) Determinar si altera o no la estructura de la solución óptima el
hecho de incorporar un nuevo proceso para mejorar el resultado
operativo de los productos, (empaquetado) que requiere: 1,1, y 3
unidades de empaquetado por cada unidad de producto A, B, y C
respectivamente. Se disponen de 100 unidades de empaquetado por mes.
f) Graficar la curva de oferta del producto A cuando C1 varía entre 4 y
20.
DATOS:
R1 Horas hombre disponibles por mes :12
R2 Materia prima disponible por mes :12
R3 Calorías disponibles por mes
: 4
C1, C2, C3 Contribución marginal ($/unidad de producto)
X1, X2, X3 Unidades de productos A, B y C.
20 de 20
Tabla inicial
Ck
Xk
Bk
A1
A2
A3
A4
A5
A6
0
0
0
X4
X5
X6
12
12
4
2
1
1
1
2
-2
3
3
3
1
0
0
0
1
0
0
0
1
Z = 0
-4
-5
-6
0
0
0
4
4
8
1
0
0
0
1
0
1
1
4
2/3
-1/3
-4/3
Z = 36
0
0
3
1
Tabla final
4
5
0
X1
X2
X6
-1/3
2/3
5/3
2
0
0
1
0
6.4) Dado el enunciado de un problema de programación lineal y las
tablas inicial y final de su resolución por el método simplex se pide:
a) Obtener el rango de variación del coeficiente C1 sin que cambie la
estructura de la solución óptima.
b) Qué consumo máximo de vapor deberá tener un producto P7 para que
convenga fabricarlo si requiere 10 unidades de materia prima A, y 3 de
materia prima B, y tiene un beneficio unitario de $5.
c) Graficar la variación de X1, del valor del funcional, y del valor
marginal de la materia prima B cuando la disponibilidad de vapor varía
entre cero y 200. Indicar el valor de las pendientes señalando en qué
parte de la tabla se encuentran.
d) A qué valor total resulta conveniente vender a una empresa
interesada 25 unidades del recurso materia prima B.
e) Determinar si altera o no la estructura de la solución óptima el
hecho de incorporar un nuevo proceso (empaquetado) que requiere 2,3,y
15 unidades de empaquetado para cada unidad de producto 1,2, y 3
respectivamente. Se dispone de 100 unidades de empaquetado.
f) Graficar la curva de oferta del producto 3 entre los valores de C3
de 0 y 12.
Enunciado: Una empresa desea establecer su plan de producción para sus
tres productos 1, 2 y 3. Sujeto a restricciones de consumo mínimo de
materia prima A (24 Kg/día), disponibilidad máxima de materia prima B
(48 Kg/día) y consumo máximo de vapor
(24 Kg/día). Los Cj son $ de
contribución marginal.
21 de 21
Tabla inicial
Ck
3
4
2
0
0
0
-M
Bk
A1
A2
A3
A4
A5
A6
A7
24
48
24
2
6
-1
3
2
2
7
1,4
7
-1
0
0
0
1
0
0
0
1
1
0
0
-2M-3
-3M-4
-7M-2
M
0
0
0
96/7
24/7
24
0
1
0
1
0
0
456/7
0
0
Xk
M
0
0
u
X5
X6
Tabla final
4
3
0
X2
X1
X4
Z
=
31/10
-4/5
7/10
8
0
0
1
1/14
1/7
1/2
0
5/7
3/7
-1/7
1
9/7
0
0
-1
M
6.5) Dado el enunciado de un problema de programación lineal y las
tablas inicial y final de su resolución por el método simplex se pide:
a) Obtener el rango de variación del coeficiente C1 sin que cambie la
estructura de la solución óptima.
b) Qué utilidad unitaria mínima deberá tener un producto P7 para que
sea conveniente producirlo, sabiendo que por unidad requiere 2Kg de
materia prima A, y 3hs de máquina.
c) Graficar la variación de: la cantidad de producto 1, el valor
marginal del recurso hs de máquina, y el funcional, al variar la
disponibilidad de materia prima entre 8 y 30 Kg por día. Indicar el
valor de las pendientes señalando en qué parte de la tabla se
encuentran.
d) A qué valor total resulta conveniente vender a una empresa
interesada 12 unidades del recurso horas de máquina.
e) Determinar si altera o no la estructura de la solución óptima el
hecho de incorporar una nueva restricción sobre mano de obra. La
disponibilidad diaria es de 40 hs hombre, cada producto utiliza 5, 6 y
1 hs hombre respectivamente por cada unidad.
f) Graficar la curva de oferta del producto 2 entre los valores de C2 2
y 10.
Enunciado:
Una empresa fabrica y vende tres productos 1,2, y 3. Se dispone de 10Kg
diarios de materia prima y de 20hs de máquina diaria. Cada producto
requiere 1, 2 y 1 kg de materia prima respectivamente y 4, 2, y 2 hs de
máquina por unidad.
Debido a un contrato firmado con un cliente se debe producir como
mínimo 2 unidades diarias de producto 2.
22 de 22
Tabla inicial
Ck
Xk
Bk
A1
A2
A3
A4
A5
A6
A7
-M
X4
u
X6
10
2
20
1
0
4
2
1
2
1
0
2
1
0
0
0
-1
0
0
0
1
0
1
0
Z = -2M
-4
-M-3
-2
0
M
0
0
4/3
10/3
10/3
0
0
1
0
1
0
1/3
1/3
1/3
2/3
2/3
-1/3
1
0
0
-1/6
-1/6
1/3
Z = 70/3
0
0
1/3
2/3
0
5/6
Tabla final
0
3
4
X5
X2
X1
6.6) Para el ejercicio 3.1 se pide:
1.
2.
Definir las variables del problema (directo y dual).
Expresar la solución en términos de un programa de
producción, indicando el porcentaje de utilización de los
recursos.
3.
Determinar los valores marginales y los costos de oportunidad.
4.
Calcular el rango de variación de los coeficientes del
funcional y de los valores de las restricciones, dentro de
los cuales se conserva la estructura de la solución.
5.
Analizar la conveniencia de solicitar un aumento en la
provisión de lana tipo "M" si se sabe que dicho aumento
solo sería factible reduciendo la provisión de lana tipo
"N" a razón de 2Kg de merma en esta última por cada Kg
adicional de la primera. Por ejemplo si el proveedor
entregara 21 Kg de
"M" la entrega máxima de "N" sería de
34 Kg.
En caso de ser conveniente dicho aumento determinar:
a) Cual es el máximo beneficio adicional que puede
obtenerse
b)Cual sería la cantidad de lana de cada tipo a entregar semanalmente por cada proveedor.
c)Cual sería el reordenamiento de producción necesario para obtener
dicho beneficio máximo. Analizar el cambio a realizar en relación a
la utilización de las disponibilidades de los otros recursos.
d) Cuanto habría que aumentar el precio de los pulloverstipo "A"
para que su fabricación sea conveniente.
23 de 23
Las siguientes son las tablas primera y óptima del problema directo:
Ck
Xk
Bk
A1
A2
80
80
20
36
10
5
6
1,6
-M
X5
X6
X7
X8
U
Ck
Xk
Bk
A1
A4
1,8
1
A2
A5
A6
A7
A8
A9
U
-1
1
A9
U
1
4
X9 6,66 -0,5
1500 X3 3,33 -1,33
1800 X4 16,66 1,33
X8 6
0,9
1500 X2 13,33 0,83
Z=55000
A3
4
1,2
1
1
1,8
1
1
A3
A4
1
1
1
650
A5
A6
A7
0,166 0,250 -0,833
0,250 -0,833
0,833
-0,3 -0,45 1,5
0,166
250
375
A8
1
1
250
6.7) Una refinería de petróleo produce NAFTAS, GASOIL y FUELOIL. La
refinería puede funcionar bajo 3 modos diferentes de operación: A, B ó
C. La tabla que sigue muestra la cantidad de cada uno de los productos
que la refinería es capaz de producir (en miles de barriles / día) bajo
cada uno de los regímenes de operación. Se indican además, los márgenes
de beneficio de cada uno de los productos en $/bbl.
NAFTAS
GASOIL
FUELOIL
A
B
C
14
14
10
6
4
6
0
2
4
MARGEN
10
5
-2
Se desea programar la operación de la refinería para un mes de 30 días,
de modo de hacer máximo el margen de beneficio sabiendo que es
necesario abastecer el mercado de FUELOIL que demanda 20 mil
barriles/mes, y el de GASOIL que demanda 30 mil barriles/mes. El
mercado es capaz de tomar toda la oferta de NAFTAS sin deterioro en el
margen.
El problema ha sido planteado como uno de Programación Lineal de la
siguiente forma:
24 de 24
Z= 170 X1 + 156 X2 + 122 X3
6 X1 + 4 X2 + 6 X3 ≥
0 X1 + 2 X2 + 4 X3 ≥
1 X1 + 1 X2 + 1 X3 =
(MAX)
30
20
30
Se dan además las tablas inicial y final.
Tabla inicial:
Ck
Xk
Bk
A1
A2
A3
A4
A5
A6
A7
-M
-M
-M
0
u1
u2
u3
X7
30
20
30
30
6
0
1
1
4
2
1
1
6
4
1
1
-1
0
0
0
0
-1
0
0
0
0
-1
0
0
0
0
1
Tabla Final
Ck
Xk
Bk
A1
A2
A3
A4
A5
A6
A7
156
0
170
0
X2
X4
X1
X6
10
130
20
0
0
0
1
0
1
0
0
0
2
-4
-1
0
0
1
0
0
- ½
1
½
0
0
0
0
1
0
6
1
1
1) Describa el programa de producción óptimo. Principales variables y
unidades.
2)¿Cuánto GASOIL y FUELOIL se produce por encima del mínimo requerido?
3)¿Cómo variará el funcional si se incrementa en un día la operación
tipo C?
4)¿Qué beneficio o pérdida generará la reducción de los requerimientos
mínimos de FUELOIL en 1 unidad?
5)¿Qué variación sufriría el beneficio si el mes fuera de 31 días?
6)Graficar el valor del funcional, y de la producción de los 3
productos cuando la exigencia de la producción mínima de FUELOIL varía
entre 0 y 20 mil barriles/mes.
7)¿Es conveniente la instalación de un nuevo proceso D que es capaz de
producir 14 mil barriles/día de NAFTAS, 4 mil de GASOIL y 4 mil de
FUELOIL?
25 de 25
6.8)A continuación se dan el planteo, y las tablas inicial y final de
un problema de programación lineal:
Ck
Xk
0
X3
M
u1
M
u2
M
u3
Z = 5M
B
6
3
1
1
1
A1
1
1
1
0
2
A2
1
1
0
1
A3
1
0
0
0
A4
0
-1
0
0
A5
0
0
-1
0
A6
0
0
0
-1
Ck
1
2
0
0
Z =
B
2
1
3
1
1
A1
1
0
0
0
0
2
A2
0
1
0
0
0
A3
0
0
1
0
0
A4
-1
0
1
-1
-1
A5
0
0
0
1
0
A6
1
-1
0
1
-1
Xk
X1
X2
X3
X5
4
Restricción
Restricción
Restricción
Restricción
R1
R2
R3
R4
1) Indique los valores numéricos óptimos de las variables fuertes y
slack.
2) Calcule los rangos de variación de los coeficientes del funcional
dentro de los cuales no se altera la estructura de la solución óptima.
Explique qué entiende por “estructura de la solución óptima”.
3) ¿Cómo se modifican los valores de las variables básicas si la
restricción “R4” cambia de X2 ≥ 1 a X2 ≥ 0? ¿ Porqué puede asegurar que
las variables básicas siguen siéndolo ?
4) ¿ Qué efecto produciría en el valor del funcional disponer de una
unidad adicional de recurso “R1” ? - Explique porqué.
5) ¿ Qué efecto produciría en el valor del funcional modificar las
restricción “R2” a:
X1 + X2 ≥ 2 ? - Explique porqué.
6) Defina Valor Marginal de un recurso. Explique con un ejemplo sobre
la tabla óptima.
7) Defina Costo de Oportunidad de un producto. Explique con un ejemplo
sobre la tabla óptima.
8) Se incorpora al sistema un nuevo producto que utiliza 3 unidades de
recurso “R1” por unidad de producto. ¿ Cómo debe ser el coeficiente del
funcional para que no se altere la solución óptima ?
9) ¿ Se altera la solución óptima si se incorpora la restricción “R5”:
2 X1+X2 ≤ 6 ?
10) El término independiente de “R4” (b4) vale 1 en el problema dado.
Grafique el valor de X1, X2, Z y el valor marginal de “R4” cuando b4
varía entre 0 y 7.
6.9) A continuación se muestran las tablas inicial y final (directa y
dual) de un modelo lineal. Se dispone de $12, se puede comprar un
recurso o venderlo, pero no se pueden hacer ambas cosas al mismo
tiempo. Indicar qué es lo más conveniente y justificar la respuesta.
a) recurso 3: precio de compra $0,5 ; precio de venta $2,0
b) recurso 2: precio de compra $1,0 ; precio de venta $2,0
c) ambos recursos con los mismos precios de compra y venta que en los
dos puntos anteriores; no se puede comprar y vender un mismo recurso,
sí distintos.
26 de 26
Tabla inicial:
Ck
0
0
0
Z=0
Xk
X3
X4
X5
Bk
4
12
18
3
A1
1
0
3
-3
5
A2
0
2
2
-5
A3
1
0
0
A4
0
1
0
A5
0
0
1
A3
0
0
1
A4
-1/3
1/2
1/3
3/2
A5
1/3
0
-1/3
1
18
0
A3
A4
0 1/3
1 -1/3
0
-2
0
A5
-1/2
0
-6
Tabla óptima directa:
Ck
3
5
0
Xk
X1
X2
X3
Z=36
Bk
2
6
2
3
A1
1
0
0
5
A2
0
1
0
Tabla óptima dual:
Bk
12
18
Yk
Y2
Y3
Z=36
Ck
3/2
1
4
A1
-1/3
1/3
-2
12
A2
1
0
0
27 de 27
7) MODELOS DE INVENTARIO
7.1) Un comerciante realiza con un mayorista un contrato para la
provisión de 100.000 cajas en el término de 100 días hábiles a razón de
1.000 cajas por día. El límite de producción por día de trabajo es de
8.000 cajas; el fabricante puede destinar el tiempo disponible para la
fabricación de otros artículos de entrega diaria. El costo de
mantenimiento en stock es de 1$/unidad cada 25 días. El costo de
elaboración es de 15,15 $/unidad, el costo de la orden de producción
asciende a 320 $/orden. Se supone que el fabricante no tiene
restricciones de espacio para almacenamiento ni de disponibilidad de
capital.
a)Determinar el tamaño del lote óptimo.
b)Determinar el lapso que debe transcurrir entre dos órdenes de
producción sucesivas.
c)Calcular el costo total esperado óptimo de la operación.
d)Graficar el stock en función del tiempo
7.2) Una compañía manufacturera de aviones utiliza remaches a razón de
5.000 al año en forma aproximadamente constante.
Los remaches cuestan 2.000 $/unidad. El personal de la empresa estima
que cuesta $20.000 hacer un pedido de estos remaches y que el costo de
inventario es del 10% del valor de la pieza por año.
¿Con qué frecuencia deben hacerse pedidos de remaches y qué cantidades
deben ordenarse?
Si los costos reales son de $60.000 por hacer un pedido y el costo del
inventario es del 15% del valor de la pieza por año, el óptimo cambia.
¿Cuanto está perdiendo la empresa anualmente debido a una información
incorrecta sobre costos?
7.3)
Una
empresa
celebra
un
contrato
con
una
mutualidad
comprometiéndose a entregarle 120.000 Kg. de fideos a lo largo de un
año en forma uniforme. Se establece que en el caso de interrumpirse el
aprovisionamiento, se descontará al contratista de sus facturas, una
cantidad equivalente al 30% del precio de venta del producto por mes de
atraso siempre que la mora no exceda de 15 días. De sobrepasar este
límite, la multa será del 50% por mes de atraso. La empresa vende el
producto a $120 el Kg. y considera que la producción de un lote lleva
asociado un costo indirecto de $9.000. El costo de mantener almacenado
un Kg. de producto durante un año es de $60.
Se pide:
a) Calcular el tamaño del lote óptimo de producción.
b) Calcular el stock máximo óptimo que se acumulará.
c) Calcular el lapso óptimo entre tandas de producción y el lapso
durante el cual permanecerá agotado el producto.
d) Calcular el costo total esperado óptimo.
7.4) En el caso del problema anterior se desea evaluar el costo de
mantener un stock de protección de 500 unidades que serán entregadas al
comprador al finalizar el lapso acordado, por lo cual el stock de la
empresa manufacturera debe quedar en cero.
28 de 28
7.5) Un contratista tiene que proveer 10.000 cojinetes por día a una
fábrica de automóviles. Encuentra que cuando inicia un lote de
producción puede producir 25.000 cojinetes por día. El costo de
mantener un cojinete en stock por año es de $2, y el costo de arranque
de un lote de producción es de $1.800.
¿Con qué frecuencia debe fabricar los lotes de producción?
7.6) Un ítem con demanda mensual D = 2.000 unidades, costo de orden
$35.000 y tasa de interés 2% mensual, tiene la siguiente división de
precios:
≤
≤
≤
0
500
4.000
q ≤
500
q ≤ 4.000
q ≤ infinito
1.000
900
800
$/unidad
$/unidad
$/unidad
Se pide:
a)
b)
c)
d)
Representar la ley de precios
Determinar el lote óptimo
Calcular el CTE de la operación
Representar el CTE:f(q)
7.7) Un fabricante debe mantener 5 ítems en stock. Conoce sus demandas
anuales y costos unitarios respectivos, que se transcriben a
continuación:
ÍTEM
DEMANDA
PRECIO
1
2
3
4
5
1.000
2.000
4.000
10.000
1.000
$ 5
$ 10
$ 15
$ 5
$ 10
El costo de reorden es de $50 y la tasa de interés es del 10% anual.
Se desea saber:
a) El total inmovilizado en inventario (T.I.) medido en $ si su oficina
de compras procesa 50 órdenes por año adjudicándolas a razón de 10 por
ítem.
b) T.I. mínimo con asignación óptima de 50 órdenes.
c) T.O. mínimo para tener un T.I. de $9.000.
Calcular para todos los casos el tamaño de los respectivos lotes.
29 de 29
7.8) Un intermediario de productos elaborados debe mantener en stock
cantidades de uno de ellos con el objeto de satisfacer una demanda
definida. Resolver el problema con las siguientes consideraciones:
a)
b)
c)
d)
La no existencia de restricciones.
La existencia de una2 restricción de espacio máximo de
almacenamiento de 500 m .
La existencia de una restricción de dinero disponible por
vez para adquirir el lote de $250.000
La existencia simultánea de ambas restricciones.
Los datos del problema son:
DEMANDA
K
b
P
Superficie
7.000
500
200
2
5
u/mes ( constante)
$
$/u
%2 mensual
m /u
7.9) Una compañía fabrica dos productos P1 y P2 para los cuales sus
demandas mensuales se suponen aproximadamente constantes. Necesidades
de fabricación hacen que estas dos líneas de producción deban
elaborarse en lotes, deseándose operar al mínimo costo total.
Se conocen los costos directos de fabricación de cada producto y el
costo de puesta en marcha de fabricación de cada lote.
La compañía estima que el costo de almacenamiento de su producto es del
3% mensual del capital inmovilizado.
PRODUCTO 1
Demanda u/mes
Costo unitario $/u
Costo de reorden $/lote
PRODUCTO 2
420
7
500
550
23
120
Determinar:
a)Lotes económicos de fabricación de cada producto
b)Gráfico para cada línea de producción del CTE en función de los
distintos lotes a fabricar.
c)Gráfico de las curvas de isocosto de producción para distintos
pares de valores de lotes a fabricar.
d)Si se considera que la fábrica dispone como máximo de 300 lugares
de almacenamiento, y que cada unidad de P1 requiere 12 lugares y
cada unidad de P2, 18 se desea saber:
1)¿Cuáles son los nuevos lotes económicos a fabricar?
2)Comparar esta situación con la del punto a)
3)¿Cuánto se puede pagar por cada lugar de almacenamiento
que se alquile?
30 de 30
7.10) Una fábrica debe entregar todos los meses 1.200 unidades de un
cierto producto de su manufactura. Los pedidos se distribuyen
uniformemente a lo largo del tiempo. Razones de índole técnico obligan
a comenzar la producción una vez que se hayan acumulado pedidos por 400
unidades y por motivos económicos de producción, finaliza una vez
completado un lote igual a la demanda mensual.
La capacidad productiva de fábrica permite producir a razón de 120
unidades diarias. Existe un costo de almacenamiento de 50 $/unidad y
por día. Acondicionar las máquinas para comenzar a producir cuesta
$180.000. Todo otro gasto se considera despreciable y no se toma en
cuenta.
Se pide:
a)Graficar la función de stock
b)Calcular el costo operativo mensual
c)¿Cuál es la capacidad mínima que debe tener el depósito para
almacenar el producto?
7.11) Un comerciante recibe mercadería de un distribuidor con el cual
ha firmado el siguiente contrato: El comerciante pedirá un lote de
mercadería pero el distribuidor le entregará en forma instantánea la
mitad del lote pedido y el resto del lote al día siguiente.
El comerciante conoce la demanda (D) constante y el costo de mantener
un unidad almacenada (C), como también el costo (K) de ordenar un lote.
Se pide:
a)Graficar el stock en función del tiempo.
b)Plantear la función del costo total esperado.
c)Calcular el lote óptimo.
7.12) Una empresa que fabrica dos productos, A y B, desea fijar su
política de stock. Conoce la demanda anual de los mismos (32.000 y
135.000 unidades), que supone uniforme. Ha estimado en 10% anual el
costo de oportunidad del dinero inmovilizado en stock. Iniciar cada
tanda de producción implica costos de $1.000 y $5.000, respectivamente. Los costos unitarios de los productos son $40 para A y $60 para
B. Las velocidades de producción son tales que se puede suponer la
reposición como instantánea. No se desea tener demanda insatisfecha, ni
se llevará stock de protección.
Se pide determinar los lotes óptimos para ambos productos y el
valor marginal del recurso utilizado en cada uno de los
siguientes casos:
1
Los volúmenes requeridos
para almacenar cada unidad de
3
3
producto
son:
3
dm
y
5
dm
respectivamente,
se dispone de 15
m3 de depósito para los mismos.
2
Por razones de seguridad se decide que no puede haber (en
promedio), más de 10.000 unidades en stock entre los dos
productos.
3
El jefe de producción decide que no se hagan más de 7 tandas
de producción por año entre los dos productos.
4
Para obtener ventajas en la contratación del seguro se dispone
que el capital máximo inmovilizado en stock no debe exceder de
$600.000
31 de 31
5
6
7
8
9
10
11
La oficina de personal ha decidido reducir la mano de obra
indirecta y exige que no se dediquen más de 10 días anuales
(de 8 hs.) a preparar las máquinas para iniciar tandas de
producción. Cada tanda de A requiere 8 hs, cada una de B,6 hs.
El controller solicita que no exceda de $100.000 anuales el
costo de preparación.
La gerencia financiera dispone que no debe exceder de $40.000
el costo anual del capital promedio inmovilizado en stock.
Considere simultáneamente las restricciones 2 y 3.
Considere simultáneamente las restricciones 4 y 6.
Considere simultáneamente las restricciones 5 y 7.
Considere simultáneamente las restricciones 1 y 2.
7.13)
Resuélvase
nuevamente
el
problema
12
con
la
siguiente
modificación: no se supone que la reposición sea instantánea y se
conocen las respectivas velocidades de producción, 3.000 u/mes para A y
15.000 u/mes para B.
7.14)
Resuélvase
nuevamente
el
problema
12
con
la
siguiente
modificación: para el producto A se supone reposición instantánea y se
decide mantener un stock de protección igual al 5% de la demanda anual;
para el producto B, una velocidad de reposición de 15.000 u/mes y un
stock de protección igual al 10% del lote de producción.
7.15) Un almacén opera con dos productos para los que se conocen los
siguientes datos:
Demanda anual (constante)
Costo de reorden
Costo de almacenamiento
Costo unitario
Costo de oportunidad del dinero
Espacio ocupado
Reposición
PRODUCTO I
PRODUCTO II
182.500 u
500 $
0,5 $/u.día
10 $/u.
10 % anual
0,5 m2/unidad
Nota 1
365.000 u
750 $
0,5 $/u. día
12 $/u.
10 % anual
0,5 m2/unidad
Nota 2
Nota 1: Cuando se solicita un nuevo lote el proveedor entrega
inmediatamente la mitad del lote pedido y la otra mitad al día
siguiente.
Nota 2: Cuando se solicita un nuevo lote el proveedor entrega los
productos a una tasa de 4.000 u/día.
1)Desarrolle un modelo que le permita calcular los lotes de cada uno de
los productos de modo que el costo
total sea mínimo, sabiendo que
dispone de un espacio total de 500 m2.
2)¿Qué precio estaría dispuesto a pagar por 1 m2 adicional de espacio
de almacenamiento? Explique porqué.
32 de 32
3)¿Qué precio estaría dispuesto a pagar
por 500 m2 adicionales
2
espacio de almacenamiento? ¿y por 600 m ? Explique porqué.
de
4)Escriba las inecuaciones que utilizaría para incorporar al modelo las
siguientes restricciones:
a)
b)
c)
d)
Capital inmovilizado máximo inferior a...
Capital inmovilizado promedio inferior a...
Costo anual del capital inmovilizado inferior a...
El total de reórdenes inferior a...
5)Explique conceptualmente las condiciones necesarias de KUHN-TUCKER
para funciones sujetas a restricciones de desigualdad.
33 de 33
8) PROGRAMACIÓN POR CAMINO CRITICO
8.1) Indicar cuáles de las siguientes afirmaciones corresponden a una
red de flechas y cuales a una red de potenciales:
a)Las actividades están representadas por flechas.
b)La longitud de la flecha es proporcional a la duración de la
tarea.
c)No necesita actividades ficticias.
d)Las flechas sólo indican relaciones entre tareas.
e)Los nodos representan sucesos.
f)Los nodos representan tareas.
g)Pueden obtenerse a partir de matrices de precedencia.
h)Permiten el cálculo inmediato de Ft y FT de los sucesos de la
red.
8.2) Construir la red de relaciones lógicas correspondiente al
siguiente proyecto definido por las actividades, sus precedencias
inmediatas y sus duraciones. Calcular las fechas tempranas y tardías de
los nodos (sucesos). Calcular PFC, PFF, UFC, UFF de las actividades
(tareas). Identificar los nodos críticos, las actividades críticas y el
camino crítico. Expresar correctamente la duración total del proyecto.
Calcular los márgenes total, libre e independiente de tres actividades
no críticas de la red y graficarlas en una escala de tiempo.
ACTIVIDAD
A
B
C
D
E
F
G
H
I
J
PRECEDE
INMEDIATAMENTE A:
D
C
E
F
G
J
F
G
H
I
K
J
L
M
M
DURACIÓN
(semanas)
1
4
2
3
4
6
3
5
3
1
K
L
M
6
5
4
8.3) Ídem 8.2 para el siguiente proyecto:
ACTIVIDAD
PRECEDE
INMEDIATAMENTE
A:
DURACIÓN
(semanas)
A B C D E F G H Y J K L
M N
P Q R
S T V
B D B B E H G D
C
C
H E
F A
I
J J M
K
L Q P
V
8 8 6 5 4 8 6 6 3 4 6 12 1 12 4 6 12 5 6 4
34 de 34
8.4) Construir el diagrama calendario en Ft y PFC, y en FT y UFF para
la red del ejercicio 8.2
8.5) El proyecto a que hace referencia el ejercicio 8.2 se desea
acelerar reduciendo en 2 semanas su duración. Establecer qué
actividades deberán ser aceleradas y justificar los motivos. En caso de
faltarle información debe señalarlo especificando la razón.
Reconstruya la red y el camino crítico para la situación final que
obtenga. Clarifique correctamente su propuesta.
8.6) Para una actividad i-j de 4 semanas de duración se tiene
conocimiento de las siguientes fechas: Fti:10 FTi:21 Ftj:16 FTj:24
Graficar la situación y deducir si es posible que se cumpla. En caso
afirmativo señalar si debería haber por lo menos otra tarea emergente
de i u otra concurrente a j. En caso negativo especificar que cambio
debería hacerse para obtener un planteo correcto. En ambos casos
indicar si la actividad i-j es crítica.
8.7) Sea el proyecto dado por las actividades indicadas a continuación:
A precede inmediatamente a D y C, duración 7 semanas
B precede inmediatamente a E
duración 10 semanas
C precede inmediatamente a E
tiempo optimista 4 semanas
tiempo pesimista 12 semanas
tiempo más frecuente 5 semanas
D no precede a ninguna
duración 4 semanas
E no precede a ninguna
tiempo optimista 1 semana
tiempo pesimista 9 semanas
tiempo más frecuente 2 semanas
Construir la red de relaciones lógicas y determinar el camino crítico.
Establecer la naturaleza de la variable duración total del proyecto.
Calcular la probabilidad de cumplimiento de proyecto en 16 semanas.
Calcular la probabilidad de que el proyecto se cumpla en no más de 18
semanas.
8.8) Las siguientes son las actividades correspondientes a un proyecto.
Se da además de la duración y el costo total, las actividades a las que
ellas preceden inmediatamente.
35 de 35
ACTIVIDAD
A
B
C
D
E
F
G
H
I
J
K
PRECEDE
INMEDIATAMENTE A
DURACIÓN
(SEMANAS)
C
D
E
F
E
F
G F H
J
K
I
I
10
8
13
6
5
11
2
(*)
12
4
15
I
COSTO TOTAL
70
120
60
80
130
50
140
210
80
110
100
(*) tiempo optimista 3 semanas
tiempo pesimista 11 semanas
tiempo más frecuente 4 semanas
Se pide:
Construir la red de relaciones lógicas completa.
Sobre otro diagrama determinar las Ft y FT, determinar el camino
crítico.
Calcular todos los elementos para poder dibujar los diagramas de
presupuesto del proyecto en fecha temprana y en fecha tardía,
suponiendo que las tareas se pagan una vez finalizadas las mismas.
Dibujar superpuesta la ley de ingresos acumulados los que se producen
periódicamente a razón de $200.000 cada 10 semanas y al finalizar el
período respectivo.
Responder las siguientes preguntas:
El proyecto es viable con los recursos económicos disponibles. Si el
proyecto no fuera viable, que alternativas propondría.
Cuanto costaría el proyecto en cada caso.
36 de 36
9) TEORÍA DE COLAS
A continuación se dan 9 enunciados. Para cada uno de ellos se pide:
a)Enunciar las hipótesis para modelizar el sistema. Explicitar el valor
numérico, unidad, y significado de las variables utilizadas.
b)Definir los estados del sistema.
c)Construir el grafo de las tasas de transición.
d)Construir la matriz D de las tasas de transición y permanencia;
justificar el procedimiento para obtener los elementos de la diagonal.
e)Explicar por qué la ecuación que utiliza la matriz D no es suficiente
para obtener el vector de probabilidades de estado. Indicar que otra
ecuación es necesaria. Plantear la ecuación matricial que permite
calcular las probabilidades de estado, definiendo claramente las
expresiones que aparecen en ella. Explicar sin resolverla numéricamente
cómo se obtienen los valores de las incógnitas (probabilidades de
estado).
f)Plantear en función de las probabilidades de estado, las expresiones
que permiten calcular:
I
II
III
IV
V
VI
VII
VIII
IX
X
XI
XII
XIII
XIV
XV
Número promedio de clientes en el sistema.
Número promedio de clientes en la cola.
Número promedio de clientes en cada canal de atención.
Número promedio de clientes que ingresan al sistema por hora.
Número promedio de clientes que salen del sistema por hora.
Tiempo promedio que un cliente permanece en el sistema.
Tiempo promedio que un cliente permanece en la cola.
Tiempo promedio que un cliente permanece en cada canal de
atención.
Probabilidad de que un cliente llegue al sistema y sea
atendido de inmediato.
Probabilidad de que un cliente llegue al sistema y no pueda
ingresar por falta de espacio
Porcentaje del tiempo que el sistema está vacío.
Porcentaje del tiempo que el sistema está totalmente ocupado.
Porcentaje del tiempo que hay personas en cola.
Porcentaje del tiempo que cada canal de atención está en
actividad.
Porcentaje del tiempo que cada canal de atención no está
ocupado.
g) Si cuenta con los datos suficientes, plantear la expresión del
funcional que represente el beneficio obtenido por operar el sistema.
Suponer en todos los casos que el
régimen, que la distribución de la
unidad de tiempo es de tipo Poisson
servicio de los canales de atención
sistema se encuentra en estado de
cantidad de clientes arribados por
y que la distribución del tiempo de
es exponencial.
37 de 37
9.1) Una pequeña peluquería, instalada en una galería comercial,
funciona 8 horas diarias, 22 días por mes. Posee dos sillones para
cortar el pelo y dos sillas para esperar. Los clientes llegan en
promedio cada 15 minutos. Si las dos sillas están ocupadas no entran y
van a otra peluquería. Uno de los peluqueros realiza en promedio un
corte cada 20 minutos, el otro cada 30 minutos. El segundo es preferido
por los clientes, de modo que, estando ambos desocupados, el 80% opta
por cortarse con él. Cada corte de pelo se cobra $4. El sueldo de cada
peluquero es de $500.
9.2.) Resuelva el problema anterior suponiendo que no existe
preferencia por alguno de los peluqueros.
Explicite el significado matemático de la "indiferencia" por uno u otro
e interprételo frecuencialmente.
9.3.) Resuelva el primer problema suponiendo que cada uno
peluqueros tarda, en promedio 20 minutos para realizar un corte
y que no existe preferencia por uno u otro.
¿ Cree necesario definir como estados distintos un cliente
primer peluquero y un cliente con el segundo ? ¿ o es posible
un estado "un cliente cortándose" ?.
de los
de pelo
con el
definir
9.4.) Un cajero automático ubicado en el microcentro requiere, en
promedio, 3 minutos para ser utilizado. Sin embargo, el apuro de los
clientes y la proximidad de otros cajeros hace que ninguno se quede a
esperar si encuentra cuatro personas esperando. El 70% de quienes
encuentran 3 personas esperando tampoco se queda. Sólo el 40% de los
que encuentran dos personas esperando se incorpora a la cola, y el 30%
de los que encuentran una persona esperando se va. Sólo no se retiran
los que observan que no hay cola o lo encuentran desocupado.
9.5) Un lavadero automático cuenta con dos secciones: lavado (capacidad
de
atención
20
coches
por
hora,
en
promedio,
si
funciona
ininterrumpidamente) y secado (id. 30 coches por hora). El servicio se
cobra $400. Todo automóvil pasa consecutivamente por ambas etapas y no
se dispone de espacio para esperar entre ambas, sólo hay lugar para que
un coche espere antes del lavado. Los automóviles llegan, en promedio,
cada 2 minutos, el 20% de los que no puede atenderse de inmediato se va
a otro lavadero. Los costos de lavado y secado son $100 y $60 por hora
de funcionamiento, respectivamente.
¿Qué entiende por canal de atención bloqueado? ¿Puede bloquearse el
canal de secado?
9.6.) Resuelva el problema anterior suponiendo que el lugar
esperar se coloca entre los sectores de lavado y de secado.
¿Se bloqueará en algún caso el sector de lavado?
38 de 38
para
9.7.) Un taller mecánico está formado por tres sectores, cada uno
atendido por un operario: en el primero se desarma y revisa el
automóvil, en el segundo se lo repara y en el tercero se lo arma y se
controla el funcionamiento. No hay lugar para espera entre sectores
consecutivos, ni a la entrada. Los tiempos medios de atención son 30,
40 y 20 minutos, respectivamente. Los clientes llegan, en promedio cada
15 minutos. Cada servicio se cobra $200 (más repuestos) y el costo
horario de cada operario es de $20.
9.8.) En un pequeño local funciona una agencia de viajes. Los clientes
son atendidos por una recepcionista que confecciona una planilla con
sus datos y luego los deriva al vendedor de turismo internacional o de
turismo nacional, según su interés. Por hora llegan 10 clientes, en
promedio. Si observan una persona esperando ser atendido por la
recepcionista se van sin esperar. Una vez completada la planilla si el
vendedor correspondiente está desocupado el cliente pasa a ser atendido
por el mismo. Caso contrario para evitar que la espera lo impaciente y
se retire, la recepcionista le ofrece café y bombones y lo entretiene
conversando hasta que el vendedor se desocupe. El tiempo medio de
atención es de 4, 6 y 8 minutos para la recepcionista, el vendedor
nacional y el internacional respectivamente. Se ha comprobado que el
30% de los clientes está interesado en el turismo internacional.
9.9) Una estación de servicio ubicada en una ruta cuenta con un único
surtidor. Cada hora pasan, en promedio, 40 automóviles con la intención
de cargar, pero los conductores que observan algún automóvil esperando
no se detienen. La operación de carga dura un promedio de 3 minutos, a
continuación, el único empleado cobra el combustible. Si el pago se
realiza en efectivo demora, en promedio un minuto en cobrar. Si se paga
con tarjeta, el llenado de formularios y la verificación extienden el
período medio de cobro a tres minutos. La experiencia muestra que el
30% de los clientes paga con tarjeta.
Observe que, físicamente, el automóvil permanece en el surtidor durante
el pago, pero se puede construir el modelo imaginando que pasa a un
"canal de pago efectivo" o a un "canal de pago con tarjeta". El hecho
de que los tres canales sean atendidos por el mismo empleado ¿qué
restricción impone sobre el máximo de clientes que se encontrarán
simultáneamente en los canales?
39 de 39
10) SIMULACIÓN
EJERCICIOS PREVIOS
Método de la transformada inversa para variables discretas.
10.1) Se desea simular el conjunto de resultados obtenido al revolear
10 veces una moneda.
a)Grafique probabilidades y probabilidades acumuladas de los
eventos "cara" y "ceca".
b)Mediante el método de la transformada inversa defina un
procedimiento para generar cada resultado a partir de un número
aleatorio de distribución uniforme en el intervalo
0-1
("número al azar").
c)Tome un conjunto de 10 números al azar de una tabla y genere la
muestra.
10.2) Se desea simular las características de un conjunto de 20 señoras
que llegan a una peluquería. Se sabe que, en promedio, de cada diez
señoras que llegan, sólo 3 van a peinarse, 4 a cortarse el pelo y a
peinarse, 2 sólo a cortarse el pelo y 1 a hacerse la permanente. El
servicio requerido por cada una es independiente del requerido por las
otras. Siga los mismos pasos que en el 10.1.
10.3) Se desea simular la cantidad de llamados telefónicos que llegan a
una oficina en diez lapsos sucesivos de diez minutos cada uno. La
distribución de la cantidad de llamados es Poisson de media 1 llamado
cada 5 minutos.
a)Utilice la tabla que da, para una media a= λ .t, la probabilidad
de tener x o más llamadas G(x). Tenga presente
que el método de
la transformada inversa puede usarse también con G en lugar de F.
b)Defina el procedimiento para generar cada resultado (cantidad de
llamadas en 10 minutos) a partir de un número al azar.
c)Con un conjunto de diez números al azar tomados de la tabla,
genere la muestra.
Método de la transformada inversa para variable continua.
10.4) Una variable aleatoria está uniformemente distribuida en el
intervalo 2-6. Se desea generar una muestra de 5 valores de dicha
variable.
a)Defina y grafique f(x)
b)Defina y grafique F(x)
c)Aplique el método de la transformada inversa para obtener la
expresión que da el valor de la variable en función de un número
al azar.
d)Con un conjunto de cinco números al azar tomados de la tabla,
genere la muestra.
40 de 40
10.5) Ídem 4 para
una variable aleatoria cuya función de densidad está
dada por 3(x-1)2 en el intervalo 1-2 y 0 para los demás valores reales.
10.6) Ídem 4 y 5 para una3 variable aleatoria cuya función de densidad
está dada por (4/5)((x-3) ) en el intervalo 3-4 y -(2/5)(x-4)+ 4/5 en
el intervalo 4-6 y cero para los demás valores.
10.7) Ídem para la variable aleatoria cuya función de densidad es
triangular entre 1 y 4 con moda 3.
Para encontrar la expresión analítica f(x) tenga presente que f(3)
puede obtenerse sabiendo que el área total debajo de f(x) debe ser 1.
10.8) Un canal de un sistema de atención realiza el servicio en un
lapso cuya duración es una variable aleatoria continua exponencialmente
distribuida, con media igual a 10 minutos. Se desea generar una muestra
de 10 valores de los tiempos de servicio del canal.
a)Teniendo en cuenta que la función de densidad
de la distribución
(x)
para x>0, compruebe
exponencial tiene por expresión f(x)= µ .e µ
que la media (esperanza matemática) es 1/ µ y que la varianza es
1/ µ 2.
b)Aplique el método de la transformada inversa para hallar la
expresión del tiempo del servicio en función del número al azar.
c)Genere la muestra utilizando 10 números al azar tomados de la
tabla.
10.9) La llegada de clientes a un sistema de atención se produce según
un proceso de Poisson de parámetro λ =15 clientes/hora. Se desea
generar una muestra de los tiempos entre arribos de 5 clientes
sucesivos. Partiendo de una "hora inicial" arbitraria por ejemplo h=100
generar la "hora" de llegada de cada uno.
Recuerde que si la cantidad de clientes que llegan en un lapso dado
tiene distribución Poisson (DISCRETA), los tiempos entre arribos
sucesivos tienen distribución exponencial (CONTINUA), cuya función de
densidad está dada por f(x)= λ e(- λ x).
a)Repita los pasos del problema anterior para generar los tiempos
entre arribos.
b)Obtenga la "hora" de arribo de cada cliente. Observe que se la
puede obtener sumando a la hora inicial los lapsos hasta el
arribo del cliente dado.
c)¿Puede usarse el método b para generar las "horas" de
finalización de servicio de cada cliente en un canal de atención?
¿Por qué?
41 de 41
10.10) Las cantidades de un producto demandadas mensualmente a una
empresa se distribuyen normalmente con media 5.000 unidades y
desviación standard de 500 unidades. Se desea generar una muestra de
las demandas mensuales para un año de operación y con ellas obtener,
para cada mes, la demanda acumulada desde principio de año.
a)Explique por qué no puede aplicarse rigurosamente el método de
la transformada inversa. Si se dispone un método aproximado de
integración ¿Qué requisito debe cumplir la expresión obtenida
para que sea aplicable el método de la transformada inversa?
b)Explique cómo encararía la simulación por un camino alternativo,
usando una tabla de F(x) o de G(x) y aplicando el método de la
transformada inversa como si se tratase de una variable
discreta.
c)Para aplicar un tercer método basado en el teorema del límite
central:
Demuestre que una variable r, uniforme en (0,1), tiene media
1/2 y varianza 1/12.
Demuestre que la variable aleatoria que se obtiene sumando n
números al azar tiende, al crecer n, a una variable normal.
Obtenga su media y su varianza.
Obtenga la expresión estandarizada de la variable normal
hallada en b. Cada número obtenido por este procedimiento será
un "número aleatorio normal" rn, que puede considerarse
muestra de una variable normal de media 0 y varianza 1.
Estandarice la variable normal a simular e iguálela a rn:
despejando la variable se tendrá la expresión que permite
generar cada valor de la variable (demanda) en función de rn.
d)Un cuarto método se basa en utilizar tablas de desviaciones
normales, dan directamente valores al azar de una variable
normal estandarizada rn. Aplique el último paso del método dado
en c y, tomando números aleatorios normales de la tabla, genere
la muestra solicitada.
Intervalos de
simulación.
Confianza.
Determinación
del
número
de
pasos
de
la
10.11) Suponga que se ha realizado una simulación de la llegada de
clientes a un sistema de atención y que, eliminados los del
transitorio, se tienen los datos de 100 clientes para el estado de
régimen. Se quiere determinar el tiempo medio de permanencia en el
sistema, se ha obtenido el tiempo en el sistema para cada uno de los
clientes. La suma de los valores da 317,2 y la suma de los cuadrados de
las diferencias entre los valores individuales y la media es 28,3
a)Estime el valor del tiempo medio de permanencia en el sistema.
b)Obtenga un intervalo de confianza para la media del tiempo de
permanencia en el sistema con un nivel de significación del 10%
Determine el ancho del intervalo. Si este procedimiento se
reiterase muchas veces ¿En cuantos casos el intervalo incluiría
el "verdadero valor" de la media a estimar?
c)Si se desea un intervalo de confianza de ancho 0,06 ¿Cuántas
muestras adicionales se deberán obtener?
d)Id c. pero se desea que el ancho del intervalo sea el 10% del
valor de la variable estimada.
42 de 42
10.12) Se dispone de 30 datos obtenidos al azar de la cantidad promedio
de clientes en un sistema de atención en estado de régimen, la suma es
125 y la suma de las desviaciones cuadráticas es de 28,3.
a)Estime las media de la cantidad de clientes en el sistema.
b)Obtenga un intervalo de confianza con un nivel de significación
del 20% para la longitud del sistema. Calcule el ancho del
intervalo.
c)Determine el número de observaciones necesario para que el ancho
del intervalo sea del 10% del valor de la variable estimada.
EJERCICIOS DE SIMULACIÓN
10.13) Aplicaciones de la Simulación a problemas de colas
Los nueve enunciados de teoría de colas se usarán para ser encarados
por simulación, con las siguientes modificaciones para los tiempos del
servicio:
1
1er peluquero: tiempo de corte uniformemente distribuido entre 15 y
25 minutos.
2o. peluquero:2 íd normalmente distribuido con media 30 minutos y
varianza 9 min .
2
íd 1.
3
Sin modificaciones.
4
Triangular en el intervalo (2min,5min), la moda corresponde a 3
minutos.
5
Lavado: Función de densidad dada por (2/9)*(x-3) en (3;6)
Secado: Uniforme entre 1 y 3 minutos.
6
id 5.
7
1a etapa: exponencial de media 30 minutos.
2a etapa: normal de media 40 minutos y desviación standard 2
minutos.
3a etapa: triangular en (15;25), la moda corresponde a 25 minutos.
8
Recepcionista: constante=4 minutos.
Vendedor nacional: uniforme entre 5 y 7 minutos.
Vendedor internacional: exponencial de media 8 minutos.
9
Carga: 1,2 minutos más un lapso uniformemente distribuido entre 2 y
3 minutos.
Cobro en efectivo:
f(x)
1
2
43 de 43
4
Cobro con tarjeta:
f(x)
1
2
3
4
Para cada uno de los nueve enunciados debe construirse una tabla de
simulación que reproduzca el funcionamiento del sistema y permita
contestar todas las preguntas formuladas en el punto f) de la Guía de
Teoría de Colas. Se recomienda:
a)
Cada fila de la tabla contendrá los datos de un eventual cliente:
-Número al azar usado para generar la variable aleatoria.
-Lapso desde el arribo anterior, "horario" de llegada,
"horario" de entrada y de salida de cada canal y de la cola,
etc..
-Número al azar usado para cada "sorteo" y resultado del mismo
(si entra o no al sistema, si opta por un canal o por el otro,
si requiere cierto servicio, etc..)
-Indicadores que se calculan, para ese cliente, a partir de
los "horarios" registrados (tiempo en el sistema, en cola
etc..).
-Observaciones del estado del sistema (cantidad de clientes en
el sistema, en cola, canales ocupados, vacíos o bloqueados
etc...)
b)
Se darán, de manera explícita, las expresiones utilizadas para
generar las variables aleatorias detallando el método seguido y la
deducción completa.
c)
Se generarán los datos de la tabla para una totalidad de 5 a 10
clientes.
d)
Aunque los valores de la tabla se hayan obtenido de forma
intuitiva, se deberá dar un procedimiento general para calcularlos.
Ese
procedimiento
puede
darse
verbalmente,
pero
debe
ser
suficientemente preciso como para obtener los datos en todos los
casos posibles, sin error ni ambigüedad.
e)
Se calcularán todas las variables solicitadas en la Guía de Teoría
de colas punto f), usando los valores de la tabla y detallando los
procedimientos
de
cálculo.
Es
importante
explicitar
los
procedimientos porque los valores obtenidos con muestras tan
pequeñas no serán representativos.
f)
Se construirá un intervalo de confianza con nivel de significación
del 10% para el tiempo medio de permanencia en el sistema. Se
determinará el número de observaciones adicionales para obtener un
intervalo de ancho 0,1 minutos.
g)
Id. para la longitud del sistema. Determinar la cantidad de
observaciones necesarias para obtener un intervalo de confianza
cuyo ancho sea del 15% de la variable estimada.
44 de 44
10.14) El stock de cierto producto es administrado bajo los siguientes
parámetros:
Tamaño del lote de reposición:
4.000 unidades
Stock mínimo al inicio del día:
1.500 unidades
Demanda aleatoria con distribución triangular de:
Valor mínimo:
800 unidades/día
Moda:
1.000 unidades/día
Valor máximo: 1.500 unidades/día
Costo de almacenamiento: 0.04 $/unidad.día
Costo de reorden: $320
Simular la evolución diaria de los niveles de stock, construir un
intervalo de confianza para el costo diario.
¿Cómo procedería para calcular el tamaño óptimo del lote de reposición?
10.15) Se modifican las duraciones de las tareas del problema 8.7 de
modo que pasan a ser distribuciones de probabilidad triangulares con
los siguientes parámetros:
Actividad
A
B
C
D
E
Duración Mínima
5
3
3
3
1
Moda
7
10
5
4
2
Duración Máxima
8
20
12
12
9
Diseñar un procedimiento de simulación que permita calcular, para cada
una de las actividades, la probabilidad de resultar crítica.
45 de 45
SOLUCION A LOS PROBLEMAS DE PROGRAMACION LINEAL DE LOS CAPITULOS 1 Y 4
Las impresiones que siguen fueron obtenidas con el programa L.I.N.D.O. ( Linear, Interactive aNd Discrete Optimizer)
Problema 1.1 y 4.1
MAX 8 X1 + 3 X2
SUBJECT TO
2) X1 <= 3
3) X2 <= 6
4) 6 X1 + 4 X2 <= 36
END
LP OPTIMUM FOUND AT STEP
2
OBJECTIVE FUNCTION VALUE
1)
37.5000000
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
3.000000
4.500000
REDUCED COST
.000000
.000000
SLACK OR SURPLUS
.000000
1.500000
.000000
NO. ITERATIONS=
DUAL PRICES
3.500000
.000000
.750000
2
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
8.000000
INFINITY
3.000000
2.333333
ALLOWABLE
DECREASE
3.500000
3.000000
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
ALLOWABLE
RHS
INCREASE
DECREASE
3.000000
3.000000
1.000000
6.000000
INFINITY
1.500000
36.000000
6.000000
18.000000
46 de 46
Problema 1.2 y 4.2
MAX 5 X1 + 2 X2
SUBJECT TO
2) - 2 X1 + X2 <= 2
3) X1 - X2 <= 2
4) X1 + X2 <= 5
END
LP OPTIMUM FOUND AT STEP
2
OBJECTIVE FUNCTION VALUE
1)
20.5000000
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
3.500000
1.500000
REDUCED COST
.000000
.000000
SLACK OR SURPLUS DUAL PRICES
7.500000
.000000
.000000
1.500000
.000000
3.500000
NO. ITERATIONS=
2
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
5.000000
INFINITY
2.000000
3.000000
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
2.000000
INFINITY
2.000000
3.000000
5.000000
INFINITY
ALLOWABLE
DECREASE
3.000000
7.000000
ALLOWABLE
DECREASE
7.500000
5.000000
3.000000
47 de 47
Problema 1.3 y 4.3
MAX 5 X1 + 2 X2
SUBJECT TO
2) X2 <= 3
3) 4 X1 + 6 X2 <= 24
4) 4 X1 - 3 X2 <= 12
END
LP OPTIMUM FOUND AT STEP
2
OBJECTIVE FUNCTION VALUE
1)
22.6666700
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
4.000000
1.333333
REDUCED COST
.000000
.000000
SLACK OR SURPLUS
1.666667
.000000
.000000
NO. ITERATIONS=
DUAL PRICES
.000000
.638889
.611111
2
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
5.000000
INFINITY
2.000000
5.500000
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
3.000000
INFINITY
24.000000
15.000000
12.000000
12.000000
ALLOWABLE
DECREASE
3.666667
5.750000
ALLOWABLE
DECREASE
1.666667
12.000000
15.000000
48 de 48
Problema 1.4 y 4.4
MAX 5 X1 + 8 X2
SUBJECT TO
2) 6 X1 + 5 X2 <= 30
3) X2 >= 1
4) - 2 X1 + 2 X2 <= 6
END
LP OPTIMUM FOUND AT STEP
3
OBJECTIVE FUNCTION VALUE
1)
41.7272700
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
1.363636
4.363636
REDUCED COST
.000000
.000000
SLACK OR SURPLUS DUAL PRICES
.000000
1.181818
3.363636
.000000
.000000
1.045455
NO. ITERATIONS=
3
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
5.000000
4.600000
8.000000
INFINITY
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
30.000000
INFINITY
1.000000
3.363636
6.000000
6.000001
ALLOWABLE
DECREASE
13.000000
3.833333
ALLOWABLE
DECREASE
15.000000
INFINITY
12.333330
49 de 49
Problema 1.5 y 4.5
MAX 6 X1 + 2 X2
SUBJECT TO
2) X1 + X2 <= 300
3) 2.5 X1 + 4 X2 <= 1000
4) X2 = 200
5) X1 <= 200
END
LP OPTIMUM FOUND AT STEP
2
OBJECTIVE FUNCTION VALUE
1)
880.000000
VARIABLE
X1
X2
ROW
2)
3)
4)
5)
VALUE
80.000000
200.000000
REDUCED COST
.000000
.000000
SLACK OR SURPLUS
20.000000
.000000
.000000
120.000000
NO. ITERATIONS=
DUAL PRICES
.000000
2.400000
-7.600000
.000000
2
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
5
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
6.000000
INFINITY
2.000000
INFINITY
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
300.000000
INFINITY
1000.000000
50.000000
200.000000
50.000000
200.000000
INFINITY
ALLOWABLE
DECREASE
6.000000
INFINITY
ALLOWABLE
DECREASE
20.000000
200.000000
33.333330
120.000000
50 de 50
Problema 1.6 y 4.6
MAX - 2 X1 + 4 X2
SUBJECT TO
2) X2 <= 3
3) 4 X1 + 6 X2 <= 24
4) 2 X1 + 2 X2 >= 0
END
LP OPTIMUM FOUND AT STEP
1
OBJECTIVE FUNCTION VALUE
1)
12.0000000
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
.000000
3.000000
REDUCED COST
2.000000
.000000
SLACK OR SURPLUS
.000000
6.000000
6.000000
NO. ITERATIONS=
DUAL PRICES
4.000000
.000000
.000000
1
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
-2.000000
2.000000
4.000000
INFINITY
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
3.000000
1.000000
24.000000
INFINITY
.000000
6.000000
ALLOWABLE
DECREASE
INFINITY
4.000000
ALLOWABLE
DECREASE
3.000000
6.000000
INFINITY
51 de 51
Problema 1.7 y 4.7
MAX 4 X1 + 4 X2
SUBJECT TO
2) X1 <= 6
3) X1 + X2 <= 8
4) X1 + 2 X2 <= 12
END
LP OPTIMUM FOUND AT STEP
2
OBJECTIVE FUNCTION VALUE
1)
32.0000000
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
4.000000
4.000000
REDUCED COST
.000000
.000000
SLACK OR SURPLUS
2.000000
.000000
.000000
NO. ITERATIONS=
DUAL PRICES
.000000
4.000000
.000000
2
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
4.000000
.000000
4.000000
4.000000
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
6.000000
INFINITY
8.000000
1.000000
12.000000
4.000000
ALLOWABLE
DECREASE
2.000000
.000000
ALLOWABLE
DECREASE
2.000000
2.000000
2.000000
52 de 52
Problema 1.8 y 4.8
MAX 6 X1 + 4 X2
SUBJECT TO
2) 2 X1 + 4 X2 <= 48
3) 4 X1 + 2 X2 <= 60
4) 3 X1 <= 45
END
LP OPTIMUM FOUND AT STEP
2
OBJECTIVE FUNCTION VALUE
1)
96.0000000
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
12.000000
6.000000
REDUCED COST
.000000
.000000
SLACK OR SURPLUS DUAL PRICES
.000000
.333333
.000000
1.333333
9.000000
.000000
NO. ITERATIONS=
2
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
ALLOWABLE
COEF
INCREASE
DECREASE
6.000000
2.000000
4.000000
4.000000
8.000000
1.000000
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
48.000000
72.000000
60.000000
9.000000
45.000000
INFINITY
ALLOWABLE
DECREASE
18.000000
36.000000
9.000000
53 de 53
Problema 1.9 y 4.9
MAX 2 X1 + X2
SUBJECT TO
2) - 5 X1 + 3 X2 >= 5
3) X1 + X2 <= 4
4) 2 X1 + X2 >= 10
END
NO FEASIBLE SOLUTION AT STEP 2
SUM OF INFEASIBILITIES= 5.12500
VIOLATED ROWS HAVE NEGATIVE SLACK,
OR(EQUALITY ROWS) NONZERO SLACKS.
ROWS CONTRIBUTING TO INFEASIBILITY HAVE
NONZERO DUAL PRICE.
OBJECTIVE FUNCTION VALUE
1)
4.87500000
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
.875000
3.125000
REDUCED COST
.000000
.000000
SLACK OR SURPLUS
.000000
.000000
-5.125000
NO. ITERATIONS=
DUAL PRICES
-.125000
1.375000
-1.000000
2
54 de 54
Problema 1.10 y 4.10
MAX X1 + 8 X2
SUBJECT TO
2) X2 >= 2
3) 4 X1 + 6 X2 >= 24
4) 10 X1 - 30 X2 >= 30
END
UNBOUNDED SOLUTION
UNBOUNDED VARIABLES ARE:
SLK 4
SLK 3
X1
OBJECTIVE FUNCTION VALUE
1)
25.0000000
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
9.000000
2.000000
REDUCED COST
.000000
.000000
SLACK OR SURPLUS
.000000
24.000000
.000000
NO. ITERATIONS=
DUAL PRICES
11.000000
.000000
.100000
3
55 de 55
Problema 1.11 y 4.11
MIN X1 - 2 X2
SUBJECT TO
2) X1 >= 2
3) 2 X1 + X2 <= 10
4) X1 + 2 X2 <= 8
5) X2 >= 1
END
LP OPTIMUM FOUND AT STEP
3
OBJECTIVE FUNCTION VALUE
1)
-4.00000000
VARIABLE
X1
X2
ROW
2)
3)
4)
5)
VALUE
2.000000
3.000000
REDUCED COST
.000000
.000000
SLACK OR SURPLUS DUAL PRICES
.000000
-2.000000
3.000000
.000000
.000000
1.000000
2.000000
.000000
NO. ITERATIONS=
3
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
5
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
1.000000
INFINITY
-2.000000
2.000000
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
2.000000
2.000000
10.000000
INFINITY
8.000000
6.000000
1.000000
2.000000
ALLOWABLE
DECREASE
2.000000
INFINITY
ALLOWABLE
DECREASE
2.000000
3.000000
4.000000
INFINITY
56 de 56
Problema 1.12 y 4.12
MAX 3 X1 + X2
SUBJECT TO
2) X1 + X2 <= 6
3) 2 X1 + 3 X2 <= 1
4) - X1 + 2 X2 >= 8
END
NO FEASIBLE SOLUTION AT STEP 1
SUM OF INFEASIBILITIES= 7.33333
VIOLATED ROWS HAVE NEGATIVE SLACK,
OR(EQUALITY ROWS) NONZERO SLACKS.
ROWS CONTRIBUTING TO INFEASIBILITY HAVE
NONZERO DUAL PRICE.
OBJECTIVE FUNCTION VALUE
1)
.333333300
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
.000000
.333333
REDUCED COST
2.333333
.000000
SLACK OR SURPLUS DUAL PRICES
5.666667
.000000
.000000
.666667
-7.333333
-1.000000
NO. ITERATIONS=
1
57 de 57
Problema 1.13 y 4.13
MAX 3 X1 + X2
SUBJECT TO
2) 2 X1 + X2 <= 8
3) X1 + X2 <= 6
4) X1 <= 4
END
LP OPTIMUM FOUND AT STEP
1
OBJECTIVE FUNCTION VALUE
1)
12.0000000
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
4.000000
.000000
REDUCED COST
.000000
.500000
SLACK OR SURPLUS DUAL PRICES
.000000
1.500000
2.000000
.000000
.000000
.000000
NO. ITERATIONS=
1
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
3.000000
INFINITY
1.000000
.500000
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
8.000000
.000000
6.000000
INFINITY
4.000000
INFINITY
ALLOWABLE
DECREASE
1.000000
INFINITY
ALLOWABLE
DECREASE
8.000000
2.000000
.000000
58 de 58
SOLUCION A LOS PROBLEMAS DE PROGRAMACION LINEAL DEL CAPITULO 6
Las impresiones que siguen fueron obtenidas con el programa L.I.N.D.O. ( Linear, Interactive aNd Discrete Optimizer)
Problema 6.1
MAX 60 X1 + 120 X2
SUBJECT TO
2) X1 + X2 <= 8000
3) 0.09 X1 + 0.06 X2 <= 540
4) X1 + X2 >= 3000
5) X1 <= 5000
6) X2 <= 6000
END
LP OPTIMUM FOUND AT STEP 4
OBJECTIVE FUNCTION VALUE
1)
840000.000
VARIABLE
X1
X2
VALUE
2000.000000
6000.000000
REDUCED COST
.000000
.000000
ROW
SLACK OR SURPLUS DUAL PRICES
2)
.000000
60.000000
3)
.000008
.000000
4)
5000.000000
.000000
5)
3000.000000
.000000
6)
.000000
60.000000
NO. ITERATIONS=
4
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
5
6
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
60.000000
60.000000
120.000000
INFINITY
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
8000.000000
.000090
540.000000
INFINITY
3000.000000
5000.000000
5000.000000
INFINITY
6000.000000
2000.000000
ALLOWABLE
DECREASE
60.000000
60.000000
ALLOWABLE
DECREASE
2000.000000
.000008
INFINITY
3000.000000
.000270
59 de 59
Problema 6.2
MAX 2 X1 + 8 X2 + 6 X3
SUBJECT TO
2) X1 + X2 + X3 >= 4
3) X1 + 4 X2 + 2 X3 <= 24
4) X1 + 2 X2 + 4 X3 <= 10
END
LP OPTIMUM FOUND AT STEP
3
OBJECTIVE FUNCTION VALUE
1)
40.0000000
VARIABLE
X1
X2
X3
ROW
2)
3)
4)
VALUE
.000000
5.000000
.000000
REDUCED COST
2.000000
.000000
10.000000
SLACK OR SURPLUS DUAL PRICES
1.000000
.000000
4.000000
.000000
.000000
4.000000
NO. ITERATIONS=
3
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
X3
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
2.000000
2.000000
8.000000
INFINITY
6.000000
10.000000
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
4.000000
1.000000
24.000000
INFINITY
10.000000
2.000000
ALLOWABLE
DECREASE
INFINITY
4.000000
INFINITY
ALLOWABLE
DECREASE
INFINITY
4.000000
2.000000
60 de 60
Problema 6.3
MAX 4 X1 + 5 X2 + 6 X3
SUBJECT TO
2) 2 X1 + X2 + 3 X3 <= 12
3) X1 + 2 X2 + 3 X3 <= 12
4) X1 - 2 X2 + 3 X3 <= 4
END
LP OPTIMUM FOUND AT STEP
2
OBJECTIVE FUNCTION VALUE
1)
36.0000000
VARIABLE
X1
X2
X3
ROW
2)
3)
4)
VALUE
4.000000
4.000000
.000000
REDUCED COST
.000000
.000000
3.000000
SLACK OR SURPLUS DUAL PRICES
.000000
1.000000
.000000
2.000000
8.000000
.000000
NO. ITERATIONS=
2
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
X3
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
4.000000
6.000000
5.000000
3.000000
6.000000
3.000000
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
12.000000
6.000000
12.000000
12.000000
4.000000
INFINITY
ALLOWABLE
DECREASE
1.500000
3.000000
INFINITY
ALLOWABLE
DECREASE
6.000000
4.800000
8.000000
61 de 61
Problema 6.4
MAX 3 X1 + 4 X2 + 2 X3
SUBJECT TO
2) 2 X1 + 3 X2 + 7 X3 >= 24
3) 6 X1 + 2 X2 + 1.4 X3 <= 48
4) - X1 + 2 X2 + 7 X3 <= 24
END
LP OPTIMUM FOUND AT STEP
4
OBJECTIVE FUNCTION VALUE
1)
65.1428600
VARIABLE
X1
X2
X3
ROW
2)
3)
4)
VALUE
3.428571
13.714290
.000000
REDUCED COST
.000000
.000000
8.000001
SLACK OR SURPLUS DUAL PRICES
24.000000
.000000
.000000
.714286
.000000
1.285714
NO. ITERATIONS=
4
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
X3
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
3.000000
9.000000
4.000000
INFINITY
2.000000
8.000001
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
24.000000
24.000000
48.000000
INFINITY
24.000000
24.000000
ALLOWABLE
DECREASE
5.000000
2.580646
INFINITY
ALLOWABLE
DECREASE
INFINITY
24.000000
24.000000
62 de 62
Problema 6.5
MAX 4 X1 + 3 X2 + 2 X3
SUBJECT TO
2) X1 + 2 X2 + X3 <= 10
3) X2 >= 2
4) 4 X1 + 2 X2 + 2 X3 <= 20
END
LP OPTIMUM FOUND AT STEP
3
OBJECTIVE FUNCTION VALUE
1)
23.3333300
VARIABLE
X1
X2
X3
ROW
2)
3)
4)
VALUE
3.333333
3.333333
.000000
REDUCED COST
.000000
.000000
.333333
SLACK OR SURPLUS
.000000
1.333333
.000000
NO. ITERATIONS=
DUAL PRICES
.666667
.000000
.833333
3
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
X3
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
4.000000
2.000000
3.000000
5.000000
2.000000
.333333
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
10.000000
9.999999
2.000000
1.333333
20.000000
8.000000
ALLOWABLE
DECREASE
1.000000
1.000000
INFINITY
ALLOWABLE
DECREASE
2.000000
INFINITY
9.999999
63 de 63
Problema 6.6
MAX 1000 X1 + 1500 X2 + 1500 X3 + 1800 X4
SUBJECT TO
2) 1.6 X1 + 1.2 X4 <= 20
3) 1.8 X2 + 1.8 X3 <= 36
4) 5 X1 + 6 X2 <= 80
5) 4 X3 + 4 X4 <= 80
6) X2 + X3 >= 10
END
LP OPTIMUM FOUND AT STEP 4
OBJECTIVE FUNCTION VALUE
1)
55000.0000
VARIABLE
VALUE
REDUCED COST
X1
.000000
650.000000
X2
13.333330
.000000
X3
3.333334
.000000
X4
16.666670
.000000
ROW
SLACK OR SURPLUS DUAL PRICES
2)
.000000
250.000000
3)
6.000000
.000000
4)
.000000
250.000000
5)
.000000
375.000000
6)
6.666667
.000000
NO. ITERATIONS=
4
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
X3
X4
ROW
2
3
4
5
6
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
1000.000000
650.000000
1500.000000
INFINITY
1500.000000
300.000000
1800.000000
INFINITY
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
20.000000
4.000001
36.000000
INFINITY
80.000000
20.000000
80.000000
13.333330
10.000000
6.666667
ALLOWABLE
DECREASE
INFINITY
779.999900
1500.000000
300.000000
ALLOWABLE
DECREASE
4.000000
6.000000
40.000000
13.333340
INFINITY
64 de 64
Problema 6.7
MAX 170 X1 + 156 X2 + 122 X3
SUBJECT TO
2) 6 X1 + 4 X2 + 6 X3 >= 30
3) 2 X2 + 4 X3 >= 20
4) X1 + X2 + X3 = 30
END
LP OPTIMUM FOUND AT STEP
4
OBJECTIVE FUNCTION VALUE
1)
4960.00000
VARIABLE
X1
X2
X3
ROW
2)
3)
4)
VALUE
20.000000
10.000000
.000000
REDUCED COST
.000000
.000000
20.000000
SLACK OR SURPLUS DUAL PRICES
130.000000
.000000
.000000
-7.000000
.000000
170.000000
NO. ITERATIONS=
4
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
X3
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
170.000000
20.000000
156.000000
14.000000
122.000000
20.000000
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
30.000000
130.000000
20.000000
40.000000
30.000000
INFINITY
ALLOWABLE
DECREASE
14.000000
10.000000
INFINITY
ALLOWABLE
DECREASE
INFINITY
20.000000
20.000000
65 de 65
Problema 6.8
MIN X1 + 2 X2
SUBJECT TO
2) X1 + X2 <= 6
3) X1 + X2 >= 3
4) X1 >= 1
5) X2 >= 1
END
LP OPTIMUM FOUND AT STEP
3
OBJECTIVE FUNCTION VALUE
1)
4.00000000
VARIABLE
X1
X2
ROW
2)
3)
4)
5)
VALUE
2.000000
1.000000
REDUCED COST
.000000
.000000
SLACK OR SURPLUS
3.000000
.000000
1.000000
.000000
NO. ITERATIONS=
DUAL PRICES
.000000
-1.000000
.000000
-1.000000
3
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
5
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
1.000000
1.000000
2.000000
INFINITY
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
6.000000
INFINITY
3.000000
3.000000
1.000000
1.000000
1.000000
1.000000
ALLOWABLE
DECREASE
1.000000
1.000000
ALLOWABLE
DECREASE
3.000000
1.000000
INFINITY
1.000000
66 de 66
Problema 6.9
MAX 3 X1 + 5 X2
SUBJECT TO
2) X1 <= 4
3) 2 X2 <= 12
4) 3 X1 + 2 X2 <= 18
END
LP OPTIMUM FOUND AT STEP
2
OBJECTIVE FUNCTION VALUE
1)
36.0000000
VARIABLE
X1
X2
ROW
2)
3)
4)
VALUE
2.000000
6.000000
REDUCED COST
.000000
.000000
SLACK OR SURPLUS DUAL PRICES
2.000000
.000000
.000000
1.500000
.000000
1.000000
NO. ITERATIONS=
2
RANGES IN WHICH THE BASIS IS UNCHANGED
VARIABLE
X1
X2
ROW
2
3
4
OBJ COEFFICIENT RANGES
CURRENT
ALLOWABLE
COEF
INCREASE
3.000000
4.500000
5.000000
INFINITY
RIGHTHAND SIDE RANGES
CURRENT
ALLOWABLE
RHS
INCREASE
4.000000
INFINITY
12.000000
6.000000
18.000000
6.000000
ALLOWABLE
DECREASE
3.000000
3.000000
ALLOWABLE
DECREASE
2.000000
6.000000
6.000000
67 de 67