Esbozos de econometría financiera

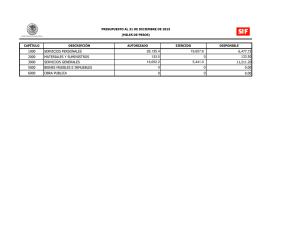
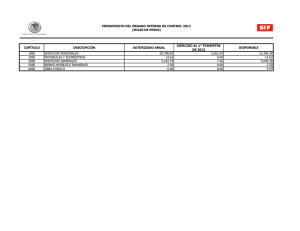
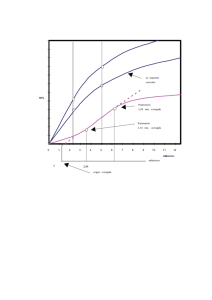
E CONOMÍA Y DESARROLLO
V O L U M E N 4FINANCIERA
N Ú M E R O 1, M A R Z O 2005
ESBOZOS DE,ECONOMETRÍA
37
Esbozos de econometría financiera
ELÍAS MORÉ OLIVARES*
Resumen
Este artículo presenta una aplicación práctica de la econometría financiera,
calculando la línea de mercado de capitales y determinando la validez del
modelo de evaluación de activos de capital a pesar de los supuestos de
competencia perfecta y los problemas relacionados con la beta histórica
planteados recientemente. El ejercicio teórico-práctico muestra cómo a pesar
de las discusiones, el MVAC sigue siendo un marco de trabajo, lógica y útil
conceptual y operativamente para relacionar riesgo-rendimiento.
Abstract
This article presents a practical application of the financial econometric,
measuring the line of capital market and determining the veracity of the
evaluation of the capital assets model never the less the supposed of perfect
competition and the problems related with the historic b recently formulated.
This theorical practical exercise shows how agnoledge of the decision the CAPM
continues being a logical and useful work frame conceptually and operatively
for relating risk and revenue.
Palabras clave: econometría financiera, riesgo, rendimiento, modelo de
valuación de activos de capital.
Clasificación JEL: C1, G13, G11
*
Economista. Magíster en Administración de Empresas y Magíster en Estudios Político-Económicos. Universidad
del Norte, de Barranquilla. Diplomado en Docencia Universitaria y Diplomado en Finanzas. Decano Facultad
de Ciencias Económicas Administrativas y Contables, Universidad Autónoma de Colombia. Las sugerencias
y comentarios serán recibidas al e-mail: decaecso@fuac.edu.co o al teléfono (571) 2860642 de Bogotá. Fecha de
recepción: 18 de febrero de 2005. Fecha de aceptación: 15 de marzo de 2005.
Universidad Autónoma de Colombia
38
ELÍAS MORÉ OLIVARES
1. Introducción
La metodología utilizada para el presente artículo es resaltar los aspectos
técnicos del modelo, explicar lo relevante de la teoría del riesgo-rendimiento
para posteriormente aplicarlo a un caso particular con el propósito de no
desvirtuar apresuradamente el modelo de valuación de activos de capital (MVAC).
Aunque no se utilizaron paquetes econométricos para mejorar el proceso
operativo, se utilizó álgebra matricial.
La econometría es una disciplina que mezcla la estadística y las matemáticas con la teoría económica para cuantificar fenómenos económicos y verificar teorías económicas, aplicando métodos particulares basados en la inferencia estadística.
La estrategia del econometrista es el siguiente proceso secuencial:
1.
2.
3.
4.
5.
6.
7.
8.
Planteamiento de la teoría o hipótesis.
Especificación del modelo matemático de la teoría.
Especificación del modelo econométrico de la teoría.
Obtención de datos.
Estimación de los parámetros del modelo econométrico.
Prueba de hipótesis.
Pronóstico o predicción.
Utilización del modelo para fines de control o de política.
De todo lo anterior, el modelo1 econométrico nos permite analizar cómo una
serie de variables explicativas afectan a la variable de interés para el analista
(a explicar) (MARTIN, LABEAGA y MOCHON, 1997; GUJARATI, 1990).
En los últimos años el rápido crecimiento de la moderna teoría financiera y
el desarrollo del proceso informático han permitido el uso de técnicas
econométricas en economía financiera dando lugar a la econometría financiera.
En este ensayo analizamos el modelo básico y realizamos una aplicación
práctica de la econometría financiera, área de estudio, que debe ser incluida en el currículo de formación del contador, administrador de empresas y
especialista en finanzas. Este cambio en el micro y macrodiseño curricular
es necesario porque el nuevo paradigma de la globalización, exige que los
profesionales en finanzas sean más competitivos, es decir, puedan realizar
investigaciones y tomar decisiones de la forma más exacta. Todo esto sería
posible con buenas bases matemáticas, estadísticas y epistemológicas que
1
Un modelo es una representación simplificada de la realidad que recoge los aspectos fundamentales de la misma
que tiene interés para los objetivos del investigador o analista.
Economía y Desarrollo - marzo 2005, vol. 4, n° 1
ESBOZOS DE ECONOMETRÍA FINANCIERA
39
faciliten comprender teorías financieras y aplicar los modelos ofrecidos por
la econometría financiera.
2. Modelo econométrico básico
El punto de partida de cualquier estudio econométrico es el planteamiento de
los objetivos finales del trabajo, para lo cual elegiremos un modelo derivado
de la teoría económica, capaz de cubrir los objetivos planteados. El paso del
modelo teórico al modelo econométrico genera una diferencia, cuyo
componente aleatorio, se registra en la ecuación de regresión y = g(X) + u,
donde u es la parte aleatoria no explicada por X (GUJARATI, 1990).
En la realidad no existen modelos exactos o determinísticos sino estocásticos
incluyendo una variable aleatoria con distribución probabilística. La función a estimar tiene la forma: y = βo + β1X + u.
En la práctica se trabaja con una muestra de tamaño n, extraída de la población, no siendo posible obtener βo y β1, sino una estimación (βo, β1) y logrando la regresión muestral mediante Yi = βo + β1 + e, donde yi es la variable a
explicar, X la explicativa, βo la ordenada en el origen y B1 la pendiente de la
recta de regresión.
Como ocurre en los modelos de dos y tres variables, en el caso de K variables
los estimadores de MCO se obtienen minimizando ∑e12, equivalente a minimizar e’e, puesto que:
e1
e’e = e1 e2.... en
e2
= e12 + e22 +... en2 = ∑e12
en
como Y = Xβ + e
e = y - Xβ
e’e = (Y-Xβ)’(Y-Xβ)
= y’y – y’Xβ-(Xβ)’y + (Xβ)’(Xβ)
por transposición de matrices (Xβ)’ = β’X’
como (β’X’y) es un escalar, es igual a su transpuesta y’Xβ, entonces:
e’e
= y’y - β’X’y - β’X’y + (Xβ)’(Xβ)
= y’y - 2β’X’y + β’X’X β
ϑ(e’e’)
diferenciando matricialmente ————— = -2X’y + 2X’Xβ
ϑβ
Universidad Autónoma de Colombia
40
ELÍAS MORÉ OLIVARES
igualando a cero 0 = 2X’y + 2X’Xβ.
-2X’Xβ = - 2X’y
X’Xβ = X’y
Para estimar los parámetros β1, β2,... Bk, el número de observaciones mínimo n que necesitamos ha de ser igual o mayor que el número de parámetros
a estimar (k) y el principio de los mínimos cuadrados ordinarios (MCO) es
idéntico para el modelo de regresión lineal y el de regresión múltiple.
Partiendo de β = (X’X)-1 X’y, (X’X) β = X’y
Para exponer el funcionamiento del cálculo matricial en forma elemental,
suponemos que el modelo a estimar tiene una sola variable explicativa (GREEN,
1998): Yi = β1 + β2Xi + Ui. Así,
X=
1 X1
1 X2
.
.
1 Xi
.
.
.
1 Xn
de manera que
1
1 ... 1
X1
X2 ... Xn
1 X1
1 X2 =
.
.
.
1 Xn
X’X =
Como el vector β es igual a β =
y
X’y =
1
1 1
X1 X2 Xn
Y1
Y2
.
.
n
∑Xi
∑Xi
∑Xi2
β1
β2
=
∑Y1
∑X1Y1
.
Yn
Economía y Desarrollo - marzo 2005, vol. 4, n° 1
41
ESBOZOS DE ECONOMETRÍA FINANCIERA
Para las n observaciones, el modelo puede ser descrito de la manera siguiente:
Y1 =
Y2 =
β1 + β2X21 + β3X31 +... βkXK1 + U1
β1 + β2X22 + β3X32 +... βkXk2 + U2
Yn =
β1 + β2X2n + β3X3n +... βkXkn + Un
•
•
•
La forma matricial detallada, de ese modelo lineal de regresión múltiple es:
Y1
Y2
.
.
.
Yn
1
1
.
.
.
1
=
X21
X22
X2n
Nx1
X3n . . . Xkn
β1
β2
.
.
.
βk
Nxk
Kx1
X31 . . . Xk1
X32 . . . Xk2
+
U1
U2
.
.
.
Un
Nx1
La forma matricial condensada del modelo es y = Xβ + u, equivalente al
modelo lineal Yi = βi + β2X2i + β3X3i +... βkxki + Ui, siendo
Y=
Y1
Y2
.
.
.
Yn
; X=
1
X21
1
X22
.
X= .
.
1
X2n
X31 . . . Xk1
X32 . . . Xk2
X3n . . . Xkn
β1
β2
.
. =
; β = ; β =; u
.
βn
Tenemos en notación matricial detallada
n
∑Xi
∑Xi
∑Xi2
β1
β2
=
∑Yi
∑XiYi
que recoge en forma matricial, las ecuaciones siguientes:
Universidad Autónoma de Colombia
U1
U2
.
; u=
.
Un
42
ELÍAS MORÉ OLIVARES
nβ1 + β2∑Xi = ∑Yi
β1∑Xi + β2∑Xi2 = ∑XiYi
En general, para un modelo con K variables explicativas el producto X’X es:
X’X =
n
∑X2i
∑X3i
...
∑Xki
∑X2i
∑X22i
∑X2iX3i
...
∑X2iXki
∑X2iXki
∑X3iXki
.
.
.
∑Xki
∑X2ki
∑Yi
∑X2iYi
∑X3iYi
∑XkiYi
X’Y =
Si tenemos una ecuación de regresión:
Yi =
βi + β2X2i + β3X3i +... βkXki + e
La suma de cuadrados de los residuos
n
SCR =
n
∑ [y - β1 - β2X2i - β3X3i -... βkXki]2 es mínima.
i=i
La ecuación Yi =
múltiple.
β1 + β2X2i + β3X3i +... βkXki representa la recta de regresión
En econometría se realizan dos tipos de juicios: estimación de parámetros y
contrastación de hipótesis.
El objetivo del económetrista, es que la estimación se aproxime lo más posible al verdadero valor del parámetro que se pretende estimar y por ello, el
estimador cumple con tres propiedades: insesgadez, óptimo, eficiencia. Un
estimador es insesgado si su esperanza coincide con el valor del parámetro
que pretende aproximar; el estimador lineal e insesgado de menor varianza
será el óptimo y se conoce como MELI 2 , un estimador será eficiente cuando
tenga la menor varianza posible.
2 ELIO.
Economía y Desarrollo - marzo 2005, vol. 4, n° 1
43
ESBOZOS DE ECONOMETRÍA FINANCIERA
En una muestra obtenida una estimación de βi mediante expresiones mínimo cuadráticas se puede verificar o contrastar hipótesis acerca del valor del
parámetro. Así, se quiere verificar que β1 toma un valor concreto h, planteamos como hipótesis nula Ho: β1 = h y como hipótesis alternativa H1 = β1 ≠ h.
βi - βi
Dado que
————
Sβi
≈ tn-2, bajo hipótesis nula se puede obtener un valor
βi - h
empírico t*, t* = ————
Sβi
≈ tn-2. Este valor se contrastará con el valor teórico
registrado en las tablas a un nivel de significación del p por ciento y n-2
grados de libertad (test de dos colas). Si el valor del estadístico obtenido es tal
que |t*| > tP/2 se rechazará la Ho y en caso contrario se acepta (véase figura 3 ).
Acepta Ho
Rechaza Ho
-tP/2
Rechaza Ho
X
-tP/2
Pero en economía no suele ser habitual que una sola variable afecte a la
variable de interés, sino que existe mayor complejidad, o sea, existen influencias múltiples sobre la variable de interés.
Así, un modelo lineal múltiple se puede expresar de la siguiente manera:
Yi =
βi + β2 X2i + β3X3i +... + βkXki + Ui
donde Yi es la variable explicada, cuyo comportamiento viene influido por un
conjunto de variables explicativas, X2, X3,... Xk, y por un término de perturbación aleatorio Ui.
3
También existe test de una sola cola.
Universidad Autónoma de Colombia
44
ELÍAS MORÉ OLIVARES
3. Riesgo y su medición
El riesgo se puede considerar como la posibilidad de que el rendimiento real
proveniente de poseer un valor se desvíe del rendimiento esperado. Además
de considerar su rango, el riesgo de un activo se puede medir cuantitativamente utilizando estadísticas como el coeficiente de variación y la desviación estándar.
La distribución de probabilidades se puede resumir en términos de dos variables: el valor esperado del rendimiento y la desviación estándar (GITMAN,
2003).
n
El valor esperado de rendimiento es R = ∑Ri Pi donde
Ri = Rendimiento para la posibilidadi
Pi = Probabilidad que ocurra ese rendimiento.
n = Número total de posibilidades.
La desviación estándar es
δ=
∑(Ri – R)2Pi
En la realidad los inversionistas seleccionan las acciones acorde con el principio de elevar al máximo la utilidad esperada en términos de esas dos variables. Así:
E (U) = f(R,δ)
Un inversionista racional trata de maximizar su rentabilidad y minimizar
el riesgo asociado, cuando debe repartir una suma de dinero entre diferentes opciones de inversión. El problema de la selección de portafolio surge
porque la rentabilidad de las acciones depende de factores ajenos al control
del inversionista o decisor. Por lógica el inversionista configurará con varias acciones que no se comporten de manera similar para compensar las
pérdidas con ganancias, o sea, sigue el refrán popular de “no poner todos los
huevos en una misma canasta” (CAICEDO, 1997).
En el portafolio de inversiones se puede distinguir el riesgo sistemático y el
no sistemático. El primero es un riesgo no diversificable y es el riesgo del
mercado asociado a los cambios en la economía por factores internos o externos, modificaciones en las políticas de países asociados, guerras. El riesgo no sistemático se debe a factores propios o internos de la firma, es propio
a esa compañía e independiente de factores económicos, políticos o sociales, asociándole factores como huelgas, cambios tecnológicos, competencia
(GITMAN, 2003).
Economía y Desarrollo - marzo 2005, vol. 4, n° 1
45
ESBOZOS DE ECONOMETRÍA FINANCIERA
4. Selección de portafolio
A la teoría sobre selección de portafolio contribuyeron varios pioneros como
el premio nóbel HARRY MARKOWITZ, FAMA, MILLER, TOBIN y sobre el modelo CAPM,
SHARPE, LINTNER y FAMA (BODIE y MERTON, 2003).
Markowitz propuso en 1952 la regla del “valor esperado-varianza” o regla E-V
(por expected value-variance). Según la regla un decisor preferirá un proyecto A sobre un proyecto B si alguna de las siguientes afirmaciones es
válida:
i)
La rentabilidad esperada de A es mayor o igual a la de B y la varianza de
A es menor que la de B.
ii)
La rentabilidad esperada de A es mayor que la de B y la varianza de A es
menor o igual a la de B.
La combinación de todas las posibilidades de las acciones producía un conjunto de oportunidades, que al limitarlas estableciendo las condiciones anotadas, adoptaba una frontera (VAN HORNE, 2000).
Esto significa que el decisor escogerá una combinación o portafolio sobre la
frontera eficiente: no hay ningún portafolio con mayor rentabilidad, dado un
nivel de riesgo, ni ninguno que presente menor nivel de riesgo dado un
nivel de rentabilidad. El nuevo problema es determinar cuál será el punto
en esa línea que el decisor debe escoger.
En el modelo CAPM (Capital Asset Pricing Model ó MVAC) se demostró que ese
punto óptimo m, era el portafolio de todas las acciones del mercado ponderadas por el valor total transado de cada una y cualquier decisor escogería
siempre ese portafolio 4 .
La recta que une el punto de la rentabilidad de cero riesgo y el portafolio
óptimo m, se llama línea de mercado de capitales (LMC) y es la nueva frontera
eficiente.
Así, la rentabilidad de un portafolio se puede calcular con la
ecuación Rp = pR + (1 – p) Rm.
5. Comentarios sobre el
MVAC
LMC
mediante la
y modelos alternos
Sobre la validez del modelo de valuación de activos de capital (MVAC=CAPM) han
surgido serias preguntas.
4
TOBIN. Teorema de separación. 1958.
Universidad Autónoma de Colombia
46
ELÍAS MORÉ OLIVARES
En general el modelo de valuación de activos de capital se basa en datos
históricos y en ese caso las betas no siempre reflejan la variabilidad futura
de los rendimientos, de manera que los rendimientos requeridos especificados
en el modelo se consideran aproximaciones sin mucha precisión.
Además el MVAC está basado en un supuesto mercado eficiente con muchos inversionistas pequeños, igualmente informados, sin restricciones en
las inversiones, con inversionistas racionales, que prefieren rendimientos
más altos y riesgo más bajo. Un estudio (FAMA y FRENCH, 1992) ha mostrado
que no existe una relación significativa entre betas históricas y rendimientos históricos entre más de 2.000 acciones, de 1963 a 1990. Expresado de
otra manera significa que la magnitud de la beta histórica de una acción no
estaba relacionada con el nivel de su rendimiento histórico.
Existe una teoría más amplia, denominada teoría de valuación por arbitraje
(VPA ó APT), desarrollada en los setenta y que ha recibido mucha atención en
la literatura financiera. Esta teoría sugiere que la prima por riesgo de valores se podría explicar mejor mediante varios factores fundamentales y no el
rendimiento de mercado que usa en el MVAC, de manera que el MVAC se puede
considerar como un derivado del APT. Además que la teoría del APT confirma la
importancia del rendimiento del mercado, no ha podido identificar con claridad otros factores de riesgo (ROSS, 1976).
Sin embargo, el MVAC no se ha abandonado del todo porque su “defecto histórico” no desacredita su validez como modelo de expectativas, de manera que
aún es útil para vincular el riesgo esperado no diversificable y el rendimiento. Por último, las fallas en los modelos FAMA-ROSS y la falta de aceptación
y uso práctico APT, conserva válido el MVAC.
6. Ejercicio aplicado
La línea de mercado de capital (LMC) de la teoría del portafolio postula una
relación lineal entre el retorno o rendimiento esperado y el riesgo (medido
por la desviación estándar) para portafolios eficientes, así: Ei = β1 + β2 σi,
donde Ei = rendimiento esperado del portafolio i y σ1 = desviación estándar de
rendimiento. Se cuenta con la siguiente información sobre el rendimiento
esperado y la desviación estándar del mismo para los portafolios de 34 fondos
mutuos de inversión en los Estados Unidos para el período 1963 - 1997. Verifiqué hasta qué punto las cifras respaldan la teoría. (Véase tabla 1) (GUJARATI,
1990).
Economía y Desarrollo - marzo 2005, vol. 4, n° 1
47
ESBOZOS DE ECONOMETRÍA FINANCIERA
Determinar si la desviación estándar influye sobre el retorno esperado (prueba de significancia).
(x’x) β = x’y
-1
n ∑X
β1
∑Y
β1
=
;
β2
∑X∑X2
∑XY
9380
34
546,1
466,8
546,1
9380,43
7754,66
=
β2
- 546,1
MC (X’X) =
9380,43
- 546,1
- 546,1
34
; Adj (X’X) =
- 546,1
34
Adj(X’X)
————— = (X’X)-1
D
= (349380,43) – (546,1)2
= 318934,62 - 298225,21
= 20709,41
Det
Det
9380,43
------------20709,41
- 546,1
------------20709,41
- 546,1
------------20709,41
34
-----------20709,41
(x’x)-1 =
β1
0,4529
; (x’x)-1 =
0,4529
- 0,0264
- 0,0264
466,8
=
β2
-0,0264
β1
0,0016
•
7754,66
;
6,6907
β1 = 6,6907
0,4220
β2 = 0,4220
Universidad Autónoma de Colombia
0,0016
(0,4529 – 466,8) + (-0,0264 . 7754,66)
;
(-0,0264 . 466,8) + (0,0016 . 7754,66)
=
β2
- 0,0264
48
ELÍAS MORÉ OLIVARES
Tabla 1
Comportamiento de 34 fondos mutuos de inversión, 1963 - 1997
Rendimiento anual
promedio %
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
A11
A12
A13
A14
A15
A16
A17
A18
A19
A20
A21
A22
A23
A24
A25
A26
A27
A28
A29
A30
A31
A32
A33
A34
15.6000
9.0000
10.5000
11.0000
12.9000
13.4000
14.8000
15.7000
11.9000
14.3000
14.3000
11.5000
14.2000
14.6000
16.0000
15.5000
16.5000
14.1000
11.4000
14.5000
16.4000
12.3000
11.0000
16.5000
18.6000
18.3000
18.5000
11.4000
11.1000
10.7000
11.3000
13.9000
11.3000
13.8000
Desviación estándar
del rendimiento anual
promedio %
14.0000
8.2000
12.5000
15.3000
14.6000
11.1000
15.8000
18.3000
12.7000
20.4000
14.9000
10.9000
18.2000
17.7000
22.5000
22.0000
20.7000
18.1000
13.1000
24.5000
20.8000
11.5000
9.4000
19.8000
21.7000
18.9000
16.8000
9.2000
15.0000
12.3000
18.4000
19.9000
11.0000
15.9000
Desempeño de 34 fondos mutuos 1963 - 1997
Economía y Desarrollo - marzo 2005, vol. 4, n° 1
Universidad Autónoma de Colombia
Desempeño de 34 Fondos Mutuos 1963 - 1997
FONDOS
16,06176471
13,72941176
14,0000
8,2000
12,5000
15,3000
14,6000
11,1000
15,8000
18,3000
12,7000
20,4000
14,9000
10,9000
18,2000
17,7000
22,5000
22,0000
20,7000
18,1000
13,1000
24,5000
20,8000
11,5000
9,4000
19,8000
21,7000
18,9000
16,8000
9,2000
15,0000
12,3000
18,4000
19,9000
11,0000
15,9000
546,1000
218,4000
73,8000
131,2500
168,3000
188,3400
148,7400
233,8400
287,3100
151,1300
291,7200
213,0700
125,3500
258,4400
258,4200
360,0000
341,0000
341,5500
255,2100
149,3400
355,2500
341,1200
141,4500
103,4000
326,7000
403,6200
345,8700
310,8000
104,8800
166,5000
131,6100
207,9200
276,6100
124,3000
219,4200
7.754,6600
X²
Y²
196,0000
67,2400
156,2500
234,0900
213,1600
123,2100
249,6400
334,8900
161,2900
416,1600
222,0100
118,8100
331,2400
313,2900
506,2500
484,0000
428,4900
327,6100
171,6100
600,2500
432,6400
132,2500
88,3600
392,0400
470,8900
357,2100
282,2400
84,6400
225,0000
151,2900
338,5600
396,0100
121,0000
252,8100
9.380,4300
243,3600
81,0000
110,2500
121,0000
166,4100
179,5600
219,0400
246,4900
141,6100
204,4900
204,4900
132,2500
201,6400
213,1600
256,0000
240,2500
272,2500
198,8100
129,9600
210,2500
268,9600
151,2900
121,0000
272,2500
345,9600
334,8900
342,2500
129,9600
123,2100
114,4900
127,6900
193,2100
127,6900
190,4400
6.615,5600
x
-2,0618
-7,8618
-3,5618
-0,7618
-1,4618
-4,9618
-0,2618
2,2382
-3,3618
4,3382
-1,1618
-5,1618
2,1382
1,6382
6,4382
5,9382
4,6382
2,0382
-2,9618
8,4382
4,7382
-4,5618
-6,6618
3,7382
5,6382
2,8382
0,7382
-6,8618
-1,0618
-3,7618
2,3382
3,8382
-5,0618
-0,1618
-
y
1,8706
-4,7294
-3,2294
-2,7294
-0,8294
-0,3294
1,0706
1,9706
-1,8294
0,5706
0,5706
-2,2294
0,4706
0,8706
2,2706
1,7706
2,7706
0,3706
-2,3294
0,7706
2,6706
-1,4294
-2,7294
2,7706
4,8706
4,5706
4,7706
-2,3294
-2,6294
-3,0294
-2,4294
0,1706
-2,4294
0,0706
-
xy
-3,8567
37,1815
11,5024
2,0792
1,2124
1,6345
-0,2802
4,4106
6,1501
2,4753
-0,6629
11,5077
1,0062
1,4262
14,6186
10,5142
12,8506
0,7553
6,8992
6,5024
12,6539
6,5206
18,1827
10,3571
27,4615
12,9724
3,5218
15,9839
2,7918
11,3959
-5,6805
0,6548
12,2971
-0,0114
257,0282
x²
4,2509
61,8073
12,6862
0,5803
2,1368
24,6191
0,0685
5,0097
11,3015
18,8203
1,3497
26,6438
4,5721
2,6838
41,4509
35,2626
21,5132
4,1544
8,7721
71,2038
22,4509
20,8097
44,3791
13,9744
31,7897
8,0556
0,5450
47,0838
1,1273
14,1509
5,4673
14,7321
25,6215
0,0262
609,1005
y²
3,4991
22,3673
10,4291
7,4497
0,6879
0,1085
1,1462
3,8832
3,3467
0,3256
0,3256
4,9703
0,2215
0,7579
5,1556
3,1350
7,6762
0,1373
5,4262
0,5938
7,1320
2,0432
7,4497
7,6762
23,7226
20,8903
22,7585
5,4262
6,9138
9,1773
5,9020
0,0291
5,9020
0,0050
206,6706
49
Media de X
Media de Y
15,6000
9,0000
10,5000
11,0000
12,9000
13,4000
14,8000
15,7000
11,9000
14,3000
14,3000
11,5000
14,2000
14,6000
16,0000
15,5000
16,5000
14,1000
11,4000
14,5000
16,4000
12,3000
11,0000
16,5000
18,6000
18,3000
18,5000
11,4000
11,1000
10,7000
11,3000
13,9000
11,3000
13,8000
466,8000
XY
ESBOZOS DE ECONOMETRÍA FINANCIERA
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
A11
A12
A13
A14
A15
A16
A17
A18
A19
A20
A21
A22
A23
A24
A25
A26
A27
A28
A29
A30
A31
A32
A33
A34
RENDIMIENTO
DESVIACIÓN
ANUAL
ESTÁNDAR DEL
PROMEDIO
RENDIMIENTO
% "Y"
ANUAL % "X"
50
ELÍAS MORÉ OLIVARES
Podemos sintetizar el modelo econométrico mediante la ecuación:
Y = 6,6907 + 0,4220 X
E = 6,6907 + 0,4220 σ
•
Cálculo del error estándar
∑e2
σ2 = ———;
n-2
(∑xy)2
∑e2 = ∑y2 - ——————
∑X2
∑e2 = 206,6706 – (257,0282)2 / 609,1003
∑e2 = 98,2098
σ
2
=
98,2098
—————;
34 – 2
σ
2
98,2098
= ————— ;
32
σ2 = 3,0690
σ2
3,0690
Var(β 2) = ------- ; Var(β2) = --------------- ;
∑x2
609,1003
EEe (β2) =
Var (β2)
; EEe (β2) =
Var(β2) = 0,0050
0,0050
; EEe (β2) = 0,0071
Prueba de Significancia con Estadístico Tc
Al no tener una hipótesis nula, basada en la experiencia se calculará una
prueba de regresión tomando como hipótesis nula que: β2 = 0.
Ho:
β2 = β2* = 0
H1:
β2 = β2* ≠ 0
β2 - β2*
0,4220 - 0
tc = ————— = ——————
σβ2
0,071
tc = 5,9437
Economía y Desarrollo - marzo 2005, vol. 4, n° 1
51
ESBOZOS DE ECONOMETRÍA FINANCIERA
Con un nivel de confianza del 95% tα/2 será:
Grados de libertad:
α = 0,05
n–2
gl = 34 – 2
gl = 32
t 32f; 0,025 = 2,042
0,025
0,025
Z
A
- 2,042
2,042
tc, cae en la zona de rechazo, por tanto, no se acepta la hipótesis nula.
•
Para saber los intervalos del coeficiente de regresión tenemos:
β2 = 0,4220; EE (β2) = 0,071; α 5%; t.32; 0,025 = 2,042
[β2 - tα/2 σβ2 ≤ β2 ≤ β2 + tα/2 σβ2] = 1 - α
P
P [0,4220 – 2,042
P [0,277018
• 0,071 ≤ β2 ≤ 0,4220 + 2,042 • 0,071] = 95%
≤ β2 ≤ 0,566982] = 0,95
La interpretación de este intervalo de confianza es que dado un coeficiente
de confianza del 95% en el largo plazo, en 95 de cada 100 casos intervalos
como (0,277018; 0566982) contendrán el verdadero β2 porque este intervalo
es ahora fijo, dejando de ser aleatorio; en consecuencia, β2 está o no está en
el intervalo: la probabilidad de que el intervalo fijo que se especifique contenga el verdadero valor de β2 es uno (1) o cero (0).
2.
Establecer la bondad del ajuste (R2).
∑e2
2
R = 1 - ————;
∑y2
98,2098
R2 = 1 - ——————;
206,6706
Universidad Autónoma de Colombia
R2 = 0,5248
52
3.
•
ELÍAS MORÉ OLIVARES
Efectuar prueba de análisis de varianza (F)
Suponemos que las perturbaciones Ui se distribuyen normalmente; y si
Ho: β2 = 0 con 1 y n – 2
F1, n-2 gl,
Ho: β2 = 0
H1: β2 ≠ 0
∑e2 = 98,2098;
∑y2 = β22 ∑ X2;
gl = n – 2, gl = 32
∑y2 = 12012,9
gl = n – 1, gl = 33
gl = 1
∑y2 = (0,4220)2 (609,1003)
∑e2/gl =
98,2098
————— ;
32
∑e2/gl = 3,0690 ;
∑y2 = 108,4710
108,4710
∑y2 = ——————
1
∑y2 = 108,4710
108,4710
Fc = ———————
3,0690
Fc = 35,3434
F1, n-2 gl = F0,05; 1,32 gl = 4,17
Z.A
4,17
Fc, cae en la zona de rechazo, por tanto se rechaza la hipótesis nula.
Los cambios en X explican el 52,48% de los cambios en Y.
Economía y Desarrollo - marzo 2005, vol. 4, n° 1
ESBOZOS DE ECONOMETRÍA FINANCIERA
53
7. Comentarios sobre el modelo
Se rechaza la hipótesis nula utilizando la “Regla de decisión” que expresa:
Construye un intervalo de confianza del 100 (1-α) por ciento para β Si el valor
de β bajo Ho cae dentro de este intervalo de confianza, acepta Ho, pero si cae
fuera del intervalo rechace Ho.
Por último r2 mide la bondad global del ajuste del modelo de regresión estimado si es razonablemente alto, sin olvidar que ese r 2 se puede aumentar
agregando al modelo variables explicativas adicionales. Se puede decir que
los resultados son buenos porque los signos de los coeficientes estimados
están acorde con las expectativas teóricas. Así, la línea de mercados de capital ( LMC ) de la teoría del portafolio tiene pendiente positiva, o sea, que los
resultados son consistentes con la teoría. Ver ecuación Y = 6,6907 + 0,4220X.
Esta ecuación acorde con la teoría refleja el rendimiento requerido en el
mercado para cada nivel de riesgo diversificable (beta).
En resumen un r2 de 52.48% es estadísticamente significativo y explica la
teoría y no debe exagerarse la importancia del criterio de un valor de r 2
cercano al 80% ó 90%.
8. Conclusiones
A pesar que existen paquetes econométricos como el RATS , el ejercicio de
econometría financiera realizado es interesante porque muestra la validez
del MVAC para vincular el riesgo esperado no diversificable y el rendimiento.
Además permite mostrar a la comunidad académica, especialmente a los
estudiantes de ciencias administrativas y contables el uso y combinación
de la econometría con las finanzas para cuantificar y tomar decisiones generales con mayor precisión.
Resumiendo, a pesar de las críticas del modelo de valuación de activos de
capital recientemente planteadas ( MVAC ), éste se mantiene vigente. Se demostró utilizando un modelo de regresión lineal en que los coeficientes de
la línea de mercados de capitales (LMC) coinciden con la teoría. Se necesita
evaluar los estudios que tratan de demeritar el MVAC. En realidad las cifras
respaldan la teoría.
Bibliografía
BODIE, Z. y MERTON, R. (2003). Finanzas. México. Prentice may, 1ª ed.
CAICEDO, E. (1997). Modernas teorías financieras. Mercados emergentes y determinantes de
la inversión en la nación. Serie de Pliegos Administrativos y Financieros. Univalle.
Universidad Autónoma de Colombia
54
ELÍAS MORÉ OLIVARES
FAMA, E. y FRENCH K. (1992). “The Cross-Section of Expected Stock Returns”, Journal
of Finance, june.
GITMAN, L. (2003). Fundamentos de administración. Harla.
GREEN, W. (1998). Econometría, 3ª ed., Prentice Hall.
GUJARATI, D. (1990). Econometría, McGraw-Hill.
MARTÍN, G.; LABEAGA, J.M. y MOCHON, F. (1997). Introducción a la econometría. Prentice Hall.
ROSS, S. (1976). “The Arbitrage Theory of Capital Asset Pricing”. Journal of Finance.
VAN HORNE, J. (2000). Administración financiera, 7ª ed., Prentice Hall.
Volver al Contenido
Economía y Desarrollo - marzo 2005, vol. 4, n° 1