Consigna 1 (VOLUMEN): Consigna 2 (VOLUMEN):

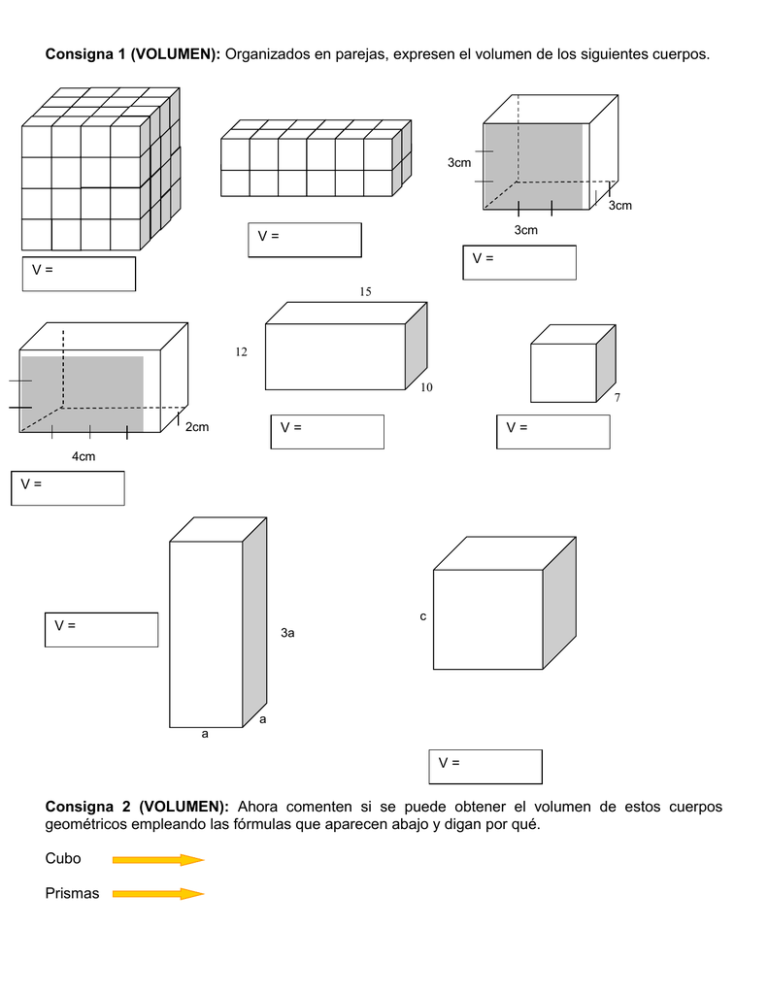
Consigna 1 (VOLUMEN): Organizados en parejas, expresen el volumen de los siguientes cuerpos.
3cm
3cm
3cm
V=
V=
V=
15
12
10
2cm
7
V=
V=
4cm
V=
c
V=
3a
a
a
V=
Consigna 2 (VOLUMEN): Ahora comenten si se puede obtener el volumen de estos cuerpos
geométricos empleando las fórmulas que aparecen abajo y digan por qué.
Cubo
Prismas
V= ABh
(Área de la base x altura)
Consigna 3 (VOLUMEN): Organizados en equipos de tres compañeros armen los desarrollos planos
de los prismas que se encuentran abajo. Cuiden dejar una cara del prisma cuadrangular sin pegar.
Consigna 4 (VOLUMEN): Una vez armados los cuerpos, calculen su volumen. Expliquen su
procedimiento.
Consigna 5 (VOLUMEN): Organizados en equipos de tres alumnos, realicen las siguientes
actividades.
a) Recorten el desarrollo plano de la pirámide que está enseguida y peguen sus caras cuidando
dejar la base sin pegar.
b) Comparen la pirámide que acaban de armar y el prisma cuadrangular que armaron antes y
señalen semejanzas y diferencias.
c) Llenen la pirámide con sal y vacíen el contenido en el prisma cuadrangular anterior, háganlo
tantas veces como sea necesario para llenar el prisma. Al terminar de hacer esto contesten
las siguientes preguntas.
◊ ¿Cuántas veces vaciaron el contenido completo de la pirámide en el prisma?
◊ ¿Qué relación habrá entre lo que hicieron y la fórmula para calcular el volumen de una
pirámide (V = ABh o V = 1/3 ABh )?
Consigna 6 (VOLUMEN): En equipos, resuelvan el siguiente problema:
Un tanque de almacenamiento de agua instalado en una comunidad tiene forma de prisma
rectangular y una capacidad de 8 000 litros, su base mide 2.5 m por 2 m. Si lo necesitas consulta la
siguiente tabla de equivalencias.
m3 (metro cúbico)
dm3 (decímetro cúbico)
cm3 (centímetro cúbico)
1 m3
= 1000 dm3 = 1000 l (litros)
1 m3
= 1000 000 cm3
1 dm3
= 1000 cm3 = 1 l
1 dm3
= 1000 000 mm3
1 cm3
= 1 000 mm3
a) ¿Qué altura tiene este tanque?
b) ¿Qué cantidad de agua contendría si sólo llegara el agua a una altura de 75 cm?
c) Si el tanque tuviese la misma capacidad (8 000 l), pero fuese de forma cúbica, ¿cuales serían
sus dimensiones?
Consigna 7 (volumen): Organizados en equipos, contesten las siguientes preguntas:
En un envase con forma de prisma cuadrangular cuya base mide 5 cm por lado caben 250 cm3 de
aceite.
a) ¿Cuál es la altura de la caja?
b) ¿Cabría la misma cantidad de aceite en un envase forma de pirámide cuya base y altura sean
iguales que en el envase anterior? Justifica tu respuesta.
c) ¿Qué condiciones deben cumplirse para que un envase con forma de prisma y otro con forma
de pirámide que tienen la misma base, tengan la misma capacidad? ¿Por qué?
Consigna 8 (volumen): En equipos, completen la tabla siguiente. Pueden usar calculadora.
Cuerpo
Prisma cuadrangular
Prisma cuadrangular
Prisma cuadrangular
Prisma cuadrangular
Prisma rectangular
Prisma rectangular
Prisma rectangular
Prisma rectangular
Datos de la base
Largo (cm)
Ancho (cm)
Altura del cuerpo
(cm)
Volumen
(cm3)
10
360
360
240
240
160
160
180
180
3
4
9.6
8
5
5
2
2
3
10
20
Consigna 9 (volumen): Organizados en los mismos equipos, hagan una tabla como la anterior y
con las mismas dimensiones de la base y altura de los prismas, calculen el volumen de las
pirámides. Pueden usar calculadora.
Cuerpo
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide rectangular
Pirámide rectangular
Pirámide rectangular
Pirámide rectangular
Datos de la base
Largo (cm)
Ancho (cm)
Altura del cuerpo
(cm)
Volumen
(cm3)
10
3
4
9.6
8
5
5
2
2
3
10
20
Consigna 10 (volumen): Ahora, si el volumen de las pirámides fuese el mismo que el de los
prismas, ¿cuáles deberían ser las dimensiones? Pueden usar calculadora.
Cuerpo
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide cuadrangular
Pirámide rectangular
Pirámide rectangular
Pirámide rectangular
Pirámide rectangular
Datos de la base
Largo (cm)
Ancho (cm)
Altura del cuerpo
(cm)
Volumen
(cm3)
10
360
360
240
240
160
160
180
180
3
4
9.6
8
5
5
2
2
3
10
20