Matematicas Grado 11 Leticia
Anuncio

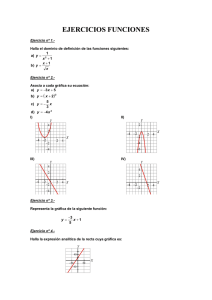
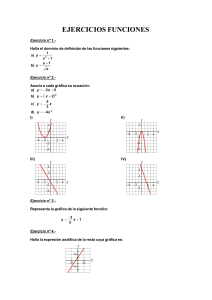
Institución Educativa Dinamarca Plan de Apoyo 2015 Área: Matemáticas Período: II Grado: 11 A-B Docente: Leticia Lopera Zuleta Nombre del estudiante: ________________________________________________________________________________ Etapa No 1 2 Actividad Plan de acción Fecha de entrega Forma de entrega Lugar de entrega Actividades escritas acerca de toda la temática trabajada durante el periodo. (Valor del 30%). 2 de julio de 2015 En trabajo escrito, con normas INCONTEC IE Dinamarca – Aula 204 Sustentación escrita, por medio de evaluación tipo PRUEBA SABER (Valor 70%) 8 de julio de 2015 Escrita, en clases IE Dinamarca – Aula 204 ACTIVIDAD ESCRITA CÁLCULO Actividad uno: Inecuaciones Cuadráticas, Racionales y con Valor Absoluto Resolver las siguientes inecuaciones 1. 2x2 – 3x – 36 > x2 +2x 2. 3x2 + 16x – 12 < 0 3. 4x(x + 3) -5 4. 3(2x2 + 1) > 11x 5. 5x2 + 4x – 1 0 6. x2 x 20 2x 1 x 2 7. 2x x 5 0 x 12 x 2 ( x 12)(x 2) 8. x 1 x 2 x 3 x 1 2x 1 x 1 9. x 1 2 x2 10. Resolver el siguiente enunciado problema: El peso promedio que un atleta básico levanta es de 150,2 𝐾𝑔 y el 95% de estos atletas levanta un peso 𝑚 que cumple la desigualdad 𝑚 − 150,2 | |≤2 5,8 Al resolver esta desigualdad se determina el intervalo en el que oscilan las pesos levantados por estos atletas. Hallar dicho intervalo, explicando la respuesta. Actividad dos: Funciones (Básicas) 1. Halla el dominio de definición de las funciones siguientes (Justifican como lo halla en cada caso): a) y b) y 1 x 1 2 x 1 x 2. Representa la gráfica de la siguiente función: y x 2 4 3. Con 200 metros de valla queremos acotar un recinto rectangular aprovechando una pared: a) Llama x a uno de los lados de la valla. ¿Cuánto valen los otros dos lados? b) Construye la función que nos da el área del recinto (Muestra tu razonamiento). 4. El perímetro de un rectángulo es de 30 cm. Obtén la función que nos dé el área del rectángulo en función de la longitud de la base (Muestra tu razonamiento). 5. El precio por establecimiento de llamada en cierta tarifa telefónica es de 0,12 euros. Si hablamos durante 5 minutos, la llamada nos cuesta 0,87 euros en total. Halla la función que nos da el precio total de la llamada según los minutos que estemos hablando (Muestra tu razonamiento). 6. En algunos países se utiliza un sistema de medición de la temperatura distinto a los grados centígrados que son los grados Farenheit. Sabiendo que 10°C = 50°F y que 60°C =140°F, obtén la ecuación que nos permita traducir temperaturas de °C a °F (Muestra tu razonamiento). 7. Una compañía de transporte público recogió en una gráfica la información que tiene sobre la venta de bonos para viajar en sus líneas. a) ¿Durante cuánto tiempo se hizo este estudio? b) ¿En qué momento del año 1999 se vendieron menos bonos? ¿Y en cada uno de los años 2000 y 2001? c) ¿En qué momento del año 2001 se produce la máxima venta? ¿A qué lo atribuyes? d) ¿En qué periodos anuales es mayor el crecimiento en la venta de bonos? ¿En qué estación del año es decreciente la venta? 8. Describe el comportamiento de un carrusel mediante la siguiente gráfica, que relaciona el tiempo que transcurre desde que comienza a moverse hasta que empieza una nueva vuelta a) ¿Es una función periódica?............. b) ¿Cuál es el periodo?.................. c) Desde que comienza a moverse ¿Durante cuánto tiempo aumenta su velocidad?......................................... d) ¿Cuánto tiempo mantiene la velocidad constante?.......................................... e) ¿Cuánto tiempo está parado?.................. 9. En cada una de estas gráficas indica: Dominio, Recorrido, Intervalos de crecimiento y decrecimiento, los máximos y los mínimos. Indica también si alguna es discontinua o si alguna es periódica. (Organiza estos datos en una tabla) 10. Los coches, una vez se compran, empiezan a perder valor a un ritmo de un 10% anual, aproximadamente. a) Haz una tabla de valores que nos dé el valor de un coche que costó 20000 €, en años sucesivos. b) Representa la función años- valor del coche. c) Halla una fórmula que permita calcular el precio del coche en función de los años transcurridos hasta su venta.