tema 8 : aplicación de las derivadas
Anuncio
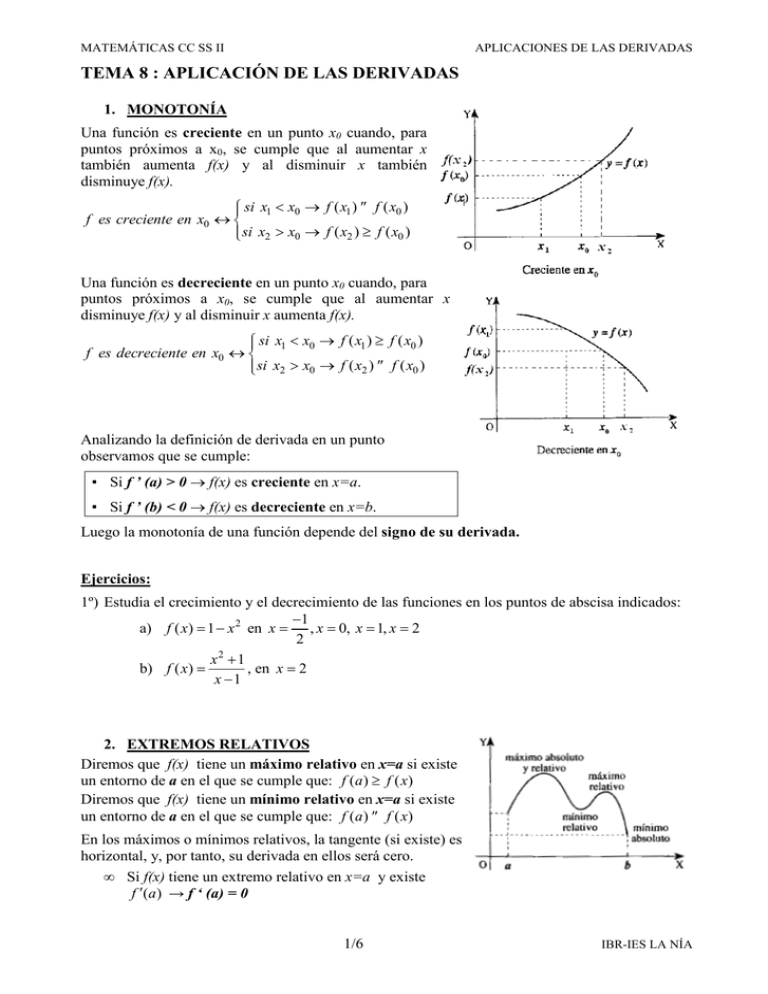
MATEMÁTICAS CC SS II APLICACIONES DE LAS DERIVADAS TEMA 8 : APLICACIÓN DE LAS DERIVADAS 1. MONOTONÍA Una función es creciente en un punto x0 cuando, para puntos próximos a x0, se cumple que al aumentar x también aumenta f(x) y al disminuir x también disminuye f(x). si x1 < x0 → f ( x1 ) ≤ f ( x0 ) f es creciente en x0 ↔ si x2 > x0 → f ( x2 ) ≥ f ( x0 ) Una función es decreciente en un punto x0 cuando, para puntos próximos a x0, se cumple que al aumentar x disminuye f(x) y al disminuir x aumenta f(x). si x1 < x0 → f ( x1 ) ≥ f ( x0 ) f es decreciente en x0 ↔ si x2 > x0 → f ( x2 ) ≤ f ( x0 ) Analizando la definición de derivada en un punto observamos que se cumple: ▪ Si f ’ (a) > 0 → f(x) es creciente en x=a. ▪ Si f ’ (b) < 0 → f(x) es decreciente en x=b. Luego la monotonía de una función depende del signo de su derivada. Ejercicios: 1º) Estudia el crecimiento y el decrecimiento de las funciones en los puntos de abscisa indicados: −1 a) f ( x) = 1 − x 2 en x = , x = 0, x = 1, x = 2 2 2 x +1 b) f ( x) = , en x = 2 x −1 2. EXTREMOS RELATIVOS Diremos que f(x) tiene un máximo relativo en x=a si existe un entorno de a en el que se cumple que: f (a ) ≥ f ( x) Diremos que f(x) tiene un mínimo relativo en x=a si existe un entorno de a en el que se cumple que: f (a ) ≤ f ( x) En los máximos o mínimos relativos, la tangente (si existe) es horizontal, y, por tanto, su derivada en ellos será cero. • Si f(x) tiene un extremo relativo en x=a y existe f ′(a ) → f ‘ (a) = 0 1/6 IBR-IES LA NÍA MATEMÁTICAS CC SS II APLICACIONES DE LAS DERIVADAS Ejercicios: 2º) Estudia los intervalos de monotonía y los extremos relativos de las funciones. a) f ( x) = x 2 − 3 b) f ( x) = x3 − 3 x 2 − 9 x + 1 x c) f ( x) = 2 x +1 x −1 d) f ( x) = 2x +1 e) f ( x) = x3 − 3x 2 + 3x + 6 3º) Se calcula que entre las 2000 y 5000 revoluciones por minuto el consumo de gasolina de un motor viene dado por la función f(x)=2x2-12x+23, donde f(x) indica los litros consumidos en una hora y “x” viene expresada en miles de revoluciones por minuto. Averigua los tramos en que a mayor nº de revoluciones por minuto corresponde más consumo de gasolina. Halla las revoluciones con las que el consumo del motor es máximo y con las que es mínimo y dichos consumos. (Sep-02) 4º) Al vender un producto a un precio x entre 40 y 65 €, el beneficio es y = x2+100x2100. Obtén razonadamente el precio que maximiza el beneficio. ¿Qué ocurre si el precio está entre 55 y 70? 5º) Se considera la siguiente función x2 + 2x + 1 x < −1 a) Estudia su continuidad y derivabilidad. f ( x) = 2 x + 2 −1 ≤ x ≤ 2 b) Representa gráficamente la función y, a la vista su 2 x>2 gráfica, determina sus máximos y mínimos relativos, así − x + 8 x como el crecimiento y decrecimiento. 6º) Sea la función Estudia su continuidad y derivabilidad. Estudia el 1 5 crecimiento e investiga si hay asíntotas x < −2 x + 2 f ( x) = − x −2 ≤ x < 1 x2 − 3 x ≥1 x ≤ −2 x+a 2 7º) Dada la función: . f ( x) = x − 2a − 2 < x ≤ 2 a) Halla el valor de “a” para que f sea continua en todos los números reales. (a=2) b) Representa la función f y estudia su derivabilidad. [Pico en x=-2] 4x − 8 x>2 8º) La calificación f(x) obtenida por un estudiante en cierto examen depende de las horas de preparación a través de la función: x a) Estudia el conjunto de valores positivos de x 5 para los que f(x) es creciente. ¿Tiene sentido f ( x ) = 2x afirmar que a más tiempo de preparación corresponde más calificación? 0'2 x + 3 b) ¿Hay algún punto en que estudiar un poco más puede ser muy rentable? c) ¿Se puede obtener la calificación 10? Justifica la respuesta. 0 ≤ x ≤ 15 15 < x 9º) Dada la función: a) Halla el valor de a para que la función y= f(x) sea continua en el intervalo [0,8]. x+2 b) Halla los máximos y mínimos absolutos de y= f(x) 2 en el intervalo [0,4]. Justifica que los puntos f ( x ) = x − 6 x + 12 encontrados son máximos y mínimos absolutos. − 2x + a c) Calcula el área de la región del plano limitada por las rectas de ecuación y=0 , x=0 , x=3 y la gráfica de y=f(x). 2/6 0≤x<2 2≤x≤4 4< x≤8 IBR-IES LA NÍA MATEMÁTICAS CC SS II APLICACIONES DE LAS DERIVADAS 3. SEGUNDA DERIVADA. CONCAVIDAD E INFLEXIÓN. Una función es cóncava hacia arriba, ∪, en un punto xo si en las proximidades de xo la gráfica de la función queda por encima de la recta tangente en xo. Una función es cóncava hacia abajo, ∩, en un punto xo si en las proximidades de xo la gráfica de la función queda por debajo de la recta tangente en xo. Una función tiene un punto de inflexión en xo si en las proximidades de xo la gráfica de la función cambia de posición respecto de la recta tangente en xo. (la tangente atraviesa a la gráfica de la función). En los puntos de inflexión la gráfica de la función pasa de ser cóncava a convexa, o al revés. El estudio de la concavidad se realiza con la segunda derivada: • Si f “ (a) > 0 → f(x) es cóncava hacia arriba en x=a • Si f “ (b) < 0 → f(x) es cóncava hacia abajo en x=b • Si f(x) tiene un punto de inflexión en x=c → f ”(c)=0 Criterio de la 2º derivada para la Clasificación de Extremos Relativos: ▪ Si f’(a)=0 y f “(a)>0 → f(x) tiene un mínimo relativo en x=a. (ya que es ∪) ▪ Si f’(b)=0 y f “(b)<0 → f(x) tiene un máximo relativo en x=b. (ya que es ∩) Ejercicios: 10º) Determina los extremos relativos, la concavidad y los puntos de inflexión de las funciones: a) f ( x) = x3 − 6 x 2 − 15 x + 40 b) f ( x) = x 4 x+2 c) f ( x) = x −3 6x d) f ( x) = 1 + x2 11º) El beneficio diario obtenido por una empresa, en función del nº x de unidades producidas, 1 viene dado por la función f ( x) = x 3 − 4 x 2 + 12 x . Dibuja la gráfica de dicha función para 3 0 ≤ x ≤ 8 , deduciendo para qué valores se obtienen los beneficios máximos y mínimos. 3/6 IBR-IES LA NÍA MATEMÁTICAS CC SS II APLICACIONES DE LAS DERIVADAS 4. REPRESENTACIÓN GRÁFICA DE FUNCIONES Realizaremos un estudio que comprenda los siguientes puntos: 1) Dominio 2) Continuidad 3) Asíntotas. Además de las asíntotas verticales y horizontales que ya conocemos, calcularemos un tercer tipo de asíntotas: asíntotas oblicuas. ▪ Verticales: x=a, siempre que lim f ( x) = ∞ x →a ▪ Horizontales: y=b, siendo b = lim f ( x) x →∞ ▪ Oblicuas: y=mx+n, siendo m = lim x →∞ f ( x) y n = lim ( f ( x) − mx) x →∞ x 4) Puntos de corte con los ejes 5) Monotonía 6) Extremos relativos 7) Concavidad – Puntos de inflexión. (Este último punto no será necesario si ya sabemos dibujar la gráfica de la función) Ejercicios: 12º) Representación gráfica de las siguientes funciones: 1) f ( x) = x2 +1 , x2 −1 6) f ( x) = 2) x f ( x) = , 1+ x2 7) x2 − 2x + 2 , f (x) = x −1 3) f ( x) = 1 , 1+ x2 8) f (x) = 4) f ( x) = x 3 − 3x 2 + 2 x , 9) 5) f ( x) = 4 x 4 − 5 x 2 + 1 , f ( x) = 3 , x − 3x 3 x2 − 2x − 8 x 2x 1− x2 13º) La función f(x) = x3 + ax2 +bx + c pasa por el punto (-1,0) y tiene un máximo en el punto (0,4). Halla los coeficientes de f(x) su mínimo y su punto de inflexión. [f(x)=x3-3x2+4, I(1,2)] 14º) Calcula a y b para que la función f(x)=x3+ax2+bx+1 tenga un mínimo en el punto (2,-15). [a=0, b=-12] 15º) Se ha comprobado empíricamente que las ganancias que proporciona cierto juego dependen del 100 x tiempo que se esté jugando a través de la expresión: G ( x) = 2 , donde x representa el tiempo x + 400 de juego expresado en minutos. Se pide: a) ¿Cuánto más tiempo se permanezca jugando es mayor la ganancia obtenida? Justifica la respuesta. b) Determina el tiempo de juego que proporciona la mayor ganancia.[20 min] c) ¿Puede ocurrir que si se sobrepasa cierto tiempo, el juego dé pérdidas? ¿Por qué? 4/6 IBR-IES LA NÍA MATEMÁTICAS CC SS II APLICACIONES DE LAS DERIVADAS 16º) El índice de inflación de cierto país fue variando, durante el año 2007, según la expresión: t 2 − 8t , donde t es el tiempo en meses desde principios del año. Se pide: i (t ) = 15 + 20 a. ¿Durante qué meses el índice de inflación fue creciendo? b. ¿A partir de qué mes se supera la inflación inicial del mes de enero? c. Si el gobierno tiene previsto devaluar la moneda cuando el índice de inflación alcance 16,5, ¿en qué mes tomará la decisión? 17º) La cuenta de resultados (pérdidas o ganancias) en millones de euros, y, de una empresa vienen 5 x 2 + 20 x − 25 dadas por la siguiente función de los años de existencia x de la misma: f ( x) = x2 + 7 a) ¿A partir de qué año deja la empresa de tener pérdidas? b) ¿En qué momento alcanza la empresa sus ganancias máximas? ¿A cuánto ascienden éstas? c) Describe la evolución de la cuenta de resultados de la empresa. ¿Cuáles serán sus beneficios a muy largo plazo? (Sep-08) 18º) Nos dicen que la función f(t)=t-2 es la derivada de la inflación en función del tiempo en cierto país, cuando 0 ≤ t ≤ 5 . Determina el valor de t para el que la inflación alcanza el valor mínimo. 19º) Los beneficios anuales, B(x), en miles de euros, previstos por una empresa para los próximos años vienen dados por la siguiente función, donde x representa el número de años a partir del actual: 25 x B( x) = 2 x + 16 a) ¿En algún momento se alcanzará un beneficio de 2500 €? [Si, 2 y 8 años] b) ¿Puede esta empresa tener pérdidas algún año? ¿Por qué? (Jun06) [No, porque B(x) ≥ 0 ] c) ¿Cuántos años han de transcurrir para que la empresa obtenga el máximo beneficio? Justifica que es máximo. [4 años, beneficio de 3125€] 20º) Se sabe que el número de individuos de una determinada población de una especie protegida vendrá dado, durante los próximos años, por la función: n(t ) = 15000t + 10000 , siendo “t” el número 2t + 2 de años transcurridos. Se pide: a) El tamaño actual de la población b) ¿Cómo evoluciona el tamaño de la población entre los años 4 y 9?.¿Cuántos años deben pasar hasta que haya 7.250 individuos? c) Si esta función fuese válida indefinidamente, ¿se estabilizaría el tamaño de la población? d) Razona si el número de individuos está aumentando o disminuyendo y hasta dónde podría llegar. 5. OPTIMIZACIÓN: Un problema de optimización es aquel en el que es necesario determinar el valor que hace que una función, de la que no tenemos su expresión analítica, sea máxima o mínima, sometida a ciertas condiciones. Debemos determinar: 1. Las variables que intervienen ,normalmente una o dos (es más frecuente que sean dos). 2. La expresión analítica de la función que se desea optimizar (obtener el máximo o el mínimo). 3. Mediante los datos del problema, obtener alguna condición (ecuación) que permita expresar la función utilizando una sola variable. Esto sólo es necesario cuando interviene más de una variable. 4. Obtener el máximo o el mínimo de dicha función. 5/6 IBR-IES LA NÍA MATEMÁTICAS CC SS II APLICACIONES DE LAS DERIVADAS Ejercicios: 21º) Descompón 18 como suma de dos números positivos, de manera que el producto de uno de ellos por el cuadrado del otro sea máximo. 22º) Disponemos de 400 m de tela metálica para cercar un rectángulo de terreno. ¿Cuánto deben medir los lados del rectángulo para que el área encerrada en la cerca sea la máxima posible? 23º) Entre todos los rectángulos de perímetro 12 cm, ¿cuál tiene la diagonal menor? ¿Cuánto mide ésta? [3cm, 3cm, d= 3 2 cm] 24º) Recortando un cuadradito de cada esquina de unos cartones rectangulares de dimensiones 6 y 8 cm, se pueden construir cajas sin tapa. ¿Qué medida deben tener estos cuadraditos para que el volumen de las cajas sea máximo? [1'13cm] 25º) Un pastor dispone de 1000 m de tela metálica para construir una cerca rectangular aprovechando una pared ya existente. Halla las dimensiones de la cerca para que el área encerrada sea máxima. [250/500] 26º) Calcula la longitud que deben tener los lados de un terreno rectangular de 400 m2 de área si queremos que el gasto en la cerca sea el mínimo posible. [100x100] 27º) Una página rectangular ha de contener 300 cm2 de letra impresa. Los márgenes superior e inferior de la página son de 2,5 cm y los laterales tienen 2 cm. ¿Cuáles han de ser las dimensiones de la página de modo que la cantidad de papel empleada sea mínima? [19’5 y 24’84] 28º) Disponemos de 2.880 € para vallar un campo rectangular, uno de cuyos lados da al camino. La valla de ese lado cuesta 8 € el metro y la de los otros lados 1€ el metro. ¿Cuál es el área máxima que podremos vallar con ese dinero? 29º) El coste de un marco para una ventana rectangular es de 14 € por cada metro de alto, y 10 € por metro de ancho. Si queremos que la ventana tenga 2m2 de superficie, ¿cuáles deben ser las dimensiones del marco para que resulte lo más económico posible? 30º) Nos disponemos a cercar un terreno rectangular. Al vallar el terreno lo vamos a dividir en tres parcelas rectangulares iguales mediante dos vallas divisorias paralelas a los lados más pequeños del rectángulo. Si tenemos 8000 m de valla ¿qué dimensiones del terreno maximizan el área vallada? 31º) Un agricultor tiene la cosecha sin recolectar. Actualmente hay 6.000 kg de patatas y se las pagan a 10 céntimos el kilo. Cada semana la cosecha aumenta en 500 kg más, pero el precio baja medio céntimo el kilo. ¿Cuándo debe recolectar la cosecha para que su ganancia sea máxima? ¿Cuánto ganará? [4 semanas] 32º) En unos almacenes se tienen 2.000 kg de alimentos perecederos que se pueden vender a 3€ el kg, pero si se venden más tarde, el precio aumenta en 0’1€ el kg cada día. Calcula cuándo interesa vender estos alimentos para tener los máximos ingresos si cada día que pasa se estropean 50 kg de ellos. ¿Cuáles son estos ingresos máximos? ¿Cuántos los kilos que se venden y a qué precio? Justifica que es máximo. (Sep05) [6125€; 1750kg; 3’50€/kg] 6/6 IBR-IES LA NÍA






