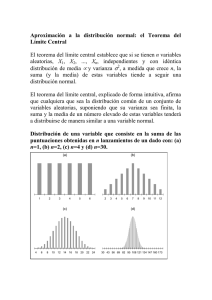
para descargar el archivo

Cátedra I Estadística II
Autor I Hebe Goldenhersch
INFERENCIA ESTADÍSTICA: TEORÍA DE LA ESTIMACIÓN
I
Objetivos
Este Capítulo tiene por propósitos centrales:
Comprender el concepto de estimador y estimación puntual;
Conocer las propiedades de los buenos estimadores y por lo menos un
método para obtenerlos;
Comprender el concepto de estimación por intervalos, así como los de
errores de estimación, nivel de confianza;
Determinar el tamaño necesario de una muestra en distintas situaciones;
Calcular e interpretar intervalos de confianza para algunos parámetros y
diferencias o cocientes de parámetros.
Contenidos
1.
2.
3.
4.
5.
6.
7.
8.
9.
Introducción.
Estimación puntual.
Propiedades de los buenos estimadores.
El método de "Máxima Verosimilitud". Aplicaciones.
Estimación por intervalos. Definición de "Intervalos de Confianza".
5.1. Desarrollo de un ejemplo.
5.2. Planteo general de la estimación por intervalos.
Intervalos de confianza para la media, para la proporción, para la varianza.
6.1. Varianza poblacional conocida.
6.2. Varianza poblacional desconocida. Población normal.
6.3. Intervalos de confianza para la proporción poblacional.
6.4. Intervalos de confianza para la varianza en poblaciones normales.
Determinación del tamaño de muestra para la media, para la proporción.
7.1. Muestreo con reemplazo, o en poblaciones infinitas. Estimación de la
media o de la proporción.
7.2. Error, riesgo y tamaño de la muestra.
7.3. Determinación del tamaño de la muestra teniendo en cuenta el error
relativo.
Determinación del tamaño de muestra para poblaciones finitas.
Intervalos de confianza para la diferencia de medias, de proporciones y
cociente de varianzas.
9.1. Diferencia de medias, muestras independientes.
9.2. Varianzas poblacionales conocidas.
9.3. Varianzas poblacionales desconocidas.
9.4. Diferencia de medias, muestras dependientes (observaciones apareadas).
9.5. Diferencia de proporciones. Muestras independientes.
9.6. Intervalo de confianza para el cociente de varianzas. Poblaciones normales.
9.7. Consideraciones generales para interpretar los intervalos de confianza para diferencias de medias o proporciones y cocientes de varianzas.
7
Cátedra I Estadística II
Autor I Hebe Goldenhersch
8
Cátedra I Estadística II
Autor I Hebe Goldenhersch
1. Introducción
Iniciamos aquí el tratamiento de un tema fundamental de la disciplina, que resume
una manera de “razonar” y permite entender la utilidad de la estadística en los más
variados campos de conocimiento. Nos referimos a la Inferencia Estadística, que se
aplica básicamente con dos objetivos alternativos:
Estimación de parámetros
INFERENCIA ESTADÍSTICA
Contraste de hipótesis
Nos referimos a la estimación de parámetros (recordar o repasar en los materiales
de Estadística I qué es un parámetro de una población) cuando desconocemos los
parámetros de una población y para aproximarnos al conocimiento de esos valores
desconocidos tomamos una muestra de la población y a partir de ella “estimamos” el o
los parámetros (si se trata de una variable cuantitativa, se puede estimar por ejemplo
la media, la varianza; si se trata de una variable dicotómica se puede estimar la
proporción de “éxitos”, etc.).
El contraste de hipótesis también se realiza a partir de una muestra tomada de la
población de interés, pero en ese caso se trata de poner a prueba (o contrastar)
alguna hipótesis referida ya sea al valor de un parámetro o a las características de la
población (si tiene cierta forma su distribución, si hay o no independencia entre dos
variables, entre otros).
Recomendamos leer los ejemplos planteados en las páginas 3 y 4, y pensar en cuáles
de ellos se aplicarían métodos de estimación de parámetros y en cuáles pruebas de
hipótesis1/.
Con estos ejemplos disponibles, avanzaremos ahora en el análisis más pormenorizado
de la cuestión.
2. Estimación puntual
En la vida cotidiana, es habitual hablar de “estimación”: “estimo que hoy lloverá”,
“estimo que no vendrán”, “estimo que el promedio de este alumno es cercano a
seis”...
Sin embargo, cuando buscamos precisión estadística, se presentan algunas dificultades.
El problema de la "estimación" de parámetros surge porque en muchos casos, la
población que desea estudiarse es, o muy grande, o infinita, o resulta difícil acceder a
su conocimiento total por diversos motivos (vinculados al costo o no).
Entonces se recurre al muestreo. Naturalmente, cuando se desea conocer el valor de
algún parámetro de una población, por ejemplo la media, la varianza, la proporción y
resulta inviable el estudio de toda la población, surge la idea de "estimar" el valor de
ese o esos parámetros.
1/
Respuesta: los casos 1, 3 y 5 corresponden a prueba de hipótesis, los números 2, 4 y 6 a
estimación de parámetros. El último puede ser planteado ya sea como estimación o como
prueba de hipótesis, según cómo se formule el problema.
9
Cátedra I Estadística II
Autor I Hebe Goldenhersch
¿Y cómo puede estimarse el valor de un parámetro? Es necesario poseer alguna
información sobre la población ya que sería imposible intentar alguna estimación de un
parámetro poblacional sin información alguna de la población de que se trata.
Entonces se toma una muestra de esa población, se calculan "estimadores" o
"estadísticos" a partir de la muestra, que servirán para proporcionar una idea de los
valores posibles de esos parámetros poblacionales desconocidos.
Existen distintos tipos de muestreo, que se analizarán más adelante; pero todos ellos
deben garantizar, para que se pueda aplicar la teoría estadística y extender las
conclusiones de la muestra hacia la población, que cada observación de la población
tenga una probabilidad conocida de ser elegida en la muestra.
Es natural pensar que si se quiere conocer algo sobre la media poblacional ( µ ), se
acuda a estimadores como la media muestral ( X ), o la mediana de la muestra, o el
promedio entre el menor y el mayor valor de la muestra, etc.
¿Cuál de ellos resultará un mejor estimador de
µ?
Para poder elegir un estimador,
existen algunos criterios que fijan ciertas propiedades deseables para los estimadores.
Y así será utilizado el estimador de un parámetro que cumpla con todas o la mayoría
de esas propiedades. Existen también ciertos métodos de estimación que proporcionan
los mejores estimadores cuando se conocen algunas características de la población.
Antes de dar algunas definiciones importantes para comprender el tema que estamos
tratando, nos pondremos de acuerdo sobre alguna simbología. Simbolizaremos en
general con letras griegas a los parámetros, y con letras latinas a los estimadores o
estadísticos (los parámetros corresponden a la población, los estimadores o
estadísticos a la muestra); simbolizaremos la media poblacional con µ (la letra griega
mu), y la media muestral con X ; la varianza poblacional con
σ2
(sigma al cuadrado)
2
y la varianza muestral con s ; la proporción poblacional (siempre que hablamos de
una población dicotómica nos referimos a la proporción de “éxitos”) con P o p
(algunos textos la simbolizan con π ), y la proporción muestral (proporción de “éxitos”
en la muestra) con p̂ (p “con sombrero” o simplemente “p sombrero”). Simbolizaremos con θ (la letra griega Theta) un parámetro cualquiera de la población, y con θˆ
(Theta con sombrero...) el estimador de ese parámetro. En general, salvo que
indiquemos lo contrario, se utilizarán indistintamente las mayúsculas o minúsculas.
Precisemos ahora la definición de estimador
Cuando se toma una muestra de n observaciones a partir de una población determinada, se llama estimador
ciones muestrales.
θˆ
de un parámetro
θ,
a cualquier función de las observa-
Recordemos que cada observación muestral es una variable aleatoria, por lo tanto un
estimador de un parámetro por ser función de variables aleatorias, es una variable
aleatoria.
A cada valor particular de un estimador, es decir al valor que asume para una muestra
determinada, se lo llama estimación. Así, la media muestral
media poblacional µ :
µˆ = X
Cuando se toma una muestra, y se calcula su media:
10
X
es un estimador de la
Cátedra I Estadística II
Autor I Hebe Goldenhersch
x=
x es
una estimación particular de
1
[ x1 + x2 + ... + xn ]
n
µ
(observar que hemos simbolizado con minúscula
la estimación, valor particular, y con mayúscula el estimador, variable aleatoria). Si
recordamos que un estimador puede asumir cualquier valor dentro del rango posible
determinado por su distribución de probabilidad, advertimos que la concreción de una
estimación puntual no permite realizar afirmaciones ciertas ni probabilísticas acerca del
verdadero valor del parámetro, o de la confianza que puede depositarse en el
estimador. Este último objetivo se logra mediante la estimación por intervalos, que
trataremos más adelante; pero la estimación por intervalos siempre toma como punto
de partida estimadores puntuales que cumplan con propiedades deseables.
Con la definición que dimos de estimador, como “cualquier función de las observaciones muestrales”, parecería obvio que pueden resultar tantos estimadores como
funciones uno pueda imaginar. En realidad no ocurre así, porque antes de elegir un
estimador, se presta atención a sus propiedades. Hay estimadores que cumplen ciertas
propiedades que otorgan confianza en que cada estimación particular que se realice
utilizándolo proporcionará un resultado no muy alejado del parámetro.
A continuación hablaremos sobre las propiedades deseables de los estimadores, o
propiedades de los buenos estimadores.
3. Propiedades de los buenos estimadores
Comenzamos ejemplificando con un juego, que nos proporcionará una idea acerca
de qué queremos decir con esto de “buenos estimadores”.
Supongamos que se realiza un concurso de tiro al blanco, y el curso de Estadística
II quiere seleccionar un estudiante que lo representará. En la prueba final, cada
tirador deberá tirar un solo tiro, y el que pegue más cerca del blanco será el
ganador.
En el curso se presentan cuatro postulantes para intervenir, y para probarlos, cada
uno tira seis veces al blanco, con los siguientes resultados:
•
•
•
•••
••
•
•
•
• ••
• •
•
•
•
•
•
Juan
•
•
•
Adriana
Pablo
Martín
Si a cualquier persona se le pregunta a quién elegiría como representante en el
campeonato, contestará que a Pablo. ¿Por qué? Vemos que si bien Pablo no siempre
acierta, “en promedio” sus tiros dan en el blanco, y además la dispersión no es muy
grande. Adriana presenta un “promedio” igual al de Pablo, pero tienen mucha
dispersión... entonces, es razonable decir que es ”más probable que Pablo en lugar de
Adriana acierte en el blanco”. Juan, por su parte, presenta poca dispersión, pero “en
promedio” sus tiros pegan lejos del blanco. Y Martín... bueno, ni en promedio se
acerca, y además su dispersión es muy grande.
Si pensamos en cada estudiante (cada tirador) como un “estimador” y cada tiro como
una “estimación”, y en el blanco como el “parámetro” que se desea alcanzar,
11
Cátedra I Estadística II
Autor I Hebe Goldenhersch
inmediatamente definiremos estas propiedades que nos permitirán decir que elegimos
a Pablo porque es “insesgado y eficiente”. Como suplente, ¿Adriana o Juan? Para
decidir, diremos en principio que Adriana es “insesgada” pero “ineficiente”, y Juan
“eficiente pero sesgado”. Piense una respuesta imaginando quién de los dos tiene más
chance de corregir su problema... Confronte luego sus ideas con algunas pistas en el
pie de página2/.
Definimos ahora las propiedades deseables de los estimadores, conceptos que
aclararán la ejemplificación anterior.
a) Insesgabilidad
Se dice que un estimador es insesgado, cuando su valor esperado es igual al
parámetro que se estima:
E ( θˆ ) = θ
Ya se explicó que los estimadores o estadísticos son variables aleatorias; para cada
una de las muestras posibles pueden asumir valores diferentes, y cada valor o
intervalo de valores posibles tiene asociada una probabilidad. Un estimador tiene,
entonces, una distribución de probabilidad (recordar de Estadística I el caso de la
media muestral o la proporción muestral) y por lo tanto puede calcularse su
esperanza. El hecho que la esperanza del estimador sea igual al parámetro a estimar,
por supuesto no asegura ni aproximadamente que de una estimación a realizar surgirá
un resultado igual al parámetro, sólo se trata de una propiedad teórica, que afirma que
si se toman todas las muestras posibles, el promedio de los valores del estimador o
sea su valor esperado será igual al parámetro. En cada realización, el valor del
estimador puede resultar más o menos alejado de ese valor esperado. ¿De qué
depende que no resulte muy alejado? Depende de la variabilidad del estimador, es
decir de la desviación estándar (o el error estándar)3/ del estimador. En efecto,
siempre que el valor esperado no esté muy lejos del parámetro, será preferible entre
dos estimadores posibles aquél que tenga menor variabilidad, puesto que en este caso
las probabilidades de que en cada muestra el estimador esté cercano al parámetro
serán mayores.
Si existiera un diferencia entre la esperanza del estimador o estimador y el parámetro
a estimar, esa diferencia se denomina "sesgo ".
Sesgo = E ( θˆ )- θ
2/
3/
Si es posible conocer el sesgo (Juan tiene algún problema con la vista o con su arma) se lo
puede corregir (hacer un pozo en el suelo, por ejemplo, para que pegue más abajo...); en
cambio la eficiencia (variabilidad) no se puede corregir fácilmente. Elegiríamos a Juan,
enseñándole a corregir el sesgo.
Existe acuerdo en llamar “error estándar” a la “desviación estándar” de un estimador. Por eso
se dice, por ejemplo, el error estándar de la media muestral es igual a la desviación estándar
poblacional dividida por la raíz cuadrada de n.
12
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Veamos algunos ejemplos:
Son estimadores insesgados: para la media poblacional
(se estudió en Estadística I que E(
proporción muestral
p̂ ;
X
µ , la media muestral X
µ ); para la proporción poblacional (p) la
)=
cuando se consideran dos poblaciones y se estiman sus
parámetros tomando una muestra en cada una, son estimadores insesgados de la
diferencia de medias poblacionales, la diferencia de medias muestrales; de la
diferencia de proporciones poblacionales, la diferencia de proporciones muestrales,
etc.
Es sesgado, en cambio, el estimador de la varianza poblacional calculado mediante
la varianza muestral con la fórmula:
S sc2 =
∑( xi − x ) 2
n
ya que resulta:
E( S sc )= σ
2
2
n −1
n
(1)
Por esto se sugirió utilizar como estimador de la varianza poblacional, la varianza
muestral corregida:
∑( xi − x ) 2
S =
n −1
2
Usted puede comprobar que de esta manera se corrige el "sesgo" (aplicar propiedades
de la esperanza sabiendo que la varianza muestral corregida es igual a la varianza sin
corregir multiplicada por n/(n-1), sabiendo de (1) cuál es la esperanza de esta última).
En el ejemplo del tiro al blanco, serían “estimadores insesgados” Adriana y Pablo.
Hay estimadores sesgados, pero "asintóticamente insesgados" (este es el caso de la
varianza muestral no corregida), ya que significa que si bien presentan un sesgo, al
aumentar el tamaño de la muestra, el sesgo tiende a desaparecer. En la fórmula (1) se
advierte que si n es suficientemente grande, la esperanza del estimador es
prácticamente igual al parámetro.
b) Consistencia
Se dice que un estimador
θˆ
es consistente si:
lim
n→ ∞
( Pr
θˆ − θ < ∈
)= 1
Esto significa que un estimador es consistente cuando al tomar muestras grandes (a
eso nos referimos con n “tiende” a infinito), es seguro que el estimador se aproximará
al parámetro. Dicho de otra manera, hay una probabilidad igual a 1 de que la
diferencia (“error” lo llamaremos más adelante) entre el estimador y el parámetro será
inferior a un número arbitrario ∈ (pequeño).
Si recuerdan de Estadística I la Ley de los Grandes Números, ésta proporciona una
evidencia de la consistencia de los estimadores media y proporción muestral (¿por
qué?)
13
Cátedra I Estadística II
Autor I Hebe Goldenhersch
¿Le parece razonable pensar que son consistentes aquellos estimadores cuyas
varianzas (o sus errores estándar) tienden a cero al crecer el tamaño muestral?
Puede verificarse (aunque aquí no lo haremos), que la varianza muestral también es
un estimador consistente de la varianza poblacional.
La mediana muestral, que como estimador de la media poblacional es insesgado si la
distribución poblacional es simétrica, no es un estimador consistente de la media,
aunque sí de la mediana poblacional. ¿Qué significa esto? Que al tomar muestras
grandes, la media de la muestra se aproximará a la media poblacional, pero la
mediana de la muestra se aproximará a la mediana de la población (estimador
consistente de la mediana poblacional) y no a la media.
La consistencia es una propiedad deseable y muy importante de los estimadores
cuando se usan muestras grandes. Si éstas son pequeñas no tiene relevancia el hecho
de que un estimador sea o no consistente.
c) Eficiencia
Esta propiedad es muy importante, porque se refiere precisamente a la variabilidad de
los estimadores a la cual se hizo referencia al hablar de insesgamiento. La varianza de
un estimador, proporciona una idea del grado de confianza que se puede tener en el
mismo.
Ante dos estimadores insesgados (o por lo menos consistentes) θˆ1 y θˆ2 es más eficiente
θˆ1 si:
V( θˆ1 ) < V( θˆ2 )
Generalmente la comparación se hace realizando el cociente entre ambas varianzas; si
es menor que 1, el estimador del numerador es más eficiente que el del denominador
y viceversa.
Es claro que cuanto menor sea la varianza de un estimador, es más probable que
asuma valores cercanos al parámetro (siempre que sea insesgado) y por lo tanto, será
un mejor estimador.
En el ejemplo del tiro al blanco, Juan y Pablo tienen menor varianza que el resto, pero
Juan es sesgado; es muy probable que pegue cerca... pero no del blanco, sino de “su
valor esperado” que no es igual al parámetro. Para estas situaciones, es conveniente
introducir el concepto de “eficiencia en error cuadrático medio”. Si uno de los
estimadores es sesgado y el otro insesgado, pero el primero tiene menor variabilidad
que el segundo, suele ser conveniente elegirlo a pesar del sesgo (por eso elegíamos a
Juan antes que Adriana)4/.
El concepto de eficiencia a que nos referimos aquí, es el de “eficiencia relativa” porque
se compara la eficiencia de dos estimadores. Un ejemplo interesante es que surge de
comparar la media y la mediana muestrales como estimadores de la media poblacional. Sabemos que la varianza de la media muestral es:
4/
[
La varianza de un estimador es E (θˆ − E (θˆ )
[
coincide con E (θˆ − θ )
2
2
].
Si el estimador es insesgado, esta fórmula
] ; pero si es sesgado, la última fórmula no es la varianza sino el “error
cuadrático medio” del estimador, y mide su dispersión con respecto al verdadero valor del
parámetro. Si un estimador es sesgado, pero su ECM es pequeño, será preferible a uno
insesgado pero con ECM (o varianza) mayor.
14
Cátedra I Estadística II
Autor I Hebe Goldenhersch
V (X ) =
σ
2
n
En cambio la varianza de la mediana muestral es:
V(med) = 1.25332
σ
2
(Esto es
n
Resulta así que V ( X ) < V ( med ) ;
π
multiplicado por la varianza de la media muestral)
2
ó
V (X )
< 1
V ( m ed )
Esto significa que, siendo ambos estimadores insesgados de la media poblacional, por
tener la media muestral un menor error estándar, habrá mayor probabilidad de que la
media muestral se encuentre cerca de la media poblacional que la mediana.
Es útil reiterar en este punto que se habla de probabilidades. Esto es que, en un caso
particular, puede ocurrir un suceso que tenga baja probabilidad (alguna vez usted
puede ganar la grande...), y entonces tal vez en una realización particular, la mediana
muestral resulte más cercana a la media poblacional que la media muestral, pero ello
no es muy probable.
Existe otro concepto de eficiencia, se trata de la eficiencia absoluta. Este es conocido
como la “acotación de Rao- Cramer”, y permite establecer, dada una distribución
poblacional, cuál es la varianza mínima de un estimador de cada parámetro. Este tema
no será tratado en esta asignatura.
d) Suficiencia
Un estimador es suficiente cuando utiliza toda la información que surge de la muestra
con respecto al parámetro a estimar. Esta es una definición intuitiva, la definición
rigurosa va más allá de los objetivos de este curso, y se puede consultar en la
bibliografía5/.
Con un ejemplo, se comprenderá cuándo un estimador no es suficiente. Si en una
población se desea estimar la media poblacional, se toma una muestra de tamaño n y
se define como estimador de la media, la siguiente función de las observaciones
muestrales:
µˆ =
x1 + x2
2
Es decir, el promedio de las dos primeras observaciones. Puede comprobarse que este
estimador es insesgado, pero no utiliza la información proporcionada por las n-2
observaciones restantes; por ello decimos que no es un estimador suficiente.
Algunos autores mencionan otras propiedades (que el lector interesado puede
consultar en la bibliografía), tales como “estimadores asintóticamente normales”,
refiriéndose a aquellos estimadores cuya distribución es normal al crecer el tamaño
muestral -tal como ocurre con todos los casos donde se aplica el Teorema Central del
Límite- o “estimadores robustos”
aquéllos que no se ven muy afectados ante
pequeños desvíos respecto del cumplimiento de ciertos supuestos6/.
Proponemos ahora varias Actividades sobre estos temas.
5/
6/
Canavos, G.: Probabilidad y Estadística - McGraw Hill (1995) - pág. 261.
Peña, Daniel: "Fundamentos de Estadística". Ciencias Sociales, Alianza Editorial Madrid 2001,
Canavos (op. cit).
15
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Actividad 1:
Se considera que el tiempo de duración promedio de cierta batería se distribuye
con media µ y varianza 1. Tomamos una muestra aleatoria de tamaño 2, y como
deseamos realizar una estimación puntual de la duración promedio poblacional, se
nos sugieren 3 estimadores:
µ$1 =
µ$ 2 =
µ$ 3 =
1/3 x1 + 2/3 x2
1/4 x1 + 3/4 x2
1/2 x1 + 1/2 x2
donde x1 y x2 componen la muestra de tamaño 2.
Se pide:
a) ¿Son insesgados estos estimadores?
b) ¿Cuál de ellos permitirá realizar estimaciones más precisas? ¿Porqué?
Actividad 2:
Sea x1, x2 y x3 valores de ingreso familiar de una muestra de tamaño 3,
tomada del total de familias de una ciudad con media µ y varianza σ2.
Considerando los siguientes estimadores del promedio del ingreso familiar,
¿cuál de ellos elegiría y porqué?
µ$1 = 1/3 x1
µ$ 2 = 1/9 x1
µ$ 3 = 4/10 x1
+ 1/3 x2 + 1/3 x3
+ 3/9 x2 + 5/9 x3
+ 2/10 x2 + 4/10 x3
Actividad 3:
Una muestra de los diámetros de 5 pelotas de tenis anotados por un vendedor
fueron:
6,33 cm.
6,37 cm.
6,36 cm.
6,32 cm.
6,37 cm.
Suponga que los diámetros se distribuyen en forma normal:
a) Calcular una estimación con un estimador insesgado y eficiente:
1) de la media poblacional
2) de la varianza poblacional
b) Determinar un estimador insesgado pero ineficiente del diámetro
promedio poblacional.
c) Determinar un estimador insuficiente de la media poblacional.
Este método se basa en el hecho, intuitivamente comprensible, que distintos párametros poblacionales producirán muestras diferentes. Así, por ejemplo si se tiene una
población en la que se estudia el peso de las personas, si la media poblacional es de
70 kg., seguramente los valores observados en una muestra extraída de esa población, serán diferentes a los que resulten de una muestra extraída de una población
donde la media es de 55 kg.
El método de Máxima verosimilitud, consiste en seleccionar como valor estimado del
parámetro, aquél que maximiza la probabilidad de una muestra (a posteriori de
haberla extraído) con respecto a todos los valores posibles del parámetro.
16
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Se trata de un método muy utilizado para obtener estimadores, porque se comprueba
que los estimadores máximo verosímiles gozan de la mayoría de las propiedades
enunciadas en el punto anterior (a veces son sesgados, pero el resto de las propiedades siempre está presente); esto significa que haber encontrado un estimador máximo verosímil es haber encontrado un “buen” estimador del parámetro desconocido.
Un ejemplo7/, ayudará a entender este concepto, no muy simple para la intuición.
Se tomó una muestra con reposición de diez profesores en una Facultad, y se
encontró que tres se manifiestan favorables a constituir un sindicato. Con este
resultado muestral, ¿cuál sería la estimación de la proporción de profesores sobre
el total de la Facultad, que desean constituir el sindicato?
Esa proporción puede ser (mencionando sólo algunos de todos los posibles valores
entre 0 y 1): 0, 0,1, 0,2,... 0,9, ó 1?
Por la distribución binomial, puede calcularse cuál es la probabilidad de obtener
tres respuestas favorables en una muestra de tamaño 10, para los distintos
valores posibles de p (observe que a diferencia de los problemas que resolvió en
Estadística I con la distribución binomial, donde se calculaba la probabilidad de
cierto número de éxitos conociendo p y n, aquí se trata de encontrar la
probabilidad de obtener x éxitos, donde x ya es conocido porque ya se tomó la
muestra - 3 en este caso particular- para distintos valores de p).
P
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
P(x=3,10,p)
0.0000
0.0574
0.2013
0.2668
0.2150
0.1172
0.0425
0.0090
0.0008
0.0000
0.0000
Evidentemente no se elegiría p = 0 ó p = 1 como estimador de p en la población,
porque en la muestra hubo 3 que contestaron afirmativamente, entonces p no
puede ser igual a cero, y hay 7 que contestan negativamente, luego p no puede
ser igual a 1.
Del resto de valores posibles de p, se advierte que 0.3 es el que proporciona la
mayor probabilidad que en una muestra de 10 ocurran 3 opiniones favorables,
luego 0.3 es el estimador máximo verosímil o de máxima probabilidad de p.
En general, es posible obtener estimadores máximo verosímiles en forma analítica a
partir de la función de probabilidad conjunta de una muestra. En Estadística I se
explicó el concepto de distribución conjunta de probabilidad de n observaciones
muestrales. Es claro que esa distribución depende de la forma de la distribución
poblacional, de las observaciones muestrales y del o los parámetros poblacionales.
El caso de la distribución normal. Para la distribución normal, con media µ y
varianza
σ2,
la distribución conjunta de las observaciones muestrales, llamada
función de verosimilitud, que depende de las observaciones muestrales y del o los
parámetro desconocidos es: (ver Estadística I, Capítulo VII).
7/
La parte numérica es del libro Análisis Estadístico de Ya Lun Chou - Interamericana - México
1985 (pág. 218).
17
Cátedra I Estadística II
Autor I Hebe Goldenhersch
n
n
 1  − 12 ∑
 e i =1
L( µ , σ ) = f ( X1 , X2 ,..., X n ; µ , σ ) = 
2
 2πσ 
2
( xi − µ )2
σ2
2
(2)
Esta función se plantea una vez que se obtuvo la muestra, y por lo tanto las
conocidas, tiene como incógnitas a
µ
σ
y
2
X i son
. Si se busca el máximo de L( µ , σ 2 ) con
respecto a ambos parámetros, se obtienen los valores de µ y σ que otorgan la
2
máxima probabilidad a la muestra. Esos valores son los estimadores “máximo
verosímiles” o de “máxima probabilidad” para los parámetros.
Para encontrar este máximo se sugiere tomar logaritmo natural de L, porque siendo el
logaritmo una función monótona (tiene sus puntos extremos en los mismos lugares
que la función original), es más sencillo bajar los exponentes antes de buscar el o los
máximos. Luego se deriva con respecto a
µ
σ 2 , se igualan a cero esas derivadas,
ya
se encuentran los valores que satisfacen cada ecuación y luego se verifican las condiciones de segundo orden. Tomando logaritmo natural en (2) y recordando las
propiedades de los logaritmos: exponente por el logaritmo de la base, el ln(e) es igual
a 1, etc.
ln( L) = −
n
2
ln(2πσ
En esta función, al derivar con respecto
µ
2
1
)− ∑
2
ya
( xi − µ ) 2
σ2
σ2,
∂ ln( L)
2
= 0 + 2 ∑( xi − µ )
2σ
∂µ
n 2π
1
1
∂ ln( L)
=− .
− (− 2 2 ∑( xi − µ ) 2
2
2
2 2πσ
2
(σ )
∂σ
Simplificando:
∂ ln( L) 1
= 2 ∑( xi − µ )
σ
∂µ
∂ ln( L)
n
1
= − 2 + 4 ∑( xi − µ )2
2
∂σ
2σ
2σ
Al imponer la condición de anular estas derivadas, se obtienen dos ecuaciones, siendo
los valores de µ y σ que las verifican los estimadores que buscamos: (no verifica2
mos aquí el resto de condiciones, puede hacerlo usted).
1
σˆ 2
−
∑( xi − µˆ ) = 0
n
1
+ 4 ∑( xi − µˆ )2 = 0
2
2σˆ
2σˆ
Despejando (observar que calculando el denominador común y luego multiplicando
ambos miembros por ese denominador común, éste “desaparece” al multiplicarse por
cero el segundo miembro):
18
Cátedra I Estadística II
Autor I Hebe Goldenhersch
∑ ( x - µˆ ) = 0 ;
i
∑x
i
µˆ =
n
n
1
−
+
∑ ( xi − µˆ ) 2 = 0;
2
4
2σˆ
2σˆ
− nσˆ 2 + ∑ ( xi − µˆ ) 2
= 0;
4
2σˆ
σˆ 2 =
∑ ( xi − µˆ ) 2
n
Así hemos comprobado que los estimadores “máximo verosímiles” de la media y
varianza en una población normal, son respectivamente la media muestral y la
varianza muestral sin corregir.
Los estimadores máximo verosímiles tienen, en general, las propiedades deseables
planteadas más arriba, es por ello que suelen resultar los mejores estimadores de los
diferentes parámetros en casi todos los casos. No obstante, el estimador máximo
verosímil de la varianza es un estimador sesgado, y por eso en lugar de usar
directamente el estimador máximo verosímil en general se corrige para que
desaparezca el sesgo (dividiendo por n-1 en lugar de n).
También puede verificarse que en una población Poisson, la media muestral es el
estimador máximo verosímil de la media poblacional; en una población dicotómica la
proporción muestral es un estimador máximo verosímil de la proporción poblacional (el
ejemplo de los profesores muestra esta situación). Estos problemas se plantean en las
Actividades que siguen.
Actividad 4:
Una compañía aseguradora está convencida de que el número de siniestros de
determinado tipo, que se producen semanalmente, se ajusta a un modelo
Poisson. Contando con una muestra de 7 semanas en las que se produjeron 59
siniestros, se desea obtener la estimación (es decir el valor) máximo verosímil del
promedio de siniestros semanales (λ) del modelo.
Recordar que:
f ( xi , λ ) =
λx
e- λ
i
xi!
Actividad 5:
Para la función de verosimilitud o probabilidad conjunta L(P) adjunta:
a) Determine el estimador máximo verosímil de P (proporción poblacional de
éxitos).
L(P) = Cnx .P x (1 − P) n − x
donde x = Σ xi
b) Explicite el modelo que representa la distribución poblacional y la muestral.
Actividad 6:
Se conoce que el coeficiente intelectual de las personas es una variable aleatoria
continua que se distribuye en forma normal. Sean x1, x2, .... xn los valores de
coeficientes observados en una muestra aleatoria de n individuos, ¿cuáles son los
estimadores máximo verosímiles de los parámetros de esta distribución?
19
Cátedra I Estadística II
Autor I Hebe Goldenhersch
En el punto anterior se desarrollaron los conceptos vinculados con la definición de
estimadores, sus propiedades deseables, los métodos para obtener buenos
estimadores, y se plantearon algunos estimadores que gozan de aquellas propiedades
y son utilizados en los problemas de aplicación más frecuentes: media muestral,
varianza muestral, proporción muestral.
Ahora bien, las estimaciones realizadas en forma puntual, esto es, calculando para
cada caso particular el valor surgido de una muestra, no llevan asociada idea alguna
acerca del grado de aproximación que puede existir entre el valor del estimador y el
del parámetro que se está estimando. O dicho de otra forma, no es posible conocer
algo acerca del "error " que puede cometerse al afirmar que el parámetro desconocido
se "estima " igual a esa función de las observaciones muestrales definidas por cada
estimador, ni de la confianza que puede depositarse en la sospecha de que el valor
estimado se encuentra relativamente cerca del parámetro desconocido.
Así por ejemplo, si se desea estimar la duración media de un lote de lamparitas
eléctricas; se toma una muestra de 25 lamparitas, y se las deja encendidas hasta
que se queman; si la duración media de esa muestra fue de 1200 horas, ¿qué
podemos decir acerca de la duración promedio de todo el lote, o sea su media
poblacional? Sólo que, si la muestra fue tomada al azar, y por lo tanto es
representativa de la población, deberíamos esperar que esa media no esté muy
lejos de las 1200 horas. Pero ¿cuánto es “no muy lejos”?
Precisamente, la diferencia existente entre el valor del estimador en una muestra
particular (a este valor lo hemos llamado “estimación”) y el verdadero valor del
parámetro desconocido se llama “error de muestreo”, nombre que es intuitivamente
comprensible. En efecto, si
de
θ
θ
es el parámetro que se desea estimar, y un estimador
, la expresión:
θˆ − θ ≤∈
ella indica
que el “error” cometido al realizar la estimación no excederá en valor
absoluto a ∈ . El error es aleatorio, porque depende de θ que es una variable aleatoria.
Esto significa que obviamente no es posible saber con exactitud en cuánto nos
“equivocaremos” al estimar un parámetro a partir de una muestra (este cuánto es una
variable aleatoria), pero la expresión que comentamos, está planteando la necesidad o
la intención que el error no supere a ∈ .
ˆ
Es interesante entonces, teniendo en cuenta el conocimiento de las distribuciones de
probabilidad de algunos estimadores y/o estadísticos8/, esto es, funciones de los estimadores y los parámetros, analizar la posibilidad de establecer un intervalo aleatorio,
( θˆ − ∈, θˆ + ∈ ), cuya amplitud es igual al doble del error máximo de estimación, y al cual
pueda asociarse una elevada probabilidad que el parámetro
8/
θ
sea interior al intervalo.
Si bien para muchos autores Estimador y Estadístico son sinónimos, nosotros hemos llamado
“estimador” a una función de las observaciones muestrales (por ejemplo, la media muestral) y
llamaremos “estadístico” a una función de las observaciones muestrales (generalmente a
través de un estimador) y también de parámetros poblacionales. Por ejemplo
x −µ
σ
es, para
n
nosotros un estadístico (es función de la media muestral, de la media poblacional y de la
desviación estándar poblacional).
20
Cátedra I Estadística II
Autor I Hebe Goldenhersch
De esta manera, si por ejemplo se desea estimar el tiempo promedio que demoran
los proveedores de una línea de productos para entregar los pedidos, al efectuar la
estimación puntual, podrá concluirse que la demora promedio, según lo calculado a
partir de la media muestral, es de 12 días. Si se realiza una estimación por
intervalo, utilizando el conocimiento existente acerca de la distribución de la media
muestral, podría concluirse que existe una confianza del 95% que la demora
promedio se encuentre en el intervalo (10,5 - 13,5) días.
Podemos decir que, si bien se ha perdido precisión en la estimación al referirse la
misma a un intervalo y no a un valor puntual, se ha ganado en el conocimiento
del error que puede cometerse al realizarla (en este caso, la diferencia entre el
verdadero valor del parámetro y el de su estimación no supera 1,5 días) y del
grado de confianza (probabilidad fiducial se llama este grado de confianza; se
explicará más adelante por qué no es estrictamente una probabilidad) que la
afirmación sea verdadera (en este caso, existe un 95% de confianza que el
verdadero promedio se encuentre entre 10,5 y 13,5 días, y hay sólo un 0,05 de
probabilidad que ello no ocurra, esto es, que el verdadero promedio no se ubique
en ese intervalo).
5.1. Desarrollo de un ejemplo
21
Cátedra I Estadística II
Autor I Hebe Goldenhersch
A partir de la necesidad de estimar la media poblacional se desarrollará un ejemplo, teniendo en cuenta el conocimiento que existe de la distribución de la media
muestral.
Para este ejemplo se plantearán algunos supuestos, que pueden resultar irritantes;
habrá quienes digan: "esos supuestos no se verifican nunca...", o "cómo hago para
saber si se cumplen los supuestos". Sin embargo, más adelante al desarrollar los
diferentes casos, se irán levantando algunos de estos supuestos, y también aprendiendo los procedimientos para saber si se cumplen o no en diferentes poblaciones.
Se trata de estimar la media de una variable en cierta población, de la cual se
conoce que tiene distribución normal, y además se supone conocida la varianza
poblacional la reacción de algunos podrá ser: "pero, si no conozco la media, cómo
voy a conocer la varianza..."!. El conocimiento de la varianza puede provenir de
experiencias anteriores con poblaciones similares (hay mayor permanencia en la
varianza que en la media). Ambos supuestos (población normal y varianza
conocida) serán levantados en desarrollos posteriores. La estimación se efectuará
a partir de una muestra aleatoria de tamaño n.
El estimador puntual de µ es X . Por tratarse de una población normal, no importa
cuál sea n, (¿recuerda por qué?) se conoce que la distribución de X es también
normal, con esperanza
µ
y varianza
σ
2
X −µ
σ
n . Luego, el estadístico:
~ N (0,1),
n
Observe que el estadístico planteado, es función del estimador, del parámetro a
estimar y de σ , pero habiendo supuesto conocida esta última, µ es la única incóg-
nita de la expresión, n es el tamaño de la muestra, y el valor particular del estimador X se obtendrá a partir de la muestra. El conocimiento de la distribución de
probabilidad del estadístico, permite afirmar que:

X −µ

σ
P  zα 2 <

n
< z1−α 2  = 1 − α

(3)
y se lee: existe una probabilidad igual a 1- α que el estadístico esté comprendido
entre Z α 2 y z1−α 2 . Recordando los valores de la variable normal estandarizada, se
advierte que los límites izquierdo y derecho del intervalo, son –z y z . Esta z es la
abscisa de la curva normal (0,1) correspondiente a una probabilidad acumulada
igual a 1 − α 2 . Así por ejemplo, si 1 − α = 0.95, entonces z = 1,96 dado que
P(z < 1.96) = 0.975 y P(- 1,96 < z < 1,96) = 0,95.
Normal (0.1)
0.95
0
-1.96
22
1.96
Z
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Despejando el error aleatorio en (3):
P(− z σ X
n < X − µ < zσX
n ) = 1 − α (4)
Esto se lee: existe una probabilidad igual a 1- α que el error (aleatorio, porque
depende de X ) de estimación no supere en valor absoluto a z σ
n . Como puede
observarse la probabilidad 1- α , que debe ser elevada (generalmente mayor a
0,90) es la que determina el valor de z: a mayor “confianza”, es decir mayor 1- α ,
mayor será z y eso incidirá aumentando el valor máximo del error (se tendrá una
estimación menos precisa); a mayor tamaño de muestra, será menor el error
estándar del estimador ( σ
n ) y por lo tanto será menor el error máximo de
estimación (se tendrá una estimación más precisa).
Ahora despejando en la expresión (4):
P( X − z σ
n < µ < X + zσ
n = 1 − α (5)
Observe: ¿dónde está la variable aleatoria en esta expresión probabilística? ¿ µ es
una variable aleatoria?
...Entonces debe leerse: existe una probabilidad igual a 1- α que el intervalo
aleatorio X − z σ
bilidad que
n , X + zσ
n contenga a µ (y no es correcto hablar de proba-
µ esté comprendida... etc.).
Se recomienda leer varias veces y muy atentamente los párrafos destacados en
gris, hacerse preguntas e intentar responderlas, ya que son fundamentales para
comprender el concepto de estimación por intervalos.
El intervalo X ± z σ
n es un intervalo de confianza del
(1 − α ) . 100  % para µ
.
La expresión intervalo de confianza se debe a que, una vez tomada la muestra y
realizada la estimación de µ obteniendo una media muestral particular, el
intervalo deja de ser aleatorio, y toma dos valores también particulares, llamados
límite inferior y límite superior de confianza, y el nivel 1- α expresa ya no una
probabilidad, porque no hay ninguna variable aleatoria a la cual referir esa
probabilidad, sino un nivel de confianza que el intervalo obtenido contenga al
parámetro conocido:
LIC = x − z σ
n
LSC = x + z σ
n
El gráfico que sigue, puede ayudar a comprender cabalmente el significado de los
límites de confianza en una estimación. De acuerdo al ejemplo planteado, se trata
de una distribución normal, con media µ y desviación estándar σ . Se grafica la
distribución de la media muestral para muestras de tamaño n que por lo tanto es
también normal, con media µ , y desviación estándar σ
n.
El intervalo señalado en el gráfico, encierra el 0,95 de probabilidad debajo de la
curva normal. Esto es, el 95% de las posibles muestras aleatorias de tamaño n,
tendrán una media dentro de ese intervalo. El intervalo de confianza que se
construye a partir de una media muestral, consiste en restar y sumar a ella la
cantidad 1, 96.σ
n.
23
Cátedra I Estadística II
Autor I Hebe Goldenhersch
------------------------------
x1
LIC
LSC
------------------------------
x2
LIC
LSC
------------------------------
x3
LIC
LSC
------------------------------
x4
LIC
LSC
------------------------------
LIC
x5
LSC
Como puede observarse en las líneas trazadas debajo de la curva normal, correspondientes a los posibles resultados de cinco muestras, siempre que la media
muestral caiga dentro del intervalo del 0,95 de probabilidad, los límites de
confianza contendrán en su interior la media poblacional µ .
Es decir, el intervalo así construido encerrará la verdadera media (aunque ésta
sigue siendo desconocida, se sabe que el intervalo la contiene). Pero cuando la
media muestral cae fuera del intervalo del 95% (¿en qué porcentaje del total de
muestras posibles se espera que esto ocurra?...) los límites de confianza obtenidos
no contendrán la verdadera µ .
Luego, cuando se tome una muestra aleatoria, y a partir de la media de esa
muestra se
construya un intervalo de amplitud igual al doble de 1, 96.σ
n , se
tendrá una confianza igual a (1 − α ).100% (95% si z = 1,96) que el valor del
parámetro µ , desconocido, esté dentro de ese intervalo. (¿Cuánto debe valer z si
se desea una confianza del 98%? ¿y del 90%?)9/.
En este ejemplo gráfico, de cinco muestras obtenidas, sólo en la cuarta resulta un
intervalo que no contiene a µ . En las restantes, es "verdadera" la afirmación
que µ se encuentra entre el LIC y el LSC.
¿Comprende ahora qué significa 95% de confianza?... ¿Es correcto afirmar que el
máximo error que puede cometerse al realizar la estimación de la media en este
caso es 1, 96.σ
9/
n ? ¿Por qué?
Para el 98% es z = 2,326; para el 90% es z = 1,645 (¿los encontró usted en la tabla?).
24
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Para precisar el ejemplo planteado más arriba acerca del tiempo de demora para
entregar los pedidos, supóngase conocida la varianza poblacional ( σ = 4). Se
2
toma una muestra de 49 pedidos, y se encuentra una media muestral de 8 días.
Luego, para un 95% de confianza:
P ( X − 1, 96. σ
n < µ < X + 1, 96 σ
n = 0, 95
Hay una probabilidad de 0.95 que el intervalo expresado arriba, contenga la
demora promedio. Se trata de un intervalo aleatorio. Luego remplazando por
los datos del problema:
LIC = (8 − 1, 96. 2
49) = 7, 44
LSC = (8 + 1, 96. 2
49) = 8, 56
Esto significa: existe un 95% de confianza que la demora promedio para entregar
un pedido, se encuentre entre 7,44 y 8,56 días.
Es importante reflexionar acerca de la amplitud del intervalo (también se llama
“precisión de la estimación”, sólo que varían en sentido inverso, mayor precisión
implica menor amplitud). Quien construye un intervalo de confianza, desea que
además de una elevada “confianza” en la exactitud de su afirmación, el intervalo
sea lo más preciso posible, porque un intervalo muy amplio, dice poco acerca del
parámetro a estimar.
5.2. Planteo general de la estimación por intervalos
Teniendo en cuenta el desarrollo del ejemplo en el punto anterior, puede describirse el
procedimiento general para la construcción de intervalos de confianza, siguiendo los
pasos siguientes:
1) Establecer cuál es el parámetro θ , desconocido, y qué se conoce de la población.
2) Buscar un estimador puntual θ
ˆ = g ( x , x ... x )
1
2
n función
de las observaciones
muestrales en una muestra de tamaño n.
3) Plantear, de acuerdo a lo establecido en los dos puntos anteriores, un estadístico
función del estimador y del parámetro h (θˆ, θ ) . Dicho estadístico debe cumplir dos
condiciones: primera, que algebraicamente sea posible despejar el párametro única incógnita de la expresión y segunda, que tenga una distribución
de probabilidad conocida (y en lo posible tabulada). En el ejemplo planteado
anteriormente, el parámetro era µ , la población normal con varianza conocida, el
estimador X , el estadístico ( X − µ ) (σ
n ) , en el cual se advierte claramente
que, por los supuestos establecidos µ es la única incógnita, y además tiene una
distribución que es conocida: N (0,1).
4) En estas condiciones, fijando el nivel de confianza 1 − α , el cual indica la probabilidad que el intervalo así construido contenga realmente al parámetro poblacional,
se determina en primer lugar un intervalo para el estadístico:
P ( k1 < h(θˆ, θ ) < k 2 ) = 1 − α
k
k
Donde 1 y 2 se obtienen teniendo en cuenta la distribución de probabilidad del
estadístico y el nivel de confianza establecido. En el ejemplo este intervalo es:

X −µ

σ
P  zα 2 <
n

< z1−α 2  = 1 − α
25

Cátedra I Estadística II
Autor I Hebe Goldenhersch
5) Luego se despeja el parámetro, obteniéndose un intervalo aleatorio el cual tiene
una probabilidad igual a 1-α de contenerlo. En el ejemplo:
P ( X − 1, 96. σ
n < µ < X + 1, 96 σ
n = 0, 95
6) Por último y ya con los valores particulares de una muestra, se realiza la
estimación del parámetro, y se obtienen los límites inferior y superior de confianza
entre los cuales se piensa con una confianza igual a (1 − α ) 100% que se encuentra
θ . En el ejemplo:
LIC = (8 − 1, 96. 2
49) = 7, 44
LSC = (8 + 1, 96. 2
49) = 8, 56
Se trata ahora de obtener intervalos de confianza para la media de una población,
aplicando el método general descripto en 5.2. Se plantean distintos casos, según el
conocimiento que se tenga de la población, el tamaño de la muestra, y los
supuestos que pueden realizarse acerca de la distribución poblacional.
En todo lo que sigue, se supone un muestreo aleatorio simple (con reemplazo). Si se
trata de poblaciones finitas, y el muestreo es sin reemplazo, debe corregirse el error
estándar de la media muestral, multiplicando σ
n por
( N − n ) ( N − 1)
10/
.
Consideraremos los siguientes casos:
Varianza poblacional conocida
Varianza poblacional desconocida
Intervalos de confianza para la proporción poblacional
Intervalos de confianza para la varianza en poblaciones normales.
6.1. Varianza poblacional conocida
Este primer caso coincide con el desarrollado en el ejemplo. Siendo µ el parámetro a
estimar, conociendo la varianza poblacional, se advierte de inmediato que el estimador
será la media muestral, y el estadístico a utilizar.
X −µ
σ
~ N (0,1)
(6)
n
siempre que:
•
Se trate de una muestra extraída de una población normal (por tratarse de una
combinación lineal de variables normales) se distribuye N ( µ , σ
n) y el estadístico
es N(0,1).
O bien
•
Se trate de muestras grandes (n> 30) extraídas de cualquier población. Entonces
por aplicación del Teorema Central del Límite, también X se distribuye
N (µ , σ
10/
n) y el estadístico es N(0,1).
Recordar el factor de corrección de la varianza en la Distribución Hipergeométrica (muestreo
sin reemplazo).
26
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Si la población no es normal, y la muestra es menor que 30, no puede usarse este
estadístico (algunas alternativas: utilizar la desigualdad de Chebycheff para obtener el
intervalo de confianza, o bien realizar alguna transformación con la variable para que
la distribución poblacional de la variable transformada se aproxime a la normal. En
otros Capítulos se comentará acerca de las transformaciones posibles).
Actividad 7:
El dueño de una estación de servicio desea saber la cantidad de nafta diaria que
vende, en promedio, por cliente. Toma una muestra al azar de 36 clientes y
encuentra que, en promedio vendió 15 litros de nafta. Si sabe por estudios
anteriores que la población se distribuye aproximadamente normal con una
desviación estándar de 2 litros, se pide encontrar:
a) La estimación puntual de la media poblacional.
b) Un intervalo de confianza del 95% para la media de la venta diaria de
combustible en dicha estación de servicio.
c) Si luego se conociera que la media poblacional es de 14 litros ¿qué pudo haber
pasado?
d) Un intervalo de confianza del 99%. Explique la diferencia con el obtenido en
b).
Modificando el enunciado del ejercicio como sigue, vuelva a resolverlo, y
reflexione acerca de las diferencias con el anterior. Los resultados que se
reproducen, así como varios de los ejercicios siguientes corresponden a
salida de máquina de un procesamiento realizado con un paquete
estadístico. Es necesario que los estudiantes se habitúen a interpretarlos.
El dueño de una estación de servicio desea saber la cantidad de nafta diaria que
vende, en promedio, por cliente. Toma una muestra al azar de 136 clientes y
encuentra:
Estadística descriptiva
Resumen
n
Media
Var(n-1)
E.E.
Mín
Máx
Mediana
Q1
Q3
nafta
136
15
3,97
0,17
10
22
15
14
16
a) ¿Puede indicar algún estimador para el parámetro de interés?
b) Con un nivel de confianza del 95%, ¿qué límites de estimación propone para
dicho parámetro?
6.2. Varianza poblacional desconocida. Población normal
Si se desconoce la varianza poblacional, el estadístico planteado en el punto anterior
no puede ser aplicado, ya que existirían dos parámetros desconocidos: µ y σ .
Hay una solución para este problema. ¿Recuerda de Estadística I la distribución del
estadístico:
X −µ
S
?
(7)
n
S es la desviación estándar corregida, estimada a partir de la muestra.
27
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Ese estadístico tiene distribución t con n-1 grados de libertad.
Si la muestra es grande, la función de densidad de la t se aproxima a una normal,
por lo tanto, los límites de probabilidad pueden ser los correspondientes a la distribución normal.
Pero también es importante recordar que para aplicar la distribución t, necesariamente
se parte de una distribución poblacional normal. Luego, si la varianza poblacional es
desconocida, pueden construirse intervalos de confianza utilizando el estadístico
siempre que la población sea normal, cualquiera sea el tamaño muestral.
¿Qué pasa si la población no es normal? Nuevamente se presentan algunas
alternativas:
•
•
•
Intentar alguna transformación de la variable original para aproximarla a una
normal (en distribuciones asimétricas con “cola derecha” la transformación
logarítmica o la raíz cuadrada suelen proporcionar buenas aproximaciones a la
normalidad). Esto significa que se calcularán intervalos de confianza para el
logaritmo o para la raíz de la variable, lo cual a veces complica la interpretación;
Si las muestras son suficientemente grandes -estamos hablando de
poblaciones no normales- (en general es suficiente con n > 100), teniendo en
cuenta que S es un estimador consistente de σ , puede usarse el estadístico (6),
utilizando la S muestral en lugar de la a poblacional. Esto, recalcamos, sólo puede
hacerse con muestras bastante grandes porque de lo contrario, con poblaciones no
normales y varianza poblacional desconocida, los intervalos resultantes no tienen
la confianza esperada.
Si la muestra no es mayor que 100, y no puede hacerse una transformación
adecuada de la variable para “normalizarla”, deberá recurrirse a la desigualdad de
Chebycheff. En realidad, este procedimiento no es aconsejable, porque los
intervalos resultantes de aplicar la desigualdad de Chebycheff son muy poco
precisos.
Actividad 8:
Una compañía, dedicada a la venta de productos derivados del petróleo desea
realizar un estudio de mercado para estimar la cantidad gastada, por año, en
combustible para calefacción casera en una determinada ciudad. Una muestra de
64 hogares arrojó como resultado una
y
= $ 836 y una s = $ 178. Encontrar un
intervalo de confianza del 90% para el verdadero gasto promedio anual en
combustible, en las viviendas de esa ciudad y suponiendo que dicho gasto tiene
una distribución aproximadamente normal.
Actividad 9:
Debido a que el estudio de la duración de focos de luz implica la destrucción de los
mismos, con el análisis de una muestra aleatoria de n = 10 focos de una nueva
marca lanzada al mercado, ¿qué puede decir de la duración de esta nueva marca,
a un nivel de confianza del 95%?
Vida útil (en hs.)
4402
4066
3788
4028
3973
3629
4275
3944
4090
3913
28
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Intervalos de confianza
Estimación paramétrica
Variable
vida útil
Parámetro
Media
Estimación
4010,80
E.E.
70,18
n
10
LI(95%)
3852,03
LS(95%)
4169,57
Box plot
4440,65
vida ú til
4228,07
4015,50
3802,92
3590,35
vida útil
Actividad 10:
Una editorial que lanza al mercado un nuevo diario desea estimar la cantidad
diaria promedio a imprimir. Una muestra aleatoria de 7 días mostró una demanda
promedio de 2500 ejemplares y una desviación típica muestral de 238.
Suponiendo que la distribución de la demanda diaria es normal, determinar un
intervalo de confianza del 99% para la media poblacional.
Actividad 11:
El directorio de una empresa ferroviaria desea estimar, a un nivel de 0,95, el
tiempo diario promedio que han trabajado los 2000 empleados de esa empresa
durante el año anterior. Como el examen de los 2000 legajos insumiría mucho
tiempo y personal, se decidió tomar una muestra simple al azar de 50 legajos, sin
reposición. Por estudios anteriores se sabe que el tiempo trabajado se distribuye
aproximadamente normal. Los resultados obtenidos de la muestra fueron los
siguientes:
xi
= tiempo trabajado en la Cía. por el i-ésimo empleado seleccionado,
durante un día determinado.
= 300 hs.
Σxi
2
Σ xi
= 2835,50 hs.
Actividad 12:
Para determinar el rendimiento anual de ciertas acciones, un grupo de inversores tomó una muestra de n = 50. La media y desviación estándar resultaron
y
= 8,71% y s = 2,1%. Suponiendo que el rendimiento de esta clase de acciones
se distribuye en forma aproximadamente normal, estimar su verdadero rendimiento anual promedio usando un intervalo de confianza del 90%.
Actividad 13:
Una empresa dedicada a la venta de productos derivados del petróleo está
elaborando su plan de negocios para el próximo año. Sobre la base de un estudio
de mercado del gasto anual en combustible (en $) de un conjunto de hogares se
29
Cátedra I Estadística II
Autor I Hebe Goldenhersch
obtuvo la siguiente información. ¿Cómo podría utilizar el intervalo de confianza
construido?
Intervalos de confianza
Estimación paramétrica
Variable
Combustible
Parámetro
Media
Estimación
857,87
E.E.
24,51
n
64
LI(90%)
816,95
LS(90%)
898,79
C uan tile s ob s e rva do s (C o m bu s tible)
Q - Q p lo t
1 3 1 6 ,0 5
n = 6 4 r = 0 ,9 8 9 ( C o m b u s tib le )
1 0 8 3 ,4 6
8 5 0 ,8 7
6 1 8 ,2 8
3 8 5 ,6 9
3 8 5 ,6 9
6 1 8 ,2 8
8 5 0 ,8 7 1 0 8 3 ,4 6 1 3 1 6 ,0 5
C u a n ti l e s d e u n a N o r m a l ( 8 5 7 ,8 7 ,3 8 4 4 7 )
C o m b u s tib le
Recuerde que con el gráfico Q-Q plot puede analizar si la variable en estudio
tiene distribución normal (este gráfico completa una prueba de hipótesis
paramétrica que se estudiará en el Capítulo VI).
Histograma
fre cue ncia s relativas
0,26
Ajuste: Normal(857,870,38447,088)
0,20
0,13
0,07
0,00
332,88
570,55
808,22
1045,88 1283,55
Combustible
Combustible
6.3. Intervalos de confianza para la proporción poblacional
n
x
=
p
Sea una población dicotómica, con N elementos, de los cuales k tienen una determinada propiedad. Luego p = k/N es el parámetro (desconocido) que pretendemos
estimar a partir de una muestra tamaño n. El estimador de p es
ˆ
, donde x es
el número de elementos en la propiedad deseada (éxitos) en la muestra.
Recuérdese que x tiene distribución binomial, con esperanza np y varianza np(1-p).
El estadístico a utilizar dependerá del tamaño de la muestra.
30
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Muestras chicas
En este caso será necesario utilizar la distribución binomial, para encontrar un intervalo de confianza para k (número de “éxitos” en la población), y a partir de k se obtiene
p. Debido a que se trata de una distribución discreta, y que las tablas están construidas para p que varía de 0,05 en 0,05, los intervalos resultan sólo aproximados.
Para solucionar este problema, se han publicado los llamados “cinturones de confianza
para p” que se pueden consultar en la publicación que contiene las tablas estadísticas
usadas en la Facultad (páginas 43 y 44). En ellas hay cinturones de confianza para el
95 y para el 99%. A continuación explicamos cómo se obtienen en forma gráfica los
intervalos de confianza del 95% para p, conociendo el valor observado de x/n11/.
Se ingresa en el gráfico de acuerdo a este último valor (por el eje de las abcisas), y se
buscan las ordenadas correspondientes al límite inferior y superior de confianza para p
de acuerdo al tamaño de la muestra. Para cada tamaño de muestra, se dibuja un
“cinturón”. Por ejemplo, si en una muestra de tamaño 50 se encontraron 20 éxitos
pˆ = 0, 4 aproximadamente LIC = 0.27, LSC = 0.54 (aproximadamente, porque se determinan los valores gráficamente en la escala de p que sólo tiene las divisiones
correspondientes de 0.10 en 0.10).
Con este y algún otro ejemplo que sugerimos plantear, podrá observar la gran amplitud de los intervalos obtenidos a partir de la distribución binomial (o los cinturones
de confianza); esto equivale a una baja precisión de las estimaciones, y por lo tanto su
utilización no resulta en general práctica, de allí la necesidad de trabajar con
muestras relativamente grandes cuando se desean estimar proporciones.
Muestras grandes
Por el Teorema Central del Límite, se utiliza el estadístico:
pˆ − p
p (1 − p ) n
~ N (0,1)
(8)
siempre que n sea suficientemente grande. Existe una evidencia empírica, de que la
aproximación es buena cuando np > 5 y n(1-p) > 5.
Deben cumplirse ambas desigualdades. Si alguna de ellas no se cumple, la aproximación normal no es buena y deben utlilizarse los cinturones de confianza.
Al despejar p, resulta un intervalo con probabilidad 1 − α de contener al parámetro:
pˆ − z p (1 − p ) n < p < pˆ + z p (1 − p ) n
El problema es que los límites de confianza contienen el parámetro desconocido. Hay
que trabajar bastante para despejar completamente p, resolviendo una ecuación de
segundo grado... Pero ocurre que se logra una buena aproximación de manera más
sencilla, teniendo en cuenta que siendo n bastante grande, en la solución aparecen
términos con n ó n al cuadrado en el denominador, que son próximos a cero. Al
despreciar esos términos, resultan los límites:
LIC = pˆ − z
11/
pˆ .(1 − pˆ ) n y LSC = pˆ + z
pˆ .(1 − pˆ ) n
No obstante, es conveniente aclarar, y usted mismo observará, que los intervalos obtenidos
son muy amplios (muy poco precisos), por lo que en la práctica se utilizan poco. La razón de
esta gran amplitud, es que la varianza (y también el error estándar) de la proporción es muy
alta cuando n no es suficientemente grande. Como en este punto estamos tratando con
muestras chicas, necesariamente los errores estándar son grandes. La solución es, entonces,
tomar muestras más grandes, y en ese caso se pasa a trabajar con la distribución normal, tal
como se explica en el punto siguiente.
31
Cátedra I Estadística II
Autor I Hebe Goldenhersch
lo cual es equivalente a utilizar el estadístico (8), reemplazando en el denominador p
por p̂ ’.
¿Se anima a despejar el intervalo exacto para p a partir del estadístico (8)?
Incorporamos además cuatro Actividades de resolución de problemas respecto
del tema que venimos tratando.
Actividad 14:
Ante los reiterados rechazos de productos que una fábrica de radiadores recibe
por parte de sus clientes, el jefe de producción decide estimar el verdadero
porcentaje de defectuosos que sale de la planta. En caso de que dicho porcentaje
supere el 15% está dispuesto a realizar los ajustes que fueran necesarios en el
proceso de producción. Con este fin toma una muestra aleatoria de 120
radiadores encontrando que 12 de ellos tenían algún defecto. ¿Debe el jefe de
producción realizar algún ajuste? Use (1 - α) = 0,90.
Actividad 15:
El auditor de una gran empresa encuentra que, de 1500 cuentas por cobrar
controladas, 450 se encuentran con su saldo vencido. En base a estos datos se
decide a estimar p, proporción verdadera de todas las cuentas por cobrar que
están vencidas, mediante un intervalo de confianza del 95%.
Actividad 16:
Tomada una muestra al azar de 500 directores de empresa se encuentra que 100
de ellos habían pasado sus vacaciones en el exterior. Estimar la proporción
poblacional de directores de empresa que vacacionan en el extranjero mediante
un intervalo de confianza del 99,73%.
Actividad 17:
Un grupo de docentes de la Facultad de Ciencias Económicas desea conocer el
porcentaje de estudiantes que se dedicarían a la docencia luego de egresados.
Una muestra aleatoria de 100 estudiantes arrojó que 39 de ellos elegirían la
docencia.
a) Obtenga alguna conclusión a partir de los datos siguientes.
b) Un menor nivel de confianza, ¿mejoraría la precisión de la estimación?
Intervalos de confianza
Estimación paramétrica
Variable
docencia
Parámetro
Proporción(>0)
Estimación
0,39
E.E.
0,05
n
100
LI(99%)
0,26
LS(99%)
0,52
Parámetro
Estimación
Proporción(>0)
0,39
E.E.
0,05
n
100
LI(95%)
0,29
LS(95%)
0,49
Intervalos de confianza
Estimación paramétrica
Variable
Docencia
6.4. Intervalos de confianza para la varianza en poblaciones normales
Cuando se trata de estimar la varianza poblacional, recuérdese que el estimador
insesgado es la varianza muestral (corregida)
(n − 1) S
σ
S 2 y que el estadístico es:
2
2
32
~ χ n2−1
Cátedra I Estadística II
Autor I Hebe Goldenhersch
χ n2−1 , se construye el intervalo para el estadístico:
Luego, a partir de la distribución
P ( χα
2
Los valores χα
2
y χ 1− α
<
σ
2
2
< χ 1− α 2 ) = 1 − α
2
corresponden a la distribución χ con n-1 grados de libertad,
2
2
2
2
( n − 1) S
2
dejando a la izquierda de χα
una probabilidad igual a α 2 y a la derecha de χ1−α
2
2
2
2
una probabilidad similar12/.
Al despejar el parámetro
σ 2 , resultan los límites de confianza:
LIC =
(n − 1) S 2
χ12−α 2
LSC =
,
( n − 1) S 2
13/
χα2 2
Veamos la cuestión de modo práctico.
Actividad 18:
El departamento de Control de Calidad de una envasadora de lubricantes desea
conocer la varianza en el llenado de las latas de 4 lts. Interprete la salida que se
muestra a continuación:
Intervalos de confianza
Estimación paramétrica
Variable
llenado latas
Parámetro
Varianza
Estimación
0,02
E.E.
0,01
n
27
LI(90%)
0,01
S(90%)
0,03
Stem-and-Leaf Plot
Frequency Stem
1,00 Extremes
1,00
35 .
2,00
36 .
9,00
37 .
8,00
38 .
5,00
39 .
1,00
40 .
Stem width:
Each leaf:
12/
13/
& Leaf
(=<3,41)
5
57
224556799
02344699
44667
9
, 10
1 case(s)
A pesar que aquí no se ha demostrado la conveniencia de construir intervalos simétricos
cualquiera sea la distribución, debe mencionarse que ello es conveniente a fin de minimizar la
amplitud de los intervalos de estimación. Esta simetría se entiende en el sentido de dejar
fuera del intervalo una probabilidad igual en cada cola. Cuando la distribución es simétrica,
como en el caso de la normal o la t de Student, también el intervalo resultará simétrico
alrededor del parámetro; de lo contrario, como ocurre en este caso, donde la distribución no
es simétrica, el intervalo tampoco lo es , pero su amplitud será la menor posible (mayor
precisión).
Observe que en el proceso algebraico de despejar, los valores de tabla χ se invierte, el mayor
2
va en el denominador del LIC y el menor en el denominador del LSC.
33
Cátedra I Estadística II
Autor I Hebe Goldenhersch
C uantiles obs ervados (llenado latas )
Q-Q plot
4,09
n= 27 r= 0,974 (llenado latas )
3,92
3,75
3,58
3,41
3,41
3,58
3,75
3,92
4,09
C uantiles de una N orm al(3,8037,0,019381)
Actividad 19:
Un agente de bolsa debe asesorar a un nuevo inversor con relación al precio de
las acciones de un banco, no sólo en su promedio de cotización sino también en
su variabilidad. Para ello computó los valores diarios de cotización durante los
primeros 24 días del mes anterior, obteniendo:
Día
1
2
3
4
5
6
7
8
Cotización
142,07
142,42
128,32
129,36
139,23
130,76
135,95
119,17
Día
9
10
11
12
13
14
15
16
Cotización
128,90
133,14
139,40
133,71
148,73
138,19
126,68
139,02
Día
17
18
19
20
21
22
23
24
Cotización
117,56
125,27
127,35
130,98
131,09
143,09
124,11
143,64
Cuantiles observados(cotizaciones)
Q-Q plot
148,92
n= 24 r= 0,991 (cotizaciones)
141,08
133,24
125,40
117,56
117,56 125,40 133,24 141,08 148,92
Cuantiles de una Normal(133,26,64,73)
cotizaciones
¿Qué información podrá dar el agente de bolsa a un nivel de 0,95?
34
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Actividad 20:
Para un determinado electrodoméstico, el promedio de ventas por comercio
durante el mes de Diciembre del año anterior, y de acuerdo con una muestra de
20 negocios, fue $ 3407 con una desviación de $ 219. ¿Qué puede decir de la
variabilidad de las ventas del electrodoméstico en ese mes, utilizando un nivel de
confianza del 90%?
C u antiles ob s ervado s (ve ntas )
Q-Q plot
3816,72
n= 20 r= 0,982 (v entas )
3609,64
3402,57
3195,49
2988,41
2988,41 3195,49 3402,57 3609,64 3816,72
C u a n tile s d e u n a N o rm a l(3 4 0 6 ,7 ,4 8 1 5 9 )
v entas
En Estadística I se ha mencionado la aproximación de la distribución χ a la normal
2
cuando el número de grados de libertad es suficientemente grande.
Una de las primeras preguntas que surge cuando se desea realizar una estimación de
parámetros a partir de una muestra, es naturalmente: ¿de qué tamaño debe
tomarse la muestra?
Tal vez ustedes han escuchado la expresión “para muestra
solía utilizarse para expresar que no es necesario tomar
conociendo un elemento de la población (un botón) se puede
(de los botones). ¿Es verdad esto, para los casos en que
parámetro de la población en estudio?
basta un botón” que
muestras grandes, si
saber cómo es el resto
uno desea conocer un
Algunos dirán que sí, la mayoría dirá que no… en realidad puede o no serlo: si todos
los botones son iguales (no hay variabilidad), ¿para qué tomar más de uno? ...
entonces sería verdadera la afirmación. Si hay cierta variabilidad entre los botones en
estudio, habrá que seleccionar más de uno, y si hay una variabilidad importante, habrá
que seleccionar muchos más para tener una idea de cómo es la población … Entonces,
antes de contestar si basta o no basta con un botón, hay que preguntarse por la
variabilidad …
De igual manera, la pregunta acerca del tamaño necesario de muestra, sólo puede
responderse con otras preguntas: ¿Cuál es el máximo error que se está dispuesto
a tolerar? ¿Cuál es el nivel de confianza deseado para las estimaciones? ¿Cuál
es la varianza de la población bajo estudio? ¿Se trata de muestreo con o sin
reemplazo?
En lo que sigue responderemos a la cuestión de cómo calcular el tamaño de
muestra para estimar la media de una población.
Comenzamos por el caso más general.
35
Cátedra I Estadística II
Autor I Hebe Goldenhersch
7.1. Muestreo con reemplazo, o en poblaciones infinitas. Estimación de la
media o de la proporción
Supóngase que se desea estimar la media de una población ( µ ), y que se conoce su
varianza. Si el nivel de confianza deseado es de 1 − α , entonces:
P ( zα
2
<
X −µ
σ
<
n
z1−α
2
) = 1−α
siendo X − µ el “error de estimación”, que hemos llamado e, al despejar resulta:
P( e
σ
< z.
) = 1−α
n
Esta expresión puede leerse: existe una alta probabilidad
estimación sea como máximo igual a z.
σ
(1 − α )
que el error de
.
n
Luego, e, igual a z.
σ
sería el “error máximo” de estimación, y despejando:
n
e
σ
= z.
n
z .σ
2
n=
e
2
2
(9)
Este es el tamaño de muestra necesario para que e sea el máximo error. Un n mayor
reducirá el error máximo.
Esta fórmula, permite conocer de qué tamaño deberá tomarse la muestra para que el
error no supere a e, eligiendo z de acuerdo con el nivel de confianza deseado. Debe
prestarse atención a que el tamaño muestral, depende del nivel de error aceptable
(e), del nivel de confianza deseado, reflejado en z y de la variabilidad de la variable
en la población ( σ ).
La aplicación de la fórmula que hemos analizado presenta algunos inconvenientes:
•
La necesidad de conocer la varianza poblacional. Esta situación es superada
en la práctica ya sea utilizando una varianza conocida por experiencias anteriores,
vinculadas con la misma variable o con alguna variable “Proxy” (modo en que los
economistas denominan a otra variable con comportamiento similar a la que se
tiene en estudio); estimándola a partir de una muestra piloto, o bien utilizando el
conocimiento que un experto pueda tener de la forma de la distribución
poblacional, y de los valores mínimo y máximo con que podrá encontrarse en la
muestra, aproximarse al valor del desvío estándar. Por ejemplo, si se conoce que
la población tiene una distribución aproximadamente normal, entre la media más y
menos tres desvíos estándar se encuentra prácticamente la totalidad de las
observaciones -99,73%-; luego conociendo el mínimo y el máximo valores
posibles, dividiendo por 6 se tendrá una aproximación al valor de σ . En otros
36
Cátedra I Estadística II
Autor I Hebe Goldenhersch
•
•
casos, y para no subestimar la varianza, lo cual influirá negativamente en el
tamaño muestral, suele dividirse por 4 el rango supuesto14/.
Por otra parte, el error en la fórmula (9) está expresado en forma absoluta, en las
unidades de la variable en cuestión (por ejemplo, $ 5, 3 metros, diez personas…).
Para poder evaluar cuándo un cierto nivel de error se considera elevado o
aceptable, es necesario relacionarlo con los valores posibles de la variable y de su
media (no es lo mismo un error de $ 100.- en más o en menos respecto de una
media igual a $ 10.000, que un error de $ 100.- en más o en menos respecto de
una media igual a $ 100.-). Este aspecto se resuelve efectuando un razonamiento
de este tipo, previo a la fijación del error máximo aceptable, o realizando los
cálculos con una medida de error relativo, tal como se considera más adelante.
En tercer lugar, cuando se realiza una investigación, generalmente se pretenden
estimar parámetros de varias variables: ¿a cuál de ellas hay que referirse para
calcular el tamaño de la muestra? Esta cuestión generalmente se resuelve
seleccionando la variable más relevante, o la que se supone de mayor variabilidad,
a fin de no subestimar el tamaño de la muestra.
¿Ha observado que el tamaño de la población (N) no aparece en la fórmula?
Reflexione acerca de esta cuestión, sobre la que volveremos más adelante.
Actividad 21:
El dueño de un diario editado en la ciudad de Córdoba desea abrir una sucursal en
el interior de la provincia. Para ello desea determinar la cantidad diaria de
ejemplares a imprimir sobre la base del número promedio de ejemplares
vendidos. Conoce, por información obtenida de otros diarios del lugar, que la
desviación estándar de la cantidad de ejemplares vendidos es de 2,5.
a) ¿Cuántos días deberá muestrear si está dispuesto a correr un riesgo del 1%
de cometer un error de estimación de 2 o menos ejemplares?
b) ¿Cuántos días deberá analizar si aumenta el error de estimación a 5
ejemplares? ¿Y si lo baja a 1?
c) ¿Cuál será el tamaño de n (con el error del inc. a) si se aceptara un riesgo del
10%?
Analice los valores obtenidos en cada caso y explique las diferencias.
d) ¿Qué efecto tendría sobre el riesgo del inc. a) el tomar una muestra de 9
días?
Actividad 22:
El mantenimiento de cuentas de crédito puede resultar demasiado costoso si el
promedio de compra por cuenta es menor a un cierto nivel. El gerente de una
empresa quiere conocer la cantidad mensual comprada por los clientes que usan
crédito, con un error de no más de $ 25 y una confianza aproximada de 0,95.
¿Cuántas unidades debe seleccionar de su archivo de 4000 cuentas, si sabe
además que la desviación estándar de las cuentas de crédito es de $ 75? ¿Porqué
los valores de
n0
y n son prácticamente iguales?
Si se trata de estimar una proporción, el mismo razonamiento conduce a la
fórmula:
n=
14/
z 2 p (1 − p )
e2
(10)
Imagine que usted necesita tomar una muestra de recién nacidos para estimar el peso promedio, y no conoce la varianza poblacional. Se conoce que su distribución es normal, cualquier
pediatra puede decirle cuál es el peso mínimo y máximo con que podrá encontrarse. Ese
rango, dividido por 6, será una buena aproximación al desvío estándar para usarlo en la
fórmula (9).
37
Cátedra I Estadística II
Autor I Hebe Goldenhersch
dado que se trata de una población dicotómica, en la que se desea estimar la
proporción de éxitos mediante una muestra.
Nuevamente surge el problema de tener que colocar en la fórmula un valor de p que
naturalmente se desconoce, puesto que es el parámetro que se desea estimar. En
este caso, puede observarse que si p = q = 0,5, el producto p(1-p) alcanza su
valor máximo (0,25) y éste es el que debe colocarse en la fórmula si no hay ningún
conocimiento acerca del posible valor de p15/.
(revise cuánto es el producto p(1-p) para valores alternativos de p, tales como 0,10,
0,20, 0,40, 0,60, etc).
Tenga en cuenta la naturaleza de la variable dicotómica, cuando deba precisar el error
máximo (e), en este caso no se trata de $, ni kg., sino de “proporción”, y el error
también se expresa como una proporción.
Veamos un ejemplo
Se quiere conocer de qué tamaño debe tomarse una muestra si en una población
muy grande se desea estimar la proporción de personas adultas que no han
completado la educación media.
1) No se tiene ninguna información acerca de esa posible proporción, se usará por
lo tanto una p = 0,50.
2) Se desea un nivel de confianza en la estimación del 95%, por lo tanto,
z = 1,96 (en muestreo suele redondearse a 2).
3) Se pretende que el error no supere a 0,05 (es decir, que la estimación resulte
en un valor de p estimado más menos 0,05).
Aplicando la fórmula (10):
2 .0, 5(1 − 0, 5)
2
n=
0, 05
2
= 400
Luego, será necesario tomar una muestra no menor a 400 casos para satisfacer las
exigencias planteadas.
Es conveniente realizar algunas reflexiones: este tamaño de muestra puede parecer
excesivo. Pero de este orden son las muestras necesarias cuando se quieren estimar
proporciones. No ocurre lo mismo cuando se desean estimar medias de poblaciones
para variables cuantitativas, que pueden tener varianzas pequeñas (como suele ocurrir
en biología o ciencias naturales); en esos casos, sobre todo si se trata de poblaciones
normales, a veces se puede trabajar con muestras pequeñas; pero si se trata de
estimar proporciones, las muestras siempre son de un tamaño considerable (para
estimar intención de voto, para estimar proporción de personas que acuerdan con
ciertos productos, o con ciertas medidas de política).
Nuevamente llamamos la atención acerca de la ausencia de N (tamaño de la
población) en la fórmula de cálculo... volveremos sobre esta cuestión.
Si existieran elementos de juicios para saber algo acerca de p, como por ejemplo si se
trata de estimar la proporción de desempleados en una comunidad donde se conoce
que ésta con seguridad no supera el 0,20, se colocará 0,20 en lugar de p y 0,80 para
1-p, así la muestra resultará menor que si se coloca 0,50.
15/
Sugerimos realizar el siguiente ejercicio: ¿cuál es el valor de p que hace máximo el producto
p.(1-p)? Busque ese valor aplicando lo que conoce de Matemática II acerca de maximizar
funciones.
38
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Actividad 23:
Se quiere estimar la incidencia de la hipertensión arterial en el embarazo.
¿Cuántas embarazadas habrá que observar para estimar (con una confianza del
95%) dicha incidencia con un error del 2% en los siguientes casos?:
a) Sabiendo que en un sondeo previo se ha observado un 9% de hipertensas.
b) Sin ninguna información previa.
Explique la diferencia entre ambos resultados.
Actividad 24:
La organización Apyme (que aglutina a las pequeñas y medianas empresas)
necesita realizar un estudio sobre la proporción de PyMEs exportadoras que han
sido beneficiadas con la devaluación del peso argentino. El Ministerio de la
Producción estima que el 65% de ellas han aumentado su nivel de ingresos por
esta razón. ¿Cuántas empresas deberá consultar esta organización si desea
realizar una estimación precisa de dicho porcentaje?, definiendo un error del
3% y tomando dos niveles de confianza:
a) 95,45%.
b) 99,73%.
Explique el efecto que tuvo sobre el tamaño de la muestra el cambio en el nivel de
confianza.
Actividad 25:
Para conocer si hubo un cambio con respecto al Censo poblacional de 1991 se
desea obtener una estimación para el año 2001 del número promedio de
personas que residen en la misma vivienda. En el país hay un total de
6.500.000 viviendas. En 1991 había un promedio de 3,15 personas por
vivienda y la varianza del número de personas por vivienda era de 0,5.
¿Cuántas viviendas se deben seleccionar para estar 95% seguros de que en el
año 2001 el número promedio de personas por vivienda está a una distancia no
mayor de 0,1 unidades de la media poblacional?
Actividad 26:
Se tiene previsto realizar una consulta popular a fin de conocer la opinión respecto
de la anticipación de las elecciones. ¿A cuántos votantes se deberá entrevistar en
un sondeo previo si se desea cometer un error no superior al 10% y depositar una
confianza del 0,95 en las conclusiones?
7.2. Error, riesgo y tamaño de la muestra
En las fórmulas planteadas para determinar el tamaño muestral:
n=
z 2 .σ 2
e2
y n=
z 2 . p (1 − p )
e2
puede observarse que el tamaño muestral depende de z, de la varianza y del error
máximo aceptable. Es conveniente reflexionar acerca de estos elementos:
•
z, valor extraído de la tabla de la distribución normal, determina la “confianza” de
las estimaciones que se realizarán (1- α ), y por lo tanto el “riesgo” α de
equivocarse al afirmar que cierto intervalo contiene al valor del parámetro;
•
la varianza, ( σ o p(1-p) ), indica una característica de la población, con respecto a
•
2
la variable de interés, si hay mayor o menor dispersión en la población, ello incide
en el tamaño muestral y
e, es el error máximo aceptable, medido en términos de la variable en cuestión si
es cuantitativa, o en términos de proporción si es dicotómica.
39
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Si en las fórmulas planteadas se despeja e, se observará que el error máximo depende
del riesgo aceptado, de la varianza y del tamaño de la muestra. El cociente entre la
varianza y el tamaño de la muestra, se conoce también como el cuadrado del “error
estándar” del estimador:
σ
p.(1 − p )
2
o
n
n
¿Usted podría explicar por qué a las raíces cuadradas de estas varianzas de los
estimadores (
σ
p.(1 − p )
o
) se las llama “errores estándar de estima-
n
n
ción”?
Actividad 27:
Suponga que un investigador desea realizar un estudio sobre el gasto de las
familias en la ciudad de Córdoba. Como no cuenta con información referida a esa
variable utilizará como desviación estándar muestral la referida al ingreso familiar,
obtenida en la Encuesta Permanente de Hogares, y que es s = $ 28,07.
a)
Encontrar el tamaño de muestra adecuado si el investigador indica que el
máximo error muestral no debe ser mayor que $ 2 por arriba o debajo de la
verdadera media del gasto, y toma dos niveles de confianza:
1) 95,45%.
2) 99,73%.
b) Indicar cuál es el valor del riesgo si se toman muestras de tamaño:
1) 500.
2) 2000.
e) ¿Cuál sería el error si el nivel de confianza es de 0,9545 y el tamaño de la
muestra es de 500 personas ?
7.3. Determinación del tamaño de la muestra teniendo en cuenta el error
relativo
Determinar el máximo error para una estimación en forma absoluta, puede constituir
un serio inconveniente, especialmente cuando se desconoce la magnitud aproximada
de los parámetros a estimar, sean estos medias o proporciones. Si en cambio, el error
se expresa en forma relativa, como por ejemplo: un 10% de la media, o un 5% de la
verdadera proporción, ese inconveniente sería superado, y se podría mantener un
error máximo acotado según las necesidades. No obstante, aparecen (como de
costumbre) otros inconvenientes a la hora de aplicar estas fórmulas. Simbolizando con
ε la proporción del parámetro deseada como error máximo, resulta:
e = ε .µ
o
e = ε.p
por lo tanto:
n=
Y recordando que
σ µ
z 2σ 2
ε 2 .µ 2
o
n=
z 2 p (1 − p )
ε 2 . p2
es el coeficiente de variación de la variable en cuestión (CV),
resulta:
n=
z 2 (CV ) 2
ε 2.
o
40
n=
z 2 (1 − p )
ε 2.p
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Estas fórmulas son adecuadas para calcular el tamaño de la muestra, cuando se
conoce el coeficiente de variación, si se trata de una variable cuantitativa, o se tiene
alguna idea del valor de p si es dicotómica, recordando que ahora se trata de un “error
relativo”. Así por ejemplo, si ε = 0,10, significa que el máximo error aceptable es un
10% del valor del parámetro, sea éste una media o una proporción.
En el caso de la media, suele resultar una ventaja el uso del coeficiente de
variación en lugar de la varianza, ya que puede ser más estable, y en ese caso sería
posible utilizar confiablemente valores obtenidos con anterioridad para ese coeficiente,
o referidos a otras variables con un comportamiento similar.
Cuando se trata de una población finita, y se extrae la muestra sin reemplazo, es
necesario aplicar el factor de corrección para las varianzas que intervienen en las
fórmulas (9) ó (10). (Recordar de Estadística I esta corrección para muestreo sin
reemplazo).
En ese caso resulta (para la fórmula (9)):
z .σ
2
n=
e
2
2
.
N −n
N −1
como n aparece en ambos miembros, es necesario despejar. Llamando
n∞
al
resultado de calcular el tamaño de muestra con reemplazo:
n = n∞ .
N −n
N −1
y despejando
n=
n ∞ .N
(N-1)+n ∞
Verifique que al despejar se obtiene el resultado indicado.
Para el caso de la proporción, llamando
n∞
al resultado de (10), resulta exactamente
la misma fórmula.
El tamaño de muestra así calculado, resulta algo menor al del muestreo con remeplazo. Pero para que esa reducción tenga un efecto interesante, es posible advertir,
analizando la fórmula, que n, tamaño de la muestra, debe ser importante (“grande”),
comparado con N, tamaño de la población. La evidencia empírica indica que debe
aplicarse la fórmula corregida, sólo cuando el tamaño de la muestra calculado,
resulta superior al 5% del tamaño de la población, de lo contrario no es necesaria la corrección ya que la reducción en el costo (por menor tamaño muestral) será
imperceptible.
A continuación le proponemos una serie de actividades a resolver:
Actividad 28:
Una compañía de transporte local de pasajeros piensa establecer una línea desde
un determinado barrio hasta el centro de la ciudad. Dicha empresa quiere estimar
la proporción de usuarios que utilizarían esta nueva ruta, con una confianza del
95% y un error máximo de ± 0,02. ¿Cuántas personas, sobre una población de
8.000 potenciales usuarios, debería entrevistar a fin de tomar la decisión de imple-
41
Cátedra I Estadística II
Autor I Hebe Goldenhersch
mentar el nuevo servicio? ¿Por qué los valores de
n∞ y n son diferentes?
Actividad 29:
Una compañía de televisión por cable, que cuenta con 5000 suscriptores en una
determinada ciudad, querría estimar la proporción de los mismos que comprarían
su revista mensual con la programación. Dicha empresa querría tener un 95% de
confianza de que su estimación es correcta, con aproximación de ± 0,05. La
experiencia previa en otras ciudades indica que cerca del 30% de los suscriptores
compran la revista. ¿Qué tamaño de muestra es el adecuado a estos requerimientos si el muestreo se realiza sin reposición?
Actividad 30:
Se desea estimar la resistencia media a la tracción de una remesa de 1000
alambres de acero. Se conoce de estudios anteriores que la desviación estándar
de la resistencia a la tracción es de aproximadamente 9,07 kg. ¿Qué cantidad
de alambres de acero se deberán muestrear de la remesa, sin reposición, si se
desea trabajar con una confianza de 0,95 de cometer un error de muestreo de
3 kg. o menos?
Actividades Complementarias
Actividad 31:
Para llegar a una negociación salarial adecuada en un determinado sindicato se
requiere una estimación precisa del salario actual de los empleados sindicalizados.
Un agente laboral tomó una muestra de n = 60 empleados sindicalizados y en ella
se encontró una media del salario quincenal de $ 247,45. Se sabe, de estudios
anteriores, que la desviación estándar poblacional es de $ 21,60. Determinar un
intervalo de confianza del 95% para el salario quincenal promedio de todos los
empleados sindicalizados.
Actividad 32:
Un laboratorio muy importante está probando la reacción de una nueva droga
para acelerar el crecimiento. Se aplicó la misma a una muestra aleatoria de 120
animales de laboratorio, arrojando un crecimiento promedio de 10 cm. y una
varianza muestral de 2,56 cm2.
Se pide:
a) Encontrar un intervalo de confianza del 95% para µ.
b) ¿Qué tan grande debería tomarse la muestra si se desea que la media
muestral no difiera de la media poblacional en más de 1 cm.?
Actividad 33:
En una semana de trabajo determinada se elige al azar una muestra de 300
empleados de una empresa manufacturera. Los trabajadores realizan una labor
a destajo y se encuentra que el promedio de pago por pieza trabajada es de
x = $ 18 con una desviación estándar de s = $ 1,4. Estimar, con un nivel del
95%, un intervalo de confianza para el pago promedio a destajo de todos los
empleados de la empresa.
Actividad 34:
Un supervisor del proceso de empacado de café en sobres tomó una muestra
aleatoria de 12 en la misma planta empacadora. El peso neto de dichos sobres de
café fue el siguiente:
42
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Gramos por sobre
15.7
15.8
15.9
16
16.1
16.2
Cantidad de sobres
1
2
2
3
3
1
Suponiendo que el peso del café empacado tiene distribución normal, estimar el
peso promedio por sobre utilizando un nivel de confianza de 0,95.
Actividad 35:
El Dpto. de Marketing de un supermercado recopila datos de una muestra
aleatoria de 100 clientes, seleccionados sin reposición de un conjunto de 400
clientes, titulares de una determinada tarjeta de crédito. Las 100 personas
gastaron un promedio de $ 98,28 en el supermercado, con una desviación
estándar de $ 26,40. Utilizando un nivel de confianza del 95% se pide estimar:
a) el monto promedio de las compras para los 400 clientes
b) el monto total, en pesos, para las compras realizadas por los 400 clientes.
Actividad 36:
En una muestra aleatoria de 15 alumnos del 5º año de un colegio secundario se
encontró que 5 de ellos tenían decidida la carrera universitaria a seguir.
Estimar la proporción de estudiantes secundarios que tienen decidido qué
carrera seguir, a un nivel de 0,99.
Actividad 37:
Un analista financiero desea estimar el número promedio de sucursales de bancos
extranjeros que se encuentran en el país. Conoce, por estudios muestrales
previos, que la varianza poblacional es aproximadamente igual a 500. Sus
requerimientos son:
- máximo error muestral permitido: 3
- nivel de confianza: 95,45%.
¿Cuántos bancos se deberán muestrear, sin reposición, para satisfacer estos
requerimientos?
Se estima que la población de bancos extranjeros radicados en el país es de
aproximadamente 60.
Actividad 38:
El dueño de una radio quiere conocer la proporción de gente que gusta de los
programas deportivos. A cuántas personas deberá encuestar si:
a) - el error muestral no debe ser mayor a un 2%
- el nivel de confianza es de 95%
- la proporción de gente que gusta de estos programas es aproximadamente
de 0,60
b) no se conoce nada acerca de la proporción de gente que gusta de este tipo de
programas.
Actividad 39:
a) ¿Cuántos intervalos de confianza se pueden construir para estimar µ?
b) ¿Y para estimar P?
c) ¿Todos contendrán el valor del parámetro?
d) Se toma una muestra particular de tamaño n y se construye el intervalo de
confianza ¿contendrá este intervalo el verdadero valor del parámetro?
43
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Actividad 40:
a) ¿Para qué sirve conocer el error estándar de un estimador?
b) ¿Es lo mismo que el error de estimación?
Indique las fórmulas que conoce para cada caso.
Actividad 41:
Responda las siguientes aseveraciones con Verdadero o Falso, justificando en
cada caso:
1. Un intervalo de confianza de nivel 99% para la media siempre contiene el
valor desconocido de la media poblacional.
2. Si el tamaño de la muestra y la varianza poblacional permanecen
constantes, y se disminuye el nivel de confianza del intervalo, entonces su
amplitud aumenta.
3. Si el tamaño de la muestra y el nivel de confianza son fijos, y la variabilidad
poblacional es mayor a la supuesta originalmente, entonces el nuevo
intervalo de confianza que se obtiene será más amplio.
4. Mientras más observaciones se toman, menor amplitud tendrán los
intervalos que se construyan.
5. Si se tiene una muestra grande, se puede usar la distribución normal para
plantear intervalos de confianza.
6. Un intervalo de confianza de (1-α) para un parámetro está contenido en el
correspondiente intervalo de confianza de (1-α/); siendo α > α/.
7. Si disminuye el nivel de confianza, disminuye la amplitud del intervalo y
disminuye también el error estándar del estimador.
Actividad 42:
Una pequeña industria dedicada a la fabricación de pilas produce 345 unidades
diarias. Ante el reclamo de sus clientes en el sentido de que las mismas duran
menos de 1000 hs. este fabricante pretende mostrar una estimación de la
verdadera duración promedio de sus pilas. Esta industria conoce que la
desviación típica poblacional es de 120 hs.
La información disponible es:
Estadística descriptiva
Resumen
n
Media
Var(n-1)
E.E.
Mín
Máx
Mediana
Q1
Q3
Pilas
81
1203,38
12780,14
12,56
905
1523
1201
1121
1267
a) Indique cuál sería la estimación al nivel del 90%.
b) Si el error máximo tolerado fuera de 47,04 hs., ¿qué cantidad de pilas
debería haber seleccionado?
Actividad 43:
Se tomó una muestra de 61 empresas exportadoras de la industria alimenticia
que arrojó los siguientes volúmenes de exportación anual:
44
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Exportaciones
(miles de $)
10- 50
50- 90
90-130
130-170
170-250
Cantidad de
empresas
9
19
21
7
5
Con un 90% de confianza estime:
a) la exportación media anual de las empresas de esta rama industrial.
b) el porcentaje de empresas que no han alcanzado los 90 mil pesos de
exportación anual.
Actividad 44:
El Dpto. de Marketing de un supermercado recopila datos de una muestra
aleatoria de 100 clientes, seleccionados sin reposición de un conjunto de 400
titulares de una determinada tarjeta de crédito. Las 100 personas gastaron un
promedio de $ 98,28 en el supermercado, con una desviación estándar de $
26,40. Utilizando un nivel de confianza del 95% ¿puede estimar el monto total, en
pesos, para las compras realizadas por los 400 clientes?
Actividad 45:
Una editorial que lanza al mercado un nuevo periódico desea saber qué cantidad
diaria aproximada debe imprimir. Para ello releva información, durante tres
semanas, de la demanda diaria de ejemplares de otro diario local.
Demanda diaria
2451
2175
2565
2619
2278
2681
2679
2369
2610
2409
2209
2015
2404
2668
2762
2315
2912
2732
2809
2411
2658
Cuantiles observados(demanda diaria)
¿Qué cantidad diaria a imprimir le sugiere a esta editorial? Use (1-α) = 0,99.
Q-Q plot
2951,63
n= 21 r= 0,987 (demanda diaria)
2717,48
2483,32
2249,16
2015,00
2015,00 2249,16 2483,32 2717,48 2951,63
Cuantiles de una Normal(2511,54382)
demanda diaria
45
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Si en lugar de tratarse de algún parámetro desconocido de una población se trata de
dos poblaciones (la misma variable), y con el objeto de considerar las diferencias
que pudieran existir entre ambas, se desea comparar sus parámetros, surge un
problema diferente, que es el de estimar funciones en que intervienen parámetros
de las dos poblaciones.
Podría plantearse como ejemplo estimar la diferencia entre las medias de ventas
de dos sucursales de una empresa, o entre las varianzas del diámetro de las piezas
producidas en dos máquinas diferentes, o entre los porcentajes de población
económicamente activa existentes en dos ciudades capitales de provincia...
9.1. Diferencia de medias, muestras independientes
Se trata de estimar la diferencia existente entre µ1 y µ 2 , medias de dos poblaciones, a
partir de dos muestras independientes; esto es tomando una muestra de cada
población; se plantea:
a) El estimador de la diferencia de medias poblacionales, es la diferencia entre las
medias muestrales: X 1
− X2
b) La esperanza de la diferencia, es igual a la diferencia de las esperanzas, por lo
tanto la esperanza del estimador, es µ1
− µ 2 ; la varianza del estimador, por ser las
muestras independientes, es igual a la suma de las varianzas (recordar
2
propiedades de la varianza), luego: σ X
1−X2
= σ X2
2
1
+σX
2
=
σ 12
n1
+
σ 22
n2
Se plantean entonces algunas alternativas para determinar el estadístico adecuado.
9.1.1. Varianzas poblacionales conocidas
Siendo las poblaciones normales o las muestras suficientemente grandes como para
aplicar el Teorema Central del Límite (se considera “suficiente” si cada muestra es
superior a 30), entonces el estadístico:
( X 1 − X 2 ) − ( µ1 − µ 2 )
σ 12 n1 + σ 22 n2
simbolizando con σ X
1
−X2
~ N (0,1)
(11)
(error estándar de la diferencia de medias) al denominador,
considerando la distribución normal, y despejando el parámetro a estimar, resulta:
P (( X 1 − X 2 ) − z1−α 2 .σ X − X < ( µ1 − µ 2 ) < ( X 1 − X 2 ) + z1−α 2 .σ X − X ) = 1 − α
1
2
1
2
que es la fórmula adecuada para estimar un intervalo de confianza para la diferencia
de medias, cuando se conocen las varianzas poblacionales.
46
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Actividad 46:
El gerente general de una empresa internacional ha estado examinando la cuenta
de gastos del personal de los departamentos de Producción y Comercialización,
conociendo por datos obtenidos de años anteriores que la desviación estándar
para cada departamento es σ1 = 10 (departamento de Producción) y σ2 = 7
(departamento de Comercialización). Se tomó una muestra aleatoria de 5
empleados del departamento de Producción y 9 empleados de Comercialización
con los siguientes resultados:
x1
= 150 y
x2 =
200. Determinar, mediante la
construcción de un intervalo de confianza para la diferencia de medias, si hay
diferencia significativa en los gastos promedio del personal de ambos
departamentos con un nivel del 90% si se conoce además que dichos gastos se
distribuyen en forma aproximadamente normal.
9.1.2. Varianzas poblacionales desconocidas
En este caso, es necesario buscar un estadístico adecuado que no contenga las
varianzas poblacionales. Como en el caso de la estimación por intervalos de la media,
cuando se desconoce la varianza, el estadístico está asociado a la distribución t. Pero
ahora es necesario algún supuesto adicional bastante restrictivo, además del ya
conocido de distribución normal de la variable en cada una de las poblaciones.
Si esto se cumple, el estadístico (11), ya vimos que tiene distribución normal, y el
estadístico:
( n1 − 1) S1
( n2 − 1) S 2
2
2
+
σ1
2
σ2
2
~ χ n2 + n − 2 (12)
1
2
por ser suma de dos estadísticos con distribuciones χ n −1
2
1
χ
sugiere revisar en Estadística I la distribución
2
y χ n2 −1 respectivamente. Se
2
.
El cociente entre el estadístico (11) y la raíz cuadrada de (12) dividido por sus grados
de libertad, tiene una distribución t de Student, con los mismos grados de libertad de
la
χ 2 (es
decir n1 + n2 − 2 ). Pero en ese cociente no es posible eliminar las σ
2
desconocidas. Ahora bien, si se agrega un nuevo supuesto: las varianzas de ambas
poblaciones, si bien desconocidas, son iguales, entonces el cociente de los
estadísticos resulta (al reemplazar σ 1 y σ 2 por σ - sin subíndice porque son iguales):
2
2
2
( X 1 − X 2 ) − ( µ1 − µ 2 )
σ
( n1 − 1) S1
2
σ
Simplificando se eliminan las
σ
n1 + σ
2
( n2 − 1) S 2
n2
~ tn1 + n2 − 2
2
+
2
2
σ
/( n
1
2
+ n2 − 2)
2
y resulta:
( X 1 − X 2 ) − ( µ1 − µ 2 )
( n1 − 1) S + ( n2 − 1) S
2
1
2
2
n1 + n2 − 2
.
n1 + n2
~ tn + n − 2
1
2
(13)
n1 .n2
Usted puede observar que el denominador (error estándar del estimador de la
diferencia de medias) es la raíz cuadrada de la media ponderada de ambas varianzas
muestrales; por ello varios paquetes estadísticos llaman a este caso, el de las
“varianzas combinadas” o “pooled” en inglés.
47
Cátedra I Estadística II
Autor I Hebe Goldenhersch
En adelante llamaremos S X
1− X2
a este denominador (error estándar combinado de la
diferencia de medias).
El supuesto de las varianzas poblacionales iguales debe ser probado mediante los
métodos que se estudian en el capitulo referido a la prueba de hipótesis, o mediante
un intervalo de confianza para el cociente de varianzas, tal como se trata en el punto
siguiente.
A partir de esa prueba, si se concluye que no hay evidencias para sospechar que las
varianzas son diferentes, se aplica el estadístico (13); si las hay, esto es si las
varianzas poblacionales no pueden considerarse iguales, existe un estadístico desarrollado por Satterthwaite, en el cual se consideran las varianzas de ambas muestras
"separadas" (como se hace con las poblacionales cuando éstas son conocidas),ya que
no es correcto combinarlas; la distribución es también t de Student pero es necesario
recalcular los grados de libertad, los cuales resultan menores que en el estadístico
(13). Dicho cálculo se realiza de la siguiente forma (los grados de libertad de la t son
en ese caso, la parte entera de v):
2
S1
(
v=
2
+
n1
2
S2
)
n2
2
2
S1
( )
S2
( )
2
n1
n1 − 1
+
2
n2
n2 − 1
El estadístico es entonces:
( X 1 − X 2 ) − ( µ1 − µ 2 )
S
n1 + S 2 n2
2
2
1
~ tv
(14)
Si las varianzas poblacionales son iguales, el intervalo de confianza resulta:
P (( X 1 − X 2 ) − t n + n
1
2
− 2(1−α 2)
.S X − X < ( µ
1
2
1
− µ 2 ) < ( X 1 − X 2 ) + tn + n
1
2
− 2(1−α 2)
.S X − X ) = 1 − α
1
2
Si las varianzas poblacionales no son iguales, tenemos:
P (( X − X ) − t v (1−α
1
2
2)
S
2
1
n +S
1
2
2
n < ( µ1 − µ 2 ) < ( X − X ) + t v (1−α
2
1
2
2)
S
2
1
n +S
1
2
2
n = 1−α
2
En este último caso, observe que son v los grados de libertad. Como de costumbre, si
v es suficientemente grande, se utilizan los valores de la distribución normal.
Actividad 47:
Una empresa de nuestra ciudad dedicada a la fabricación de jabón en polvo posee
una sucursal en el interior de la provincia. El gerente de fabricación piensa que la
producción media diaria (medida en cantidad de paquetes) de la sucursal es
mayor que la de la casa matriz. Para saber si esto es así, se toman muestras
aleatorias con los siguientes resultados:
(La interpretación correcta de la segunda parte de la salida de computadora:
“Prueba F…”. Se estudiará en el Capítulo III del programa, por ahora usted puede
suponer que las varianzas poblacionales son iguales).
48
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Paquetes casa matriz
521
535
567
527
564
561
518
546
506
Paquetes sucursal
539
541
531
576
554
569
529
556
549
Cuantiles observados(paquetes)
sucursal
576,00
n= 9 r= 0,983 (paquetes)
563,30
550,59
537,89
525,18
525,18
537,89
550,59
563,30
576,00
Cuantiles de una Normal(549,33,261,25)
paquetes
Cuantiles observados(paquetes)
casa matriz
571,54
n= 9 r= 0,974 (paquetes)
554,94
538,33
521,73
505,12
505,12
521,73
538,33
554,94
571,54
Cuantiles de una Normal(538,33,494)
paquetes
Prueba F para igualdad de varianzas
Variable
paquetes
n(1)
9
n(2)
9
Var(1)
494,00
Var(2)
261,25
F
1,89
p
0,3863
Con un nivel del 99%, opine sobre lo que piensa el gerente de esta empresa.
Actividad 48:
Los directores de una empresa dedicada a la fabricación de bolígrafos deben
decidir la implementación o no de un nuevo proceso de fabricación de lapiceras. Si
bien el nuevo proceso implica una disminución sustancial en los costos, quieren
saber si la duración de la carga de tinta es aproximadamente la misma en ambos
procesos. Para ello, el departamento de estadística de la empresa tomó una mues-
49
Cátedra I Estadística II
Autor I Hebe Goldenhersch
tra de bolígrafos fabricados por cada uno de los procesos, obteniendo los
siguientes resultados:
Proceso antiguo
n1 = 200
Σxi = 11460 hs.
s12 = 9
Proceso nuevo
n2 = 150
Σyi = 8565 hs.
s22 = 16
A partir de la construcción del intervalo de confianza que corresponda, ¿puede
contestar si se debe implementar o no el nuevo proceso de producción, a un nivel
del 95%?
¿Qué supuestos deberían corroborarse antes de construir dicho intervalo?
Actividad 49:
Con la salida que se muestra a continuación, ¿puede decir si existe diferencia
significativa en la duración (en km.) de dos marcas de neumáticos? Si construyera
usted el intervalo informado, ¿obtendría los mismos límites? (La interpretación
correcta de la segunda parte de la salida de computadora: “Prueba F…”. Se
estudiará en el Capítulo III del programa, por ahora usted puede suponer que las
varianzas poblacionales son iguales).
Intervalo T para muestras Independientes
Clasif.
marca
Variable
vida útil
n(1)
10
n(2)
8
media(1)
4651,53
media(2)
4040,13
LI(90%)
436,74
LS(90%)
786,06
F
1,52
p
0,5942
Prueba F para igualdad de varianzas
n(1)
10
n(2)
8
Var(1)
52315,61
Var(2)
34411,52
m a rc a = 1
5005,28
C u an tiles o bs ervad os (vid a útil)
Variable
vida útil
n= 10 r= 0,984 (v ida útil)
4828,40
4651,52
4474,65
4297,77
4297,77 4474,65 4651,52 4828,40 5005,28
C u a n tile s d e u n a N o rm a l(4 6 5 1 ,5 ,5 2 3 1 6 )
50
Cátedra I Estadística II
Autor I Hebe Goldenhersch
m a rc a = 2
C uantiles ob s ervad os (vid a útil)
4326,73
n= 8 r= 0,993 ( v ida útil)
4177,39
4028,06
3878,72
3729,39
3729,39 3878,72 4028,06 4177,39 4326,73
C u a n tile s d e u n a N o rm a l(4 0 4 0 ,1 ,3 4 4 1 2 )
9.2. Diferencia de medias. Muestras dependientes (observaciones apareadas)
Cuando se trata de construir un intervalo de confianza para la diferencia de medias
poblacionales, pero se parte de un par de muestras dependientes, no puede utilizarse
ninguno de los estadísticos planteados en los puntos anteriores, ya que todos se basan
en las propiedades de la varianza para variables independientes.
Algunos ejemplos de situaciones en que no hay muestras independientes aclararán
el concepto. Un caso frecuente es aquél en que ambas muestras corresponden a
las mismas observaciones en distintos momentos del tiempo: por ejemplo, se trata
de construir un intervalo para la diferencia de medias de tensión arterial antes y
después de un tratamiento, para una muestra de pacientes hipertensos (hay una
diferencia de medias “antes” y “después”, pero se tomó una sola muestra y se
realizaron a los mismos individuos dos mediciones; o se trata de analizar la
diferencia entre el rendimiento promedio de un grupo de operarios trabajando en
un turno matutino y el mismo grupo trabajando en turno vespertino; o la
diferencia en los montos promedio de ventas de una muestra de vendedores antes
y después de haber realizado un curso de capacitación para ventas… En estos
casos, las diferencias no constituyen observaciones de muestras independientes
puesto que se trata de la misma muestra observada en dos oportunidades; el valor
de la variable no depende sólo del momento en que se mide, sino también de la
observación de que se trata16/.
Para situaciones como las referidas, es conveniente, en lugar de trabajar con las
variables X 1 y
X 2 , definir una nueva variable que sea igual a la diferencia entre
ambas:
D = X1
16/
− X2 ,
siendo cada observación d i = x1i
− x2 i
Hay otras situaciones de muestras dependientes, las que siempre tienen en común el hecho
que no hay dos muestras seleccionadas independientemente al azar, sino que la elección
aleatoria de una de ellas determina la de la segunda. Por ejemplo, se desea construir un
intervalo de confianza para la diferencia entre las medias de temperatura de un grupo de
pacientes que sufren de cierta afección y los que no la sufren; se toma una muestra de
pacientes con la afección, y luego a cada uno de ellos se “aparea” una persona con
características lo más similares posibles de edad, sexo, peso, etc. pero en los que esa afección
está ausente. Sólo hay una muestra elegida al azar, la otra se construye buscando uno a uno
los individuos adecuados.
51
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Muestra 1
Muestra 2
d
x11
x21
d1
x12
x22
d2
…..
….
…
x1n
x2n
dn
De esta manera, se calculan la media y varianza muestrales de la nueva variable D y
se utiliza un estadístico similar al necesario para construir un intervalo de confianza
para la media de una variable (en este caso, la variable D). Como se trabaja siempre
con la varianza muestral, siendo la varianza poblacional desconocida, corresponde
utilizar el estadístico con distribución t de Student y se necesita el supuesto de
poblaciones normales (ver punto 6.2.):
Media muestral:
d =
∑ di
n
Media poblacional:
∆
Varianza estimada muestral:
2
Sd
=
∑ d i2 − nd 2
17/
n −1
El estadístico adecuado es entonces:
d −∆
~ tn −1
Sd n
Y el intervalo de confianza para la diferencia poblacional
LIC = d − tn −1(1−α
2)
Sd
n
∆ resulta:
LSC = d + tn −1(1−α
2)
Sd
n
Actividad 50:
Un fabricante desea comparar el desgaste de dos distintos tipos de neumáticos A
y B. Para realizar la comparación se montan en las ruedas traseras de cada uno
de 10 automóviles un neumático del tipo A y uno del tipo B. Éstos se usan por
una distancia preestablecida y se registra la cantidad desgastada de cada
neumático. Los datos obtenidos fueron:
Automóvil
1
2
3
4
5
6
7
8
9
10
17/
Neumático A
10,60
9,80
12,3
9,7
8,8
12,35
10,55
8,93
9,24
10,00
Neumático B
10,14
9,52
11,98
9,3
8,48
12,01
10,09
8,63
9,00
9,50
Se trata de una fórmula de cálculo, usted puede verificar que se obtiene a partir de la definición de varianza muestral corregida.
52
Cátedra I Estadística II
Autor I Hebe Goldenhersch
C ua n tiles o b s e rva do s (d if.ne u m áticos A y B)
Observando los datos de la muestra se puede ver que los valores de la primera
columna son mayores a los de la segunda. ¿Se puede decir que esto es así en la
población? En caso afirmativo, ¿en cuánto más se desgastan los neumáticos A en
comparación con los neumáticos B? Trabaje con una confianza de 0,95.
Q-Q plot
0,50
n= 10 r= 0,968 (dif .neumáticos A y B)
0,43
0,36
0,30
0,23
0,23
0,30
0,36
0,43
0,50
C uantiles de una Norm al(0,36294,0,0075438)
dif . neumáticos A y B
Actividad 51:
Para comparar la efectividad de un programa de seguridad en el trabajo la
Cámara de Industriales Metalúrgicos observó, en 12 plantas industriales, el
número de accidentes por año antes y después de dicho programa.
Con los datos de la salida que se muestran a continuación indique si la Cámara
puede recomendar la implementación de dicho programa.
Intervalos de confianza (muestras apareadas)
Obs(2)
después
N
12
media(dif)
3,83
DE(dif)
3,59
LI(90%)
1,97
Q-Q plot
10,00
C uantiles obs ervados
Obs(1)
antes
n= 12 r= 0,970 (dif erencia)
6,99
3,98
0,97
-2,03
-2,03
0,97
3,98
6,99
10,00
Cuantiles de una Norm al(3,8333,12,879)
dif erencia
53
LS(90%)
5,69
Cátedra I Estadística II
Autor I Hebe Goldenhersch
9.3. Diferencia de proporciones. Muestras independientes
Se trata de obtener el estadístico adecuado para construir intervalos de confianza para
una diferencia de proporciones, estamos hablando por lo tanto de dos poblaciones
dicotómicas. Sólo consideramos el caso de muestras independientes y suficientemente
grandes como para usar la aproximación normal (esto es, np y nq mayores que 5 para
cada una de las muestras).
Los estimadores de cada una de las proporciones poblacionales son las proporciones
muestrales, y por propiedades de esperanza y varianza de una diferencia de variables
aleatorias independientes, el estadístico es:
(pˆ 1 − pˆ 2 ) − ( p1 − p2 )
pˆ 1 (1 − pˆ 1 )
n1
+
pˆ 2 (1 − pˆ 2 )
~ N (0,1)
n2
Las proporciones estimadas en el denominador, utilizadas como estimadores de los
errores estándar de la proporción en cada muestra, se aplican por desconocimiento de
las poblacionales, produciéndose por este motivo un error adicional que, en general,
no es importante (ver punto 6.3.).
Simbolizando con
σˆ pˆ − pˆ
1
2
el denominador de la expresión anterior, el intervalo resulta:
LIC (pˆ1 − pˆ 2 ) − z1−α 2 .σˆ pˆ1 − pˆ 2
LSC = (pˆ1 − pˆ 2 ) + z1−α 2 .σˆ pˆ1 − pˆ 2
Actividad 52:
Al intentar medir la opinión de los padres respecto a un nuevo plan de estudios,
un supervisor escolar recopila muestras aleatorias de 100 padres de familia, en
cada una de las dos regiones más importantes incluidas en el sistema escolar. En
la primera región 70 padres de familia señalaron que están a favor del nuevo plan
de estudio; mientras que en la segunda región sólo 50 padres indicaron estar a
favor. ¿Existe diferencia en la opinión de los padres en las dos áreas, a un nivel
del 95%?
Actividad 53:
En una fábrica de alfajores donde hay instaladas dos líneas de armado y
horneado, una muestra de n1 = 200 alfajores de la primera línea mostró 15
unidades desgranadas; mientras que una muestra de n2 = 100 alfajores de la
otra línea mostró 12 desgranados. Si compara ambas líneas, ¿qué puede concluir
a un nivel de confianza del 99%?
9.4. Intervalo de confianza para el cociente de varianzas. Poblaciones normales
Cuando se desea establecer un intervalo de confianza que compare las varianzas de
dos poblaciones, tomando muestras de forma independiente en cada una de ellas, hay
que tener en cuenta que para comparar varianzas existen estadísticos que contemplan
el cociente, en lugar de la diferencia (como ocurre para medias o proporciones). Si se
recuerda de Estadística I que el estadístico:
(n1 − 1) S12
( n1 − 1)σ 12
( n2 − 1) S 22
~ F( n1 −1,n2 −1)
( n2 − 1)σ 22
Tiene esta distribución por tratarse de un cociente entre dos
54
χ2
independientes,
Cátedra I Estadística II
Autor I Hebe Goldenhersch
divididas por sus grados de libertad.
Luego, simplificando, resulta el estadístico:
S12σ 22
S 22σ 12
~ F( n1 −1,n2 −1)
Al despejar el cociente de varianzas poblacionales, se obtiene el intervalo de confianza
(para el cociente
σ 12
):
σ 22
LIC =
S12
1
LSC =
S 22 F1−α 2
S12 1
S 22 Fα
2
Recuerde de Estadística I, cómo debe buscar el valor de F para una probabilidad de
cola izquierda, a fin de obtener el
Fα 2 .
Actividad 54:
Se intenta lanzar al mercado un nuevo tipo de plástico que se presume posee
menos variabilidad en la resistencia a la rotura que el que se produce
actualmente. Se tomaron dos muestras aleatorias, una de cada tipo de plástico, y
se los sometió a pruebas de resistencia, con los siguientes resultados:
Tipo I: 75 40 80 63 49
Tipo II: 47 72 69 59 65 73 50
Suponiendo que ambas poblaciones se distribuyen normalmente, determinar si
existe diferencia significativa, a un nivel del 99% para la variabilidad en la
resistencia a la rotura de ambos tipos de plástico.
Actividad 55:
En la industria de manufacturas metálicas la productividad, y consecuentemente
la utilidad, depende en gran medida de la calidad y uniformidad de las materias
primas. Suponga que se tienen bajo consideración dos fuentes principales de
materias primas, para las cuales el fabricante no está seguro acerca de su
respectiva uniformidad en el contenido de impurezas. Se toman 10 muestras de
100 kg. cada una de cada fuente y se determina la cantidad de impurezas en cada
muestra. Los resultados fueron:
Material A
Material B
y1 = 41,30
y2 =
39,60
s12 =
s22 =
7,85
18,75
¿Sugieren estos datos una diferencia significativa en la uniformidad en el
contenido de impurezas en los dos materiales, a un nivel de 0,90?
Suponga poblaciones normales.
9.5. Consideraciones generales para interpretar los intervalos de confianza
para diferencias de medias o proporciones y cocientes de varianzas
La interpretación de estos intervalos se relaciona íntimamente con las pruebas de
hipótesis para comparar medias, proporciones o varianzas de dos poblaciones, tema
que se estudia en el Capítulo III. En este Capítulo se trata de dar una interpretación
que deberá ser completada luego con aquellos conceptos.
55
Cátedra I Estadística II
Autor I Hebe Goldenhersch
Si se obtiene un intervalo de confianza para la diferencia de medias de dos poblaciones, llamando a y b a los límites inferior y superior del mismo, puede decirse, con una
confianza igual a 1 − α que:
a < µ1 − µ 2
<b.
Esto puede leerse como que, con una elevada confianza, puede esperarse que la
diferencia de medias esté comprendida entre a y b. Si a y b son ambos positivos,
significa que es muy probable que µ1 sea mayor que µ 2 ; si, por el contrario, ambos
límites son negativos, ello implica que es muy probable que µ1 sea menor que µ 2 (por
eso la diferencia negativa).
En cambio, si a es negativo y b es positivo, ello sugiere que la diferencia entre las
medias poblacionales puede ser tanto negativa como positiva, no pudiendo afirmar
nada respecto a cuál de las medias es mayor.
Es por este razonamiento que suele afirmarse, en cualquiera de los dos primeros casos
(ambos extremos de igual signo), que la diferencia observada entre las medias
muestrales es significativa, en el sentido que indica con alta probabilidad que una de
las medias poblacionales es mayor que la otra. Por el contrario, si los signos son
diferentes, se afirma que la diferencia entre las medias muestrales no es
significativa, en el sentido que no puede afirmarse, a partir de los resultados
muestrales, que alguna de las medias poblacionales supere a la otra.
Este mismo razonamiento se aplica para la diferencia de proporciones. Si en cambio,
se trata de un cociente de varianzas, el intervalo sería de la forma:
σ 12
a< 2 <by
σ2
en
este
caso,
la
existencia
de
diferencia
significativa
o
no
significativa entre las varianzas muestrales se determina según a y b sean ambos
menores que 1 (en ese caso la segunda varianza es menor que la primera), ambos
mayores que 1 (la segunda varianza es mayor que la primera). Pero si a es menor que
1 y b mayor que 1, entonces concluimos que no hay diferencia significativa entre las
varianzas muestrales, que permita concluir la existencia de una diferencia entre las
varianzas poblacionales.
Interpretar los resultados de los ejercicios anteriores sobre diferencias.
Ejercicio adicional
Finalizamos aquí el primer Capítulo, donde hemos aprendido a “estimar” parámetros
desconocidos de una población, y a comparar parámetros de dos poblaciones.
Sugerimos como actividad de cierre de este apartado revisar la forma en que se fueron
planteando los problemas; volver sobre las consignas dadas en cada caso, reconocer
datos y preguntas, para finalmente, reflexionar sobre la manera en que los ha
resuelto, el “tipo de razonamiento” seguido y los posibles obstáculos o dificultades que
se fueron presentando en este proceso. Sería interesante también que intente
“inventar” posibles problemas, desafiando de ese modo la identificación de situaciones
de la práctica profesional o la vida cotidiana en las que la estimación puede ser de
utilidad.
En el Capítulo III se retomará el tratamiento de los estadísticos aquí utilizados, pero
para encarar el otro aspecto fundamental de la Inferencia Estadística: la prueba o
contraste de hipótesis.
Antes de eso en el Capítulo II, estudiaremos cómo se toman las muestras para
realizar las estimaciones o las pruebas de hipótesis. ¿Por qué este orden? Porque
56
Cátedra I Estadística II
Autor I Hebe Goldenhersch
resultan muy importantes para definir el método de muestreo de los conceptos de
“error” y “precisión” de las estimaciones que hemos desarrollado en el presente
Capítulo.
57