TEMA 3 - Unidad de Ciencias de la Atmósfera
Anuncio
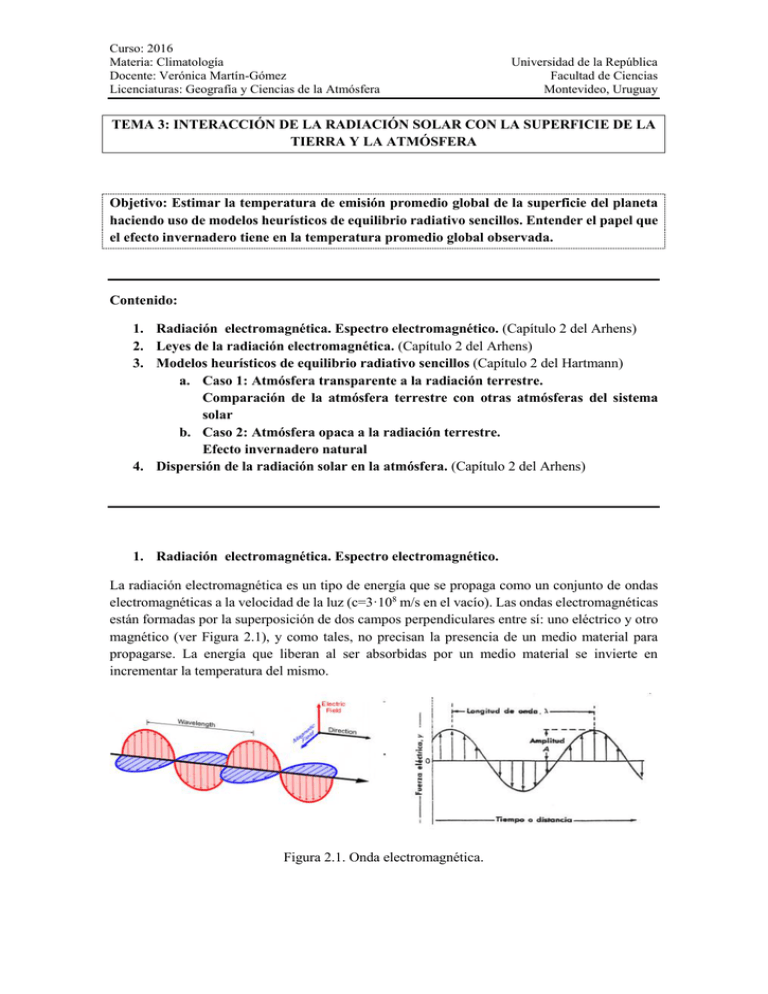
Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay TEMA 3: INTERACCIÓN DE LA RADIACIÓN SOLAR CON LA SUPERFICIE DE LA TIERRA Y LA ATMÓSFERA Objetivo: Estimar la temperatura de emisión promedio global de la superficie del planeta haciendo uso de modelos heurísticos de equilibrio radiativo sencillos. Entender el papel que el efecto invernadero tiene en la temperatura promedio global observada. Contenido: 1. Radiación electromagnética. Espectro electromagnético. (Capítulo 2 del Arhens) 2. Leyes de la radiación electromagnética. (Capítulo 2 del Arhens) 3. Modelos heurísticos de equilibrio radiativo sencillos (Capítulo 2 del Hartmann) a. Caso 1: Atmósfera transparente a la radiación terrestre. Comparación de la atmósfera terrestre con otras atmósferas del sistema solar b. Caso 2: Atmósfera opaca a la radiación terrestre. Efecto invernadero natural 4. Dispersión de la radiación solar en la atmósfera. (Capítulo 2 del Arhens) 1. Radiación electromagnética. Espectro electromagnético. La radiación electromagnética es un tipo de energía que se propaga como un conjunto de ondas electromagnéticas a la velocidad de la luz (c=3·108 m/s en el vacío). Las ondas electromagnéticas están formadas por la superposición de dos campos perpendiculares entre sí: uno eléctrico y otro magnético (ver Figura 2.1), y como tales, no precisan la presencia de un medio material para propagarse. La energía que liberan al ser absorbidas por un medio material se invierte en incrementar la temperatura del mismo. Figura 2.1. Onda electromagnética. Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay Las ondas electromagnéticas van a estar caracterizadas por una longitud de onda λ (distancia entre dos crestas consecutivas), una frecuencia υ, y un periodo P (la inversa de la frecuencia). La longitud de onda y la frecuencia cumplen la relación: c= λ· υ, donde c es la velocidad de la luz. Como c es constante, cuanto mayor es λ, menor es υ. La Figura 2.2 muestra el espectro de radiación electromagnética. Centrándonos en la franja del visible se puede ver que: i. ii. La radiación que nosotros podemos ver es la que se encuentra en la franja de los 400nm a los 750nm. La longitud de onda promedio del espectro visible sería de 500nm, aproximadamente. Este tamaño es del orden de la centésima parte del diámetro de un cabello humano. Dentro del visible, las longitudes de onda más largas están asociadas al rojo y las más cortas al violeta. Cuando las longitudes de onda empiezan a ser más grandes que los 750nm empezamos a hablar del infrarrojo, región del espectro electromagnético no visible por el ojo humano. Por el contrario, cuando empiezan a ser más pequeñas que los 400nm, entonces empezamos a hablar de la región del ultravioleta, tampoco visible para el ojo humano. Figura 2.2. Espectro electromagnético. 2. Leyes de la radiación electromagnética. Antes de introducir las leyes de la radicación es necesario entender qué se entiende por cuerpo negro, ya que todas estas leyes van a estar referidas a este tipo de cuerpos. Un cuerpo negro es un cuerpo ideal que se comporta como un absorbente perfecto de toda la radiación que le llega y como un emisor perfecto (emite la máxima radiación posible a su temperatura dada). En general, tanto la superficie de la Tierra como el sol absorben y emiten radiación con una eficiencia de aproximadamente el 100% para sus respectivas temperaturas, por lo que pueden ser considerados como cuerpos negros y se les pueden aplicar las leyes de la radiación que se exponen a continuación. a. Ley de Plank La intensidad de radiación emitida por un cuerpo negro en equilibrio termodinámico es función de la temperatura T y la longitud de onda λ: Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera B T donde c1 3.74 10 16 Universidad de la República Facultad de Ciencias Montevideo, Uruguay c15 cT2 e 1 Wm 2 y c2 1.45 10 2 mK . La figura 2.3 muestra los espectros de emisión de tres cuerpos negros con temperaturas absolutas T=5000K, T=6000K y T=7000K. En ella se puede observar que cuanto mayor es la temperatura del cuerpo, mayor es la intensidad de radiación emitida (área por debajo de las curvas). A su vez, también se puede ver que la emisión por parte de los cuerpos no es monocromática, sino que involucra una amplia gama de longitudes de onda. La longitud de onda asociada al máximo de intensidad radiativa emitida (λmax) aumenta conforme menor es la intensidad de ese máximo. Figura 2.3 Espectro de emisión de un cuerpo negro en función de la longitud de onda a una temperatura T dada. La Figura 2.4 muestra la intensidad de radiación emitida por el sol asumiendo que se comporta como un cuerpo negro (siguiendo la ley de Planck). En ella se puede ver que la mayor cantidad de energía emitida por el sol cae dentro de la banda del visible (44%), seguida del infrarrojo cercano (37%), infrarrojo lejano (11%) y del ultravioleta (7%). Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay Figura 2.4. Espectro electromagnético del sol según la ley de Planck. Figura 2.5. Espectros electromagnéticos del Sol y la Tierra en función de la longitud de onda. En la Figura 2.5 se puede ver una comparación de los espectros de emisión de la Tierra y del Sol. En ella podemos observar que mientras que el sol emite fundamentalmente en longitudes de onda menores a 2µm, la mayor parte de la radiación emitida por la superficie de la Tierra cae dentro del intervalo (5 – 35)µm (longitudes de onda mas largas). Por este motivo hablaremos de radiación de onda larga cuando nos refiramos a la radiación emitida por la Tierra y radiación de onda corta cuando nos refiramos a la radiación emitida por el Sol. b. Ley de Stefan – Boltzmann La ley de Stefann – Boltzmann estable que la energía que por unidad de tiempo y de superficie (irradiancia o densidad de flujo) emite un cuerpo negro es proporcional a Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay la cuarta potencia de su temperatura (cuanto mayor es la temperatura del cuerpo, mayor es la radiación total emitida por unidad de tiempo y de superficie): E (T ) T 4 donde es la constante de Stefann – Boltzmann (5.67·10-8Wm-2K-4) y T es la temperatura de emisión del cuerpo en kelvin (Temperatura en Kelvin = Temperatura en ºC + 273) y representa la temperatura a la que tiene que llegar un cuerpo negro para lograr estar en equilibrio termodinámico. Se obtiene integrando la ley de Planck a lo largo de todas las longitudes de onda y representa el área encerrada por debajo de la curva de la Ley de Planck (ver Figura 2.3). De este modo, y como se puede observar en las Figuras 2.3 y 2.4, cuanto mayor es la temperatura del objeto, mayor es la cantidad de energía total emitida por el mismo (mayor es el área debajo de la curva). El hecho de que la dependencia de la energía total emitida (E) sea con la cuarta potencia de la temperatura, hace que una duplicación la misma (Tfinal 2Tinicial) suponga un incremento de la energía emitida de un factor 16. De esta ley también se puede concluir que todo cuerpo con temperatura T > 0 K (es decir, T > -273ºC) emite energía en forma de radiación electromagnética. c. Ley de desplazamiento de Wien Derivando la ecuación de Planck respecto a la longitud de onda e igualando a cero se puede obtener el valor de la longitud de onda asociada al pico de emisión de Bλ(T): max 2897 T donde se expresa max en m y T en Kelvin. De este modo, conociendo el espectro de emisión de un cuerpo, podemos obtener el valor de la longitud de onda asociada al máximo de emisión y por ende, inferir su temperatura. Para el caso del sol, la temperatura de su superficie es de 6000k, aproximadamente, por lo que: max 2897 0.5m . Esto quiere decir que el sol emite la máxima 6000 cantidad de radiación cerca de las 0.5 µm (ver Figura 2.5). Sin embargo, para el caso de la Tierra la temperatura de la superficie es de 288K aproximadamente, por lo que el máximo de emisión se encuentra en las max 2897 10 m (ver Figura 2.5). 288 Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay En resumen: - - - - Un cuerpo negro es aquel que absorbe toda la radiación que le llega, y emite toda la radiación posible a la temperatura T que tiene. Toda la radiación posible que puede emitir un cuerpo negro sigue las leyes de Planck y Stefan-Boltzman. Todo cuerpo negro con una temperatura T, emite radiación electromagnética, y esa emisión no es monocromática, sino que abarca una amplia gama de longitudes de onda dentro del espectro electromagnético (Ley de Planck, Figura 2.3). Tanto la Tierra como el Sol emiten radiación. El sol, que es más cálido (6000K), emite la mayor parte de su energía en longitudes de onda menores que 1.5µm (ver Figura 2.5), con un máximo de emisión en la región del visible alrededor de las 0.5µm. La Tierra, bastante más fría (288K), radía casi toda su energía entre los 5 y 35 µm (ver Figura 2.5), con un pico de intensidad máxima en la región del infrarrojo alrededor de las 10µm. Como el sol emite en longitudes de onda más cortas que la Tierra, a la radiación solar la denominaremos radiación de onda corta y a la de la Tierra, radiación de onda larga. 3. Modelos heurísticos de equilibrio radiativo sencillos. El objetivo de este apartado es determinar la temperatura de emisión promedio global de la superficie del planeta basándonos en la utilización de modelos heurísticos de equilibrio radiativo sencillos. Un modelo heurístico es un esquema teórico de un sistema que se elabora para facilitar el estudio y comprensión del mismo. El que a estos modelos los llamemos de “equilibrio radiativo” quiere decir que no van a considerar la existencia de flujos de energía no radiativa (como son los flujos de calor latente y sensible). La temperatura promedio global de la superficie del planeta son 15ºC. Esta temperatura se ha mantenido aproximadamente constante a lo largo del tiempo. Esto implica que la misma cantidad de energía que por unidad de tiempo y de superficie llega a la Tierra, tiene que ser emitida por la misma. De no ser así, si la energía total que llega es mayor (menor) que la que el planeta emite, entonces el planeta se calienta (enfriando). Como sabemos que esto último no ocurre, pues la temperatura promedio global del planeta se ha venido manteniendo constante, se debe cumplir: Energía _ total Energía _ total Llega _ a _ la Tiempo Superficie emite _ la Tiempo Superficie sup erficie sup erficie ecuación _ equilibrio energétic Este balance de energía se establece entre la energía radiante emitida por el sol e incidente en la superficie del planeta, y la energía emitida en forma de radiación por la superficie de la Tierra. En los dos siguientes apartados calcularemos la temperatura de emisión de la superficie de la Tierra considerando la ecuación de equilibrio energético anterior y dos casuísticas distintas. Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay 3.1 Modelo heurístico de equilibrio radiativo sencillo. Caso 1: Atmósfera transparente a la radiación terrestre. El caso 1 representa el modelo heurístico más sencillo de todos. Se parte de la asunción de las siguientes hipótesis de partida: - La atmósfera es transparente tanto a la radiación solar como a la emitida por la superficie de la Tierra. No se consideran flujos de energía que no sean radiativos. Esto quiere decir que no se tienen en cuenta los flujos de calor latente y sensible. Albedo planetario p 0.30 . (El albedo planetario representa la cantidad total de la radiación solar incidente que es refleja hacia el espacio sin ser absorbida. Esta cantidad considera no sólo el albedo de la atmósfera sino que también el de los diferentes tipos de superficies de la Tierra). Considerando la ecuación de equilibrio energético anterior, Energía _ total Energía _ total , la energía total que por Llega _ a _ la Tiempo Superficie emite _ la Tiempo Superficie sup erficie superficie unidad de tiempo y de superficie emite la superficie de la Tierra viene dada por la ley de StefanBoltzmann. Es decir: Energía _ total 4 ·Tsup erficie emite _ la Tiempo superficie Stefan Boltzmann En esta ecuación Tsup erfcie es la temperatura de emisión de la superficie de la Tierra. Representa la incógnita que queremos calcular. Lo que necesitamos saber es cuánto vale la energía total que por unidad de tiempo y de superficie Energía _ total . Para ello tenemos que calcular Tiempo Superficie Llega _ a _ la llega a la superficie de la tierra sup erficie cuánta de toda la radiación emitida por el sol llega a la superficie de la Tierra. Se sabe que energía que por unidad de tiempo emite el sol (luminosidad) es Lo=3.9·1026W (recuérdese que 1watt = 1J/s). Esa cantidad es emitida por el sol en todas las direcciones del espacio, distribuyéndose en esferas concéntricas con el sol de radio ‘d’. Entonces, sabiendo que la distancia Tierra-Sol es dTS=1.5·1011m, y que la superficie de radio dTS concéntrica con el sol 2 viene dada por 4d TS , la energía que por unidad de tiempo y de superficie llega a una esfera de radio igual a la distancia Tierra-Sol es: S 0 L0 . S0 se conoce con el nombre de constante 4d TS2 solar y es constante a lo largo de toda la superficie de dicha esfera de radio dTS. Teniendo en cuenta que dTS=1.5·1011m, la constante solar para el caso de la Tierra vale: S0=1367Wm-2, y representa la cantidad neta de energía que por unidad de tiempo y de superficie llega a la cima de la atmósfera terrestre. Ahora bien, esa energía que por unidad de tiempo y de superficie llega a la Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay cima de la atmósfera es interceptada por la superficie circular y perpendicular al haz de radiación solar de área R 2 (ver Figura 2.6), donde R es el radio de la Tierra (* en realidad R debería ser la suma del radio de la tierra mas es del espesor de la atmósfera, pero dado que el espesor de la atmósfera es muy pequeño en comparación con el radio del planeta, como simplificación vamos a despreciar el espesor de la atmósfera y sólo consideraremos el radio del planeta). Por lo tanto, la energía que por unidad de tiempo llega a la cima de la atmósfera es: S 0 ·R 2 . Ahora bien, el albedo planetario refleja el 30% de la radiación solar incidente en el tope de la atmósfera, por lo que energía total que llega a la superficie de la tierra será: Energía _ total S 0 1 p R 2 Llega _ a _ la Tiempo sup erficie Esta energía que por unidad de tiempo llega a la superficie de la tierra es completamente absorbida por la misma. Dicha cantidad será redistribuida por toda la superficie del planeta. Por tanto: S 0 1 p R 2 S 0 1 p Energía _ total Llega _ a _ la 4 4R 2 Tiempo Superficie sup erficie Con esto ya conocemos la energía total procedente del sol que por unidad de tiempo y de superficie llega a la superficie de la tierra, y la que emite la propia superficie terrestre. En equilibrio energético ambas deben ser iguales: Energía _ total Energía _ total Llega _ a _ la emite _ la Tiempo Superficie Tiempo Superficie superficie sup erficie Y por lo tanto: S 0 1 p R 2 4 4 4 ·Tsup erficie Tsup erficie S 0 1 p 4 Tsuperficie 255 K 18º C O sea, la temperatura de emisión de la superficie de la Tierra resulta ser de -18ºC, valor que es mucho menor que la media global observada de 15ºC. Para entender esta diferencia, es necesario considerar el efecto invernadero. La atmósfera terrestre en realidad tiene un comportamiento bastante opaco para la radiación de onda larga emitida por la Tierra. En la sección 3.2 consideraremos un modelo heurístico sencillo de equilibrio radiativo en el que se contemple la existencia de una atmósfera que absorbe radiación de onda larga emitida por la superficie. Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay Figura 2.6. Esquema del haz de radiación solar incidente en la Tierra. 3.1.1 Comparación de la atmósfera Terrestre con otras atmósferas del sistema solar. Como se ha podido ver, la temperatura de emisión de la superficie de los planetas viene dada por la expresión: Tsuperficie 4 S 0 1 p 4 , donde se puede ver claramente su dependencia con la constante solar So (y por lo tanto, de la distancia del planeta al sol) y el albedo. A través de la curva negra de la Figura 2.7 se puede ver que la temperatura de emisión promedio global de la superficie de los planetas disminuye conforme la distancia del planeta al sol crece. En la ecuación de la Tsuperficie , la dependencia con la distancia del planeta a la estrella viene dada a través de la constante solar So. A su vez, en la Figura 2.7 se muestra la temperatura de emisión de algunos planetas del sistema solar (círculos blancos) junto con la temperatura observada (círculos negros) de cada uno de ellos. En general se puede ver que todos los planetas presentan una temperatura mucho superior a la que se obtiene estableciendo un equilibrio radiativo en la superficie de cada uno de los planetas. Esa diferencia entre la temperatura de emisión calculada considerando el primer caso de modelo heurístico y la observada está asociada al efecto invernadero. En la Tabla 1 se muestran los valores de la temperatura de emisión de cada uno de los planetas del sistema solar. Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay Figura 2.7. Temperatura de emisión de la superficie (circulo blanco) y la observada (círculo negro) de algunos de los planetas del sistema solar. La curva negra representa la dependencia de la temperatura de emisión con la distancia del planeta al sol. Planeta Distancia Albedo Constante Te (ºC) a sol (m) solar 0,058 9225,7 169 Mercurio 5.80·1010 0,71 2660,7 -32 Venus 1.08·1011 0,3 1379,3 -18 Tierra 1.50·1011 11 0,16 597,0 -56 Marte 2.28·10 11 0,34 51,3 -163 Júpiter 7.78·10 0,34 15,2 -1912 Saturno 1.43·1012 0,34 3,8 -21 Urano 2.87·1012 12 0,29 1,5 -226 Neptuno 4.50·10 Tabla 1. Temperatura de emisión de cada uno de los planetas del sistema solar en función de su distancia al sil y albedo. 3.2 Modelo heurístico sencillo de equilibrio radiativo. Segundo caso: Atmósfera opaca a la radiación terrestre. En el primer caso (apartado 3.1) se consideró que la atmósfera era transparente a la radiación emitida por la superficie de la Tierra cuando en realidad la mayoría de los componentes minoritarios de la atmósfera actúan absorbiendo la radiación de onda larga emitida por la superficie de la Tierra. En este segundo caso vamos a considerar la existencia de una atmósfera Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay opaca a la radiación de onda larga emitida por la superficie terrestre. Las hipótesis de partida en este segundo caso son: - - La atmósfera es transparente a la radiación solar. La atmósfera es opaca a la radiación emitida por la superficie de la Tierra (absorbe toda la radiación de onda larga emitida por la superficie terrestre) y a su vez la reemite en todas las direcciones del espacio. No se consideran flujos de energía que no sean radiativos. Esto quiere decir que no se tienen en cuenta los flujos de calor latente y sensible. El albedo planetario p 0.30 . En este modelo, la radiación solar que llega a la superficie del planeta es absorbida por el mismo. Esa absorción de radiación se invierte en un calentamiento de la superficie del planeta. Pero a su vez, por el hecho de tener una temperatura T, la Tierra también va a emitir también radiación (radiación de onda larga). Como en este modelo se considera que la atmósfera es opaca a la radiación terrestre, los gases efecto invernadero absorberán esta radiación para posteriormente reemitirla en todas las direcciones. En esa reemisión de radiación, parte escapa al espacio y otra parte se va hacia la superficie. De este modo, en este segundo caso la superficie de la tierra no sólo recibe la radiación emitida por el sol, sino que también aquella que reemiten los gases efecto invernadero de la atmósfera. La Figura 2.8 muestra una representación esquemática del problema. En este caso, como la atmósfera presenta un papel dentro del balance global de energía del planeta, a la hora de establecer el balance de energía no sólo lo tendremos que hacer en la superficie de la tierra, sino que también en la atmósfera. Figura 2.8. Esquema del efecto invernadero. Balance de energía en superficie: S0 1 p TA4 TS4 4 Balance de energía en la atmósfera: TS4 TA4 TA4 (1) (2) Despejando TA de la ecuación (2) e introduciéndola en (1) se obtiene: 4 Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay S0 1 p 1 TS4 TS4 4 2 S0 1 p 1 TS4 TS4 S0 1 p TS 4 S0 1 p 303K 30º C 4 2 2 2 Este resultado muestra una temperatura de la superficie mucho más cálida como consecuencia de que ésta no sólo absorbe la radiación de onda corta procedente del sol, sino que también absorbe la radiación infrarroja emitida por los gases efecto invernadero de la atmósfera. A este fenómeno se le conoce como efecto invernadero natural. Ahora bien, con este segundo caso hemos obtenido una temperatura de 30ºC. Este valor excede los 15ºC observados. El “por qué” de este exceso tiene dos razones: (1) La absorción de radiación por parte de los gases efecto invernadero de la atmósfera es selectiva. La figura 2.9 muestra las bandas de absorción de radiación de los gases efecto invernadero. En ella se puede ver que el gas efecto invernadero más importante en el vapor de agua, seguido del dióxido de carbono y el ozono. Otros gases importantes, también absorbentes selectivos, son el óxido nitroso, y el metano. Dentro de la Figura 2.9, la situada abajo representa el espectro de absorción total (la suma de los espectros de absorción de radiación de todos los gases efecto invernadero de la atmósfera). En ella se puede ver la existencia de una región ubicada entre las (8-11)µm conocida como “ventana atmosférica” en la que la mayoría de los gases efecto invernadero no absorbe radiación. Esa radiación emitida por la tierra escaparía directamente hacia el espacio. En el segundo caso de modelo heurístico se consideró que toda la radiación emitida por la superficie de la Tierra es absorbida por la atmósfera, pero si se tomase en cuenta la existencia de esta ventana en la que no existe absorción por parte de los gases efecto invernadero, la temperatura de la superficie del planeta sería más pequeña que la obtenida. (2) No se están considerando los flujos de calor latente y sensible que actúan enfriando la superficie del planeta. Finalmente, como vimos en el Tema 1, las nubes presentaban fundamentalmente dos papeles dentro del balance de energía global del planeta, uno era a través del albedo y el otro era a través de su participación dentro del efecto invernadero. Pues bien, las gotas de agua de las nubes pueden también presentan una absorción selectiva y contribuyen al efecto invernadero “taponando” la ventana atmosférica, es decir, absorbiendo longitudes de onda que caen dentro de la ventana atmosférica. Del mismo modo, los CFCs, gases de efecto invernadero de emisión antropogénica, también contribuyen al efecto invernadero absorbiendo radiación dentro de la ventana atmosférica. Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay Figura 2.8 Absorción de radiación por los gases de la atmósfera. Las áreas sombreadas representan el porcentaje de radiación absorbida por cada gas. Los gases que mas absorben la radiación infrarroja emitida por la superficie de la Tierra son el vapor de agua y el dióxido de carbono. La gráfica de más abajo representa el porcentaje de radiación absorbida por todos los gases de la atmósfera en conjunto. Curso: 2016 Materia: Climatología Docente: Verónica Martín-Gómez Licenciaturas: Geografía y Ciencias de la Atmósfera Universidad de la República Facultad de Ciencias Montevideo, Uruguay 4. Interacción de la radiación solar con la atmósfera. Cuando la radiación solar entra en la atmósfera, numerosas interacciones tienen lugar. Por ejemplo, parte de la energía solar es absorbida por los gases de la atmósfera, tales como el ozono en la estratosfera media o el nitrógeno y oxígeno molecular en la termosfera. Existen también otros dos tipos de interacciones: el scattering y el albedo (éste último ya vimos lo que era). El scattering consiste en la dispersión de la luz en todas las direcciones del espacio como consecuencia de la presencia de moléculas gaseosas o partículas de polvo en suspensión en la atmósfera. A este fenómeno se le conoce como dispersión de Rayleigh y a la radiación dispersada también se le conoce como radiación difusa. La intensidad de la dispersión, S , es proporcional a r : la cuarta potencia del cociente r S 2 4 Donde S es a intensidad de la dispersión, r es el radio de la partícula y la longitud de onda. Por un momento, supongamos un valor de r contante. La dispersión, S, será más intensa cuanto menor sea la longitud de onda. Si bien las moléculas del aire son muy pequeñas con respecto a la longitud de onda de la luz visible, dentro del rango de longitudes de onda del espectro visible, las moléculas del aire son mucho más efectivas dispersando longitudes de onda más cortas (azul) que las largas (rojo). Si tenemos en cuenta que azul 0.47 m y rojo 0.64m , el cociente S azul 3.45 la dispersión del azul es 3.45 veces superior a la dispersión del rojo en la S rojo atmósfera. Por consiguiente, cuando miramos al cielo lo vemos azul. Sin embargo, al atardecer el sol se ve rojizo. Esto es consecuencia de que los rayos del sol tienen que atravesar una capa de atmósfera más grande, a la que únicamente los rayos rojos “sobreviven”. Referencias: Capítulo 2 de Hartmann, D. L. (2015). Global physical climatology. Capítulo 2 de Ahrens, C. D. (1987). Meteorology Today: an introduction to weather, climate, and the environment.