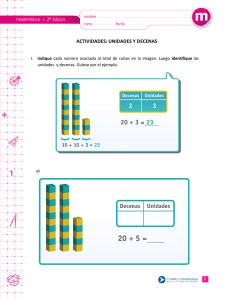
+ matemática x aschero

+ MATEMÁTICA
X ASCHERO
(BUENOS AIRES, 2016)
1
1. Una mirada desprejuiciada sobre el sistema de numeración
Sólo es igual lo igual
No cabe duda. Para satisfacción de Aristóteles, vivimos en un mundo de objetos:
aquí veo una mesa, allá una banana y más allá un edificio y una estrella. Hasta
nosotros mismos nos percibimos como un objeto más dentro del mundo, y percibimos
también como entidades separadas a las otras personas.
Ahora bien, mentalmente podemos establecer entre los diversos objetos que
pueblan el universo distintos tipos de relaciones. Al menos teóricamente, cuando
comparamos dos o más objetos pueden ocurrir tres cosas diferentes: a) los
objetos son exactamente iguales; b) los objetos son totalmente diferentes; y c)
los objetos comparados presentan semejanzas y diferencias. Examinemos cada una
de estas posibilidades.
a) Los objetos comparados son exactamente iguales.- A poco que reflexionemos
sobre esta primera posibilidad, deberemos descartarla porque, si dos objetos son
exactamente iguales, entonces se trata del mismo objeto. Ni siquiera dos gemelos
univitelinos son exactamente iguales: el hecho de ocupar espacios distintos ya
los diferencia. La historia de la filosofía ha establecido ya el supuesto de la
imposibilidad de la existencia de dos cosas exactamente iguales, por ejemplo con
el Principio de los Indiscernibles de Leibniz. Veamos ahora qué pasa con
nuestra segunda posibilidad.
b) Los objetos comparados son totalmente diferentes.- Esta es otra opción que
debemos descartar, aún cuando comparemos objetos tan diferentes como una
manzana, una galaxia y una piedra. Dichos objetos no son total y radicalmente
diferentes porque comparten al menos una característica en común: "son", es
decir, son entes, objetos. Desde ya, estamos aquí en un nivel muy alto de
abstracción, que es el territorio propio de los filósofos.
2
Es fácil discernir que tienen en común un triángulo y un cuadrilátero. Son
polígonos. Sin embargo no es tan fácil discernir qué tienen en común un polígono
y el aire. Por más diferentes que sean los objetos entre sí siempre
encontraremos algo en común: ambos son objetos en el sentido filosófico del
término, es decir, "son". Esta y otras características tan genéricas de los
entes son estudiadas por una rama de la filosofía, que es la metafísica.
c) Hemos concluido la imposibilidad de que dos objetos sean exactamente iguales,
o que sean totalmente diferentes. Debemos admitir, entonces, la tercera y única
posibilidad restante: si los objetos no son exactamente iguales tienen
diferencias, y si no son totalmente distintos es porque presentan semejanzas.
Por lo tanto, concluimos que todos los objetos presentan siempre entre sí
semejanzas y diferencias.
3
4
No todas las pérdidas son iguales
El infranúmero es un nuevo concepto matemático que determina la diversidad de lo no
existente, actuando como una alternativa eficaz y lógica ante la invariabilidad del cero
tradicional que no tiene en cuenta el desarrollo de las diversas operaciones que
finalizan o pasan por él.
Desde el momento en que existe un dato distinto a la nada (singularidad irrepetible),
contamos con una energía numeral que llegará a ser infranumeral en el caso de lograr
su completa interferencia con las operaciones lógicas del sistema.
El infranúmero es la energía resultante de una operación de interferencia total, con la
interferencia parcial se está dentro de la zona numeral o ultranumeral.
El infranúmero determina una nueva noción matemática de fundamental importancia
con el fin de poder operar sobre cantidades de elementos que expresan medidas de
entidades no materiales.
Es energía cuantificada neutra surgida de todas las pérdidas operativas.
Se considera físicamente interferencia cuando dos ondas se superponen en oposición
de fase.
Si las ondas son de igual frecuencia y amplitud, la interferencia resulta total,
(infranúmero).
Desde el punto de vista acústico, si se colocan dos tubos de órgano iguales,
supongamos que de una frecuencia de 256 Hz. cada uno; acoplados a la misma caja
de aire y se sopla en ambos, no oiremos un sonido más fuerte, sino sólo el aire que
escapa.
También un haz de luz viene a estar compuesto por un tren de ondas. Cuando dos
haces luminosos de iguales características chocan entre sí, su energía se interfiere
provocándose la oscuridad; pero la energía no ha desaparecido.
Una de las reglas fundamentales de la física dice que la energía no puede
desaparecer.
Tal es la ley de conservación de la energía.
En el fenómeno de la interferencia hay una energía que ha dejado de existir en forma
de luz.
Por tanto, tiene que aparecer una cantidad exactamente igual de energía en otra forma
distinta; y en este caso es el calor.
Supongamos que damos cuerda al resorte de un reloj; ahora contiene más energía
que cuando estaba distendido.
A continuación disolvemos el resorte todavía tenso, en un ácido. ¿Qué ocurre con la
energía?
También aquí se convierte en calor.
5
Si empezamos con dos soluciones ácidas a la misma temperatura y disolvemos en
una de ellas el muelle distendido y en la otra un muelle tenso (por lo demás idénticos),
la segunda solución tendrá al final una temperatura mayor que la primera.
La propia materia es una forma de energía.
Por otro lado, el lenguaje matemático incurre algunas veces en inexactitudes debido a
su limitada capacidad para representar ciertos resultados.
Esto se soluciona en parte al incorporar la serie infranumeral.
Todo movimiento que salga, pase o llegue por el punto infranumeral es algo que debe
ser medido con exactitud.
6
Entre la nada y el todo
Así como el infranúmero cuestiona la existencia del cero como único símbolo
representativo de la nada, el ultranúmero actúa como símbolo inverso de aproximación
al concepto del todo, identificado tradicionalmente por el infinito y en el modelo de
Aschero con el ultra cero. Un mismo punto bidireccional de polo positivo y negativo,
origina y finaliza lo incontable, que se extiende más allá y más acá de toda serie
numérica, tanto como se desee. Si el número avanza, el ultranúmero retrocede y en la
medida que se aleja su magnitud decrece, con lo cual se invierten todas las
operaciones aritméticas. Con el número y el infranúmero se cuenta, con el ultranúmero
se descuenta. El absoluto es mensurable mediante el ultra cero, y así se define uno de
los límites que ayuden de una vez por todas a solucionar alguno de los enigmas y
contradicciones más importantes del lenguaje matemático. Para esto se establece la
serie ultranumeral.
Es tan lógico contar a partir de la nada como descontar a partir del todo.
Cada ultranúmero que proceda del todo es algo que debe ser medido con exactitud,
para así establecer su magnitud, que tiene una progresión decreciente en la medida
que se aleja de su punto de partida: el ultra cero.
La serie ultranumeral es ilimitada y se utiliza indistintamente para los ultranúmeros
reales y los imaginarios.
7
1 : 0 = 1 (uno dividido cero es igual a ultra uno)
De esta forma la Ecuación de Wallis se resuelve: ultra uno es el uno más grande que
existe ya que es el número uno más próximo al ultra cero. En cambio, lo que es
imposible de determinar es el ultranúmero menor (el de mayor cantidad de cifras).
La frontera (o el puente) que vincula a los números con los ultranúmeros para permitir
el traspaso entre ambos es (por ahora) el gúgolduplex.
El gúgolduplex es uno de los números más grandes a los que se puso nombre. Así
como una hoja de papel lo suficientemente grande como para escribir todos los ceros
de un gúgolplex es más grande que el universo conocido, entonces, una hoja de papel
lo suficientemente grande como para escribir un gúgolduplex sería más grande que un
gúgolplex de universos como el nuestro.
Para la recta numérica el gugoldúplex es un meganúmero finito, y al pasar dicha
frontera se convierte en un ultranúmero muy pequeño, por la ley de la inversión que el
mundo ultranumeral establece, determinando que los ultranúmeros más grandes,
poseen las cifras más pequeñas:
Veamos ahora la serie de los primeros veintiséis ultranúmeros primos, empezando por
el mayor (ultra uno) y finalizándola con el menor de ellos (ultra noventa y siete).
1 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
Si no se considera al número uno como primo y sí al número dos, evidentemente el
número primo más grande es ultra dos.
Existe un puente que permite el tránsito numérico a través del Gúgolduplex que
convertido en Ultra Gúgolduplex fija el punto de conversión para arribar al número
mayor de las matemáticas: el ultra cero.
Si los matemáticos crean un número mayor al Gúgolduplex lo único que se debe hacer
es cambiar el puente de lugar realizando la misma conversión y, obviamente
recorriendo un camino más largo para arribar al mayor número que existe.
Los ultranúmeros fijan lo mayor (ultra cero) pero en cambio pierden la posibilidad de
fijar lo menor (ultra infinito). Ese es el sacrificio necesario para obtener un resultado
óptimo en uno de los extremos que históricamente nunca se logró.
8
Tomando como punto de partida el plano numérico tradicional con todos sus atributos,
que como sabemos es de posición horizontal, Sergio Aschero propone insertar un
segundo plano perpendicular al anterior en posición de atravesar centradamente el
primer plano.
9
Los infranúmeros con su capacidad de cuantificar las pérdidas y los ultranúmeros con
la suya de establecer un lugar preciso para los números imposibles de fijar mediante la
matemática tradicional, hacen de esta dualidad algo similar a la capacidad del dios
Jano con su posibilidad de ver simultáneamente el ayer y el mañana.
Los números son el "Big Bang” y los ultranúmeros el "Big Crunch". Lo que no se
detiene es la suma temporal (númérica) entre un fenómeno y el otro.
10
Nuevo modelo decimal
En un principio para contar, la gente usó los cinco dedos de una mano, y así apareció
la numeración en base cinco.
Hasta hace pocos años este sistema era ampliamente usado en Oriente.
Los ábacos elementales que todavía se encuentran en China y Japón, están
diseñados con este código.
También fue muy utilizado el sistema de numeración romano basado en siete letras.
Es también fácil ver como el diez ha llegado a ser un número importante, motivado
porque el ser humano tiene diez dedos en las manos y diez en los pies.
Las primeras aportaciones tienen miles de años, pero, curiosamente nuestra manera
actual de escribir los números es bastante reciente: utilizada ya por los hindúes, y
difundida por los árabes, no llegó a Europa hasta el siglo XIII.
Durante siglos hubo una verdadera guerra entre los partidarios del sistema literal
romano y del numeral arábigo.
Veamos las diferencias:
Un romano al observar tres rayas verticales trazadas en la arena (durante el imperio
de la antigua Roma), habría entendido que el número representado es tres (III),
mientras que para un romano actual el mismo diseño significaría (111).
11
Cada uno sigue un código distinto y ambos son coherentes.
Para uno, las tres rayas significan:
1+1+1=3
Y para otro:
100 + 10 + 1 = 111
La gran diferencia entre uno y otro, no está tanto en los signos mismos, como en la
forma de relacionarlos. El romano es aditivo y sustractivo, el arábigo es además
posicional. De allí su poder.
El número es una noción matemática de fundamental importancia, introducida de
manera más o menos consciente desde la antigüedad, con el fin de poder operar
sobre cantidades de elementos que constituyen conjuntos o sobre cantidades que
expresan medidas de entidades materiales.
El código decimal presenta algunas deficiencias que empezaremos a señalar.
12
13
2. La genetización numérica
La genética es la rama de la biología que se encarga del estudio de aquello es
transmitido en sucesivas generaciones a través de los genes. El concepto
también hace referencia a lo que se vincula con el comienzo; el inicio o la raíz de
algo.
La genética; por lo tanto; analiza cómo se transmite la herencia de la biología de un
individuo a otro. Su principal objetivo es explicar la manera en que los rasgos y
diversas cualidades pasan de los padres a sus descendientes.
Estas transferencias se desarrollan mediantes los genes; compuestos por fragmentos
de ácido desoxirribonucleico o ADN; una molécula que se encarga de la
codificación de los datos genéticos presentes en las células.
El ADN; que controla las funciones; el comportamiento y la estructuración de cada
célula; tiene la capacidad de replicarse y producir una copia de sí mismo.
La mitosis es un proceso de división celular en la que las dos células resultantes
obtienen exactamente la misma información genética de la célula progenitora.
La meiosis; es una manera de reproducción celular; en la que a diferencia de la
mitosis; las células hijas contienen la mitad de los cromosomas; es decir; su número
es haploide; y su número de ADN es 1. Esta forma de reproducción celular; es
utilizada por el organismo para crear células sexuales llamados gametos.
14
El factor determinante para que los hijos sean semejantes a los padres es la herencia; ya que
al aportar en un espermatozoide y en un óvulo 23 cromosomas cada uno para lograr la
concepción; aportan los genes; que son partículas que contienen rasgos del padre y de la
madre; transmitiendo características de los progenitores a los hijos.
Los genes son pequeñísimas partículas constituidas por cadenas de ácidos que contienen
potencialmente rasgos y características provenientes del padre y de la madre; y a través de
ellos de sus antecesores.
En su investigación matemática; el genetizador de Sergio Aschero mira hacia el
pasado; el presente y el futuro de cada número entero; estableciendo sus principios
reproductivos y hereditarios; basándose en una combinatoria de dos variables sin
repetición. El pasado es fragmentario; el presente unívoco y el futuro totalizador.
Pasado y futuro están espejados (tienen las mismas cifras pero no el mismo sentido).
Sólo el presente es único e irrepetible.
En los tres primeros números genetizados (1, 2, 3), se pueden hacer algunas
asociaciones: el número 1 es lo masculino; pero también se puede entender como una
línea en un plano (a); el número 2 es lo femenino; pero también se puede entender
como un ángulo (a), (b); y el número 3 que es lo engendrado por la unión del 1 y el 2;
se puede entender como un triángulo (a), (b), (c); constituyéndose en la primera figura
geométrica. De ahí sus extraordinarias cualidades. También entre 1, 2 y 3 en la serie
de Fibonacci existe una continuidad entre los tres números que luego se pierde
definitivamente: 0, 1, 1, 2, 3, 5, 8, 13, 21…
Veamos que pasa al genetizar algunos números:
El pasado del número 1 es el 1, el presente del número 1 es el 1 y el futuro del número
1 es el 1. El 1 es un número particular y el iniciador de todo. Su pasado; su presente y
su futuro son idénticos. Es un caso único.
En el caso del número 2, su pasado son los números 1,1; su presente es el número 2
y su el futuro es el número 11. Las variables son dos: 1,1 y 11. El 1,1 en el pasado y el
11 en el futuro. Es decir que la "vida del número 2" transcurre (con estas dos
variables) entre 1,1 y 11.
El número 3 tiene cuatro variables: 1,2; 2,1; 3; 12; 21. El presente y el futuro de 3 (y el
de todos los números que surgen de 3 es divisible por 3; generando en su resultado
números enteros; en cambio el pasado de todos los números; con la excepción del 1,
tiene decimales). Recordemos que 3 es además el único número primo puro.
Otro aspecto a tener en cuenta es que serie de números naturales agrupados y
sumados de tres en tres tienen la propiedad de ser siempre divisibles por 3.
1 + 2 + 3 = 6 (3x2)
4 + 5 + 6 = 15 (3x5)
7 + 8 + 9 = 24 (3x8)
10 + 11 + 12 = 33 (3x11)
13 + 14 + 15 = 42 (3x14)
15
16 + 17 + 18 = 51 (3x17)
19 + 20 + 21 = 60 (3x20)…
El número 4 tiene seis variables: 1,3; 2,2; 3,1; 4; 13; 22; 31.
El número 5 tiene ocho variables: 1,4; 2,3; 3,2; 4,1; 5; 14; 23; 32; 41.
El número 6 tiene diez variables: 1,5; 2,4; 3,3; 4,2; 5,1; 6; 15; 24; 33; 42; 51. (divisibles
por 3)
El número 7 tiene doce variables: 1,6; 2,5; 3,4; 4,3; 5,2; 6,1; 7; 16; 25; 34; 43; 52; 61.
El número 8 tiene catorce variables: 1,7; 2,6; 3,5; 4,4; 5,3; 6,2; 7,1; 8; 17; 26; 35; 44;
53; 62; 71.
El número 9 tiene dieciséis variables: 1,8; 2,7; 3,6; 4,5; 5,4; 6,3; 7,2; 8,1; 9; 18; 27; 36;
45; 54; 63; 72; 81. (divisibles por 3)
El número 10 tiene dieciocho variables: 1,9; 2,8; 3,7; 4,6; 5,5; 6,4; 7,3; 8,2; 9,1; 10; 19;
28; 37; 46; 55; 64; 73; 82; 91…
A continuación algunos números de la serie que nace de 3 con sus particulares
características de divisibilidad:
3 = 12; 21 (3x1; 3x4; 3x7)
6 = 15; 24; 33; 42; 51 (3x5; 3x8; 3x11; 3x14; 3x17)…
9 = 18; 27; 36; 45; 54; 63; 72; 81
12 = 111; 210; 39; 48; 57; 66; 75; 84; 93; 102; 111
15 = 114; 213; 312; 411; 510; 69; 78; 87; 96; 105; 114; 123; 132; 141
18 = 117; 216; 315; 414; 513; 612; 711; 810; 99; 108; 117; 126; 135; 144; 153; 162;
171
21 = 120; 219; 318; 417; 516; 615; 714; 813; 912; 1011; 1110; 129; 138; 147; 156;
165; 174; 183; 192; 201
24 = 123; 222; 321; 420; 519; 618; 717; 816; 915; 1014; 1113; 1212; 1311; 1410;
159; 168; 177; 186; 195; 204; 213; 222; 231
27 = 126; 225; 324; 423; 522; 621; 720; 819; 918; 1017; 1116; 1215; 1314; 1413;
1512; 1611; 1710; 189; 198; 207; 216; 225; 234; 243; 252; 261
30 = 129; 228; 327; 426; 525; 624; 723; 822; 921; 1020; 1119; 1218; 1317; 1416;
1515; 1614; 1713; 1812; 1911; 2010; 219; 228; 237; 246; 255; 264; 273; 282; 291
33 = 132; 231; 330; 429; 528; 627; 726; 825; 924; 1023; 1122; 1221; 1320; 1419;
1518; 1617; 1716; 1815; 1914; 2013; 2112; 2211; 2310; 249; 258; 267; 276; 285;
294; 303; 312; 321
16
36 = 135; 234; 333; 432; 531; 630; 729; 828; 927; 1026; 1125; 1224; 1323; 1422;
1521; 1620; 1719; 1818; 1917; 2016; 2115; 2214; 2313; 2412; 2511; 2610; 279; 288;
297; 306; 315; 324; 333; 342; 351
39 = 138; 237; 336; 435; 534; 633; 732; 831; 930; 1029; 1128; 1227; 1326; 1425;
1524; 1623; 1722; 1821; 1920; 2019; 2118; 2217; 2316; 2415; 2514; 2613; 2712;
2811; 2910; 309; 318; 327; 336; 345; 354; 363; 372; 381
42 = 141; 240; 339; 438; 537; 636; 735; 834; 933; 1032; 1131; 1230; 1329; 1428;
1527; 1626; 1725; 1824; 1923; 2022; 2121; 2220; 2319; 2418; 2517; 2616; 2715;
2814; 2913; 3012; 3111; 3210; 339; 348; 357; 366; 375; 384; 393; 402; 411
45 = 144; 243; 342; 441; 540; 639; 738; 837; 936; 1035; 1134; 1233; 1332; 1431;
1530; 1629; 1728; 1827; 1926; 2025; 2124; 2223; 2322; 2421; 2520; 2619; 2718;
2817; 2916; 3015; 3114; 3213; 3312; 3411; 3510; 369; 378; 387; 396; 405; 414; 423;
432; 441
48 = 147; 246; 345; 444; 543; 642; 741; 840; 939; 1038; 1137; 1236; 1335; 1434;
1533; 1632; 1731; 1830; 1929; 2028; 2127; 2226; 2325; 2424; 2523; 2622; 2721;
2820; 2919; 3018; 3117; 3216; 3315; 3414; 3513; 3612; 3711; 3810; 399; 408; 417;
426; 435; 444; 453; 462; 471
El Triángulo de Pascal o Tartaglia tiene un origen, como en muchos otros casos, muy
anterior al de estos dos matemáticos. Se tienen referencias que datan del siglo XII en
China. De hecho, algunas de sus propiedades ya fueron estudiadas por el matemático
chino Yang Hui (siglo XIII), así como por el poeta persa Omar Khayyam (siglo XII). El
que se le asocie el nombre del filósofo y matemático Blas Pascal (1623-1662), se debe
a que el francés escribió el primer tratado sobre el Triángulo. Lo de Tartaglia (15001557) viene porque el italiano fue el primero que lo publicó en Europa.
Hablando del Triángulo, este no es un triángulo en el sentido geométrico de la palabra,
sino una colección de números dispuestos en forma triangular que se obtienen de una
manera muy sencilla.
Como se puede observar, en la cúspide del Triángulo hay un 1, en la segunda fila hay
dos 1, y las demás filas empiezan con 1 y finalizan con 1, y cada número intermedio se
obtiene sumando los dos que se encuentran justo encima. Este Triángulo es infinito y
está relacionado con el desarrollo de las potencias de un binomio y con los números
combinatorios.
17
Sergio Aschero propone la creación de otra figura: la Pirámide de Aschero, cuya
estructura se basa en el proceso numérico establecido aquí.
Veamos su configuración:
18
3. La identiplicación numérica
La evolución, la que transformaría un pez en un filósofo, requiere que los componentes
químicos inertes se organicen formando un organismo vivo capaz de reproducirse a sí
mismo. Se supone que todos los tipos de vida han descendido, por medio de procesos
naturales, a partir de esta forma de vida "simple".
Para que esto fuera posible, debe haber existido algún proceso que pudiera generar la
información genética que observamos en los seres vivientes en la actualidad. El primer
organismo capaz de reproducirse tendría que haber hecho copias de sí mismo. La
evolución, para poder funcionar, requiere además que las copias no sean siempre
completamente exactas dado que ocurren modificaciones de la copia (mutaciones).
Cualquier mutación que capacite a un organismo a dejar más descendencia capaz de
reproducirse será pasada las generaciones posteriores. Esta "reproducción diferencial"
se llama selección natural.
El ácido desoxirribonucleico (polímero de unidades menores denominados
nucleótidos) junto con el ácido ribonucleico, constituye la porción prostética de los
nucleoproteidos, cuyo nombre tiene un contexto histórico, ya que se descubrieron en
el núcleo de la célula. Se trata de una molécula de gran peso molecular
(macromolécula) que está constituida por tres sustancias distintas: ácido fosfórico, un
monosacárido aldehídico del tipo pentosa (la desoxirribosa), y una base nitrogenada
cíclica que puede ser púrica (adenina ocitosina) o pirimidínica (timina o guanina).
La unión de la base nitrogenada (citosina, adenina, guanina o timina) con la pentosa
(desoxirribosa) forma un nucleósido; éste, uniéndose al ácido fosfórico, nos da un
nucleótido; la unión de los nucleótidos entre sí en enlace diester nos da el
polinucleótido, en este caso el ácido desoxirribonucleico. Las bases nitrogenadas se
hallan en relación molecular 1:1, la relación adenina + timina / guanina + citosina es
de valor constante para cada especie animal. Estructuralmente la molécula de ADN se
presente en forma de dos cadenas helicoidales arrolladas alrededor de un mismo eje
(imaginario); las cadenas están unidas entre sí por las bases que la hacen en pares.
Los apareamientos son siempre adenina-timina y citosina-guanina. El ADN es la base
de la herencia. Es la capacidad que tiene el ADN de hacer copias o réplicas de su
molécula. Este proceso es fundamental para la transferencia de la información
genética de generación en generación. Las moléculas se replican de un modo
semiconservativo. La doble hélice se separa y cada una de las cadenas sirve de molde
para la síntesis de una nueva cadena complementaria. El resultado final son dos
moléculas idénticas a la original.
El ADN es por lo común el constituyente básico de la cromatina (cromosoma) nuclear
en las células eucarióticas, pero también existe en pequeña cantidad en las
mitocondrias y cloroplastos. En los procariontes forma el nucloide (que a diferencia de
los eucariontes no va asociado a proteínas, es desnudo) y en los virus (DNA virus) que
lo poseen constituyen el virión o elemento infectante. Por lo común
su estructura tridimensional posee giro hacia la derecha (ß-ADN, dextrogiro) que es la
forma más estable y ocasionalmente posee giro hacia la izquierda (z-ADN, levógiro)
Acorde a las evidencias, sólo una pequeña parte del ADN constituye genes (menos del
10 %). Existen diferentes tipos que los podemos dividir en:
-ADN de copia única (el 57 % del total) formados por segmentos de aproximadamente
1000 pares de nucleótidos del longitud, una pequeña parte de este ADN contiene los
genes.
-ADN repetitivo (20 %) son unidades de aproximadamente 300 pares de nucleótidos
19
(es una molécula compleja formado por una base nitrogenada, un hidrato de carbono y
un grupo fosfato (ácido fosfórico inorgánico), unidos entre sí por enlaces covalentes)
que se repiten en el genoma unas 105 veces (unidades de repetición) y se intercalan
con el ADN de copia única.
-ADN satélite (altamente repetitivo: 28 %) son unidades cortas de pares de nucleótidos
que se repiten en el genomio. Son característicos en cada especie y pueden ser
separados por centrifugación. Constituyen la heterocromatina y no se le
conoce función.
Los porcentajes indicados son del hombre y el ratón, y las proporciones serían las
mismas en otras especies.
Las bases nitrogenadas son anillos heterocíclicos compuesto además del carbono
e hidrógeno por nitrógeno. Son de dos tipos fundamentales, las bases púricas (por
ser derivadas de la purina, de dos anillos heterocíclicos) y las bases pirimídicas (por
ser derivadas de la pirimidina de un solo anillo).
Dichas bases son cinco, pero en realidad solamente cuatro aparecen en el ADN. Las
bases púricas presentes son la adenina y guanina. Las bases pirimídicas son la
citosina y la timina (el uracilo es característico del ARN).
Si bien para la constitución del ADN se unifica a un solo grupo fosfato, existen en las
células una serie de nucleótidos de
singular importancia en el metabolismo celular. Estos producen enlaces muy ricos de
energía y los di- y tri- nucleótidos como el adenosin-tri-fosfato (ATP) son los
encargados de muchos procesos metabólicos.
Debe contener información útil biológicamente y que pueda trasmitirse sin
alteraciones. Por lo tanto debe permitir su duplicación para permitir el paso de célula a
célula y de generación en generación. Por otra parte debe ser capaz de
producir materia viva (proteínas) a partir de dicha información. Y deberá ser capaz de
variar ocasionalmente, para favorecer los cambios evolutivos y de adaptación.
La función principal del ADN es mantener a través de un sistema de claves
(código genético) la información necesaria para que las células hijas sean idénticas a
las progenitoras (información genética). Este proceso se almacena en la secuencia de
las bases (aparentemente aleatoria), que tiene una disposición que es copiada al ARN
para que en el ribosoma sintetice determinada proteína. Este proceso es también
denominado "dogma central de la biología molecular". Por medio de los mecanismos
de recombinación y mutaciones se obtienen las variaciones necesarias para
adaptaciones y evoluciones.
El núcleo dirige las actividades de la célula y en él tienen lugar procesos tan
importantes como la autoduplicación del ADN o replicación, antes de comenzar la
división celular, y la trascripción o producción de los distintos tipos de ARN, que
servirán para la síntesis de proteínas.
La mitosis es la división celular que consiste en que a partir de una célula se obtienen
dos células hijas, genéticamente idénticas a la madre. Se produce en cualquier célula
eucarionte, ya sea diploide o haploide y como mantiene invariable el número de
cromosomas, las células hijas resultarán diploides, si la madre era diploide o haploide.
La división del citoplasma se llama citocinesis, y la división del núcleo, cariocinesis.
Algunas células no realizan mitosis y permanecen en un estado interfásico, pero otras
la realizan frecuentemente (células embrionarias, células de zonas de crecimiento,
células de tejidos sujetos a desgaste.).
Función: crecimiento y desarrollo del organismo multicelular, y la regeneración de
tejidos expuestos a destrucción de células. En unicelulares, cumple la función
de reproducción asexual.
Cada mitosis está precedida por una interfase, donde se produce la duplicación del
20
material genético. Actúa como un mecanismo que asegura que cada célula hija reciba
la misma información genética.
Etapas: Profase, Pro metafase, Metafase, Anafase y Telofase.
Resultado de una división mitótica es la obtención de dos células hijas con igual carga
cromosómica, o sea, de una célula diploide con su carga cromosómica diploide se
obtienen dos células hijas también diploides. Siguiendo el principio de que los
cromosomas hermanos (homólogos) no pueden ir a un mismo polo y se distribuyen
aleatoriamente. El núcleo celular es un corpúsculo contenido en el citoplasma de las
células animales y vegetales, que contiene los cromosomas y es centro de información
que dirige la síntesis proteica. Su forma es variable (redondo, oval o elíptico, etc.),
su volumen es relativo (pero la relación núcleo-citoplasma es constante); ocupa una
posición central en la célula (en general), pero puede estar situado parietalmente. En
todas las células existe un núcleo, pero también hay células binucleadas y
plurinucleadas. El núcleo se halla rodeado por una membrana nuclear atravesada por
poros. Los núcleos presentan un doble aspecto según se hallen en reposo o en etapa
de división celular. En período de reposo se observan en su interior nucleolos. Su
composición química es compleja (proteínas, lípidos, compuestos inorgánicos, ADN,
ARN, protaminas e histonas).
En su interior se encuentra los cromosomas, que contienen el material genético
responsable del funcionamiento celular y de la transmisión de los caracteres que se
heredan. La identiplicación es un proceso aritmético descubierto por Sergio Aschero
que permite conservar el ADN de un número impar a lo largo de todo su desarrollo.
El procedimiento para identiplicar un número impar es el siguiente:
a) Dividir por dos el número impar inicial (generador) de cada serie (1 : 2 = 0,5)
(centro)
b) Sumar el resultado de la división y sumarle a su vez 0,5 (0 + 5 = 5) (5 + 0,5) = 5,5
c) El resultado final multiplicado por dos es el próximo número identiplicado en relación
al número anterior (en este caso 1) (5,5 x 2 = 11)…
Todos los números identiplicados forman parte de las cinco series de números
generadores posibles: 1, 3, 5, 7, 9.
Número generador: 1
1 = 0,5 x 2
11 = 5,5 x 2
21 = 10,5 x 2
31 = 15,5 x 2
41 = 20,5 x 2
51 = 25,5 x 2
21
61 = 30,5 x 2
71 = 35,5 x 2
81 = 40,5 x 2
91 = 45,5 x 2
101 = 50,5 x 2
111 = 55,5 x 2
121 = 60,5 x 2
131 = 65,5 x 2
141 = 70,5 x 2
151 = 75,5 x 2
161 = 80,5 x 2
171 = 85,5 x 2
181 = 90,5 x 2
191 = 95,5 x 2
201 = 100,5 x 2
211 = 105,5 x 2
221 = 110,5 x 2
231 = 115,5 x 2
241 = 120,5 x 2
251 = 125,5 x 2
261 = 130,5 x 2
271 = 135,5 x 2
281 = 140,5 x 2
291 = 145,5 x 2
301 = 150,5 x 2
311 = 155,5 x 2
321 = 160,5 x 2
331 = 165,5 x 2
341 = 170,5 x 2
22
351 = 175,5 x 2
361 = 180,5 x 2
371 = 185,5 x 2
381 = 190,5 x 2
391 = 195,5 x 2
401 = 200,5 x 2
411 = 205,5 x 2
421 = 210,5 x 2
431 = 215,5 x 2
441 = 220,5 x 2
451 = 225,5 x 2
461 = 230,5 x 2
471 = 235,5 x 2
481 = 240,5 x 2
491 = 245,5 x 2
501 = 250,5 x 2
511 = 255,5 x 2
521 = 260,5 x 2
531 = 265,5 x 2
541 = 270,5 x 2
551 = 275,5 x 2
561 = 280,5 x 2
571 = 285,5 x 2
581 = 290,5 x 2
591 = 295,5 x 2
601 = 300,5 x 2
611 = 305,5 x 2
621 = 310,5 x 2
631 = 315,5 x 2
23
641 = 320,5 x 2
651 = 325,5 x 2
661 = 330,5 x 2
671 = 335,5 x 2
681 = 340,5 x 2
691 = 345,5 x 2
701 = 350,5 x 2
711 = 355,5 x 2
721 = 360,5 x 2
731 = 365,5 x 2
741 = 370,5 x 2
751 = 375,5 x 2
761 = 380,5 x 2
771 = 385,5 x 2
781 = 390,5 x 2
791 = 395,5 x 2
801 = 400,5 x 2
811 = 405,5 x 2
821 = 410,5 x 2
831 = 415,5 x 2
841 = 420,5 x 2
851 = 425,5 x 2
861 = 430,5 x 2
871 = 435,5 x 2
881 = 440,5 x 2
891 = 445,5 x 2
901 = 450,5 x 2
911 = 455,5 x 2
921 = 460,5 x 2
24
931 = 465,5 x 2
941 = 470,5 x 2
951 = 475,5 x 2
961 = 480,5 x 2
971 = 485,5 x 2
981 = 490,5 x 2
991 = 495,5 x 2
1001 = 500,5 x 2
Número generador: 3
3 = 1,5 x 2
13 = 6,5 x 2
23 = 11,5 x 2
33 = 16,5 x 2
43 = 21,5 x 2
53 = 26,5 x 2
63 = 31,5 x 2
73 = 36,5 x 2
83 = 41,5 x 2
93 = 46,5 x 2
103 = 51,5 x 2
113 = 56,5 x 2
123 = 61,5 x 2
133 = 66,5 x 2
143 = 71,5 x 2
153 = 76,5 x 2
163 = 81,5 x 2
173 = 86,5 x 2
25
183 = 91,5 x 2
193 = 96,5 x 2
203 = 101,5 x 2
213 = 106,5 x 2
223 = 111,5 x 2
233 = 116,5 x 2
243 = 121,5 x 2
253 = 126,5 x 2
263 = 131,5 x 2
273 = 136,5 x 2
283 = 141,5 x 2
293 = 146,5 x 2
303 = 151,5 x 2
313 = 156,5 x 2
323 = 161,5 x 2
333 = 166,5 x 2
343 = 171,5 x 2
353 = 176,5 x 2
363 = 181,5 x 2
373 = 186,5 x 2
383 = 191,5 x 2
393 = 196,5 x 2
403 = 201,5 x 2
413 = 206,5 x 2
423 = 211,5 x 2
433 = 216,5 x 2
443 = 221,5 x 2
453 = 226,5 x 2
463 = 231,5 x 2
26
473 = 236,5 x 2
483 = 241,5 x 2
493 = 246,5 x 2
503 = 251,5 x 2
513 = 256,5 x 2
523 = 261,5 x 2
533 = 266,5 x 2
543 = 271,5 x 2
553 = 276,5 x 2
563 = 281,5 x 2
573 = 286,5 x 2
583 = 291,5 x 2
593 = 296,5 x 2
603 = 301,5 x 2
613 = 306,5 x 2
623 = 311,5 x 2
633 = 316,5 x 2
643 = 321,5 x 2
653 = 326,5 x 2
663 = 331,5 x 2
673 = 336,5 x 2
683 = 341,5 x 2
693 = 346,5 x 2
703 = 351,5 x 2
713 = 356,5 x 2
723 = 361,5 x 2
733 = 366,5 x 2
743 = 371,5 x 2
753 = 376,5 x 2
27
763 = 381,5 x 2
773 = 386,5 x 2
783 = 391,5 x 2
793 = 396,5 x 2
803 = 401,5 x 2
813 = 406,5 x 2
823 = 411,5 x 2
833 = 416,5 x 2
843 = 421,5 x 2
853 = 426,5 x 2
863 = 431,5 x 2
873 = 436,5 x 2
883 = 441,5 x 2
893 = 446,5 x 2
903 = 451,5 x 2
913 = 456,5 x 2
923 = 461,5 x 2
933 = 466,5 x 2
943 = 471,5 x 2
953 = 476,5 x 2
963 = 481,5 x 2
973 = 486,5 x 2
983 = 491,5 x 2
993 = 496,5 x 2
1003 = 501,5 x 2
Número generador: 5
5 = 2,5 x 2
28
15 = 7,5 x 2
25 = 12,5 x 2
35 = 17,5 x 2
45 = 22,5 x 2
55 = 27,5 x 2
65 = 32,5 x 2
75 = 37,5 x 2
85 = 42,5 x 2
95 = 47,5 x 2
105 = 52,5 x 2
115 = 57,5 x 2
125 = 62,5 x 2
135 = 67,5 x 2
145 = 72,5 x 2
155 = 77,5 x 2
165 = 82,5 x 2
175 = 87,5 x 2
185 = 92,5 x 2
195 = 97,5 x 2
205 = 102,5 x 2
215 = 107,5 x 2
225 = 112,5 x 2
235 = 117,5 x 2
245 = 122,5 x 2
255 = 127,5 x 2
265 = 132,5 x 2
275 = 137,5 x 2
285 = 142,5 x 2
295 = 147,5 x 2
29
305 = 152,5 x 2
315 = 157,5 x 2
325 = 162,5 x 2
335 = 167,5 x 2
345 = 172,5 x 2
355 = 177,5 x 2
365 = 182,5 x 2
375 = 187,5 x 2
385 = 192,5 x 2
395 = 197,5 x 2
405 = 202,5 x 2
415 = 207,5 x 2
425 = 212,5 x 2
435 = 217,5 x 2
445 = 222,5 x 2
455 = 227,5 x 2
465 = 232,5 x 2
475 = 237,5 x 2
485 = 242,5 x 2
495 = 247,5 x 2
505 = 252,5 x 2
515 = 257,5 x 2
525 = 262,5 x 2
535 = 267,5 x 2
545 = 272,5 x 2
555 = 277,5 x 2
565 = 282,5 x 2
575 = 287,5 x 2
585 = 292,5 x 2
30
595 = 297,5 x 2
605 = 302,5 x 2
615 = 307,5 x 2
625 = 312,5 x 2
635 = 317,5 x 2
645 = 322,5 x 2
655 = 327,5 x 2
665 = 332,5 x 2
675 = 337,5 x 2
685 = 342,5 x 2
695 = 347,5 x 2
705 = 352,5 x 2
715 = 357,5 x 2
725 = 362,5 x 2
735 = 367,5 x 2
745 = 372,5 x 2
755 = 377,5 x 2
765 = 382,5 x 2
775 = 387,5 x 2
785 = 392,5 x 2
795 = 397,5 x 2
805 = 402,5 x 2
815 = 407,5 x 2
825 = 412,5 x 2
835 = 417,5 x 2
845 = 422,5 x 2
855 = 427,5 x 2
865 = 432,5 x 2
875 = 437,5 x 2
31
885 = 442,5 x 2
895 = 447,5 x 2
905 = 452,5 x 2
915 = 457,5 x 2
925 = 462,5 x 2
935 = 467,5 x 2
945 = 472,5 x 2
955 = 477,5 x 2
965 = 482,5 x 2
975 = 487,5 x 2
985 = 492,5 x 2
995 = 497,5 x 2
1005 = 502,5 x 2
Número generador: 7
7 = 3,5 x 2
17 = 8,5 x 2
27 = 13,5 x 2
37 = 18,5 x 2
47 = 23,5 x 2
57 = 28,5 x 2
67 = 33,5 x 2
77 = 38,5 x 2
87 = 43,5 x 2
97 = 48,5 x 2
107 = 53,5 x 2
117 = 58,5 x 2
127 = 63,5 x 2
32
137 = 68,5 x 2
147 = 73,5 x 2
157 = 78,5 x 2
167 = 83,5 x 2
177 = 88,5 x 2
187 = 93,5 x 2
197 = 98,5 x 2
207 = 103,5 x 2
217 = 108,5 x 2
227 = 113,5 x 2
237 = 118,5 x 2
247 = 123,5 x 2
257 = 128,5 x 2
267 = 133,5 x 2
277 = 138,5 x 2
287 = 143,5 x 2
297 = 148,5 x 2
307 = 153,5 x 2
317 = 158,5 x 2
327 = 163,5 x 2
337 = 168,5 x 2
347 = 173,5 x 2
357 = 178,5 x 2
367 = 183,5 x 2
377 = 188,5 x 2
387 = 193,5 x 2
397 = 198,5 x 2
407 = 203,5 x 2
417 = 208,5 x 2
33
427 = 213,5 x 2
437 = 218,5 x 2
447 = 223,5 x 2
457 = 228,5 x 2
467 = 233,5 x 2
477 = 238,5 x 2
487 = 243,5 x 2
497 = 248,5 x 2
507 = 253,5 x 2
517 = 258,5 x 2
527 = 263,5 x 2
537 = 268,5 x 2
547 = 273,5 x 2
557 = 278,5 x 2
567 = 283,5 x 2
577 = 288,5 x 2
587 = 293,5 x 2
597 = 298,5 x 2
607 = 303,5 x 2
617 = 308,5 x 2
627 = 313,5 x 2
637 = 318,5 x 2
647 = 323,5 x 2
657 = 328,5 x 2
667 = 333,5 x 2
677 = 338,5 x 2
687 = 343,5 x 2
697 = 348,5 x 2
707 = 353,5 x 2
34
717 = 358,5 x 2
727 = 363,5 x 2
737 = 368,5 x 2
747 = 373,5 x 2
757 = 378,5 x 2
767 = 383,5 x 2
777 = 388,5 x 2
787 = 393,5 x 2
797 = 398,5 x 2
807 = 403,5 x 2
817 = 408,5 x 2
827 = 413,5 x 2
837 = 418,5 x 2
847 = 423,5 x 2
857 = 428,5 x 2
867 = 433,5 x 2
877 = 438,5 x 2
887 = 443,5 x 2
897 = 448,5 x 2
907 = 453,5 x 2
917 = 458,5 x 2
927 = 463,5 x 2
937 = 468,5 x 2
947 = 473,5 x 2
957 = 478,5 x 2
967 = 483,5 x 2
977 = 488,5 x 2
987 = 493,5 x 2
997 = 498,5 x 2
35
1007 = 503,5 x 2
Número generador: 9
9 = 4,5 x 2
19 = 9,5 x 2
29 = 14,5 x 2
39 = 19,5 x 2
49 = 24,5 x 2
59 = 29,5 x 2
69 = 34,5 x 2
79 = 39,5 x 2
89 = 44,5 x 2
99 = 49,5 x 2
109 = 54,5 x 2
119 = 59,5 x 2
129 = 64,5 x 2
139 = 69,5 x 2
149 = 74,5 x 2
159 = 79,5 x 2
169 = 84,5 x 2
179 = 89,5 x 2
189 = 94,5 x 2
199 = 99,5 x 2
209 = 104,5 x 2
219 = 109,5 x 2
229 = 114,5 x 2
239 = 119,5 x 2
249 = 124,5 x 2
36
259 = 129,5 x 2
269 = 134,5 x 2
279 = 139,5 x 2
289 = 144,5 x 2
299 = 149,5 x 2
309 = 154,5 x 2
319 = 159,5 x 2
329 = 164,5 x 2
339 = 169,5 x 2
349 = 174,5 x 2
359 = 179,5 x 2
369 = 184,5 x 2
379 = 189,5 x 2
389 = 194,5 x 2
399 = 199,5 x 2
409 = 204,5 x 2
419 = 209,5 x 2
429 = 214,5 x 2
439 = 219,5 x 2
449 = 224,5 x 2
459 = 229,5 x 2
469 = 234,5 x 2
479 = 239,5 x 2
489 = 244,5 x 2
499 = 249,5 x 2
509 = 254,5 x 2
519 = 259,5 x 2
529 = 264,5 x 2
539 = 269,5 x 2
37
549 = 274,5 x 2
559 = 279,5 x 2
569 = 284,5 x 2
579 = 289,5 x 2
589 = 294,5 x 2
599 = 299,5 x 2
609 = 304,5 x 2
619 = 309,5 x 2
629 = 314,5 x 2
639 = 319,5 x 2
649 = 324,5 x 2
659 = 329,5 x 2
669 = 334,5 x 2
679 = 339,5 x 2
689 = 344,5 x 2
699 = 349,5 x 2
709 = 354,5 x 2
719 = 359,5 x 2
729 = 364,5 x 2
739 = 369,5 x 2
749 = 374,5 x 2
759 = 379,5 x 2
769 = 384,5 x 2
779 = 389,5 x 2
789 = 394,5 x 2
799 = 399,5 x 2
809 = 404,5 x 2
819 = 409,5 x 2
829 = 414,5 x 2
38
839 = 419,5 x 2
849 = 424,5 x 2
859 = 429,5 x 2
869 = 434,5 x 2
879 = 439,5 x 2
889 = 444,5 x 2
899 = 449,5 x 2
909 = 454,5 x 2
919 = 459,5 x 2
929 = 464,5 x 2
939 = 469,5 x 2
949 = 474,5 x 2
959 = 479,5 x 2
969 = 484,5 x 2
979 = 489,5 x 2
989 = 494,5 x 2
999 = 499,5 x 2
1009 = 504,5 x 2
A continuación veamos la Tabla de Identiplicar donde se simplifican los resultados de
la multiplicación y se genera un modelo novedoso de relaciones internumerales.
39
Tabla de identiplicar
1
2
3
4
5
6
7
8
9
10
11
12
1
1
2
3
4
5
6
7
8
9
1
2
3
2
2
4
6
8
1
3
5
7
9
2
4
6
3
3
6
9
3
6
9
3
6
9
3
6
9
4
4
8
3
7
2
6
1
5
9
4
8
3
5
5
1
6
2
7
3
8
4
9
5
1
6
6
6
3
9
6
3
9
6
3
9
6
3
9
7
7
5
3
1
8
6
4
2
9
7
5
3
8
8
7
6
5
4
3
2
1
9
8
7
6
9
9
9
9
9
9
9
9
9
9
9
9
9
10
1
2
3
4
5
6
7
8
9
1
2
3
11
2
4
6
8
1
3
5
7
9
2
4
6
12
3
6
9
3
6
9
3
6
9
3
6
9
Modelo: 1 x 1 = 1
3 x 4 = 12 (1 + 2 = 3) 3 x 4 = 3
(números compuestos puros)
40
4. Modelo decimal
Antes de existir el lenguaje escrito, el hombre primitivo se comunicaba con sus
semejantes gesticulando palabras o sonidos, este medio de lenguaje audible se fue
perfeccionando al cabo de miles de años de su continuo uso, hasta llegar a la palabra
hablada. Cuando éste deseaba recordar un hecho o transmitir un acontecimiento a sus
congéneres, les comunicaba sus ideas por medio de la pictografía. Esta consistía en
representar por medio de objetos lo que se deseaba expresar ayudado del dibujo o la
pintura, de esta manera el hombre inventó su primera forma de comunicación no
hablada, la escritura pictográfica.
Hace unos 6000 años a.C. los fenicios, sumerios y babilonios registraban sus hechos y
acontecimientos por medio de figuras dibujadas en arcilla húmeda, este tipo de
escritura se llamó cuneiforme, o en forma de cuña, porque cada trazo del escrito se
hacía oprimiendo sobre tablillas de arcilla que posteriormente secaban al sol o la
cocían. El trazo representaba el objeto dibujado, posteriormente lo convirtió en un
símbolo relacionado con el mismo objeto, esta etapa de la escritura que el hombre
desarrolló, se le llamó ideográfica.
Los egipcios emplearon una escritura ideográfica que se fue perfeccionando con el
tiempo y recibió el nombre de jeroglífica, este modo de escritura les servía para
realizar sus inscripciones en los templos, tumbas y monumentos.
La escritura ideográfica egipcia tiene dos evoluciones perfectamente definidas, la
primera parte de la evolución de la escritura ideográfica es convertirse en jeroglífica
para acabar en una escritura cursiva con sus dos variedades, la hierática y demótica.
La escritura hierática era una especie de taquigrafía abreviada de los jeroglíficos, muy
usada entre los sacerdotes para expresarse rápidamente al no utilizarse el dibujo,
cada jeroglífico tenía su correspondiente abreviatura hierática, dominando el elemento
fonético y escribiéndose de derecha a izquierda.
La demótica o popular se componía de signos tomados de la hierática, con exclusión
casi completa de los jeroglíficos, conservándose casi completamente los símbolos
cuña de sus caracteres compuestos por ángulos y puntas. La escritura jeroglífica se
utilizaba para las inscripciones monumentales, donde solamente los sacerdotes y los
escribas conocían su significado. En esta escritura jeroglífica se encuentran unos 24
signos alfabéticos equivalentes a letras sueltas o palabras completas separadas de
una sola consonante, 136 signos silábicos, pero al lado de estos se encuentran más
de tres mil figuras mucho más complicadas. Los egipcios nunca advirtieron la
importancia de su magna invención y no hicieron mucho uso de ella.
Aunque se carece de información fidedigna acerca de la forma como el hombre
primitivo empezó a valerse de un sistema numérico, tuvo muchas razones y
situaciones cotidianas que lo impulsaron a tratar de cuantificar todo lo que le rodeaba.
En su etapa sedentaria se vio forzado a emplear algún método de conteo, ya fuera
para saber cuántas cabezas de ganado u ovejas poseía; como también para conocer
el número de armas que tenía, o para cuantificar la extensión de los terrenos
sembrados o conquistados.
41
Nuestros antepasados debieron hacer un gran esfuerzo para alejarse de lo concreto y
la realidad del mundo circundante, para llegar a la concepción de la entidad numérica,
al realizar esta abstracción numérica el hombre partió de la consideración de las
entidades físicas tangibles en su mundo. De esta manera el hombre descubrió el
primer sistema de matemáticas aplicadas, que luego los matemáticos definirían como
una correspondencia biunívoca entre dos órdenes.
También cuando éste se dedicó a la agricultura, tuvo que idear un sistema para medir
el tiempo en las épocas de siembra y cosecha, finalmente en su etapa de comerciante,
necesitó crear un sistema para fijar el peso, volumen y el valor de sus productos para
intercambiarlos con los pueblos vecinos.
Al tener el hombre antiguo un sistema base de medida, se vio en la necesidad de
cuantificar las medidas en su modo base de contar, esta operación la llevó a cabo, por
ejemplo, utilizando un sistema de rayas rasgadas en las paredes o pintadas en papiro;
otro método era haciendo marcas en los troncos de los árboles o cortes sobre una
vara para llevar un registro permanente de las cosas. Cada pueblo o tribu tuvo que
inventar sus propias palabras y signos para representar sus operaciones de conteos
realizados, con el comercio los antiguos mercaderes estaban obligados a saber una
gran variedad de sistemas de medidas y numeración, a fin de poder comerciar con los
diferentes pueblos o tribus.
Para llegar a la concepción e invención de un sistema numérico, fueron necesarios
muchos miles de años antes que el hombre concibiera la idea del número, un paso
fundamental en el proceso de la abstracción matemática fue la creación de los
símbolos matemáticos, las matemáticas es una de las más hermosas creaciones de la
inteligencia de la especie humana, la invención de un sistema numérico es quizá una
de las mayores invenciones del hombre antiguo. Dentro de estos sistemas se
encuentran los aditivos, los híbridos y los posicionales.
Sistemas de numeración aditivos
Este sistema acumula los símbolos de todas las cifras hasta completar el número
deseado, una de sus características es que los símbolos se pueden colocar en
cualquier posición u orden, ya fuera de izquierda a derecha, derecha a izquierda,
arriba hacia abajo, un ejemplo clásico de este sistema es el egipcio, el romano, el
griego.
42
Sistemas de numeración híbridos
Estos sistemas combinan el principio del sistema aditivo con el multiplicativo, pero el
orden en la escritura de las cifras es fundamental para evitar confusiones en su
interpretación, un ejemplo de este sistema es el chino clásico.
Sistemas de numeración posicionales
Es el mejor y más desarrollado sistema inventado por las civilizaciones antiguas, en
ellos la posición de las cifras indica la potencia de la base que le corresponde.
Solamente tres culturas lograron implementar este sistema, la babilónica, la hindú y la
maya, estas dos últimas lograron innovar una nueva cifra de trabajo, el valor posicional
del cero.
Las matemáticas son la ciencia de los fundamentos que trata las estructuras, formas,
magnitudes y relaciones numéricas de configuraciones del pensamiento.
Han sido llamadas correctamente, la reina y sirviente de las ciencias.
A medida que se han desarrollado las matemáticas abstractas, se han intentado
aplicar a ciencias más prácticas, y el cambio de las necesidades científicas ha
motivado la investigación en ciertos campos no tradicionales.
Históricamente, las matemáticas no se han desarrollado como maduración equilibrada
del pensamiento lógico, sino por saltos irregulares e intermitentes, algunas veces con
lagunas de siglos entre avances importantes.
Estos surgen como consecuencia de los estudios efectuados por hombres interesados
en la delimitación de nuevos procesos, y tales hombres aparecen en intervalos no
próximos.
En los primeros tiempos, sólo eran necesarias las más primitivas ideas de aritmética.
Al aparecer el trueque -con los principios de la civilización-, fue necesario aprender
cómo valorar y decir cuántas ovejas se cambiaban por un número de útiles.
Tal vez, cierto número de piedras se amontonaban para significar el valor de una
oveja, y otras se colocaban en un montón diferenciado y representaban el valor de una
cazuela.
Para realizar el cambio de algunas ovejas por otras cosas, seguramente se tomaban
las piedras alternativamente de uno y otro montón (correspondencia de uno a uno), y
43
las que sobraban en un montón, después de haber acabado con el otro, se
negociaban de otra manera.
Este ejemplo intenta ilustrar el uso de las piedras como unidad para materializar el
valor de las cosas, y no habría de pasar mucho tiempo antes de que apareciera una
forma más abstracta de contar (el número).
En un principio para contar, la gente usó los cinco dedos de una mano, y así apareció
la numeración en base cinco.
Hasta hace pocos años este sistema era ampliamente usado en Oriente.
Los ábacos elementales que todavía se encuentran en China y Japón, están
diseñados con este código.
También fue muy utilizado el sistema de numeración romano basado en siete letras.
Es también fácil ver como el diez ha llegado a ser un número importante, motivado
porque el ser humano tiene diez dedos en las manos y diez en los pies.
Las primeras aportaciones tienen miles de años, pero, curiosamente nuestra manera
actual de escribir los números es bastante reciente: utilizada ya por los hindúes, y
difundida por los árabes, no llegó a Europa hasta el siglo XIII.
Durante siglos hubo una verdadera guerra entre los partidarios del sistema literal
romano y del numeral arábigo.
Veamos las diferencias:
Un romano al observar tres rayas verticales trazadas en la arena (durante el imperio
de la antigua Roma), habría entendido que el número representado es tres (III),
mientras que para un romano actual el mismo diseño significaría (111).
Cada uno sigue un código distinto y ambos son coherentes.
Para uno, las tres rayas significan:
1+1+1=3
Y para otro:
100 + 10 + 1 = 111
La gran diferencia entre uno y otro, no está tanto en los signos mismos, como en la
forma de relacionarlos. El romano es aditivo y sustractivo, el arábigo es además
posicional. De allí su poder.
El número es una noción matemática de fundamental importancia, introducida de
manera más o menos consciente desde la antigüedad, con el fin de poder operar
sobre cantidades de elementos que constituyen conjuntos o sobre cantidades que
expresan medidas de entidades materiales.
44
El código decimal presenta algunas deficiencias que empezaremos a señalar:
Si se parte de los diez primeros números (0 a 10) el "centro" es 5.
Sin embargo si avanzamos al siguiente límite (0 a 100) el "centro" es 50, debiendo ser
sin embargo 55. Todos los "centros" tendrían que ser 5, 55, 555…
Para corregir este error hay que producir cambios en el modelo.
El primero tiene que ver con otorgar un símbolo para "el dedo 10" ya que 10 es la
unión del número 1 y del número 0.
A partir de este nuevo modelo decimal de Aschero el cero tradicional se transforma en
el nuevo diez.
45
Si el cero tradicional representa diez, el modelo decimal de Aschero necesita un nuevo
símbolo para representar la nada.
Estos cambios implican una modificación a la hora de contar:
46
Y este es el nuevo sistema de numeración posicional de base diez.
Utiliza las cifras:
1 una unidad
2 dos unidades
3 tres unidades
4 cuatro unidades
5 cinco unidades 0 : 2 = 5 (centro)
6 seis unidades
7 siete unidades
8 ocho unidades
9 nueve unidades
47
0 diez unidades = 1 decena
Opera dando a cada cifra de una secuencia el valor obtenido multiplicando la cifra por
la potencia de 0 relativa a su posición.
Es el más utilizado puesto que permite emplear en los cálculos los dedos de las
manos.
Su origen es indo árabe, fue introducido en Europa por Leonardo de Pisa en el siglo
XIII y modificado para hacerlo realmente decimal por Sergio Aschero a comienzos del
siglo XXI.
Sus decenas se representan así:
11 una decena una unidad
12 una decena dos unidades
13 una decena tres unidades
14 una decena cuatro unidades
15 una decena cinco unidades
16 una decena seis unidades
17 una decena siete unidades
18 una decena ocho unidades
19 una decena nueve unidades
10 una decena diez unidades
21 dos decenas una unidad
22 dos decenas dos unidades
23 dos decenas tres unidades
24 dos decenas cuatro unidades
25 dos decenas cinco unidades
26 dos decenas seis unidades
27 dos decenas siete unidades
28 dos decenas ocho unidades
48
29 dos decenas nueve unidades
20 dos decenas diez unidades
31 tres decenas una unidad
32 tres decenas dos unidades
33 tres decenas tres unidades
34 tres decenas cuatro unidades
35 tres decenas cinco unidades
36 tres decenas seis unidades
37 tres decenas siete unidades
38 tres decenas ocho unidades
39 tres decenas nueve unidades
30 tres decenas diez unidades
41 cuatro decenas una unidad
42 cuatro decenas dos unidades
43 cuatro decenas tres unidades
44 cuatro decenas cuatro unidades
45 cuatro decenas cinco unidades
46 cuatro decenas seis unidades
47 cuatro decenas siete unidades
48 cuatro decenas ocho unidades
49 cuatro decenas nueve unidades
40 cuatro decenas diez unidades
51 cinco decenas una unidad
52 cinco decenas dos unidades
53 cinco decenas tres unidades
54 cinco decenas cuatro unidades
55 cinco decenas cinco unidades 00 : 2 = 55 (centro)
56 cinco decenas seis unidades
57 cinco decenas siete unidades
49
58 cinco decenas ocho unidades
59 cinco decenas nueve unidades
50 cinco decenas diez unidades
61 seis decenas una unidad
62
63
64
65
66
67
68
69
60
71 siete decenas una unidad
72
73
74
75
76
77
78
79
70
81 ocho decenas una unidad
82
83
84
85
86
50
87
88
89
80
91 nueve decenas una unidad
92
93
94
95
96
97
98
99
90
01 diez decenas una unidad
02
03
04
05
06
07
08
09
00 diez decenas diez unidades = 11 una centena una decena
Y sus centenas:
111 una centena una decena una unidad
112
51
113
114
115
116
117
118
119
110
121 una centena dos decenas una unidad
122
123
124
125
126
127
128
129
120
131
132
133
134
135
136
137
138
139
130
141
52
142
143
144
145
146
147
148
149
140
151
152
153
154
155
156
157
158
159
150
161
162
163
164
165
166
167
168
169
160
53
171
172
173
174
175
176
177
178
179
170
181
182
183
184
185
186
187
188
189
180
191
192
193
194
195
196
197
198
199
54
190
101 una centena diez decenas una unidad
102
103
104
105
106
107
108
109
100 una centena diez decenas diez unidades
211 dos centenas una decena una unidad
212
213
214
215
216
217
218
219
210
221
222
223
224
225
226
227
228
55
229
220
231
232
233
234
235
236
237
238
239
230
141
242
243
244
245
246
247
248
249
240
251
252
253
254
255
256
257
56
258
259
250
261
262
263
264
265
266
267
268
269
260
271
272
273
274
275
276
277
278
279
270
281
282
283
284
285
286
57
287
288
289
280
291
292
293
294
295
296
297
298
299
290
201
202
203
204
205
206
207
208
209
200 dos centenas diez decenas diez unidades
311 tres centenas una decena una unidad
312
313
314
315
58
316
317
318
319
310
321
322
323
324
325
326
327
328
329
320
331
332
333
334
335
336
337
338
339
330
341
342
343
344
59
345
346
347
348
349
340
351
352
353
354
355
356
357
358
359
350
361
362
363
364
365
366
367
368
369
360
371
372
373
60
374
375
376
377
378
379
370
381
382
383
384
385
386
387
388
389
380
391
392
393
394
395
396
397
398
399
390
301
302
61
303
304
305
306
307
308
309
300 tres centenas diez decenas diez unidades
411 cuatro centenas una decena una unidad
412
413
414
415
416
417
418
419
410
421
422
423
424
425
426
427
428
429
420
431
62
432
433
434
435
436
437
438
439
430
441
442
443
444
445
446
447
448
449
440
451
452
453
454
455
456
457
458
459
450
63
461
462
463
464
465
466
467
468
469
460
471
472
473
474
475
476
477
478
479
470
481
482
483
484
485
486
487
488
489
64
480
491
492
493
494
495
496
497
498
499
490
401
402
403
404
405
406
407
408
409
400 cuatro centenas diez decenas diez unidades
511 cinco centenas una decena una unidad
512
513
514
515
516
517
518
65
519
510
521
522
523
524
525
526
527
528
529
520
531
532
533
534
535
536
537
538
539
530
541
542
543
544
545
546
547
66
548
549
540
551
552
553
554
555 000 : 2 = 555 (centro)
556
557
558
559
550
561
562
563
564
565
566
567
568
569
560
571
572
573
574
575
576
67
577
578
579
570
581
582
583
584
585
586
587
588
589
580
591
592
593
594
595
596
597
598
599
590
501
502
503
504
505
68
506
507
508
509
500 cinco centenas diez decenas diez unidades
611 seis centenas una decena una unidad
612
613
614
615
616
617
618
619
610
621
622
623
624
625
626
627
628
629
620
631
632
633
634
69
635
636
637
638
639
630
641
642
643
644
645
646
647
648
649
640
651
652
653
654
655
656
657
658
659
650
661
662
663
70
664
665
666
667
668
669
660
671
672
673
674
675
676
677
678
679
670
681
682
683
684
685
686
687
688
689
680
691
692
71
693
694
695
696
697
698
699
690
601
602
603
604
605
606
607
608
609
600 seis centenas diez decenas diez unidades
711 siete centenas una decena una unidad
712
713
714
715
716
717
718
719
710
721
72
722
723
724
725
726
727
728
729
720
731
732
733
734
735
736
737
738
739
730
741
742
743
744
745
746
747
748
749
740
73
751
752
753
754
755
756
757
758
759
750
761
762
763
764
765
766
767
768
769
760
771
772
773
774
775
776
777
778
779
74
770
781
782
783
784
785
786
787
788
789
780
791
792
793
794
795
796
797
798
799
790
701
702
703
704
705
706
707
708
75
709
700 siete centenas diez decenas diez unidades
811 ocho centenas una decena una unidad
812
813
814
815
816
817
818
819
810
821
822
823
824
825
826
827
828
829
820
831
832
833
834
835
836
837
76
838
839
830
841
842
843
844
845
846
847
848
849
840
851
852
853
854
855
856
857
858
859
850
861
862
863
864
865
866
77
867
868
869
860
871
872
873
874
875
876
877
878
879
870
881
882
883
884
885
886
887
888
889
880
891
892
893
894
895
78
896
897
898
899
890
801
802
803
804
805
806
807
808
809
800 ocho centenas diez decenas diez unidades
911 nueve centenas una decena una unidad
912
913
914
915
916
917
918
919
910
921
922
923
924
79
925
926
927
928
929
920
931
932
933
934
935
936
937
938
939
930
941
942
943
944
945
946
947
948
949
940
951
952
953
80
954
955
956
957
958
959
950
961
962
963
964
965
966
967
968
969
960
971
972
973
974
975
976
977
978
979
970
981
982
81
983
984
985
986
987
988
989
980
991
992
993
994
995
996
997
998
999
990
901
902
903
904
905
906
907
908
909
900 nueve centenas diez decenas diez unidades
011 diez centenas una decena una unidad
82
012
013
014
015
016
017
018
019
010
021
022
023
024
025
026
027
028
029
020
031
032
033
034
035
036
037
038
039
030
83
041
042
043
044
045
046
047
048
049
040
051
052
053
054
055
056
057
058
059
050
061
062
063
064
065
066
067
068
069
84
060
071
072
073
074
075
076
077
078
079
070
081
082
083
084
085
086
087
088
089
080
091
092
093
094
095
096
097
098
85
099
090
001
002
003
004
005
006
007
008
009
000 diez centenas diez decenas diez unidades
...........................................................................................................................................
1111 una unidad de millar una centena una decena una unidad
0000 diez millares diez centenas diez decenas diez unidades
11111 una decena de millar una unidad de millar una centena
una decena una unidad
00000 cien millares diez millares diez centenas diez decenas diez unidades
111111 una centena de millar una decena de millar una unidad de millar una
centena una decena una unidad
000000 mil millares cien millares diez millares diez centenas diez decenas diez
unidades
...........................................................................................................................................
1111111 una unidad de millón una centena de millar una decena de millar una
unidad de millar una centena una decena una unidad
...........................................................................................................................................
86
Tipología numeral
a.- Número Abundante
Número natural para el cual, la suma de sus divisores es mayor que su duplo:
12 tiene los divisores 1, 2, 3, 4, 6, 12 y es
1 + 2 + 3 + 4 + 6 + 12 = 28; 28 > 2 : 12.
b.- Números Amigos
Dos números tales que la suma de los divisores de cada uno de ellos es igual al otro
número respectivamente: 284 y 220.
c.- Números de Fibonacci
1, 1, 2, 3, 5, 8, 13, 21, 34...
d.- Números de Pitágoras
32 + 42 = 52
e.- Números de Aschero (nueva serie)
1 + 3 - 2 + 4 - 3 + 5 - 4 + 6...
f.- Números Triangulares
3, 6, 0, 15...
g.- Números Cuadrados
4, 9, 16, 25...
h.- Números Pentagonales
5, 12, 22...
87
i.- Números Pares
2, 4, 6, 8...
j.- Números Impares
1, 3, 5, 7...
k.- Números Opuestos
3/4, -3/4
l.- Números Perfectos
6, 28, 496...
Son iguales a la suma de sus divisores:
28 = 1 + 2 + 4 + 7 + 14
m.- Números Primos
1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89,
97...
n.- Números Racionales
4/3, 2/4
ñ.- Números Binarios
0, 1
o.- Números Naturales
1, 2, 3, 4...
88
p.- Números Ordinales
1º, 2º, 3º...
q.- Números Negativos
-1, -2, -3...
r.- Números Positivos
1, 2, 3, 4...
s.- Números Irracionales y Trascendentes
No son representables como fracción de dos números enteros. Se representan como
fracciones decimales infinitas no periódicas.
π = 3, 1415926536...
e = 2, 71828182284...
t.- Números Enteros
-3, 4, 90...
u.- Números Decimales
1,33
v.- Números Algebraicos
(X - 2)2
w.- Números Imaginarios
5i, 8i...
x.- Números Complejos
3 + 4i = 3 parte real y 4 parte imaginaria
89
Algoritmo
Conjunto bien definido de instrucciones o condiciones operativas que regulan el
comportamiento de un operador para la resolución de un problema.
Período
La repetición de determinados valores numerales en una sucesión.
1:7 = X, 142857 = 142857142857...
Número combinatorio
(8/5) = 8 . 7 . 6 . 5 . 4 : 1 . 2 . 3 . 4 . 5 = 56
Cuadrado mágico
16 3 2 13
5
0 11 8
9
6 7 12
4 15 14 1
Ordenación cuadrada de números enteros, de forma que las sumas por columnas, por
filas y en diagonal coincidan.
Triángulo de Tartaglia
1
1
1
1
1
1 5
1
2
3
4
1
3
6
0
1
4
0
1
5
1
1 6 15 10 15 6 1
90
Paréntesis
a x (b + c) = ab + ac
a x b + c = ab + c
a + b (c + d) = a + bc + bd
a + b (c - d) = a + bc – bd
a - b (c + d) = a - bc - bd
a - b (c - d) = a - bc + bd
Sucesión armónica
1, 1/2, 1/3, 1/4, 1/5, 1/6...
Sucesión convergente
1/2 + 1/4 + 1/8 + 1/16... (menor que 1)
Sucesión divergente
1/2 + 1/3 + 1/4 + 1/5... (mayor que 1)
91
5. El nonúmero
El ser humano ha sido definido como animal simbólico. La definición no puede ser
más certera, pues uno de los rasgos que lo definen y le diferencian del resto de los
animales es su capacidad de simbolización, que empieza con el lenguaje y culmina
con la simbolización de la relación de la persona con el mundo y las cosas. El
símbolo no es algo exclusivo de los niños y niñas, de las personas neuróticas, o de
los pueblos llamados "primitivos". Resulta consustancial al ser humano, constituye
una parte fundamental de su vida espiritual y es anterior al lenguaje y a la razón
discursiva. Ser persona, resumiendo las aportaciones de las principales
antropologías de nuestro siglo, es "simbolizar la existencia".
El ser humano puede representar el mundo de dos maneras: directa e
indirectamente. La directa tiene lugar cuando la cosa se representa "en carne y
hueso" y se hace presente en sí misma. La indirecta sucede cuando el objeto está
ausente y se le representa al ser humano en imagen. Una de esas formas
indirectas de representación es el símbolo.
La palabra "símbolo" proviene del verbo griego symballein, que, en su forma
transitiva, significa poner en común, reunir, intercambiar y, en su forma intransitiva,
encontrarse, juntarse. El sustantivo symbolon significa conjunción, pacto, reunión
de las dos partes en que se dividía el objeto.
El símbolo antiguo indica un objeto que se rompe en dos partes iguales de forma
que cada uno de los firmantes de un pacto se queda con una parte. Cada parte por
separado carece de valor. El valor simbólico radica en la relación de una mitad con
la otra. La unión de ambas partes llevada a cabo por los portadores es lo que
constituye la prenda del pacto. La reunión de las partes escindidas lleva al
reconocimiento, a la identificación y al encuentro.
El mundo de los símbolos constituye un ejercicio de equilibrio entre la herencia
recibida y la creatividad. El ser humano no parte de cero, ni las comunidades
pueden hacer tabla rasa del pasado. Los símbolos no se inventan todos los días,
como tampoco cambian arbitrariamente cual si de productos de moda se tratara.
Perviven por encima de los avatares a los que están expuestos y resisten los
múltiples embates a los que están expuestos. Lo que suele cambiar con el tiempo
no son los símbolos, sino su significado.
El experimento se erige en la única forma de experiencia válida. Todas las esferas
de la vida humana, se modelan de acuerdo con las técnicas del laboratorio. Los
problemas filosóficos se resuelven según los métodos experimentales modernos.
Para el positivismo, las funciones de la filosofía son la clasificación y la
formalización de los métodos científicos. Y cuando la filosofía se resiste a aceptar
esas funciones se la reduce a poesía o mística, y se la coloca despectivamente
junto a la teología. Y cuando sigue firme denunciando con pertinacia y tesón las
prácticas destructivas de la ciencia, se le da como respuesta que la causa de tales
prácticas no está en la naturaleza misma de la ciencia, siempre tan benefactora,
sino en el mal uso que de ella se hace.
¿Se oponen símbolo y razón? ¿Atenta el símbolo contra la razón o ésta contra
aquél? Ésa es una imagen muy extendida de la relación entre uno y otra. Pero no
parece que sea correcta. El símbolo no lucha contra la razón, ni la razón debe
buscar la eliminación del símbolo. El símbolo no es un simple adorno de la razón ni
ejerce una función subsidiaria del concepto. Hay una razón simbólica que amplía el
92
horizonte de la razón achicada por los positivismos y empirismos destructores del
símbolo.
El símbolo libera a la razón moderna de los autoritarismos, absolutismos,
automatismos, utilitarismos e instrumentalizaciones en que ha podido caer bajo el
imperio de los positivismos.
La razón simbólica no pretende dominar, imponer, ni sacar partido; se caracteriza
por la gratuidad, la alteridad y la no-manipulación. Es una razón solidaria, dialógica
y respetuosa con otras formas de racionalidad.
El símbolo representa algo que va más allá de su significado inmediato y del
alcance de la razón. Muchas cosas escapan al alcance del entendimiento humano
y requieren de la mediación del símbolo para su expresión y comunicación.
El símbolo se caracteriza por poseer un plus de sentido. Añade un nuevo valor a
una acción o un objeto, convirtiéndolos en algo abierto que lleva a la profundidad
de lo real. En ese sentido, remite a experiencias, aspiraciones y niveles profundos
de la existencia humana y de la realidad cósmica que no son expresables por la vía
de la razón teórica o del discurso racional, ni encuentran traducción adecuada por
vía conceptual. Éste es el caso de experiencias humanas fundamentales como la
vida, la muerte, el sufrimiento, la alegría, el amor, el miedo, la esperanza, la fe, la
compasión, la reconciliación, el perdón, la fraternidad, la felicidad, la fidelidad, la
confianza. El ser humano recurre a los grandes símbolos que ha tejido la
humanidad en su historia y prehistoria y que están presentes en las diferentes
culturas y religiones para expresar esas experiencias: el agua, el aire, el fuego, la
tierra, el cielo, el abismo, el árbol, la luz, el sol, los miedos, el camino, el éxodo,
animales, plantas, constelaciones, etc.
El símbolo viene a constituir una especie de puente que relaciona dos sentidos: el
literal y aquel al que remite el literal. La relación entre ambos sentidos es profunda
e interna. A diferencia del signo, que remite a algo distinto de sí mismo, el símbolo
nos introduce en el orden cultural, ritual y cultural, del que él mismo forma parte. El
significante tiene que ver con el significado.
El símbolo determina una ausencia y actualiza algo que no puede alcanzarse, que
es imposible de percibir o no es conocido. El símbolo nos abre a la trascendencia
en el seno de la inmanencia, apunta a la presencia en medio de la ausencia, remite
a la comunicación cuando se experimenta la soledad. Pero precisamente por su
carácter inabarcable, el símbolo, además de desvelar, vela, además de manifestar,
oculta, para no disolver el misterio.
El símbolo realiza aquello a lo que remite: el silencio o el pésame en un duelo
constituyen una presencialización del acompañamiento y de la solidaridad en el
dolor; un efusivo apretón de manos expresa la amistad con la persona a quien se
dirige; un beso es un signo de afecto y cariño. Pero la presencia de esos
sentimientos a través de los símbolos referidos no agota su significado profundo.
Dadas la riqueza y profundidad de los símbolos, hay siempre un fondo al que nunca
se llega ni puede expresarse.
La riqueza y profundidad del símbolo muestran otro elemento fundamental: la
variedad y pluralidad de significaciones. El mismo símbolo no posee un solo
significado, sino que remite a múltiples significados.
93
El campo simbólico no se queda en los objetos, se amplía a las palabras, los
gestos, las personas, los animales y lo desconocido, etc.
Suele ser muy corriente oponer símbolo a realidad. Pero tal oposición no tiene por
qué darse. El símbolo afecta a lo más real y profundo de la persona y de su mundo.
Así, por ejemplo, en un duelo, sobran las palabras y son sustituidas por multitud de
símbolos: una corona de flores, el silencio y/o el beso de condolencia, las lágrimas
de solidaridad. Estos y otros símbolos pretenden expresar la presencia solidaria, la
comunicación entre dos sujetos, la alteridad compartida.
No es válida, por tanto, la disyuntiva: símbolo o realidad, simbólico o histórico, ni
son acertadas expresiones como "cuanto más simbólico, menos real" o "cuanto
más simbólico, menos importante". Lo simbólico no implica negación de lo histórico,
ni excluye lo histórico. Lo simbólico es independiente de lo histórico, pero no lo
sustituye. Lo que hace es enraizar lo histórico en lo real.
La tendencia innata del ser humano en su individualidad es a alterar continuamente
las creencias. La tendencia innata del ser humano como ser social es la
materialización, la coherencia de las creencias. He aquí la verdadera dualidad que
es fuente del desarrollo. Si la humanidad llegase alguna vez al conocimiento de la
verdad "absoluta" (en realidad a un acuerdo general), comenzaría de inmediato a
negarlo.
La negación, como tantas otras estrategias de afrontamiento, no puede calificarse
como inherentemente buena o mala. Debe tenerse en cuenta el contexto y sobre
todo desarrollar principios que especifiquen las condiciones bajo las cuales los
procesos de negación pueden tener consecuencias favorables o desfavorables.
En el intercambio de los bienes operan dos lógicas diferentes: la del valor, que se
centra en los objetos como tales, y la del intercambio simbólico, que se centra en la
relación entre sujetos. De ambas lógicas la que rige en el símbolo es la segunda. El
símbolo escapa a todo esquema de valor, a toda concepción utilitarista y
productivista de la vida y del ser humano. No se mueve en el marco del valor
mercantil ni del valor de uso del objeto. Un regalo sin apenas valor puede resultar
más estimado que un regalo de coste muy elevado. En la esencia del símbolo está
el carecer de valor venal. Lo que importa no es el valor, ni la utilidad social o
económica, sino la comunicación entre los sujetos. Ese es precisamente el
significado originario del concepto "símbolo".
La práctica simbólica no se diluye en otras prácticas humanas, como la política, la
social, la ética, etc. Se rige por su propia gramática y tiene sus propias reglas de
juego. Pero tampoco es independiente de ellas, ni camina en paralelo a las
prácticas referidas, sino que debe articularse con ellas, sin confundirse.
La praxis simbólica tiene una significación liberadora y ejerce una función
humanizadora. Pero, al no contar con defensas ni propias ni ajenas, puede ser
objeto de perversión, manipulación y secuestro ideológico. El poder dominante
tiende a usar y abusar del símbolo, poniéndolo al servicio de sus intereses y
convirtiéndolo en instrumento de alienación de las conciencias y de los colectivos
humanos. De ahí la necesidad de adoptar una actitud vigilante frente a los intentos
varios de manipulación.
Una última característica del símbolo es su carácter comunitario. El símbolo no es
creación individual; precede al individuo, nace en el seno de una colectividad, de
94
ella se nutre y en ella adquiere sentido. El ser humano, simbolizador como es, "no
fabrica los símbolos a su arbitrio, ni entra a su arbitrio en los símbolos
colectivamente generados, para viajar por la vida como se viaja en un utilitario...
Pueden cultivarse como los árboles y morir o secarse si se les arranca de la tierra
las raíces, pero tienen su ritmo de vida y les gusta el aire y el sol de lo natural".
Del carácter comunitario del símbolo emana directamente la participación en él. El
símbolo no es para contemplarlo desde fuera cual espectador pasivo y ajeno; hay
que entrar en su dinámica. El símbolo no se comprende sólo -ni quizá
principalmente- con la cabeza, sino en la medida en que todo el ser humano se
implica en él. Hay una relación bidireccional entre los símbolos y el ser humano.
Éste entra de lleno en el mundo de los símbolos que él mismo ha creado, los recrea
y los abre a nuevos sentidos, compaginando la herencia simbólica recibida y la
nueva simbólica emergente. A su vez, el símbolo es revelador del ser humano.
Las cosas no son una tabla rasa. El símbolo contribuye a mostrar que el
encefalograma de la realidad no es plano; detecta un sentido en ella y es
transmisor de ese sentido. Más aún, las cosas pueden llegar a convertirse en
símbolos gracias al ser humano, que, como vimos al principio, es un animal
simbolizador.
En su relación con el mundo, la primera reacción de la persona es de admiración y
sorpresa. Después, penetra en las cosas y las analiza, intentando establecer las
relaciones de causa a efecto y mutando la admiración por afirmaciones fundadas.
Es el paso de la sorpresa al dominio y a la explicación del mundo, que da lugar a la
ciencia. Además de explicar los fenómenos, el ser humano los sitúa dentro de un
conjunto más amplio. En un tercer momento, los objetos entran en el mundo de la
persona y adquieren contornos humanos, cobran interioridad y trascienden el
carácter objetual de las cosas, que se convierten así en símbolos reveladores de la
interioridad de sí mismas y del ser humano. El símbolo añade un nuevo "valor" a un
objeto o una acción, convirtiéndolos en "algo abierto".
El pensamiento empírico mira al conocimiento explicativo del mundo exterior,
objetivo; en tanto que el pensamiento simbólico tiende a la participación subjetiva
en la intimidad del mundo. Uno y otro plasman orientaciones heteróclitas
(diferentes); no es uno verdadero y otro falso; simplemente hay que reconocer al
pensamiento simbólico y mítico como un pensamiento diferente, profundamente
humano, con derecho a un estatuto propio en una teoría general del conocimiento...
Mientras que la ciencia explica, con su estrategia positivista y establece lo que
puede o no puede ser empíricamente, el pensar mítico tiene carácter valorativo o
delibera y selecciona fines posibles, calibra lo que debe o no debe ser, es decir, lo
que tiene sentido. Cada línea de pensamiento, por su parte, en contraste con la
otra, cobrará conciencia de su parcialidad constitutiva, así como de los peculiares
riesgos de irracionalismo que no son patrimonio exclusivo de la mitología. La
racionalidad puede derivar en racionalización dogmática, como la mitología en
fanatismo: dos formas de lo irracional ante lo que tanto el mito como la razón
científica han de precaverse.
El desafío radica en armonizar tradición y renovación en el mundo de los símbolos.
La fidelidad a la tradición responde a la radicación del ser humano en el tiempo y al
profundo arraigo de los símbolos en la historia anterior. La renovación responde
también al carácter histórico de la persona, que no se queda anclada en el pasado,
sino que vive experiencias nuevas en el presente y recrea su mundo cultural.
95
En lógica y matemática, la negación, también llamada complemento lógico, es
una operación sobre proposiciones, valores de verdad, o en general, valores
semánticos. Intuitivamente, la negación de una proposición es verdadera cuando dicha
proposición es falsa, y viceversa. En lógica clásica la negación está normalmente
identificada con la función de verdad que cambia su valor de verdadero a falso y
viceversa.
La negación clásica es una operación sobre un valor de verdad, típicamente, el valor
de una proposición, que produce un valor de verdadero cuando su operando es falso,
y un valor de falso cuando su operando es verdadero.
La negación de una proposición p se denota de diferentes maneras en varios
contextos de discusión y campos de aplicación. Entre estas variantes, tenemos las
siguientes:
Notación Significado
no p
no p
no p
En lógica, la lógica proposicional es un sistema formal diseñado para analizar ciertos
tipos de argumentos. En lógica proposicional, las fórmulas
representan proposiciones y las conectivas lógicas son operaciones sobre dichas
fórmulas, capaces de formar otras fórmulas de mayor complejidad. Como otros
sistemas lógicos, la lógica proposicional intenta esclarecer nuestra comprensión de la
noción de consecuencia lógica para el rango de argumentos que analiza.
La maquinaria de la lógica proposicional permite formalizar y teorizar sobre la validez
de una gran cantidad de argumentos. Sin embargo, también existen argumentos que
son intuitivamente válidos, pero cuya validez no puede ser probada por la lógica
proposicional.
El alfabeto de un sistema formal es el conjunto de símbolos que pertenecen al
lenguaje del sistema.
Una vez definido el alfabeto, el siguiente paso es determinar qué combinaciones de
símbolos pertenecen al lenguaje del sistema. Esto se logra mediante una gramática
formal. La misma consiste en un conjunto de reglas que definen recursivamente
las cadenas de caracteres que pertenecen al lenguaje. A las cadenas de caracteres
construidas según estas reglas se las llama fórmulas bien formadas.
96
La matemática tiene su sistema simbólico y ese sistema permite desde la lógica
incorporar nuevas variables. Ese el caso del nonúmero de Sergio Aschero.
El nonúmero es la ausencia del número, operador o conjunto que representa y la
presencia de todos los demás números, operadores o conjuntos.
El símbolo que lo identifica es
Veamos algunos ejemplos con no dos:
P (no primos) (En este caso no se opera con ningún número primo)
N (no naturales) (En este caso no se opera con ningún número natural)
97
6. Números armónicos inmanentes
A través de los peldaños móviles de una escalera y el plano inclinado de un tobogán,
podemos situar todos los procesos culturales de la música en cuanto a la organización
modal y tonal de sus sonidos, (aquí cabe reseñar la cuota de sacrificio histórico
necesario en busca del mejor sistema).
La heptafonía es un ordenamiento escalar selectivo (Bach), y el cromatismo, una cierta
aproximación al tobogán totalizador (Wagner).
Entre los cantos de recolección monofónicos de los alacalufes del sur de Chile y los de
fecundación tetrafónicos de los bosquimanos; así como entre los cuartetos de
Beethoven y los de Bartók, existe algo en común: el respeto a una unidad generadora
de lo sonoro, (la matriz universal de toda serie), que permite el desarrollo natural de
cualquier modelo de afinación que, aunque en lo musical no está presente, siempre se
ha deseado encontrar o justificar en los diversos modelos establecidos: la Edad Media
fue la del armónico 3, el Renacimiento llegó hasta el armónico 5, el Barroco y el
Clasicismo hasta el 7 y el 9, y el Romanticismo con Wagner a la cabeza hasta el 12.
Eso es todo y eso es poco.
Supone una aproximación muy lenta hacia la verdadera naturaleza del sonido, que se
frena en gran medida por las propias contradicciones del propio lenguaje musical que
posee en sus genes la base de su propia inoperancia.
No se puede actuar con seriedad en una investigación de este tipo teniendo en cuenta
los modelos admitidos por una cultura decadente por más bellos que nos parezcan.
Nosotros también estamos condicionados por un modelo que nos ha privado de la
riqueza de lo verdaderamente armónico.
Nuestros gustos son poco confiables.
Se debe iniciar la aventura partiendo de un profundo conocimiento de la realidad
sonora y de sus leyes inmutables, que determinan sin excepciones, las reglas
objetivas del lenguaje.
La pérdida de ese supuesto implica la desintegración de los sistemas: la tonalidad
surge de un cierto respeto a sus normas, el atonalismo de su ignorancia.
Cada vez que se ha intentado suplantar la tonalidad, la sensibilidad colectiva ha
rechazado la opción, (el fracaso del dodecafonismo lo testimonia); pero lo curioso es
que Arnold Schönberg intentó crear una falsa naturaleza a través de su concepto serial
- y si bien la naturaleza del sonido es serial, no es menos cierto que es también
supratonal - (un estado de máxima tonalidad) - y eso Schönberg no lo tuvo en cuenta a
la hora de diseñar su propuesta, quedándose sólo en el terreno de lo combinatorio.
Confiesa su incapacidad para hacer de lo natural un lenguaje, (aunque intuye que es
el futuro de la música: "Armonía"), pero su discurso sigue siendo un híbrido
descentrado entre la tradición y el futuro.
Música y naturaleza no comparten los mismos principios.
98
Numerofonía y naturaleza, sí.
Tolomeo y Galileo tampoco compartieron el mismo concepto del universo.
Vivimos de aproximaciones tratando de identificarnos con la totalidad.
"Un auténtico sistema debe ante todo, poseer unas bases que abarquen todos los resultados
que existen realmente, ni uno mas ni uno menos.
Tales bases son las leyes naturales.
Y sólo esas bases, que no tienen excepciones, podrían tener la exigencia de ser
válidas para siempre".
Arnold Schönberg
(Salzburgo, 1921)
La naturaleza unitaria (y desafinada) de la música, no puede describir la realidad
compleja de un sonido armónico por más que se intente representarlo en un espacio
equivocado y por medios que no lo definen.
Los músicos leen las hojas de los libros, los numerofonistas, el libro entero.
El todo es un concepto original que no se resuelve por la suma de alguna de sus
partes.
El número es una noción matemática de fundamental importancia, introducida de
manera más o menos consciente desde la antigüedad, con el fin de poder operar
sobre cantidades de elementos que constituyen conjuntos o sobre cantidades que
expresan medidas de entidades materiales.
La armonía puede entenderse como el equilibrio y la proporción entre las partes de un
todo. En la física, se entiende como armónica una componente sinusoidal de una onda
periódica cuya frecuencia es múltiplo de la otra componente de onda denominada
fundamental.
Un número inmanente es un tipo de número racional que siempre en su esencia (y no
en su apariencia) es igual a sí mismo.
Un número trascendente es un tipo de número irracional que no es raíz de
ningún polinomio (no nulo) con coeficientes enteros (o racionales).
Lo inmanente es esencial y permanente en un ser o en una cosa y no se puede
separar de él por formar parte de su naturaleza y no depender de algo externo.
La inmanencia es el ente intrínseco de un cuerpo; en filosofía se califica a toda aquella
actividad como inmanente a un ser cuando la acción perdura en su interior, cuando
tiene su fin en ese mismo ser. Se opone por lo tanto a trascendencia.
Se llama serie armónica o escala de resonancia superior de un sonido puro de
frecuencia "n", a la sucesión de sonidos puros cuyas frecuencias son múltiplos enteros
de la frecuencia de "n" (2n, 3n, 4n...).
99
El sonido de frecuencia "n" se llama fundamental o primer armónico de la serie y los
demás sonidos de la sucesión se llamarán armónicos, designándose por orden:
segundo armónico, tercer armónico, etc.
Conociendo la frecuencia de "n", bastará conocer el número de orden de un armónico
para deducir su frecuencia.
La serie armónica es teóricamente infinita.
Los armónicos se oyen en razón inversa al cuadrado de su distancia o sea el número
que los representa.
La intensidad del sonido de los armónicos disminuye a medida que se alejan del
sonido fundamental, de tal modo que el armónico 2 se oirá 4 veces menos que el
armónico 1; el armónico 3 se oirá 9 veces menos que el armónico 1; el armónico 8, 64
veces menos que el 1, etc.
Los ocho primeros armónicos (sin contar el séptimo) dan origen a los teoremas de
Tyndall y Helmholtz.
Veamos algunas de las contradicciones del lenguaje musical con respecto a su
relación con los armónicos naturales:
1.- La música se basa en un comportamiento artificioso del sonido.
La escala mayor las notas fa y la no están contenidas en la serie armónica.
Como la notación musical no posee signos propios para representar todos los sonidos
naturales, por su propia configuración histórica y no científica, ni una teoría coherente
para explicarlos; ha ido buscando aproximaciones artificiosas para poder justificar su
escala mayor.
Los sonidos 7, 11, 13 y 14 son de escritura aproximada.
2.- Comete errores físicos y matemáticos.
El armónico 7, (evitado por el piano con la anulación de su sistema vibratorio), impone
su realidad con más fuerza que los teoremas de Tyndall y Helmohltz, y existe a pesar
de ellos.
Tampoco Pitágoras con sus quintas encadenadas pudo cerrar lo que la naturaleza no
cierra.
El mi sostenido de la sexta octava no es igual que el fa de la séptima octava (ese
intervalo de diferencia se denomina: comma pitagórica).
3.- Prohíbe o defiende fuera de toda lógica.
La cuarta aumentada denominada por los teóricos "diabolus in musica" es un intervalo
natural repudiado.
Lo mismo ocurre con las octavas y quintas paralelas, definidas entre los grados 1, 2 y
3 de cada serie.
100
La teoría defiende la existencia del modo menor como fruto de esa naturaleza antes
marginada, y eso es falso.
El modo mayor se forma naturalmente entre los armónicos 4, 5 y 6.
Sin embargo el modo menor es artificial ya que el mi bemol no aparece en la serie
armónica.
4.- Se escuda en la sinrazón de un temperamento inarmónico.
Do = 261,625 Hz.
Do# (Reb) = 277,182 Hz.
Re = 293,664 Hz.
Re# (Mib) = 311,126 Hz.
Mi = 329,627 Hz.
Fa = 349,228 Hz.
Fa# (Solb) = 369,994 Hz.
Sol = 391,995 Hz.
Sol# (Lab) = 415,304 Hz.
La = 440,000 Hz. (diapasón)
La# (Sib) = 466,163 Hz.
Si = 493,883 Hz.
Do’ = 523,250 Hz.
La armonía sólo admite frecuencias de números enteros, siendo los decimales el
origen de la inarmonía.
La única y curiosa excepción la constituye la naturalidad del diapasón (440Hz.)
Una base matemáticamente incorrecta (12) y una escritura anacrónica no pueden
contener la naturaleza expansiva de los armónicos.
Tal como se ha visto, para obtener un resultado armónico, hay que partir de la propia
naturaleza del sonido. Todas las bases musicales 7, 12, 24, 36, 48... (temperadas o
no), pueden ser útiles instrumentalmente pero resultan absolutamente inarmónicas
en mayor o menor grado. Sólo las bases en cuyas frecuencias no existen decimales y
que responden a 2n como eje de su desarrollo serial (2, 4, 8, 16, 32, 64, 128, 256,
512,...), pertenecen a la naturaleza y no son discrepantes.
También en el desarrollo de un embrión, el óvulo fecundado comienza a dividirse y el
número de células empieza a crecer: 1, 2, 4, 8, 16, 32, 64, etc. Éste es un crecimiento
exponencial. Pero el feto sólo puede crecer hasta un tamaño que el útero pueda
101
soportar; así, otros factores comienzan a disminuir el incremento del número de
células, y la tasa de crecimiento disminuye. Después de un tiempo, el niño nace y
continúa creciendo. Finalmente, el número de células se estabiliza y la estatura del
individuo se hace constante. Se ha alcanzado la madurez, en la que el crecimiento se
detiene. En el caso de los gemelos monocigóticos, en cambio, los dos tienen el mismo
origen: un solo óvulo fecundado por un solo espermatozoide. Lo que sucede es que
después de haberse fusionado el material genético de la madre con el del padre, la
célula resultante (conocida como cigoto) se divide muy tempranamente en dos. Los
dos cigotos resultantes quedan con la misma carga genética y por eso que los bebés
terminan siendo idénticos.
Mediante cualquiera de dichas bases y partiendo de la serie armónica, se demuestra
que primero (1º) es el único grado que en todas sus frecuencias produce la "Ley de
Aschero" que señala que el único grado que multiplicado por sí mismo es igual a sí
mismo es primero (1º) con lo que se fundamenta su preponderancia frente a todos los
demás grados de cualquier serie. Cada nuevo Número Armónico Inmanente "suena"
siempre al doble de la frecuencia del anterior desde 1 Hz. hasta el infinito. Estos
números en realidad son siempre un 1 fecundado (que alumbra un 2) y en su
replicación binaria nunca pierde su identidad inicial.
(2 + 2 = 4), (2 x 4 = 8)
(4 x 2 = 8 = 4 = 2 = 1)
(6 x 3 = 18 ≠ 12 = 6 = 3)
102
(5 x 5 = 25 ≠ 20 = 10 = 5), etc.
A partir de aquí se inicia la definición de los Números Armónicos Inmanentes con sus
características particulares y su vinculación con la naturaleza del sonido.
Todos los Números Armónicos Inmanentes se generan multiplicando por dos todos los
productos generados a partir de la operación inicial: 1 x 2 = 2.
103
104
Características:
105
a) Todos los primos armónicos nacen del número 1 y su "replicación celular."
b) La multiplicación de dos primos armónicos da como resultado otro primo
armónico:
8 x 4 = 32, 8 x 128 = 1024…
Modelo
1
2
4
8
16
32
64
128
256
512
1024
2048
4096
8192
16384
32768
65536
131072…
Los armónicos negativos se "crean" en La Ilustración (siglo XVIII), con la intención de
justificar el acorde menor. Se trataba de una abstracción matemática de este acorde
mediante la inversión en espejo de los armónicos postivos (mientras que los positivos
son ascendentes los negativos descienden). Gracias a este tipo de armónicos se
consigue explicar el IV grado.
Su creador fue Zarlino que consideraba que la tercera menor era el intervalo fundador
de la armonía. Anteriormente, Aristoxeno (siglo IV a.C.) instauró la escala de 8 notas
basándose en las proporciones físicas y no matemáticas de los sonidos. También el
francés Rameau, inventó la armonía, es decir, nombró los acordes según los grados y
106
los situó con un orden dentro de la tonalidad, estableciendo la serie armónica
(positiva).
Las frecuencias subarmónicas son frecuencias que están por debajo de la frecuencia
fundamental., existen en la naturaleza y son un problema en el diseño de circuitos
eléctricos.
Por ejemplo, si la frecuencia fundamental de un oscilador son 440 Hz, los
subarmónicos corresponden a 220 Hz. (1/2) y 110 Hz. (1/4) y 55 Hz. (1/8).
La nota sol de la cuarta cuerda es la nota más grave que sale de un violín afinado. O
eso pensaría cualquiera antes de escuchar a la concertista Kimura. Todos los
instrumentos de cuerda tienen en teoría (insisto, en teoría) la posibilidad de tocar notas
todo lo agudas que se quiera. Para subir una octava completa basta con presionar de
forma que la cuerda que vibra reduzca a la mitad su longitud. Una octava más es
volver a reducir a la mitad, y así sucesivamente hasta la paradoja de Zenón. En la
práctica llega un momento que simplemente la cuerda no vibra por razones de
composición y grosor. Luego hay un límite superior por razones físicas.
El límite inferior, sin embargo tiene un fundamento físico-matemático. Por ejemplo,
decíamos que la nota más grave que da un violín es un sol en su cuerda más gruesa.
Para obtener esta nota basta con hacer vibrar la cuerda sin pulsar sobre el mástil.
Cuanto más larga sea la cuerda, más grave será la nota. Pero evidentemente, si bien
podemos pulsar para acortar una cuerda, no existe forma de alargarla. Esa es la limitación
física de los graves.
La limitación matemática es universal: no se podrá emitir una onda que tenga una
longitud de onda más grande que el objeto que la emite. Recordemos que la longitud
de una onda sonora está asociada con lo aguda o grave que es (cuanto más larga,
más grave). Por eso los violines emiten ondas de 30 o 40 centímetros, y el contrabajo
las emite de más de 1 metro. Por eso un bebé nunca podrá cantar como un bajo o
barítono en un coro. Lo mismo ocurre, por ejemplo, con el campo electromagnético:
una antena solo emite ondas electromagnéticas que son como mucho del tamaño de
la propia antena.
Si en lugar de pulsar la cuerda a la mitad, la cuarta parte, etc. (octavas superiores,
agudas) se apoya suavemente el dedo sobre la mitad, la cuarta parte, etc., lo que se
obtiene es un armónico. Podemos decir que lo que Kimura obtiene para sacar del
violín las octavas inferiores son subarmónicos. Cualquiera que no estuviera avisado
diría que su pieza "Capricho para el segundo subarmónico" la tocan dos instrumentos
(violín y violoncello). ¿Pero cómo lo hace?
Su respuesta nos deja, si cabe, más sorprendidos: "En realidad no sé qué es lo que
hago" dice la violinista, que afirma que obtuvo el sonido a base de "prueba y error".
Varios científicos de instituciones americanas y japonesas han intentado abordar el
fenómeno, pero han abandonado tras varias pruebas. Sin embargo, el equipo de
Alfred Hanssen de la Universidad de Tromsø en Noruega ha adquirido un compromiso
más a largo plazo. La apuesta va por el camino de que Kimura desliza su arco sobre
las cuerdas según un comportamiento que en física llamamos no-lineal, dirigido y
amortiguado. Pertenece a esa parte de la ciencia tan joven (los sistemas no lineales)
en la que la respuesta no siempre es proporcional al estímulo, sino que tiene un
107
comportamiento más bien complejo que requiere de métodos que todavía se están
descubriendo.
Sergio Aschero a través de su Matriz de los Números descubre el mundo subarmónico
de los números enteros de la siguiente forma:
Cada número en su matriz tiene un ADN subarmónico que lo acompaña siempre y que
es su huella indeleble en cualquier vínculo con los otros números.
Por supuesto que estas "frecuencias inaudibles" configuran a cada número
otorgándole un "subtimbre" característico. La única frecuencia sin subarmónicos es 1
Hz.
Veamos como:
1 Hz.
2 Hz. = 1 Hz. 1 Hz. (11)
3 Hz. = 1 Hz. 2 Hz. (12, 21)
4 Hz. = 1 Hz. 3 Hz., 2 Hz. 2 Hz. (13, 22, 31)
5 Hz. = 1Hz. 4 Hz., 2 Hz. 3 Hz. (14, 23, 32, 41)
6 Hz. = 1 Hz. 5 Hz., 2 Hz. 4 Hz., 3 Hz. 3 Hz. (15, 24, 33, 42, 51)
7 Hz. = 1 Hz. 6 Hz., 2 Hz. 5 Hz., 3 Hz. 4 Hz. (16, 25, 34, 43, 52, 61)
8 Hz. = 1 Hz. 7 Hz., 2 Hz. 6 Hz., 3 Hz. 5 Hz., 4 Hz. 4 Hz. (17, 26, 35, 44, 53, 62, 71)
9 Hz. = 1 Hz. 8 Hz., 2 Hz. 7 Hz., 3 Hz. 6 Hz., 4 Hz. 5 Hz. (18, 27, 36, 45, 54, 63, 72,
81)
10 Hz. = 1 Hz. 9 Hz., 2 Hz. 8 Hz., 3 Hz. 7 Hz., 4 Hz.6 Hz., 5 Hz. 5 Hz. (19, 28, 37, 46,
55, 64, 73, 82, 91)
11 Hz. = 1 Hz. 10 Hz., 2 Hz. 9 Hz., 3 Hz. 8 Hz., 4 Hz. 7 Hz., 5 Hz. 6 Hz. (110, 29, 38,
47, 56, 65, 74, 83, 92, 101)
12 Hz. = 1 Hz. 11 Hz., 2 Hz. 10 Hz., 3 Hz. 9 Hz., 4 Hz. 8 Hz., 5 Hz. 7 Hz., 6 Hz. 6 Hz.
(111, 210, 39, 48, 57, 66, 75, 84, 93, 102, 111)
13 Hz. = 1 Hz. 12 Hz., 2 Hz. 11 Hz., 3 Hz. 10 Hz., 4 Hz. 9 Hz., 5 Hz. 8 Hz., 6 Hz. 7 Hz.
(112, 211, 310, 49, 58, 67, 76, 85, 94, 103, 112, 121)
14 Hz. = 1 Hz. 13 Hz., 2 Hz. 12 Hz., 3 Hz. 11 Hz., 4 Hz. 10 Hz., 5 Hz. 9 Hz., 6 Hz. 8
Hz., 7 Hz. 7 Hz. (113, 212, 311, 410, 59, 68, 77, 86, 95, 104, 113, 122, 131)
15 Hz. = 1 Hz. 14 Hz., 2 Hz. 13 Hz., 3 Hz. 12 Hz., 4 Hz. 11 Hz., 5 Hz. 10 Hz., 6 Hz. 9
Hz., 7 Hz. 8 Hz. (114, 213, 312, 411, 510, 69, 78, 87, 96, 105, 114, 123, 132, 141)
108
16 Hz. = 1 Hz. 15 Hz., 2 Hz. 14 Hz., 3 Hz. 13 Hz., 4 Hz. 12 Hz., 5 Hz. 11 Hz., 6 Hz. 10
Hz., 7 Hz. 9 Hz., 8 Hz. 8 Hz. (16 Hz. umbral auditivo) (115, 214, 313, 412, 511, 610,
79, 88, 97, 106, 115, 124, 133, 142, 151)…
32 Hz. = 1 Hz. 31 Hz., 2 Hz. 30 Hz., 3 Hz. 29 Hz., 4 Hz. 28 Hz., 5 Hz. 27 Hz., 6 Hz. 26
Hz., 7 Hz. 25 Hz., 8 Hz. 24 Hz., 9 Hz. 23 Hz., 10 Hz. 22 Hz., 11 Hz. 21 Hz., 12 Hz.
20 Hz., 13 Hz. 19 Hz., 14 Hz. 18 Hz., 15 Hz. 17 Hz., 16 Hz. 16 Hz. (131, 230, 329, 428,
527, 626, 725, 824, 923, 1022, 1121, 1220, 1319, 1418, 1517, 1616, 1715, 1814, 1913,
2012, 2111, 2210, 239, 248, 257, 266, 275, 284, 293, 302, 311)…
Los subarmónicos que están dentro de cada frecuencia fundamental definen de forma
categórica el subtimbre de cada una, es decir su esqueleto, sus órganos y sus
funciones; mientras que los armónicos superiores que actúan en lo externo del cuerpo
numérico le otorgan su encarnadura tímbrica que sí puede ser variable.
109
7. Polisuma entrecruzada
En todo número impar elevado al cuadrado y escrito cifra por cifra desde el 1 hasta el
número resultante de dicho cuadrado, estando dichos números ordenados en tantas
líneas como el cuadrado indique, la polisuma entrecruzada establece cuatro
direcciones de lectura que parten del a) (número diagonal izquierdo superior al número
diagonal derecho inferior), b) (del número vertical central superior al número vertical
central inferior), c) (del número diagonal derecho superior al número diagonal izquierdo
inferior) y d) (del número horizontal central izquierdo al número horizontal central
derecho) que sumados independientemente en sus cuatro variables darán el mismo
resultado.
Símbolo de la polisuma entrecruzada:
32
= 15
Fórmula de la polisuma entrecruzada:
n x 3 (n2 + 1) / 2 (fórmula de la polisuma entrecruzada)
32
= 15
3 x (9 + 1) / 2 = 15
1 + 5 + 9 = 15
3 + 5 + 7 = 15
2 + 5 + 8 = 15
4 + 5 + 6 = 15
52
= 65
5 x (25 + 1) / 2 = 65
110
1 + 7 + 13 + 19 + 25 = 65
3 + 8 + 13 + 18 + 23 = 65
5 + 9 + 13 + 17 + 21 = 65
11 + 12 + 13 + 14 + 15 = 65
72
= 175
7 x (49 + 1) / 2 = 175
1 + 9 + 17+ 25 + 33 + 41 + 49 = 175
4 + 11 + 18 + 25 + 32 + 39 + 46 = 175
7 + 13 + 19 + 25 + 31 + 37 + 43 = 175
22 + 23 + 24 + 25 + 26 + 27 + 28 = 175
92
= 369
9 x (81 + 1) / 2 = 369
1 + 11 + 21+ 31 + 41 + 51 + 61 + 71 + 81 = 369
5 + 14 + 23 + 32 + 41 + 50 + 59 + 68 + 77 = 369
9 + 17 + 25 + 33 + 41 + 49 + 57 + 65 + 73 = 369
111
37 + 38 + 39 + 40 + 41 + 42 + 43 + 44 + 45 = 369
3 x (9 + 1) / 2 = 15
5 x (25 + 1) / 2 = 65
7 x (49 + 1) / 2 = 175
9 x (81 + 1) / 2 = 369
11 x (121 + 1) / 2 = 671
13 x (169 + 1) / 2 = 1105
15 x (225 + 1) / 2 = 1695
17 x (289 + 1) / 2 = 2465
19 x (361 + 1) / 2 = 3439
99 x (9801 + 1) / 2 = 485.199…
112
8. Cuerpo Numérico
Un plano cartesiano (nombrado así en honor del matemático francés René Descartes,
quien formalizo su uso en las matemáticas) está definido por dos líneas de números
perpendiculares: el eje de las x, que es horizontal, y el eje de las y, que es vertical.
Usando estos ejes, podemos describir cualquier punto en el plano usando una pareja
ordenada de números.
El plano cartesiano se extiende infinitamente en todas direcciones. Para mostrar esto,
los libros de matemáticas usualmente colocan flechas en los extremos de los ejes en
sus dibujos.
Tomando como punto de partida el plano numérico tradicional con todos sus atributos,
que como sabemos es de posición horizontal, Sergio Aschero propone insertar un
segundo plano perpendicular al anterior en posición de atravesar centradamente el
primer plano.
113
Esto implica un cambio espacial en la definición del campo aritmético que se define en
principio con cuatro zonas: la del semiplano de los números racionales positivos
(derecha), la del semiplano de los números racionales negativos (izquierda), la del
semiplano de los infranúmeros (abajo) y la del semiplano de los ultranúmeros (arriba).
En el campo numérico de Aschero, existen tres tipos de cero, todos ellos ubicados en
el mismo punto de intersección de los dos planos: el lugar del cero tradicional.
Estos son: el cero tradicional en su posición conocida, el infra cero habilitante del
espacio inferior (entrante) y el ultra cero que completa esta trilogía permitiendo el uso
del espacio superior (saliente).
114
Con respecto a los infinitos, estos son cuatro: el infinito de los números reales
positivos, el infinito de los números reales negativos, el infra infinito de los
infranúmeros reales y el ultra infinito de los ultranúmeros reales. El campo imaginario
también se integra en el mismo modelo de cuatro variables.
Los infranúmeros con su capacidad de cuantificar las pérdidas y los ultranúmeros con
la suya de establecer un lugar preciso para los números imposibles de fijar mediante la
matemática tradicional, hacen de esta dualidad algo similar a la capacidad del dios
Jano con su posibilidad de ver simultáneamente el ayer y el mañana.
115
El número cero ocupa un papel primordial en la historia del desarrollo de la abstracción
por parte del ser humano. Aunque se dice que filosóficamente aparece en la cultura
de la India hace unos 17000 años, no es hasta hace alrededor de 1500 años que se
incorpora como cifra en los cálculos matemáticos.
Lo primero que hay que decir sobre el cero es que hay dos usos para el cero, ambos
extremadamente importantes, pero algo distintos. Un uso es como indicador de lugar
vacío en nuestro sistema numérico de valor por posición. Así pues en un número como
2106 el cero es usado para que las posiciones de 2 y de 1 sean correctas. Claramente
216 significa algo bastante distinto. El segundo uso del cero es como un número
mismo en la forma que lo usamos como 0. Hay también otros aspectos distintos del
cero en estos dos usos, a saber, el concepto, la notación y el nombre. (Nuestro
nombre "cero" deriva del árabe "sifr" el cual también nos da la palabra "cifra".)
Ninguno de los usos de arriba tiene una fácil descripción histórica. No sucedió que
alguien inventó las ideas y entonces todo el mundo comenzó a usarlas. También es
justo decir que el número cero está lejos de ser un concepto intuitivo. Los problemas
matemáticos comenzaron como problemas "reales" más que como problemas
abstractos. Los números en los primeros momentos de la historia eran concebidos de
una forma mucho más concreta que los abstractos conceptos que son nuestros
números de hoy.
Podemos ver de esto que el primer uso del cero para denotar un espacio vacío no es
en realidad un uso del cero como número después de todo, sino meramente el uso de
algún tipo de signo de puntuación para que los números tengan una interpretación
correcta.
Los antiguos griegos comenzaron sus contribuciones a las matemáticas sobre la
época en la que el cero como indicador de posición vacía empezaba a usarse por los
matemáticos babilonios. Los griegos sin embargo no adoptaron un sistema
numérico posicional. Merece la pena pensar lo significativo que es este hecho. ¿Cómo
116
podían con los brillantes avances matemáticos de los griegos no verlos adoptar un
sistema numérico con las ventajas del sistema de valor por posición que poseían los
babilonios? La verdadera respuesta a esta pregunta es más sutil que la simple
respuesta que vamos a dar, pero básicamente los logros matemáticos griegos estaban
basados en la geometría. Aunque la obra Elementos de Euclides contenía un libro
sobre Teoría Numérica, este estaba basado en la geometría. En otras palabras, los
matemáticos griegos no necesitaban nombrar los números dado que trabajaban con
números como longitudes de una línea. Los números que requerían ser nombrados
eran usados por los mercaderes, no por los matemáticos, y de aquí que no
necesitasen una notación clara.
Aunque existieron excepciones a lo que hemos afirmado. Las excepciones fueron los
matemáticos que estaban involucrados en el registro de datos astronómicos. Aquí
encontramos el primer uso del símbolo que hoy reconocemos para el cero, los
astrónomos griegos comenzaron a usar el símbolo O. Hay muchas teorías acerca de
por qué se usó este símbolo en particular. Algunos historiadores están a favor de la
explicación de que es omicrón, la primera letra de la palabra griega para nada, es decir
"ouden". Neugebauer, sin embargo, descarta esta explicación dado que los griegos ya
usaban omicrón como un número – representaba el 70 (el sistema numérico de los
griegos estaba basado en su alfabeto). Otra explicación ofrecida incluye el hecho de
que significa "obol", una moneda sin casi valor, y que surge cuando se usaban fichas
para contar en una tabla de arena. La sugerencia aquí es que cuando se eliminaba
una ficha para dejar una columna vacía el hueco en la arena parecía un O.
Ptolomeo en Almagest, escrito alrededor del 130 d.C, usó el sistema babilonio
sexagesimal junto con el parámetro de vacío O. En esta época Ptolomeo usaba el
símbolo tanto entre dígitos como al final del número y uno estaría tentado a creer que
al menos el cero como parámetro vacío se había establecido con firmeza.
Esto, sin embargo, está lejos de lo que sucedió. Solo unos pocos astrónomos
excepcionales usaron la notación y cayeron en desuso varias veces antes de
establecerse finalmente. La idea del lugar cero (ciertamente no concebido como un
número por Ptolomeo quien aún lo consideraba un signo de puntuación) hace su
siguiente aparición en los matemáticos indios.
La escena ahora se mueve a la India donde es justo decir que nacieron los números y
sistemas numéricos los cuales evolucionaron en los sistemas altamente sofisticados
que usamos hoy. Por supuesto, no hace falta decir que el sistema indio debía algo a
los sistemas previos y muchos de los historiadores de las matemáticas creen que el
uso indio del cero evolucionó del usado por los astrónomos griegos. Así como algunos
historiadores parecen querer quitar importancia a la contribución de los indios de una
forma poco razonable, hay también quienes afirman que los indios inventaron el cero,
lo que me parece ir demasiado lejos.
Lo cierto es que alrededor del año 650 d.C el uso del cero entró en la matemática
india. Los indios usaron también un sistema de valor por posición y el cero se usaba
para denotar un lugar vacío.
117
Alrededor del 500 d.C, Aryabhata ideó un sistema numérico que no tenía aún el cero y
que era un sistema posicional. Usó la palabra "kha" para la posición y sería usado más
tarde como nombre para el cero. Hay pruebas de que se había usado el punto en los
primeros manuscritos indios para denotar un espacio vacío en la notación posicional.
Es interesante que los mismos documentos a veces también usen un punto para
denotar algo desconocido donde nosotros usaríamos x.
El brillante trabajo de los matemáticos indios fue transmitido a los matemáticos árabes
e islámicos.
Es importante hacer notar en este punto que hubo otra civilización que desarrolló un
sistema numérico de valor por posición con el cero. Fueron los mayas, que vivieron en
Centro América. Esta fue una antigua civilización que floreció particularmente entre el
250 y 900. Sabemos que sobre el 665 usaron un sistema numérico de valor por
posición de base 20 con un símbolo para el cero. Sin embargo, su uso del cero iba
más allá de esto y estaba en uso antes de que lo introdujesen en el sistema numérico
de valor por posición. Esto es un notable éxito pero desgraciadamente no influenció a
otras culturas.
Fibonacci fue una de las principales personas en traer estas nuevas ideas sobre
sistemas numéricos a Europa. Se considera que fue un importante nexo entre el
sistema numérico Arábico-Hindú y el de los matemáticos europeos.
En Liber Abaci describe los nueve símbolos indios junto con el signo 0 para los
europeos alrededor del año 1200 pero no fue usado ampliamente hasta bastante
tiempo después. Es significativo que Fibonacci no fue lo bastante audaz como para
tratar el 0 de la misma forma que al resto de números 1, 2, 3, 4, 5, 6, 7, 8, 9 dado que
habla de la "marca cero" mientras que al resto de símbolos los llama números. Aunque
traer los números indios a Europa fue claramente de una gran importancia podemos
ver en su tratamiento del cero no alcanzó el mismo nivel de los indios
Brahmagupta, Mahavira y Bhaskara ni la de los matemáticos árabes e islámicos como
Al-Samawal.
El infranúmero es un nuevo concepto matemático que determina la diversidad de lo no
existente, actuando como una alternativa eficaz y lógica ante la invariabilidad del cero
tradicional que no tiene en cuenta el desarrollo de las diversas operaciones que
finalizan o pasan por él.
Desde el momento en que existe un dato distinto a la nada (singularidad irrepetible),
contamos con una energía numeral que llegará a ser infranumeral en el caso de lograr
su completa interferencia con las operaciones lógicas del sistema.
El infranúmero es la energía resultante de una operación de interferencia total, con la
interferencia parcial se está dentro de la zona numeral o ultranumeral.
El infranúmero determina una nueva noción matemática de fundamental importancia
con el fin de poder operar sobre cantidades de elementos que expresan medidas de
entidades no materiales.
Es energía cuantificada neutra surgida de todas las pérdidas operativas.
Se considera físicamente interferencia cuando dos ondas se superponen en oposición
de fase.
118
Si las ondas son de igual frecuencia y amplitud, la interferencia resulta total,
(infranúmero).
Desde el punto de vista acústico, si se colocan dos tubos de órgano iguales,
supongamos que de una frecuencia de 256 Hz. cada uno; acoplados a la misma caja
de aire y se sopla en ambos, no oiremos un sonido más fuerte, sino sólo el aire que
escapa.
También un haz de luz viene a estar compuesto por un tren de ondas. Cuando dos
haces luminosos de iguales características chocan entre sí, su energía se interfiere
provocándose la oscuridad; pero la energía no ha desaparecido.
Una de las reglas fundamentales de la física dice que la energía no puede
desaparecer.
Tal es la ley de conservación de la energía.
En el fenómeno de la interferencia hay una energía que ha dejado de existir en forma
de luz.
Por tanto, tiene que aparecer una cantidad exactamente igual de energía en otra forma
distinta; y en este caso es el calor.
Supongamos que damos cuerda al resorte de un reloj; ahora contiene más energía
que cuando estaba distendido.
A continuación disolvemos el resorte todavía tenso, en un ácido. ¿Qué ocurre con la
energía?
También aquí se convierte en calor.
Si empezamos con dos soluciones ácidas a la misma temperatura y disolvemos en
una de ellas el muelle distendido y en la otra un muelle tenso (por lo demás idénticos),
la segunda solución tendrá al final una temperatura mayor que la primera.
La propia materia es una forma de energía.
Cuando las matemáticas entiendan al número como energía (es decir cuando las
matemáticas y la física se unifiquen matecinéticamente), se descubrirá que el cero y el
infinito son dos conceptos inútiles en cualquier operación lógica por su propia
condición inabarcable.
Por otro lado, el lenguaje matemático incurre algunas veces en inexactitudes debido a
su limitada capacidad para representar ciertos resultados.
Esto se soluciona en parte al incorporar la serie infranumeral.
Todo movimiento que salga, pase o llegue por el punto infranumeral es algo que debe
ser medido con exactitud.
5 – 5 = 5 (cinco menos cinco es igual a infra cinco)
119
Los socráticos asociaban a la idea de infinito a algo malo, perverso. El infinito no solo
era lo descomunal, enormemente grande, lo indefinido, sino que estaba asociado a
idea negativa de desorden de caos, lo imperfecto.
En la Grecia clásica se utilizaba la expresión apeiron que significa sin fin, sin límite, lo
infinito, lo ilimitado o lo carente de definición, sin medida. Por tanto, se podía
interpretar que en el apeiron destacan connotaciones éticas como el caos.
Algunos autores veían en el concepto de infinito la idea aniquilación o absorción.
El concepto de infinito desde la perspectiva filosófica ha sido ampliamente discutido
pues induce a contradicciones y paradojas, desde Euclides, (el todo no es mayor que
las partes), la paradoja de Zenon (¿cómo recorrer una infinidad de mitades en un
tiempo finito?) o la Russell (el conjunto de conjuntos que no pertenecen a sí mismo). O
el Hotel de Hilbert.
El símbolo atribuido a infinito fue introducido por el matemático inglés John Wallis en
1655. Posee la forma de la Lemniscata de Bernoulli, aunque realmente se desconoce
de dónde Wallis sacó la idea. Muchos comentan que tiene la forma de una cinta de
Moebius, pero no es cierto, ya que el descubrimiento de August Moebius fue posterior.
La idea del infinito actual surge al considerarlo como una unidad. Esto es, tenemos
una (en el sentido de unidad) "cosa" que es infinitamente grande o numerosa, como
los números naturales o los números múltiplos de 27. Lo tratamos como si fuese un
elemento que surge al superar la idea del límite. Aparece cuando ya hemos llegado,
cuando tenemos el total.
Esta idea nos crea dificultades pues no tenemos un infinito, sino muchos, lo que
supone dificultades para la comparación y en definitiva para la medición. En efecto,
admitiendo la existencia del infinito actual, pues muchos matemáticos la negaron como por ejemplo Cauchy, Gauss-, es fácil demostrar que tenemos varios infinitos, lo
que implica que unos son diferentes de otros y, por tanto, de distintos tamaños. Esto
es, tendremos unos infinitos mayores que otros.
De manera intuitiva, si consideramos los números múltiplos de 27 y los números
naturales, ambos son infinitos, aunque "parece" que el primero es 27 veces más
pequeño que el segundo, sin embargo, ambos son infinitamente grandes.
En términos lógicos podríamos decir que el segundo está contenido en el primero y,
teniendo en cuenta el postulado de Euclides, que establece que el todo es mayor que
las partes, ambos infinitos deberían ser distintos, pero no lo son, pues tienen el mismo
tamaño. Llamamos tamaño de un conjunto a su cardinal, y el cardinal de ambos
conjuntos es el mismo, como demostró Cantor.
El razonamiento de Cantor es simple. Basta con comprobar que se puede establecer
una correspondencia biunívoca entre el conjunto de los números naturales y el
conjunto de los múltiplos de 27, de manera que estos conjuntos son equipolentes
(tienen el mismo número cardinal). De la misma forma se pueden numerar los puntos
de una semicircunferencia o los puntos de una recta.
120
Las ideas de Cantor de que había unos infinitos más infinitos que otros, además de
llevar al escándalo, condujo a la formalización y ampliación de ciertos conceptos como
el de cardinalidad y ordinalidad.
Así como el infranúmero cuestiona la existencia del cero como único símbolo
representativo de la nada, el ultranúmero actúa como símbolo inverso de aproximación
al concepto del todo, identificado tradicionalmente por el infinito y en el modelo de
Aschero con el ultra cero. Un mismo punto bidireccional de polo positivo y negativo,
origina y finaliza lo incontable, que se extiende más allá y más acá de toda serie
numérica, tanto como se desee. Si el número avanza, el ultranúmero retrocede y en la
medida que se aleja su magnitud decrece, con lo cual se invierten todas las
operaciones aritméticas. Con el número y el infranúmero se cuenta, con el ultranúmero
se descuenta. El absoluto es mensurable mediante el ultra cero, y así se define uno de
los límites que ayuden de una vez por todas a solucionar alguno de los enigmas y
contradicciones más importantes del lenguaje matemático. Para esto se establece la
serie ultranumeral.
Es tan lógico contar a partir de la nada como descontar a partir del todo.
Cada ultranúmero que proceda del todo es algo que debe ser medido con exactitud,
para así establecer su magnitud, que tiene una progresión decreciente en la medida
que se aleja de su punto de partida: el ultra cero.
La serie ultranumeral es ilimitada y se utiliza indistintamente para los ultranúmeros
reales y los imaginarios.
1 : 0 = 1 (uno dividido cero es igual a ultra uno)
De esta forma la Ecuación de Wallis se resuelve: ultra uno es el uno más grande que
existe ya que es el número uno más próximo al ultra cero. En cambio, lo que es
imposible de determinar es el ultranúmero menor (el de mayor cantidad de cifras).
La frontera (o el puente) que vincula a los números con los ultranúmeros para permitir
el traspaso entre ambos es (por ahora) el gúgolduplex.
121
El gúgolduplex es uno de los números más grandes a los que se puso nombre. Así
como una hoja de papel lo suficientemente grande como para escribir todos los ceros
de un gúgolplex es más grande que el universo conocido, entonces, una hoja de papel
lo suficientemente grande como para escribir un gúgolduplex sería más grande que un
gúgolplex de universos como el nuestro.
Para la recta numérica el gugoldúplex es un meganúmero finito, y al pasar dicha
frontera se convierte en un ultranúmero muy pequeño, por la ley de la inversión que el
mundo ultranumeral establece, determinando que los ultranúmeros más grandes,
poseen las cifras más pequeñas:
Veamos ahora la serie de los primeros veintiséis ultranúmeros primos, empezando por
el mayor (ultra uno) y finalizándola con el menor de ellos (ultra noventa y siete).
1 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
Si no se considera al número uno como primo y sí al número dos, evidentemente el
número primo más grande es ultra dos.
122
123
9. Tactomatemática
Ceguera
El órgano receptor es el ojo cuando algunas de las partes constitutivas de la visión no
funciona adecuadamente e interfiere en la transmisión y percepción de las impresiones
luminosas en su viaje al cerebro se produce disminución visual o pérdida súbita.
Ceguera es la ausencia de percepción de la luz.
La vista, desde el momento del nacimiento, es un canal sensorial social. Según
estudios realizados, hasta los doce años la mayoría de las nociones aprendidas se
captan a través de las vías visuales, en una proporción del 83%, frente a los estímulos
captados por los otros sentidos, que se reparten entre el 17% de los restantes.
Los ojos que comienzan captando tan sólo un juego de luces y sombras, activan zonas
del cerebro que emiten respuestas motrices, y esta actividad sensorio-motriz es la
clave del desarrollo del niño/a. Lo que el ojo ve, quiere tocarlo con la mano y cuando
ha tocado aquello, quiere ir más lejos. A la primera etapa de concentración visual
sigue otra de atención, y a estas dos una tercera de reconocimiento visual.
Los sentidos funcionan en cinestesia, esto es, en dos o más modalidades ligadas. Ni
aún el primer sentido en desarrollarse, el tacto, funciona de forma pura.
Para definir las dificultades visuales, hay que tener en cuenta los siguientes aspectos:
• Agudeza visual: Es la capacidad que tiene el ojo para discriminar detalles como color,
forma, peso de un objeto a cierta distancia.
• Campo Visual: Es la amplitud de campo que un sujeto puede llegar a ver. Cuanto
más cerca del objeto menos campo visual.
• Debilidad de visión: Ambliopía, se conoce como ojo vago, lo provoca la ausencia de
uso de ese ojo o por la miopía, es irreversible y se detecta de los 3-4 años.
• Baja visión: Cuando un sujeto necesita de determinadas ayudas ópticas para poder
funcionar lo más adecuadamente como vidente.
En definitiva, la ceguera supone una discapacidad total para orientarse la imposibilidad
de leer aún con corrección óptica o magnificación de los textos escritos en tinta.
124
Tacto



El tacto, es uno de los sentidos de los seres humanos y de otros animales. A través
del tacto, el cuerpo percibe el contacto con las distintas sustancias, objetos, etc. Los
seres humanos presentan terminaciones nerviosas especializadas en la piel, que se
llaman receptores del tacto. Estos receptores se encuentran en la epidermis (capa
más externa de la piel) y transportan las sensaciones hacia el cerebro a través de las
fibras nerviosas. Hay sectores de la piel que poseen mayor sensibilidad ya que el
número de receptores varía en toda la piel.
Los receptores del tacto están constituidos por los discos de Merkel, que se subdividen
en las siguientes categorías:
Corpúsculos de Pacini: se ubican en la zona profunda de la piel, sobre todo en los
dedos de las manos y de los pies. En general son poco abundantes. Detectan
presiones y deformaciones de la piel, y sus estímulos duran poco.
Terminaciones nerviosas libres: están en casi todo el cuerpo y se especializan en
sentir el dolor.
Terminaciones nerviosas de los pelos: sensibles al tacto. La mayoría de los pelos son
de este tipo.
125



Corpúsculo de Meissner: se encuentran en las papilas dérmicas, abundantes en los
extremos de los dedos, los labios, la lengua, etc. Se ubican en la zona superficial de la
piel y se especializan por el tacto fino.
Corpúsculos de Krause: presentes en la superficie de la dermis y son sensibles al frío,
se ubican en especial en la lengua y en los órganos sexuales.
Corpúsculo de Rufino: son poco numerosos, alargados y profundos, son sensibles al
calor.
La piel:
Es una parte muy importante del organismo que protege y cubre la superficie del
cuerpo. Contiene órganos especiales que suelen agruparse para detectar las distintas
sensaciones como la temperatura y dolor.
El uso activo del tacto para "buscar y adquirir información" ha sido denominado "tacto
háptico". El "sistema háptico" ha sido definido como un sistema perceptual distintivo
orientado a la discriminación y al reconocimiento de objetos manipulándolos en lugar
de mirarlos.
Braille
El Braille, es el sistema utilizado por las personas ciegas, para poder leer. Este, un
sistema de escritura, funciona por medio de caracteres en relieve para permitir leer
usando los dedos de la mano.
Cada uno de estos caracteres o células, contiene seis posiciones de puntos,
posicionados en rectángulos, los cuales se encuentran en dos columnas de tres
puntos cada una. Cada uno de estos puntos, pueden ser levantados (darles relieve),
para que con los dedos, la persona no vidente pueda sentir esta protuberancia.
Cuando no hay ningún relieve, significa que existe un espacio.
La primera columna contiene los números del 1 al 3. Y la segunda, la que está
posicionada a la derecha, contiene los números del 4 al 6. Para ir desarrollando las
letras y los números, se realizan distintas combinaciones de relieve, con los diferentes
puntos existentes.
126
Las 10 (diez) cifras arábigas (del 0 al 9) se representan por medio de los 10 primeros
signos del alfabeto anteponiéndole el signo de número, que se forma con los puntos
(3-4-5-6)
Signo en Tinta
Descripción
1
(1)
2
(1-2)
3
(1-4)
4
(1-4-5)
5
(1-5)
6
(1-2-4)
127
7
(1-2-4-5)
8
(1-2-5)
9
(2-4)
0
(2-4-5)
Ej.: 1
Ej.: 12
Ej.: 153
Cuando un número tiene más de tres cifras, éstas se separan con un punto,
comenzando por las unidades. Para ello se utiliza el punto (3)
Ej.: 1.079
128
Signo en Tinta
Descripción
Significado
+
(2-3-5)
Suma
-
(3-6)
Resta
x
(2-3-6)
Multiplicación
/
(2-5-6)
División
=
(2-3-5-6)
Igual
Ej.: 1+2=3
La crítica que se le puede hacer al alfabeto Braille con respecto a la representación
simbólica de los números es que tiene poco que ver con la realidad objetual de lo
contable.
La Tactomatemática, en cambio tiene una identidad que la vincula absolutamente con
lo numerable, desde lo táctil y también desde lo visual.
Veamos:
129
130
131
132
133
134
135
136
137
138
139
INDICE
1. Una mirada desprejuiciada sobre el sistema de numeración (2)
2. La genetización numérica (14)
3. La identiplicación numérica (19)
4. Modelo decimal (41)
5. El nonúmero (91)
6. Números armónicos inmanentes (97)
7. Polisuma entrecruzada (109)
8. Cuerpo Numérico (112)
9. Tactomatemática (123)
© Sergio Aschero (Doctor en Musicología) sergioaschero@gmail.com
Avenida Roca 1669 (1870) Avellaneda / Provincia de Buenos Aires / Argentina
http://www.sergioaschero.com.ar
140