MIRA, MIRA ¿QUÉ VES

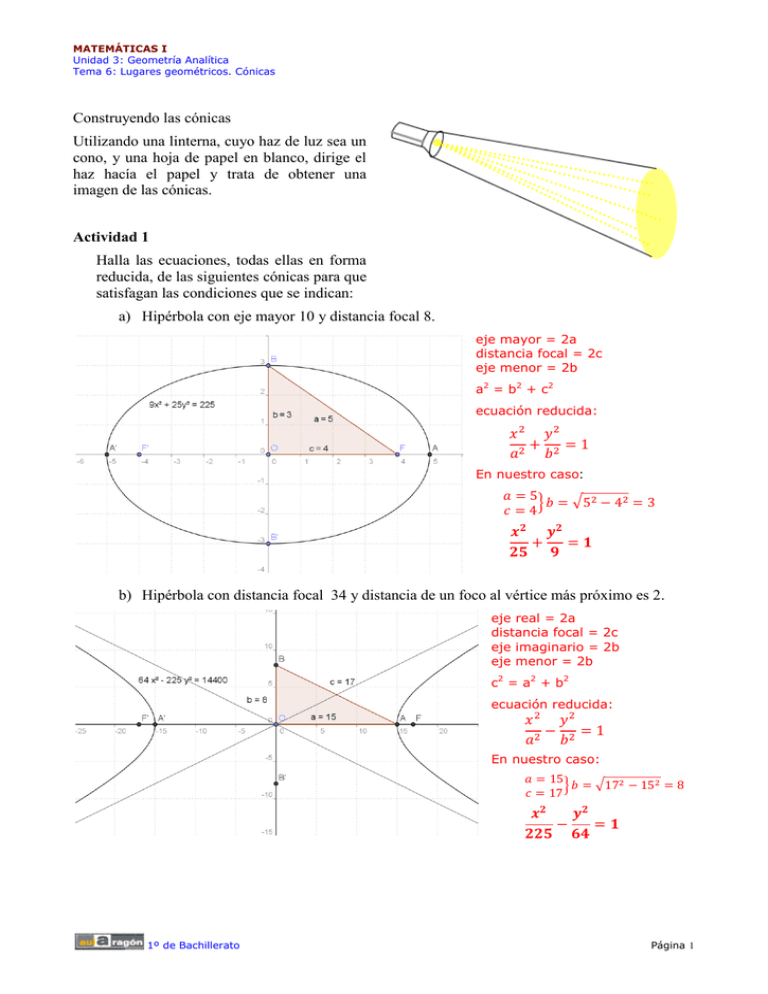
MATEMÁTICAS I
Unidad 3: Geometría Analítica
Tema 6: Lugares geométricos. Cónicas
Construyendo las cónicas
Utilizando una linterna, cuyo haz de luz sea un
cono, y una hoja de papel en blanco, dirige el
haz hacía el papel y trata de obtener una
imagen de las cónicas.
Actividad 1
Halla las ecuaciones, todas ellas en forma
reducida, de las siguientes cónicas para que
satisfagan las condiciones que se indican:
a) Hipérbola con eje mayor 10 y distancia focal 8.
eje mayor = 2a
distancia focal = 2c
eje menor = 2b
a2 = b2 + c2
ecuación reducida:
En nuestro caso:
b) Hipérbola con distancia focal 34 y distancia de un foco al vértice más próximo es 2.
eje real = 2a
distancia focal = 2c
eje imaginario = 2b
eje menor = 2b
c2 = a2 + b2
ecuación reducida:
En nuestro caso:
1º de Bachillerato
Página 1
MATEMÁTICAS I
Unidad 3: Geometría Analítica
Tema 6: Lugares geométricos. Cónicas
c) Parábola con directriz y = 4 y vértice (0, 0).
Como
Descubriendo cónicas
Puede que al pasear por los jardines de tú ciudad te hayas
percatado de que entre los parterres hay bastantes con forma
de elipse, es fácil de suponer que los jardineros no tienen una
formación matemática ni de dibujo técnico que le permitan
hacer tales dibujos. ¿Qué método habrán empleado? Trata de
reproducir en tú cuaderno el método utilizado
Elipse de jardinero
Creative Commons
Actividad 2
Halla las ecuaciones de las siguientes elipses de forma que satisfagan las condiciones que se
indican:
a) Focos(±4,0), vértices(±5,0)
b) Focos(0,±7), semieje menor = 4
c) Focos(±3,0), excentricidad 0,6
1º de Bachillerato
Página 2
MATEMÁTICAS I
Unidad 3: Geometría Analítica
Tema 6: Lugares geométricos. Cónicas
Usando las ecuaciones de las cónicas
Actividad 3
Sistema solar
Dominio público
Vamos a hora a aprovechar la primera ley de Kepler, por
ella sabemos que la trayectoria que describe la tierra es
una elipse de excentricidad 0,0161 y de 148,5 millones
de kilómetros de semieje mayor. En uno de los focos
está el sol. Calcula la ecuación de la elipse y la máxima
y mínima distancia de la Tierra al Sol.
Ecuación reducida de la elipse:
Distancias de Tierra al Sol:
Mínima: a-c = 148,5 – 2,39 = 146,11 millones de kilómetros
Máxima: a+c = 148,5 + 2,39 = 150,89 millones de kilómetros
CRITERIOS DE EVALUACIÓN
A las tres cuestiones se les da el mismo valor.
En la primera de las cuestiones se trata de que el alumno repita el proceso de obtención de
las cónicas, en este caso el haz de luz es el cono y la hoja de papel el corte. El alumno debe explicar
la posición que ha de tener el papel con respecto al haz e identificar la figura obtenida. Debe
aplicarlo a la resolución de los ejercicios
En la segunda cuestión se trata de un pequeño trabajo de investigación y descubrir la forma
práctica de dibujo de elipses y aprender a obtener sus ecuaciones.
En el tercero el alumno debe conocer la elipse, su ecuación y elementos característicos y
utilizando estos calcular los elementos de la elipse que describe el Sol en su “movimiento alrededor
de la tierra”
1º de Bachillerato
Página 3