Instituto Libre de Segunda Enseñanza / ( ) 1 f x to Libre de Segunda
Anuncio
Instituto Libre de Segunda Enseñanza
Guía de repaso: EVALUACIÓN INTEGRADORA
4to año
1
1. Sea f : ℝ → ℝ / f ( x ) = 3.3x − , se pide:
9
a) Redefinir f de modo tal que sea biyectiva y definir f *−1 .
b) Graficar f . (Dar ecuaciones de las asíntotas e indicar intersecciones con los ejes).
19
c) Resolver la siguiente ecuación: f ( x) − 3− x = − .
9
1
d) Redefinir f, de modo tal que Im( f ) = − , 0
9
x+a
2. Sea f −1 : ( −4, +∞ )
→ ℝ / f −1 ( x ) = log 1
2) un punto de f , se pide:
+ b biyectiva y (1;-2)
2
2
a) Determinar a y b.
b) Definir f.
c) Graficar ambas funciones en un mismo sistema de ejes coordenados.
d) Determinar las coordenadas de los puntos de intersección de los gráficos de f −1 y
t ( x ) = log 2 ( x + 4 ) , siendo f −1 la función hallada en a).
2
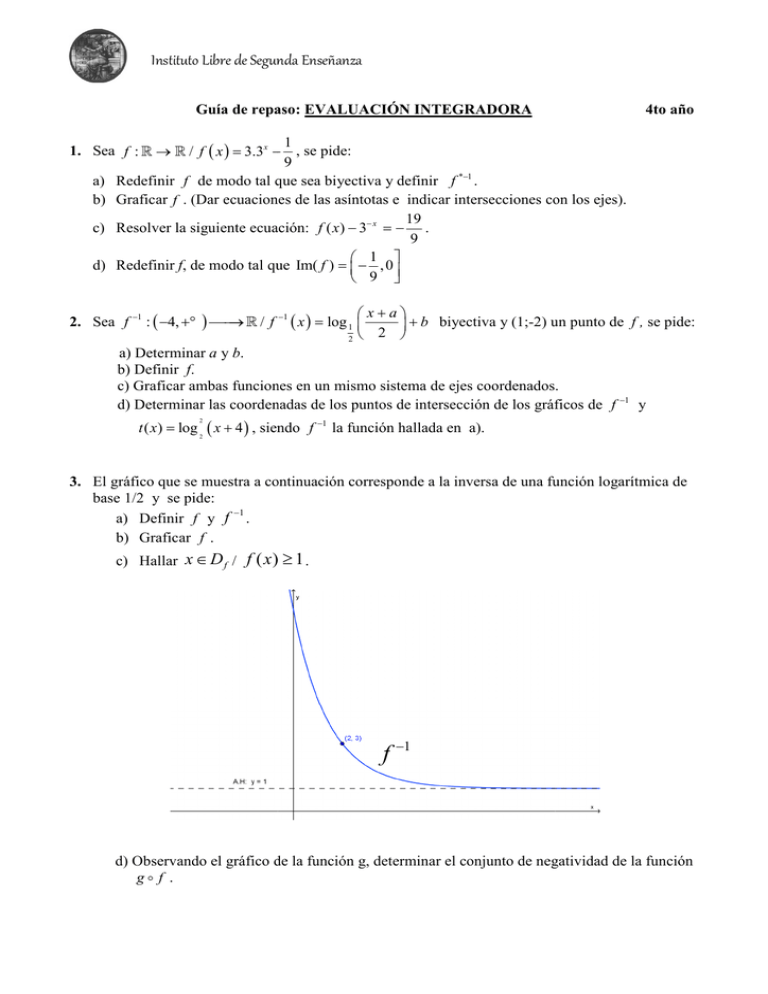
3. El gráfico que se muestra a continuación corresponde a la inversa de una función logarítmica de
base 1/2 y se pide:
−1
a) Definir f y f .
b) Graficar f .
c) Hallar x ∈ D f / f ( x ) ≥ 1 .
f −1
d) Observando el gráfico de la función g, determinar el conjunto de negatividad de la función
g f .
Instituto Libre de Segunda Enseñanza
4. Sea f : ℝ → B / f ( x ) = 3x −1 + 1 , se pide:
a) Hallar B, de manara que f sea biyectiva. Definir f −1 .
b) Graficar f y f −1 . (Dar ecuaciones de las asíntotas e indicar intersecciones con los ejes).
c) Resolver la siguiente ecuación: log 2 ( 9 x −1 + 7 ) = 2 + log 2 ( f ( x ) ) .
d) Hallar x ∈ ℝ / f ( x) − 28 ≥ 0 .
5. Se muestran los gráficos de una función logarítmica de base 4, una función exponencial y sus
respectivas asíntotas con línea punteada. Dar la fórmula de cada función.
Instituto Libre de Segunda Enseñanza
π
π π
6. Dada las funciones h : − ,
→ R / f ( x) = 2 x − 2 , se
→ ℝ / h( x ) = sen 4 x − y f : R
2
2 2
pide:
a) Determinar las coordenadas de los máximos de h.
b) Graficar h y f h . (Indicar ceros, máximos y mínimos)
π
7. Dada la función h : ℝ
→ ℝ / h( x) = 2sen x + y se pide:
2
a) Graficar h.
b) Definir una función equivalente a h(x
h(x) con ángulo de desfasaje nulo.
c) Dar la expresión de la función lineal T de manera tal que: Im (T h ) = [1, 7] .
d) Utilizando la expresión de h(x) hallada en b), resolver las siguientes ecuaciones en los
dominios indicados:
5
1
d1) − sen 2 x = h( x ) x ∈ ℝ .
4
2
d2) h ( 3x ) = 3tg ( 3x ) ; x ∈ [ 0, π ] .
2
1
d3) 3tg ( x ) = 4
+ 1 ; x ∈ [0,2π ] .
h( x )
2
8. Hallar todos los valores de x ∈ [ − π ,3π ] tales que: 4 ( log 2 ( cos x ) ) + log 2 (1 + cos 2 x − sen 2 x ) = 3
2
9. Dado el siguiente gráfico, se pide:
f
a) Determinar las coordenadas de los puntos: A, B, C, D y E.
f
Instituto Libre de Segunda Enseñanza
b)
Dar la expresión de una función lineal T, de modo que el gráfico de f T sea simétrico
respecto del eje y.
c) Sobre el mismo sistema de ejes del ejercicio anterior, graficar la función:
π π
g : − ;
→ ℝ / g ( x ) = 2 sen ( 4 x )
4 2
10. Observando los siguientes gráficos, se pide:
a) Hallar las fórmulas de las funciones trigonométricas f y g (en ambos casos utilizar ángulo de
fase nulo)
b) Dar las coordenadas del punto A.
11. Dada la función f : D
→ ℝ / f ( x ) = log 2 ( x − 1) − log 4 ( x − 1) − 3 , se pide:
a) Graficar f considerando D: dominio más amplio.
amplio (Sugerencia: considere la expresión
simplificada de f)
b) Modificar el dominio considerado en a) de modo que Im f = Im g , siendo
2
−x
3
1
9
g : − ; +∞ → ℝ / g ( x ) = − +
2
2
4
Instituto Libre de Segunda Enseñanza
12. Los puntos A y B tienen ordenada 3 y 1 respectivamente y pertenecen al gráfico de la función
trigonométrica que se muestra.
a) Determinar una fórmula para el gráfico de la función trigonométrica dada.
b)Determinar las coordenadas de los puntos A y B.
RESPUESTAS
1
1
1) a) f *−1 : − , +∞
→ ℝ / f *−1 = l og 3 x + − 1
9
9
b)
c) S = {−1}
Instituto Libre de Segunda Enseñanza
d) f : ( −∞, −3] → ℝ / f ( x ) = 3.3x −
2) a) a =4, b =1
1
9
15
→ ( −4, +∞ ) / f ( x) = 22− x − 4 d) ( −2,1) y − , 4
b) f : ℝ
4
c)
y=x
f −1
f
3) a) f : ( 1,+∞ )
→ ℝ / f ( x ) = log 1 ( x − 1) + 3
f
2
−1
: ℝ
→ (1, +∞ ) / f
−1
1
( x ) =
2
x −3
b)
f
c)
(1,5]
d) Cg− f = ( 3;9 )
→ ℝ / f −1 ( x) = log 3 ( x − 1) + 1 c) S = {1; 2} d) x ∈ [ 4; +∞ )
4) a) B = (1, +∞ ) f −1 : (1, +∞ )
x
5)
1
y = 6 − 2
9
1 5
y = l og 4 x − −
2 6
+1
Instituto Libre de Segunda Enseñanza
6)
π
π π
f h : − ,
→ ℝ / ( f h ) ( x) = 2.sen 4 x − − 2
2
2 2
π π
π
3π
π
3π
Máximos de h: − ;1 ;1 ceros de h.: − ;0 − ;0 ;0 ;0
4 4
8 8 8 8
7)
a)
Instituto Libre de Segunda Enseñanza
b)
3
x+4
2
π 5π 13π 17π
π 3π 5π 7π
m,k ∈ ℤ d2) S = ; ;
;
d3 ) S = ; ; ;
18 18 18 18
4 4 4 4
h : ℝ
→ ℝ / h( x) = 2 cos ( x )
5π
π
d) d1) S = + 2k π; + 2mπ
3
3
c) T( x ) =
π π 5π 7π
8) S = − ; ; ;
3 3 3 3
π
π
π
f : − , π → ℝ / f (x ) = 2sen(3
2 sen(3x − π ) + 1
2
9) a) Algunas posibles definiciones de f :
f : − , π → ℝ / f (x ) = −2sen (3x ) + 1
2
3
f : − , π → ℝ / f (x ) = 2cos(3x − π ) + 1
2
2
1
5
π
7
11
π ;2 B = − π ;2 C = π ;2 D = π ;2 E = ; −1
6
18
18
18
18
A = −
b) Existen infinitas posibilidades, tres posibles: T( x ) = x +
π
6
T( x ) = x −
π
6
c)
10) a)
11) a)
f (x ) = 4 sen(5x )
g (x ) = −4 cos(5x )
31
π ; −2 2
20
b) A =
T( x ) = x −
π
2
Instituto Libre de Segunda Enseñanza
b) D = [5;9 )
3
12) f : ℝ
→ ℝ / f ( x ) = 4 sen 3 x − π − 1
2
10
37
π ;3 B =
π ;1
3
9
A=
f : ℝ
→ ℝ / f ( x) = 4 cos ( 3x ) − 1




![( ) ( ) f z Log z = [ ( )]j sen h π ( ) f z sen z = ( , ) 2 4, 6 2 A x y x y](http://s2.studylib.es/store/data/004505423_1-0a27ac3b094722841476bfccc948b35f-300x300.png)