RELACION CARGA2
Anuncio
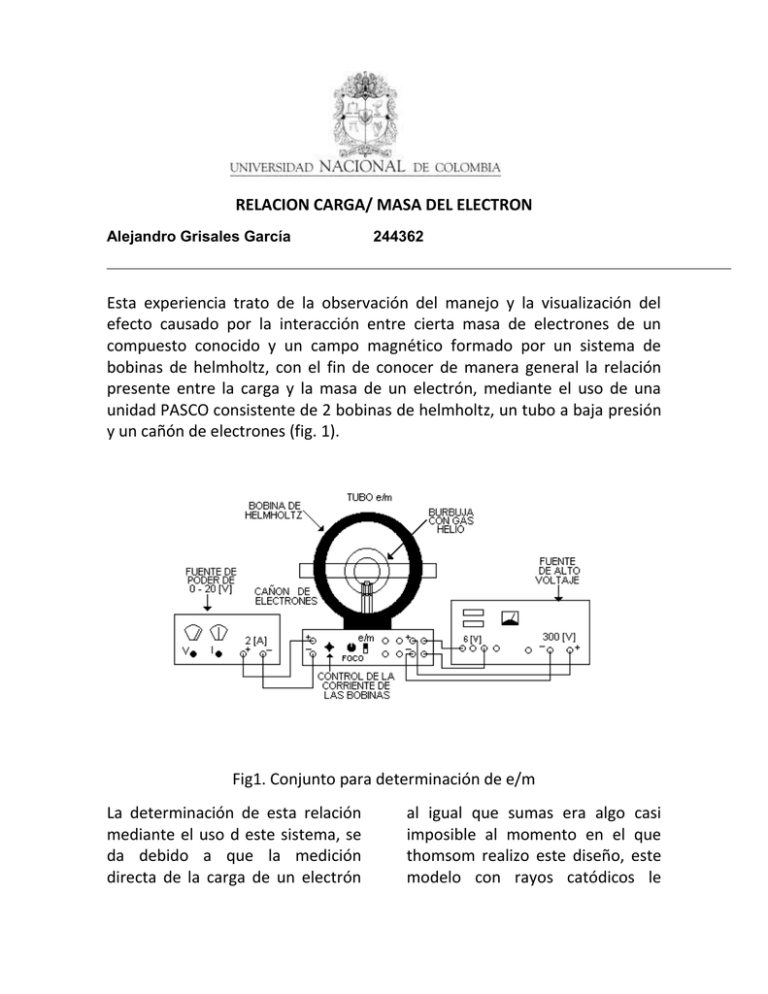
RELACION CARGA/ MASA DEL ELECTRON Alejandro Grisales García 244362 Esta experiencia trato de la observación del manejo y la visualización del efecto causado por la interacción entre cierta masa de electrones de un compuesto conocido y un campo magnético formado por un sistema de bobinas de helmholtz, con el fin de conocer de manera general la relación presente entre la carga y la masa de un electrón, mediante el uso de una unidad PASCO consistente de 2 bobinas de helmholtz, un tubo a baja presión y un cañón de electrones (fig. 1). Fig1. Conjunto para determinación de e/m La determinación de esta relación mediante el uso d este sistema, se da debido a que la medición directa de la carga de un electrón al igual que sumas era algo casi imposible al momento en el que thomsom realizo este diseño, este modelo con rayos catódicos le permitió asegurar la presencia de partículas con masa y carga presentes en el gas contra el que chocan los rayos catódicos, esto debido a la presencia de la inercia, que se observa debido a la desviación de los rayos. Como sabemos mediante la ley de lorentz podemos determinar la fuerza magnética que actúa sobre una partícula con carga q y velocidad u y campo magnético B como se ve a continuación: Fm=qu x B Ec.1 fuerza de lorentz En el experimento propuesto por thomson, la dirección del campo magnético producido por el diseño de las bobinas de helmholtz, es perpendicular al vector velocidad u, es así como la ecuación puede reescribirse de la siguiente manera: Fm=euB Ec.2 fuerza magnética producida por u campo magnético perpendicular a la velocidad Donde e es la carga del electrón, debido a que la trayectoria descrita por el conjunto es circular, los electrones se moverán a lo largo de esta trayectoria, produciéndose un fuerza centrípeta descrita por la ecuación: Fc=m (u^2/r) Ec.3 fuerza centrípeta para una partícula Con m la masa del electrón, u su velocidad, y r el radio del circulo q este describe, debido a que la única fuerza existente es la causada por el campo magnético es posible suponer que Fm=Fc, igualdad que podemos combinar con el fin de obtener la siguiente expresión para la relación de la carga del electrón sobre su masa: 𝑒 𝑢 = 𝑚 𝐵𝑟 Ec. 4 relación carga del electrón/ masa el electrón en términos de su velocidad, el campo magnético y el radio que describe. Como se sabe calcular la velocidad de las partículas y el campo magnético producido puede ser tedioso es por eso que esta expresión puede expresarse de modo que quede en función de términos que puedan ser medidos con mayor facilidad como el voltaje administrado al sistema, la permeabilidad del mismo, el numero de vueltas de alambre en cada bobina, entre otros, lo cual es posible mediante las siguientes determinaciones: a. la energía cinética que ganan los electrones debido al voltaje administrado viene dada por la expresión: 1 𝑒𝑣 = 𝑚𝑢2 2 Ec. 5 energía cintica ganada por los electrones del sistema b. el campo magnético producido por las bobinas de helmholtz es aproximadamente uniforme en su región central y puede expresarse de la siguiente forma: 𝐵= 8𝜇0 𝑛𝐼 5√5𝑎 Ec. 6 campo magnético generado por las bobinas de helmholtz en su región central Con a como el radio existente en las bobinas, 𝜇0 la permeabilidad magnética del vacío y n el numero de vueltas que tiene la bobina. Con las ecuaciones 4,5 y 6, podemos obtener una expresión que permita calcular el valor de e/m en función de voltajes y otros valores que sean más fáciles de obtener directamente, esa expresión es: 𝑒 125 𝑎 2 = ( ) 𝑉 𝑚 32 𝜇0 𝑛𝐼𝑟 Ec. 7 relación e/m en función de condiciones de entrada (I, V) y salida (a) En el caso de la practica realizada en el laboratorio, observamos como la interacción del rayo catódico con helio gaseoso, produjo un color azul, y una trayectoria circular bien definida para el caso en el cual el campo magnético golpeaba el tubo a baja presión, y que si el ángulo de incidencia variaba la trayectoria se convertía en un espira la cual según el sentido de la variación se extendía hacia el fondo o hacia el frente, esto debido a la influencia del ángulo en la ecuación de lorentz donde el valor del sin Θ ya no será uno y la fuerza tendrá una nueva componente. Con el color azul producido también podemos observar un nuevo dato arrojado por el experimento visto, según la escala proporcionada por el espectro electromagnético (fig. 2) de las partículas de helio, inferencia que le permitió a thomson formular modelos atómicos basado en su “creación”, el electrón, todo esto debido simplemente a la interacción que ocurre entre el haz de partículas con la masa de gas presente en el conjunto. Fig. 2 espectro electromagnético Como el color obtenido fue azul podemos ver que se encuentra en la gama de colores de alto grado de energía acercándose al valor del violeta. En conclusión del experimento observado, podemos sin necesidad de realizar cálculos inferir la existencia de la carga y de la masa BIBLIOGRAFIA 1. GUIA DE PRACTICA # 14, relación carga/masa del electro 2. http://portales.educared.net/wikiEducared/index.php?title=Modelo_at ómico_de_Thomson 3. http://www.deciencias.net/simulaciones/quimica/atomo/cargamasa.htm 4. http://www.ucm.es/info/Geofis/practicas/prac25r.pdf








![acelerador_fisica[1]](http://s2.studylib.es/store/data/000787223_1-9b400699727d499133235ec82e32a450-300x300.png)


