acelerador_fisica[1]

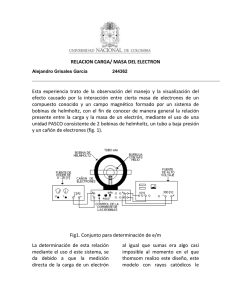
RELACIÓN CARGA MASA DEL ELECTRÓN
Daniela Angulo Páez
Luis Carlos Calderón Matallana
Diana Lucia Gómez Molina
Luis Alberto Figueroa Casallas
14 de mayo de 2010
RESUMEN
Para realizar el experimento usaremos un tubo de rayos catódicos, que consta de un cañón de electrones y
una ampolla transparente que contiene Helio como gas de relleno, que junto con un par de bobinas de
Helmholtz nos permitirá estudiar la trayectoria de un haz de electrones en un campo magnético orientado
perpendicularmente. El cañón de electrones está formado por un filamento que calienta un material que
actúa de cátodo emitiendo electrones por “efecto termoiónico”, y una placa metálica, a la que se aplica un
potencial positivo, que es el ánodo. Entre ambos electrodos, y cerca del cátodo, se coloca un segundo
electrodo (rejilla) que sirve para controlar el paso de electrones hacia el ánodo. El ánodo tiene un pequeño
orificio que permite al haz de electrones entrar en la ampolla de cristal. El choque de los electrones con los
átomos del gas He produce su ionización y, tras su recombinación con otros electrones, da lugar a una
emisión verdosa que permite apreciar la trayectoria seguida por los electrones. En el interior del tubo una
escala graduada constituida por cuatro barritas metálicas con pintura fluorescente que permitirá medir el
diámetro de la órbita de los electrones. Todo el conjunto se coloca en el centro de dos bobinas de Helmholtz
que proporcionan un campo magnético uniforme en la región en la que se realizarán las medidas. Una
fuente proporciona la alimentación de las bobinas, y la intensidad de la corriente puede controlarse con el
amperímetro (polímetro). Por otro lado los voltajes del tubo provienen de una fuente estabilizada que
proporciona un voltaje de calentamiento fijo de 6.3 V, mientras que el voltaje de rejilla y el anódico (tensión
de aceleración) pueden ajustarse entre –50 a 0 V, y entre 0 a +250 V.
INTRODUCCIÓN
J. J. Thomson físico
destacado al cual se
le
atribuye
la
primera descripción
de la relación de la
masa con la del
electrón, paso su
vida investigando
sobre
el
comportamiento
de
Figura 1. J.J. Thomson
partículas cargadas
eléctricamente cuando son expuestas a campos
eléctricos y magnéticos
Trabajos sobre los rayos catódicos
Thomson realizó una serie de experimentos en
tubos de rayos catódicos, que le condujeron al
descubrimiento de los electrones. Thomson
utilizó el tubo de rayos catódicos en tres
diferentes experimentos.
En su primer experimento, investigó si las cargas
negativas podrían ser separadas de los rayos
catódicos por medio de magnetismo. Construyó
un tubo de rayos catódicos que termina en un par
de cilindros con ranuras, esas hendiduras fueron
a su vez conectadas a un electrómetro. Thomson
descubrió que si los rayos son desviados
magnéticamente de tal manera que no puedan
entrar en las ranuras, el electrómetro registra
poca carga. Thomson llegó a la conclusión de que
la carga negativa es inseparable de los rayos.
En su segundo experimento investigó si los rayos
pueden ser desviados por un campo eléctrico.
Anteriores
experimentadores
no
habían
observado esto, pero Thomson creía que sus
experimentos eran defectuosos porque contenían
trazas de gas. Thomson construyó un tubo de
rayos catódicos con un vacío casi perfecto, y con
uno de los extremos recubierto con pintura
fosforescente. Thomson descubrió que los rayos
de hecho se podían doblar bajo la influencia de
un campo eléctrico.
En su tercer experimento (1897), Thomson
determinó la relación entre la carga y la masa de
los rayos catódicos, al medir cuánto se desvían
por un campo magnético y la cantidad de energía
que llevan. Encontró que la relación carga/masa
era más de un millar de veces superior a la del ión
Hidrógeno, lo que sugiere que las partículas son
muy livianas o muy cargadas.
Las conclusiones de Thomson fueron audaces: los
rayos catódicos estaban hechos de partículas que
llamó "corpúsculos", y estos corpúsculos
procedían de dentro de los átomos de los
electrodos, lo que significa que los átomos son,
de hecho, divisibles. Thomson imaginó que el
átomo se compone de estos corpúsculos en un
mar lleno de carga positiva; a este modelo del
átomo, atribuido a Thomson, se le llamó el
modelo de budín de pasas.
relación carga masa:
deduce:
𝐞
𝐦𝐞
=
𝐯
𝐦𝐞 𝐯𝟐
𝐑
= 𝐞𝐯𝐁 de donde se
𝐁∙𝐑
Esta última expresión permite hallar el cociente
carga/masa del electrón (y en general el de
cualquier partícula cargada) midiendo el radio de
la trayectoria descrita por éste cuando entra en
⃗
un campo magnético B
con velocidad
⃗ perpendicular al mismo. La primera medida de
v
esta magnitud la realizó J.J. Thomson en 1897.
Partes
El aparato consta de:
Figura 3. Partes del aparato e/m
Figura 2. Tubo de rayos catódicos de Thomson
Relación carga masa
Un electrón de carga e, que se mueve con
velocidad v
⃗ dentro de un campo magnético ⃗B, se
⃗ (fuerza de
encuentra sometido a una fuerza F
Lorentz), que es perpendicular en cada instante al
plano que contiene al campo y a la velocidad:
⃗ = 𝐞𝐯𝐁𝐬𝐞𝐧𝛗
𝐅 = 𝐞𝐯⃗ × 𝐁
donde ϕ es el ángulo formado por los vectores v
⃗
⃗.
yB
Esta fuerza imprime al electrón un movimiento
de rotación. Si el campo magnético es uniforme y
estacionario, la trayectoria del electrón será
helicoidal.
Si además la velocidad y el campo magnético son
perpendiculares (senϕ=1), el electrón describirá
una circunferencia, de radio R, con una velocidad
tangencial v.
El equilibrio entre la fuerza magnética (evB) y la
fuerza centrífuga (
𝐦𝐞𝐯𝟐
𝐑
), nos permite calcular la
 Tubo a baja presión (1) lleno con helio a una
presión de 10-2 mmHg. Contiene en su interior
un cañón de electrones que origina el haz de
electrones. El haz de electrones deja una traza
visible en el tubo, porque algunos de los
electrones colisionan con los átomos de He, que
son excitados y entonces radian luz visible.
 Cañón de electrones (2) que emite un haz
fino de electrones al calentar su cátodo. Los
electrones son acelerados por un potencial
aplicado entre el cátodo y el ánodo. La grilla es
mantenida positiva con respecto al cátodo y
negativa con respecto al ánodo. Esto ayuda a
enfocar el haz de electrones.
 Bobinas de Helmoltz (3), que consiste en una
pareja de bobinas idénticas colocadas
paralelamente con una distancia entre ellas igual
al radio de cada una. De esta manera se consigue
un campo magnético muy uniforme en la zona
central. Las bobinas de Helmhotz de este
dispositivo tienen un radio y separación de 15 cm
y 130 vueltas cada una. El campo magnético
producido por las bobinas es proporcional a la
corriente que circula por ellas, cumpliendo
B=7.8x10-4I, donde el campo magnético B se
sobreentiende expresado en Teslas (T) y la
corriente I en Amperios (A).
 Panel de control del dispositivo (4). Todas sus
conexiones están rotuladas y son claras.
 Espejo con escala métrica (5), situada en la
parte de atrás de las bobinas de Helmholtz. Es
iluminada por la luz radiada desde el haz de
electrones. Sirve para medir el radio de la
trayectoria del haz sin error de paralaje.
Funcionamiento
Bobinas de Helmholtz
Cuando por las bobinas circula una corriente
directa y constante se crea un campo magnético
aproximadamente uniforme en su interior que se
puede calcular con la siguiente expresión:
Nμ0 I
B=
5 3/2
( ) R
4
donde:
N: Número de vueltas de la bobina de Helmholtz.
I: Corriente a través de las bobinas de Helmholtz
μo = 4πx10-7 T.m/A (Permeabilidad magnética del
espacio libre)
R: Radio de la bobina de Helmholtz
ΔU = ΔEk
Es decir,
1
qV = mv 2
2
donde,
V: diferencia de potencial entre el ánodo y el
cátodo (igual a la fuente de alimentación)
q,m: carga y masa de las partículas emitidas por
el filamento.
Partícula cargada entrando al campo magnético
Cuando las partículas salen del campo eléctrico
⃗ creado por las
entran al campo magnético B
⃗ m)
bobinas de Helmholtz. La fuerza magnética (F
que actúa sobre cada una de las partículas,
cuando entra con una velocidad v
⃗ en el campo
magnético
está
dada
por
⃗⃗⃗⃗⃗
⃗ . Si el vector de velocidad de la
Fm = qv
⃗ ×B
partícula es perpendicular al vector del campo
magnético, la magnitud de la fuerza magnética
será:
Fm = qvB
Bajo estas condiciones la partícula se moverá en
una
trayectoria
circular
de
radio
r,
experimentando una fuerza centrípeta de la
forma:
mv 2
Fc =
r
Quien obliga a la partícula a moverse en la
trayectoria circular es el campo magnético,
entonces la fuerza centrípeta en este caso es la
fuerza magnética, es decir.
Fc = Fm
Así, de las ecuaciones anteriores se obtiene:
2m
r2 = 2 V
B q
ANALISIS
Figura 4. Funcionamiento de e/m
Electrones acelerados por el campo eléctrico
Cuando se calienta el filamento por la fuente de
corriente alterna, este emite partículas, tal como
se evaporan las moléculas de un líquido al
calentarse. Este fenómeno se llama emisión
termoiónica. El potencial acelerador crea un
campo eléctrico entre el ánodo y el cátodo que
acelera las partículas emitidas por el filamento. Si
las partículas parten del reposo, al final de la
región de campo eléctrico tendrán una velocidad
(v), donde la energía cinética (ΔEk) ganada, será
igual a la energía potencial eléctrica perdida (ΔU):
Despues de conocer y entender el
funcionamiento de cada una de las partes de las
cuales consta el aparato de e/m se comenzó el
experimento el cual tenia como fin principal
comprender el papel de esta relación (e/m) y el
funcionamiento de los cañones electrónicos.
Para esto se requiere una ampolla esférica de
vidrio, llena de helio a una baja presión, la cual
posee en su interior un cañón
electrónico(instrumento a analizar). Este cañón
produce un haz de electrones (rayos catódicos).
Estos electrones en su trayecto colisionan con los
átomos del gas, excitándolos. La desescitación
inmediata da paso a la emisión de energía en
forma de luz. Esta cierta luminiscencia es la
región del gas alcanzada por la trayectoria de los
electrones.
pueda orientarse en cualquier ángulo (0
a 90 grados) con respecto al campo
magnético de las bobinas de Helmholtz.
Por lo tanto, se puede girar el tubo y
examinar la naturaleza vectorial de las
fuerzas magnéticas sobre partículas
cargadas en movimiento.
Este cañón electrónico es una disposición de
electrodos que libera, concentra y acelera
electrones, formando un haz que constituye un
rayo electrónico. La liberación se produce cuando
el material, en este caso el helio alcanza
suficiente temperatura como para que algunos de
sus electrones periféricos adquieran suficiente
energía como para “saltar”,. Esto se debe por lo
general y según la bibliografía consultada en un
filamento metálico (similar al de una bombilla de
alumbrado) que a la temperatura de
incandescencia a la que funciona produce este
efecto y actúa como cátodo. Otra placa próxima
cuyo potencial es superior al del cátodo,
constituye el ánodo, y atrae electrones
acelerándolos.
2.
La variación de voltaje y/o corriente
suministrada dando paso a nuevas
representaciones, espirales esferas de
mayor o menor radio e incluso en la
intensidad del haz de luz.
3.
Además de lo expuesto anteriormente
hay que tener en cuenta que la mayor
fuente de error en este experimento es
la velocidad de los electrones. En primer
lugar, la falta de uniformidad del campo
de aceleración causada por el agujero en
el ánodo provoca la velocidad de los
electrones a ser ligeramente inferior a su
valor teórico.
En cuanto a la geometría de las bobinas de
Helmholtz, donde el radio de las bobinas es igual
a su separación, provee de un campo magnético
uniforme. El campo magnético creado por las
bobinas es proporcional a las vueltas de alambres
de las bobinas.
Cabe destacar que para el correcto uso y
funcionamiento de este aparato se deben tener
en cuenta algunas características importantes
que fueron tenidas en cuenta en el momento de
la experimentación como lo son la diferente
graduación de cada uno de los equipos
Calentador:
6,3 VCA o VCC
Electrodos:
150 a 300 VDC
Bobinas de Helmholtz:
6-9 VDC (rizado debe ser
menos del 1%)
Inicialmente la trayectoria de colisión de los
electrones representada por el haz de luz
generado tenia un forma circular pero esta se
podía ver afectada por diferentes modificaciones
como:
1.
El giro de la esfera contenedora
permitiendo que el haz de electrones
BIBLIOGRAFÍA
1
TIPLER., Física para la ciencia y la tecnología., 5ta
edición., Editorial Reverte., Barcelona., 2002
2
SERWAY,J,R.,FISICAII.,3raEdición.,Thomson.,Méxi
co.,2003
3
http://www.heurema.com/PF19.htm
4
http://www.docentes.unal.edu.co/jdbaenad/doc
/ME/guion14-RelacionQMe.pdf
5
http://www.ucm.es/info/Geofis/practicas/prac2
5r.pdf