Flexión Pura
Anuncio

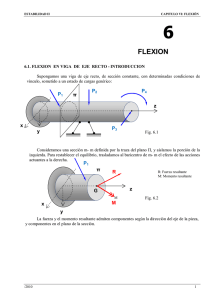
Juan Carlos Del Aguila Rodríguez A01370069 Flexión Pura Deformación Normal en la Flexión En elementos con un plano de simetría, sometidos a pares que actúan en ese mismo plano, las secciones transversales del elemento permanecen planas cuando éste es deformado. Un elemento sometido a flexión pura tiene una superficie neutra a lo largo de la cual las deformaciones y los esfuerzos normales son nulos y la deformación longitudinal normal εx varía linealmente con la distancia y la superficie neutra: 𝑦 𝜖𝑥 = − 𝜌 Esfuerzo Normal en el Rango Elástico Para elementos hechos de un material que cumple la Ley de Hooke se halló que el esfuerzo normal σx varía linealmente con la distancia al eje neutro. El eje neutro pasa por el centroide de la sección de un elemento sujeto a flexión pura. Siendo σm el esfuerzo máximo. 𝑦 𝜎𝑥 = − 𝜎𝑚 𝑐 Ecuación de la Flexión Elástica Para el esfuerzo máximo normal: 𝜎𝑚 = 𝑀𝑐 𝐼 Para el esfuerzo normal a cualquier distancia y desde el eje neutro: 𝜎𝑥 = − 𝑀𝑦 𝐼 En las cuales I es el momento de inercia de la sección transversal con respecto al eje neutro. Módulo Elástico de la Sección En las ecuaciones de la flexión elástica I y c sólo dependen de la geometría de la sección transversal, por lo tanto el módulo elástico de la sección estará dado por la siguiente ecuación. Como resultado se obtiene una expresión alterna para el esfuerzo normal máximo. 𝑆= 𝐼 𝑐 𝜎𝑚 = 𝑀 𝑆 Curvatura del Elemento La curvatura de un elemento es el inverso de su radio de curvatura, por lo tanto su curvatura será: 1 𝑀 = 𝜌 𝐸𝐼 Elementos Hechos de Varios Materiales En la flexión de elementos hechos de varios materiales con módulos de elasticidad diferentes, mientras las secciones transversales permanezcan, el eje neutro no pasa por el centroide de la sección transversal compuesta. Utilizando la relación entre los módulos de elasticidad diferente se puede obtener una sección transformada correspondiente a un elemento equivalente, hecho enteramente de un solo material. A partir de esto, se pueden usar los conceptos anteriores para determinar los esfuerzos en este elemento homogéneo transformado equivalente. Posteriormente se usa la relación entre los módulos de elasticidad para hallar los esfuerzos en la viga compuesta. Carga Axial Excéntrica Cuando un elemento está cargado excéntricamente en un plano de simetría, se reemplaza la carga excéntrica por un sistema fuerza-par localizado en la centroide de la sección transversal y luego se superponen los esfuerzos debidos a carga céntrica y al momento flexionante. 𝑃 𝑀𝑦 𝐴 𝐼 𝜎𝑥 = − En elementos con sección asimétrica la ecuación de flexión puede usarse siemre que el vector M se dirija a lo largo de uno de los ejes centroidales principales de la sección. Si es necesario se descompone M en componentes a lo largo de los ejes principales y se superponen los esfuerzos debidos a los pares componentes. 𝜎𝑥 = − 𝑀𝑧 𝑦 𝑀𝑦 𝑧 + 𝐼𝑧 𝐼𝑦 𝐼 La orientación del eje neutro se determina usando: tan 𝜑 = 𝐼𝑧 tan 𝜃 𝑦 Bibliografía: Beer, F.P., Johnston, E.R. (2013). Mecánica de Materiales. México: McGraw Hill.