Intervalos y contrastes
Anuncio

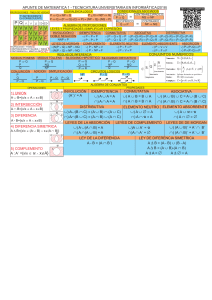
Métodos Estadı́sticos en la Ingenierı́a
INTERVALOS DE CONFIANZA
Intervalo de confianza para la media µ de una distribución normal con varianza σ 2 conocida:
n
σ
1X
σ
♦ X1 , ..., Xn m.a.s. de X ∼ N (µ, σ)
Ie = X ± zα/2 √
♦µ
b=X =
Xi ∼ N µ, √
n i=1
n
n
Intervalo de confianza para la media µ de una distribución normal con varianza desconocida:
2
Pn
n
2
X
2
X
−
n
X
1
S
i
i=1
2
♦µ
b = X ♦ σb2 = S =
Ie = X ± tn−1; α/2 √
Xi − X =
n − 1 i=1
n−1
n
√ X −µ
S2
√ ∼ tn−1
♦ X ∼ N µ, σ/ n y (n − 1) 2 ∼ χ2n−1 son independientes =⇒
σ
S/ n
Intervalo de confianza para la varianza σ 2 de una distribución normal con media µ conocida:
!
2
n
n nD2
nD2
1X
D2 X Xi − µ
2
2
2
b
,
Ie =
♦σ =D =
(Xi − µ)
∼ χ2n
♦n 2 =
χ2n; α/2 χ2n; 1−α/2
n i=1
σ
σ
i=1
Intervalo de confianza para la varianza σ 2 de una distribución normal con media desconocida:
!
2
n 2
2
2
X
X
−
X
(n − 1) S (n − 1) S
S
i
2
, 2
∼ χ2n−1
Ie =
♦ σb2 = S
♦ (n − 1) 2 =
2
χn−1; α/2 χn−1; 1−α/2
σ
σ
i=1
Intervalo de confianza para la diferencia de medias γ = µ1 − µ2 de dos distribuciones normales
independientes con varianzas σ12 y σ22 conocidas:
s
!
r 2
2
2
2
σ1 σ2
σ1 σ2
Ie =
X − Y ± zα/2
+
♦γ
b = X − Y ∼ N µ 1 − µ 2 ,
+
n1 n2
n1 n2
♦
X1 , . . . , Xn1 m.a.s. de X ∼ N (µ1 , σ1 )
;
Y1 , . . . , Yn2 m.a.s. de Y ∼ N (µ2 , σ2 )
X e Y independientes.
Intervalo de confianza para la diferencia de medias µ1 − µ2 de dos distribuciones normales independientes con varianzas desconocidas e iguales (σ12 = σ22 = σ 2 ):
s
2
2
Sp
Sp
(n1 − 1) S12 + (n2 − 1) S22
Ie = X − Y ± tn1 +n2 −2; α/2
♦ Sp2 =
+
n1
n2
n1 + n2 − 2
r
X −Y ∼N
(n1 + n2 − 2)
µ 1 − µ2 ,
2
2
σ
σ
+
n1 n2
Sp2
∼ χ2n1 +n2 −2
σ2
!
indep.
1
=⇒
X − Y − (µ1 − µ2 )
r
∼ tn1 +n2 −2
1
1
Sp
+
n1 n2
Intervalo de confianza para la diferencia de medias γ = µ1 − µ2 de dos distribuciones normales
independientes con varianzas desconocidas y distintas (σ12 6= σ22 ):
r
X − Y ± tf ; α/2
Ia =
S12 S22
+
n1
n2
!
2
♦f =
(S12 /n1 + S22 /n2 )
X −Y −γ a
r 2
−
2
♦
≈ tf
S1
S22
(S12 /n1 )
(S22 /n2 )2
+
+
n1
n2
n1 + 1
n2 + 1
2
Intervalo de confianza para el cociente de varianzas β = σ12 /σ22 de dos distribuciones normales
independientes con medias µ1 y µ2 conocidas:
Ie =
D12 /D22
D12 /D22
,
Fn1 , n2 ; α/2 Fn1 , n2 ; 1−α/2
χ2n1
D2 /σ 2
n
♦ 12 12 ∼ 21 ≡ Fn1 ,n2
χn2
D2 /σ2
n2
D2
♦ βb = 12
D2
Intervalo de confianza para el cociente de varianzas β = σ12 /σ22 de dos distribuciones normales
independientes con medias desconocidas:
S12 /S22
Ie =
S12 /S22
,
χ2n1 −1
S 2 /σ 2
n −1
♦ 12 12 ∼ 12
≡ Fn1 −1,n2 −1
χn2 −1
S2 /σ2
n2 − 1
S2
♦ βb = 12
S2
Fn1 −1, n2 −1; α/2 Fn1 −1, n2 −1; 1−α/2
Intervalo de confianza para la diferencia media µD = µX −µY de datos apareados (Xi , Yi ) i = 1, ..., n.
Se supone que D = X − Y ∼ N (µD , σD ) con σD desconocida:
Ie =
SD
D ± tn−1; α/2 √
n
D − µD
√ ∼ tn−1 ;
SD / n
n
♦µ
bD = D =
Di = Xi − Yi i = 1, ..., n;
1X
Di
n i=1
n
2
2
♦ σc
D = SD =
2
1 X
Di − D
n − 1 i=1
D1 , . . . , Dn m.a.s. de D = X − Y ∼ N (µD , σD )
Intervalos de confianza para el parámetro p de una distribución binomial X ∼ B(n, p), n grande:
r
Ia =
pb ± zα/2
pb (1 − pb)
n
s
Ia =
sen2
arcsen
2
zα/2
zα/2
nb
p + 3/8
± √
n + 3/4
2 n
♦ X ∼ B(n, p) ≈ N np,
Ie =
p
np(1 − p)
2
zα/2
nb
p+
± zα/2 nb
p (1 − pb) +
2
4
Ia =
2
n
+
z
α/2
!
!!
♦ pb =
s
a
s
♦ arcsen
X
No total de éxitos
= o
n
N total de pruebas
X + 3/8 a
≈N
n + 3/4
√
1
arcsen p, √
2 n
(X + 1) F2(X+1), 2(n−X); α/2
X
,
X + (n − X + 1) F2(n−X+1), 2X; α/2 (n − X) + (X + 1) F2(X+1), 2(n−X); α/2
2
Intervalo de confianza para la diferencia de parámetros w = p1 − p2 de dos distribuciones binomiales
independientes X1 ∼ B(n1 , p1 ) y X2 ∼ B(n2 , p2 ) con n1 y n2 grandes:
r
pb1 (1 − pb1 ) pb2 (1 − pb2 )
X1 X2
Ia = (b
p1 − pb2 ) ± zα/2
+
♦w
b = pb1 − pb2 =
−
n1
n2
n1
n2
p
a
♦ X1 − X2 ≈ N n1 p1 − n2 p2 , n1 p1 (1 − p1 ) + n2 p2 (1 − p2 )
b grande):
Intervalos de confianza para el parámetro λ de una distribución de Poisson X ∼ P (λ), (nλ
s
q
2
2
b
zα/2
z
zα/2 4λ
α/2
b ± zα/2 λ/n
b
b+
Ia = λ
Ia = λ
±
+ 2
2n
2
n
n
(
Ia = máx 0,
♦
n
X
2
zα/2
3
b
− √
λ+
8n 2 n
r
!)2 (r
2
zα/2
3
b
+ √
λ+
8n 2 n
,
√ a
Xi ∼ P (nλ) ≈ N nλ, nλ
)2
p
a
b=X≈
♦λ
N λ, λ/n
i=1
λ grande
♦ X ∼ P (λ) =⇒
p
Ie =
a
X + 3/8 ≈ N
√
λ, 1/2
!
♦
χ22K; 1−α/2 χ22K+2; α/2
,
2n
2n
q
a
b + 3/8 ≈
N
nλ
♦K=
n
X
√
nλ, 1/2
Xi
i=1
Intervalos de confianza para la diferencia de parámetros δ = λ1 − λ2 de dos distribuciones de Poisson
b 1 y n2 λ
b2 grandes):
independientes X ∼ P (λ1 ) e Y ∼ P (λ2 ) , (n1 λ
p
s
a
b
b
b
λ
=
X
≈
N
λ
,
λ
/n
1
1
1
1
b1 − λ
b2 ± zα/2 λ1 + λ2
b1 −λ
b2
p
Ia = λ
♦ δb = λ
♦
a
b2 = Y ≈
λ
n1 n2
N λ2 , λ2 /n2
Intervalo de confianza para el parámetro λ de una distribución exponencial X ∼ Exp (λ):
!
n
X
χ22n; 1−α/2 χ22n; α/2
2n 1
,
Ie =
♦ 2nλX = 2λ
Xi ∼ G
,
≡ χ22n
2
2
2nX
2nX
i=1
b= n−1
♦λ
n
P
Xi
♦ Si θ = E [X] = 1/λ =⇒ θb = X
i=1
Intervalo de confianza para el cociente de parámetros ω = λ1 /λ2 de dos distribuciones exponenciales
independientes X ∼ Exp (λ1 ) e Y ∼ Exp (λ2 ) :
Ie =
Y /X F2n1 ,2n2 ; 1−α/2 , Y /X F2n1 , 2n2 ; α/2
2n1 λ1 X = 2λ1
2n2 λ2 Y = 2λ2
n1
P
i=1
n2
P
i=1
Xi ∼ G(n1 , 1/2) ≡
χ22n1
Yi ∼ G(n2 , 1/2) ≡ χ22n2
3
♦ω
b=
Y
X
χ22n1
λ1 /λ2
2n
indep. =⇒
∼ 2 1 ≡ F2n1 , 2n2
χ
Y /X
2n2
2n2
Métodos Estadı́sticos en la Ingenierı́a
CONTRASTES DE HIPÓTESIS PARAMÉTRICAS
Contrastes de hipótesis para la media µ de una distribución normal con varianza σ 2 conocida:
H 0 : µ = µ0
H1 : µ 6= µ0
R = | Z |≥ zα/2
H 0 : µ ≤ µ0
H1 : µ > µ0
♦Z=
R = {Z ≥ zα }
X − µ0 H0
√ ∼ N (0, 1)
σ/ n
H 0 : µ ≥ µ0
H1 : µ < µ0
R = {Z ≤ −zα }
Contrastes de hipótesis para la media µ de una distribución normal con varianza desconocida:
H 0 : µ = µ0
H1 : µ 6= µ0
R = | T |≥ tn−1; α/2
♦T =
H 0 : µ ≤ µ0
H1 : µ > µ0
R = {T ≥ tn−1; α }
X − µ0 H0
√ ∼ tn−1
S/ n
H 0 : µ ≥ µ0
H1 : µ < µ0
R = {T ≤ −tn−1; α }
Contrastes de hipótesis para la varianza σ 2 de una distribución normal con media µ conocida:
H0 : σ = σ0
H1 : σ 6= σ0
n
o
R= W ∈
/ χ2n; 1−α/2 , χ2n; α/2
H0 : σ ≤ σ0
H1 : σ > σ0
R= W ≥
χ2n; α
♦W =n
D2 H0 2
∼ χn
σ02
H0 : σ ≥ σ0
H1 : σ < σ0
R = W ≤ χ2n; 1−α
Contrastes de hipótesis para la varianza σ 2 de una distribución normal con media desconocida:
H0 : σ = σ0
H1 : σ 6= σ0
H0 : σ ≤ σ0
H1 : σ > σ0
n
o
2
2
R= W ∈
/ χn−1; 1−α/2 , χn−1; α/2
R= W ≥
χ2n−1; α
♦ W = (n − 1)
H0 : σ ≥ σ0
H1 : σ < σ0
S 2 H0 2
∼ χn−1
σ02
R = W ≤ χ2n−1; 1−α
Contrastes para la diferencia de medias γ = µ1 − µ2 de dos distribuciones normales independientes
con varianzas σ12 y σ22 conocidas:
H0 : µ1 − µ2 = γ0
H1 : µ1 − µ2 6= γ0
H0 : µ1 − µ2 ≤ γ0
H 1 : µ1 − µ2 > γ 0
R = | Z |≥ zα/2
X − Y − γ0 H0
♦Z= r 2
∼ N (0, 1)
σ1 σ22
+
n1 n2
H0 : µ1 − µ2 ≥ γ0
R = {Z ≤ −zα }
H 1 : µ1 − µ2 < γ 0
R = {Z ≥ zα }
4
Contrastes para la diferencia de medias γ = µ1 − µ2 de dos distribuciones normales independientes
con varianzas desconocidas e iguales (σ12 = σ22 = σ 2 ):
H0 : µ1 − µ2 = γ0
H1 : µ1 − µ2 6= γ0
H0 : µ1 − µ2 ≤ γ0
H 1 : µ1 − µ2 > γ 0
R = | T |≥ tm; α/2
X − Y − γ0 H0
r
♦T =
∼ tm ; m = n1 + n2 − 2
1
1
Sp
+
n1 n2
H0 : µ1 − µ2 ≥ γ0
R = {T ≤ −tm; α }
H 1 : µ1 − µ2 < γ 0
R = {T ≥ tm; α }
Contrastes para la diferencia de medias γ = µ1 − µ2 de dos distribuciones normales independientes
con varianzas desconocidas y distintas (σ12 6= σ22 ):
H0 : µ1 − µ2 = γ0
H1 : µ1 − µ2 6= γ0
H0 : µ1 − µ2 ≤ γ0
H 1 : µ1 − µ2 > γ 0
R ' | T |≥ tf ; α/2
X − Y − γ0 H0
♦T = r 2
≈ tf
S1
S22
+
n1
n2
H0 : µ1 − µ2 ≥ γ0
R ' {T ≤ −tf ; α }
H 1 : µ1 − µ2 < γ 0
R ' {T ≥ tf ; α }
Contrastes para el cociente de varianzas β = σ12 /σ22 de dos distribuciones normales independientes
con medias µ1 y µ2 conocidas:
H0 : β = β0
H1 : β 6= β0
H0 : β ≤ β0
H 1 : β > β0
R= F ∈
/ Fn1 ,n2 ; 1−α/2 , Fn1 ,n2 ; α/2
R = {F ≥ Fn1 ,n2 ; α }
♦F =
H0 : β ≥ β0
H 1 : β < β0
D12 /D22 H0
∼ Fn1 ,n2
β0
R = {F ≤ Fn1 ,n2 ; 1−α }
Contrastes para el cociente de varianzas β = σ12 /σ22 de dos distribuciones normales independientes
con medias desconocidas:
S 2 /S 2 H
H0 : β = β0
R= F ∈
/ Fn1 −1,n2 −1; 1−α/2 , Fn1 −1,n2 −1; α/2
♦ F = 1 2 ∼0 Fn1 −1,n2 −1
H1 : β 6= β0
β0
H0 : β ≤ β0
H 1 : β > β0
R = {F ≥ Fn1 −1,n2 −1; α }
H0 : β ≥ β0
H 1 : β < β0
R = {F ≤ Fn1 −1,n2 −1; 1−α }
Contrastes para la diferencia de las medias µD = µX −µY de dos distribuciones apareadas. Se supone
que D = X − Y ∼ N (µD , σD ) con σD desconocida:
H 0 : µD = µ0
H1 : µD 6= µ0
H 0 : µD ≤ µ0
H 1 : µD > µ 0
R = | T |≥ tn−1; α/2
♦T =
R = {T ≥ tn−1; α }
5
D − µ0 H0
√ ∼ tn−1
SD / n
H 0 : µD ≥ µ0
H 1 : µD < µ 0
R = {T ≤ −tn−1; α }
Contrastes para el parámetro p de una distribución binomial X ∼ B(n, p) con n grande:
H0
pb − p0
H0 : p = p 0
♦Z= p
≈ N (0, 1)
R ' | Z |≥ zα/2
H1 : p 6= p0
p0 (1 − p0 ) /n
H0 : p ≤ p 0
H0 : p ≥ p 0
R ' {Z ≥ zα }
R ' {Z ≤ −zα }
H1 : p > p0
H1 : p < p0
Contrastes sobre la relación entre los parámetros p1 y p2 de dos distribuciones binomiales independientes X1 ∼ B(n1 , p1 ) y X2 ∼ B(n2 , p2 ); ( n1 y n2 grandes; pb = (X1 + X2 ) / (n1 + n2 ) ):
H0
pb1 − pb2
H0 : p 1 = p 2
♦Z= s
≈ N (0, 1)
R ' | Z |≥ zα/2
H1 : p1 6= p2
1
1
+
pb (1 − pb)
n1 n2
H0 : p 1 ≤ p 2
H0 : p 1 ≥ p 2
R ' {Z ≥ zα }
R ' {Z ≤ −zα }
H1 : p 1 > p 2
H1 : p 1 < p 2
Contrastes para
H0 :
H1 :
H0 :
H1 :
b grande):
el parámetro λ de una distribución de Poisson X ∼ P (λ), (nλ
λ = λ0
λ 6= λ0
R ' | Z |≥ zα/2
λ ≤ λ0
λ > λ0
R ' {Z ≥ zα }
b − λ0 H0
λ
♦Z= p
≈ N (0, 1)
λ0 /n
H0 : λ ≥ λ0
R ' {Z ≤ −zα }
H1 : λ < λ 0
Contrastes sobre la relación entre los parámetros λ1 y λ2 de dos
distribuciones
de Poisson indepenb
b
b
b
b
dientes X ∼ P (λ1 ) e Y ∼ P (λ2 ); ( n1 λ1 y n2 λ2 grandes; λ = n1 λ1 + n2 λ2 / (n1 + n2 ) ):
H 0 : λ1 = λ2
H1 : λ1 6= λ2
H 0 : λ1 ≤ λ2
H 1 : λ1 > λ 2
R ' | Z |≥ zα/2
♦Z= q
R ' {Z ≥ zα }
b1 − λ
b2
λ
H0
≈ N (0, 1)
b 1 + λ/n
b 2
λ/n
H 0 : λ1 ≥ λ 2
H1 : λ1 < λ 2
R ' {Z ≤ −zα }
Contrastes para el parámetro λ de una distribución exponencial X ∼ Exp(λ):
o
n
n
P
H0 : λ = λ0
H
♦ W = 2nλ0 X = 2λ0
Xi ∼0 χ22n
R= W ∈
/ χ22n; 1−α/2 , χ22n; α/2
H1 : λ 6= λ0
i=1
H 0 : λ ≤ λ0
H 0 : λ ≥ λ0
2
R = W ≤ χ2n; 1−α
R = W ≥ χ22n; α
H1 : λ > λ 0
H1 : λ < λ 0
Contrastes para el cociente de parámetros ω = λ1 /λ2 de dos distribuciones exponenciales independientes X ∼ Exp (λ1 ) e Y ∼ Exp (λ2 ) :
ω0 H0
H0 : λ1 /λ2 = ω0
R= F ∈
/ F2n1 ,2n2 ; 1−α/2 , F2n1 ,2n2 ; α/2
♦F =
∼ F2n1 ,2n2
H1 : λ1 /λ2 6= ω0
Y /X
H0 : λ1 /λ2 ≤ ω0
H0 : λ1 /λ2 ≥ ω0
R = {F ≥ F2n1 ,2n2 ; α }
R = {F ≤ F2n1 ,2n2 ; 1−α }
H1 : λ1 /λ2 > ω0
H1 : λ1 /λ2 < ω0
6