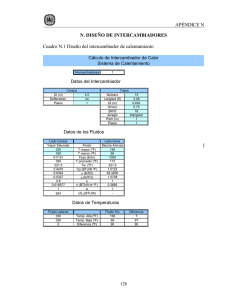
APUNTE DE MATEMATICA 1 - TECNICATURA UNIVERSITARIA EN INFORMÁTICA(2018)
FELIX DARIO SABATINI
CONDICIONALES ASOCIADOS
CONTRARECIPROCO
P Ú Q º N(P Û Q) DIRECTO
P Þ Q º NP Ú Q
P=ANTECEDENTE
º
NQ Þ NP
PÞQ
Q=CONSECUENTE
P Û Q º (P Þ Q)Ù(Q Þ P) º (NP Ú Q)Ù(NQ Ú P)
CONTRARIO
RECIPROCO
_ ÞÛ
P Q Ù Ú Ú
º NP Þ NQ
QÞP
ALGEBRA DE PROPOSICIONES
V V V V F V V LEYES Y PROPIEDADES (SIMPLIFICAR EXPRESIÓN)
VERSION ONLINE
DISTRIBUTIVA
ASOCIATIVA
CONMUTATIVA
IDEMPOTENCIA
INVOLUCIÓN
O
V F F V V F F
DOBLE NEGACIÓN
Ú) P Ú Q º Q Ú P Ú)PÚ(QÚR) º (PÚQ)ÚR Ú)PÚ(QÙR) º (PÚQ)Ù(PÚR)
Ú) P Ú P º P
F V F V V V F
NNP º P
Ù) P Ù Q º Q Ù P Ù)PÙ(QÙR) º (PÙQ)ÙR Ù)PÙ(QÚR) º (PÙQ)Ú(PÙR)
Ù) P Ù P º P
F F F F F V V LEYES DE MORGAN COMPLEMENTO ELEMENTO NEUTRO ELEMENTO ABSORVENTE ABSORCIÓN
TAUTOLOGIA = TODO V
Ú) P Ú F º P
Ú) PÙ(PÚQ) º P
Ú) P Ú NP º V
Ú)N(P Ú Q) º NP Ù NQ
Ú) P Ú V º V
CONTRADICIÓN O FALASIA = TODO F
Ù) P Ù V º P
Ù) PÚ(PÙQ) º P
Ù) P Ù NP º F
Ù)N(P Ù Q) º NP Ú NQ
Ù) P Ù F º F
CONTINGENCIA = MEZCLA DE V Y F
REGLAS DE INFERENCIA
CONJUNTOS NUMERICOS
MODUS PONENS MODUS TOLLENS SILOGISMO HIPOTETICO SILOGISMO DISYUNTIVO
PÞQ
PÞQ
PÞQ
PÚQ
PÚQ
NQ
P
NP
NQ
QÞR
NP
Q
Q
P
PÞR
CIRCUITOS LOGICOS
CONJUNCIÓN ADICIÓN SIMPLIFICACIÓN
PÚQ
NP
PÙQ
P
P
P
Q
PÙQ PÙQ
NP
P
Q
Q
PÚQ
P
Q
PÙQ
ALGEBRA DE CONJUNTOS
EQUIVALENCIA LOGICA
PROPOSICIONES - TABLA DE VERDAD
PROPIEDADES
OPERACIONES
U
1) UNION
A
B
A È B={x/x Î A Ú xÎB}
2) INTERSECCIÓN
U
A
B
A Ç B={x/x Î A Ù xÎB}
3) DIFERENCIA
U
A
B
A - B={x/x Î A Ù xÏB}
4) DIFERENCIA SIMETRICA
A D B={x/x Î (A È B) Ù xÏ(A Ç B)}
U
A
U
5) COMPLEMENTO
A : A´ ={x/x Î U Ù xÏA}
A
B
INVOLUCIÓN
(A´)´ = A
IDEMPOTENCIA
È) A È A = A
Ç) A Ç A = A
CONMUTATIVA
È) A È B = B È A
Ç) A Ç B = B Ç A
ASOCIATIVA
È) (A È B) È C = A È (B È C)
Ç) (A Ç B) Ç C = A Ç (B Ç C)
DISTRIBUTIVA
ELEMENTO NEUTRO
È) AÈ(B Ç C) = (A È B) Ç (A È C)
È) A È Æ = A
Ç) AÇ(B È C) = (A Ç B) È (A Ç C)
Ç) A Ç U = A
LEYES DE LA ABSORCIÓN
È) A È(A Ç B) = A
Ç) A Ç(A È B) = A
LEYES DE COMPLEMENTO
È)A È A´ = U
Ç)A Ç A´ = Æ
LEY DE LA DIFERENCIA
A - B = (A Ç B´)
ELEMENTO ABSORBENTE
È) A È U = U
Ç) A Ç Æ = Æ
LEYES DE DE MORGAN
È) (A È B)´ = A´ Ç B´
Ç) (A Ç B)´ = A´ È B´
LEY DE DIFERENCIA SIMETRICA
A D B = (A - B) È (B - A)
A D B = (A È B)-(A Ç B)
ADA=Æ
ADÆ=A