Laboratorio 1: Introducción
Anuncio

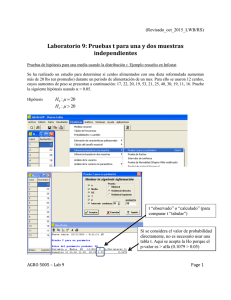
Laboratorio 1 – rev. 2014 - LWB AGRO 5005: BIOMETRÍA LABORATORIOS Contents Laboratorio 1: Introducción ............................................................................................................ 2 Laboratorio 2: Manejo de datos – Gráficos I .................................................................................. 6 Laboratorio 3: Resumen gráfico de la información II .................................................................... 9 Laboratorio 4: Estadísticos descriptivos ....................................................................................... 11 Laboratorio 5: Probabilidad y Distribución Binomial .................................................................. 15 Laboratorio 6: Distribución Normal ............................................................................................. 20 Laboratorio 7: Distribuciones Muestrales ..................................................................................... 23 Laboratorio 8: Intervalos de Confianza y Pruebas de Hipótesis ................................................... 25 Laboratorio 9: Pruebas t para una y dos muestras independientes ............................................... 27 Laboratorio 10: Pruebas t para muestras pareadas ........................................................................ 30 Laboratorio 11: Análisis de la Varianza ....................................................................................... 33 Laboratorio 12: Tablas de Contingencia ....................................................................................... 35 Laboratorio 13: Regresión y correlación lineal ............................................................................ 37 Laboratorio 14: Diseño en bloques completos aleatorizados ....................................................... 39 Laboratorio 1 – rev. 2014 - LWB Laboratorio 1: Introducción ( x a )( xb ) x a b ( xy )a x a y a ( x a ) / ( x b ) x a b n ! n(n 1)(n 2) 1 ( x a )b x ab 0! 1 x1 x x0 1 (1) Simplifique y evalúe las siguientes expresiones: a. 102 x 105 = __________ b. (106)/(105) = ________ c. 23 x 32 = __________ 3 3 d. (3 ) = ____________ e. 7! = _______________ f. 2-5 x 23 = __________ g. 42/22 = ___________ h. (5 x 3)2 = __________ 2 2 i. (0.01 )/(0.001 ) = ________ j. (6!)/(3!) = __________ (2) Notación sumatoria. Escriba los sumandos de cada una de las sumas siguientes: 4 X Ejemplo: i 1 i X1 X 2 X 3 X 4 4 a. ( X i a) i 1 6 X Y b. i 1 i i 3 c. X j 1 j 4 d. a X i i 1 (3) Para la muestra de tamaño n=5 presentada abajo, evalúe las siguientes sumatorias. Use las funciones en su calculadora que le permitan simplificar los cálculos. X1 119, X2 98, X3 79, X4 89, X5 95 5 a. X i 1 i 5 b. X i 1 i /5 Laboratorio 1 – rev. 2014 - LWB 5 c. (X i 1 i 96) i 96)2 5 d. (X i 1 5 e. X 2 i i 1 ( X i ) 2 / 5 (4) Identifique las posiciones en la matriz y evalúe las sumatorias. Recuerde que el primer subíndice indica la fila, y el segundo la columna. (Ejemplo: en la fila 2 y columna 3, el valor numérico 5 puede ser identificado como X 2,3 ) 1 5 2 1 4 a. X i ,2 i 1 3 7 3 2 2 5 3 1 3 6 4 2 (ayuda: los posibles valores de Xi2 son X12, X22, X32 y X42) 4 b. X j 1 4, j 2 1, j 4 c. X j 1 (ayuda: elevar al cuadrado cada observación antes de sumar las observaciones) 4,4 d. i 1, j 1 X i, j 4 e. X i 1 i ,i Laboratorio 1 – rev. 2014 - LWB (5) Cierto tipo de desperdicios contaminantes (como excrementos de ganado lechero) puede traer problemas serios de contaminación por nitratos a los acuíferos. Para estudiar este problema se escogieron 80 muestras aleatorias de agua en los acuíferos del área norte de Puerto Rico. a. b. c. d. Identifique la población de interés. Identifique la muestra. ¿Qué características de la población le interesaría medir para estudiar el problema? ¿Cómo resumiría la información obtenida en la muestra? (6) Se desea estudiar la capacidad respiratoria (VO2MAX) de estudiantes universitarios. Para ello se escogen 100 estudiantes al azar en el RUM y a cada uno se le medirá la capacidad respiratoria. Además se registrará el sexo, la edad, el nivel de actividad física, y otras características. a. b. c. d. Identifique la población de interés. Identifique la muestra. ¿Cómo podríamos seleccionar esta muestra? ¿Qué preguntas de investigación podrían formularse con la información disponible en los estudiantes estudiados en la muestra? Infostat es un programa en español que permite realizar la mayoría de los cálculos estadísticos, tiene capacidades gráficas bastante avanzadas y un manejo de datos similar a otros programas de bases de datos. La mayoría de los cálculos de resumen y de los gráficos también pueden realizarse en Excel, pero los análisis estadísticos normalmente no se pueden hacer en Excel sin programas adicionales. Utilizando el menú “Archivo, Nueva tabla”, entre las 4 columnas de datos (incluyendo “árbol”) que se encuentran en la próxima página. Guarde sus datos en un “jump drive” utilizando la opción de “Archivo, Guardar tabla como”. Vamos a utilizar estos datos para hacer varios ejercicios durante el día de hoy y en los próximos laboratorios. Los datos representan una muestra aleatoria simple de 40 árboles de café. Las variables medidas incluyen presencia de roya (una enfermedad), altura (m) y diámetro (cm) de cada árbol. Después de entrar los datos, favor continuar con los próximos ejercicios en InfoStat: (7) Infostat nos provee la opción de crear una nueva variable que se define utilizando una o más variables previamente definidas. Por ejemplo, digamos que queremos transformar los datos de altura (m) a altura (pies). En el menú “Datos, Fórmulas” se entra el nombre de la nueva variable (digamos Altura_pies), y se define Altura_pies en términos de una o más variables ya existentes (una lista de variables aparecerá en una ventanilla a la derecha; operadores aparecerán en una ventana). Después de definir la fórmula y oprimir “calcular”, InfoStat colocará los valores de Altura_pies en una nueva columna. Utilice el menú “Datos, Fórmula” para transformar altura en metros a altura en pies (1m=3.28ft). (8) Nos interesa categorizar nuestros árboles de acuerdo con los siguientes 4 categorías de diámetros: hasta 5cm, más de 5cm hasta 9cm, más de 9cm hasta 12cm, más de 12cm. Seleccione la columna “Diámetro” y haga un “click” derecho. Usando el menú “Categorizar, Asignar categorías por intervalos, Personalizado”, crear 4 clases de diámetro. Defina el límite Laboratorio 1 – rev. 2014 - LWB superior (LS) de cada clase. Por ejemplo, el LS1 es 5. InfoStat automáticamente apuntará el LS de la última clase. En “Editar categorías” escriba las descripciones correspondientes. (No es recomendable utilizar la opción de dejar las categorías definidas como “C1”, etc. Varios meses después de categorizar sus datos es muy posible que no recuerde su sistema de clasificación! (9) Usando el menú “datos, ordenar”, contar cuántos árboles están enfermos. (10) Seleccione todas las filas de datos enfermo = sí. Utilizando un “click” derecho, se desactivan estos casos. Ahora mueva su cursor a otra parte de la página. Los datos sombrados en color rosado no pueden ser utilizados en ningún análisis hasta que no sean archivados nuevamente. Repita el proceso para reactivar los datos (verifique que se quitó el color rosado) Árbol 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 Enfermo no si no no no no si no no no si no no no no no no no si no no no no no no no no no no si si no si si no no si no no si Altura 3.17 3.27 2.60 2.24 3.58 2.89 3.00 3.74 2.83 2.13 2.83 4.23 3.24 3.22 2.23 2.62 3.31 2.95 2.48 2.59 2.61 2.71 2.61 4.96 2.05 3.97 2.73 3.09 3.48 2.57 3.17 2.34 3.23 3.62 3.55 2.67 3.41 2.43 0.96 2.67 5 Diámetro 11 9 10 18 6 14 11 9 11 8 6 10 12 8 8 12 11 5 8 7 13 2 5 9 14 15 13 10 12 8 5 10 7 11 5 6 10 14 10 Laboratorio 2 – rev. 2014 - LWB Laboratorio 2: Manejo de datos – Gráficos I Planes de muestreo Para cada uno de los siguientes planes de muestreo, identifique el nombre del plan de muestreo que se está usando e indique cuál es la unidad (o unidades) de muestreo. 1. Se desea estimar el daño por roya (una enfermedad) de café en una finca. Para ello se lleva a cabo el siguiente plan de muestreo: Caminando a lo largo de la primera hilera en la finca, se elige aleatoriamente un árbol entre los primeros 20 árboles. Luego de realizar esta evaluación se continúa caminando y se evalúa cada árbol ubicado en la posición número 20 (es decir, se cuentan los árboles a partir del que se ha evaluado y se evalúa cada 20 árboles). Como hay aproximadamente 600 árboles en la finca, se espera muestrear alrededor de 30 árboles. A cada árbol se le realiza una evaluación visual del daño por roya en las hojas (escala 1 a 5, con 1 representando “sin daño” y 5 representando “mayoría de hojas completamente dañadas”). 2. Para estudiar la prevalencia de mastitis (definida aproximadamente como el porcentaje de animales enfermos) en hatos lecheros en Puerto Rico se eligen 15 vaquerías aleatoriamente de la lista de vaquerías registradas en el Departamento de Agricultura. En cada vaquería se examinan 12 vacas aleatoriamente elegidas. 3. En un estudio de capacidad de secuestro de carbono por bosques secundarios, se va a determinar la altura y el diámetro de todos los árboles en parcelas escogidas aleatoriamente del área central de Puerto Rico. En cada una de las tres zonas ecológicas identificadas en mapas se elegirán al azar parcelas de 0.5 hectáreas, y se registrarán las variables de interés en todos los árboles de la parcela. La cantidad de parcelas a elegir en cada zona ecológica es proporcional al área que esa zona representa respecto al área total de la zona central de Puerto Rico. Manejo de datos en Infostat Para manejar datos en Infostat se puede trabajar con el menú Datos. Este menú permite crear nuevas filas, insertar o eliminar filas, activar/desactivar casos (filas), crear/insertar/eliminar columnas, poner etiquetas (nombres a las columnas), definir el tipo de datos en una columna, la cantidad de decimales a mostrar, ordenar, crear categorías, transformar y aplicar fórmulas. En este laboratorio vamos a trabajar con los datos de café entrados en la última clase y con otros conjuntos de datos que ya están en Infostat. Los archivos que ya están en Infostat se acceden con el menú “Archivo, abrir datos de prueba”. Para usar el menú de gráficos debemos tener la tabla de datos abierta. Hay dos ventanas relacionadas: Herramientas gráficas y Gráficos. Vamos a preparar distintos gráficos con los datos provistos y aprenderemos las herramientas básicas sobre los ejemplos. Es muy importante que practiquen distintas alternativas, opciones, etc. hasta lograr el gráfico deseado. Una vez que está el gráfico completo podemos hacer copia del mismo para ponerlo, por ejemplo, en Word o Laboratorio 2 – rev. 2014 - LWB PowerPoint. En el manual de Infostat (menú Ayuda>Manual) se describen todas las opciones gráficas disponibles. Es importante recordar que Infostat solamente guarda los cambios efectuadas en la tabla de datos abierta, es decir, no guarda ni gráficos ni la salida mostrada en la ventana “Resultados”. Si queremos guardar los gráficos tenemos dos opciones: o los copiamos en un documento (por ejemplo en Word), o los guardamos como gráficos de Infostat. La última opción nos permitirá cambiarlos en el futuro, mientras que si queremos cambiar un gráfico que ya está pegado en Word debemos rehacerlo en Infostat. 4. Realice un gráfico de barras para ver la altura promedio de árboles sanos y enfermos (datos de café usados en el laboratorio 1). Use como variable a graficar la altura (en metros), y como criterio de clasificación la variable enfermo. Las opciones que puede usar son “media, medidas de confianza, ninguna”. a. Considere la salida original (sin arreglar las escales, etc.,): i. ¿Qué estadística está representada por la altura de las barras? ii. ¿Parece haber una diferencia en la altura promedio de árboles enfermos y no enfermos? b. Cambie la escala de Y a un mínimo de 0 y un máximo de 3.5. Arregle los “ticks” (divisiones en la escala) y los decimales. Haga los otros arreglos necesarios para que se pueda apreciar bien lo que se quiere mostrar. i. Después de realizar los cambios, ¿Parece haber una diferencia en la altura promedio de árboles enfermos y no enfermos? 5. Grafique los siguientes datos, referidos a la distribución porcentual del gasto de alimento anual en distintas categorías. (% = porcentaje de los gastos anuales en alimentos). Realice un gráfico de barras y luego un gráfico de sectores. Para el gráfico de barras, la “variable a graficar” es “%” y el “criterio de clasificación” es “alimento” (las categorías en el eje X). Para el gráfico de sectores entramos “alimento” en la ventanilla de “clases (sectores de la torta)” y “%” en “frecuencia”. Haga los otros arreglos necesarios para que se pueda apreciar bien lo que se quiere mostrar. Para arreglar las barras en orden de mayor a menor: en el eje X selecciona la categoría que desea mover, y utilice “Ctrl + flecha” para mover la categoría al lugar deseado. ¿Qué gráfico le gusta más? Categoría Productos lácteos Cereal y panificados Bebidas sin alcohol Pescados y aves Frutas y vegetales Carne Otras % 13.4 12.6 8.9 7.5 15.6 24.5 17.5 Laboratorio 2 – rev. 2014 - LWB 6. Los siguientes datos representan los gastos (en dólares/mes) de familias urbanas y rurales en distintos rubros. Familia Urbana Rural alimentación serv. e imp. educación otros 300 500 90 50 120 50 100 100 a. Para las familias rurales y urbanas, calcule (a mano) el porcentaje de los gastos mensuales (totales) que se debe a los costos de cada categoría de gastos. b. A mano, haga un gráfico de sectores para las familias urbanas mostrando los gastos proporcionales en los distintos. Haga otro gráfico para familias rurales. Compare sus gráficos con gráficos de sectores hechos con InfoStat (ayuda: las categorías están en columnas, “familia” en “criterios de clasificación”) c. Realice un gráfico de barras apiladas (con familia en “criterios de clasificación”), seleccionando la opción de “apilar proporciones”. Como compara la información presentada en este gráfico con la de la parte b? Los archivos para los siguientes ejercicios se encuentran en el menú “Archivo, abrir datos de prueba”: 7. Con el objetivo de estudiar la relación entre el peso (Y) y el perímetro (X) de cabezas de ajo, prepare los diagramas de dispersión indicados utilizando los datos de Ajoblanc (datos del perímetro (cm) y el peso (g) de la cabeza de 1600 ajos de cosechas de 1998 y 1999 [Fuente: Software InfoStat]). a. Haga un gráfico con ambos años juntos. ¿Hay una relación entre el perímetro y el peso? Si su respuesta es sí, describa la relación. b. Utilizando la opción de “particiones”, haga un gráfico que identifique el año con colores diferentes. ¿Hay diferencias entre años? 8. Utilizando el conjunto de datos CapacidadRespiratoria (un estudio realizado por una compañía farmacéutica para examinar los efectos de tres drogas sobre la capacidad respiratoria de pacientes de asma [Fuente: Software InfoStat]), prepare un gráfico de barras de manera que pueda comparar cómo cambia con el tiempo la capacidad respiratoria promedio bajo los distintas drogas. “Hora” = número de horas después de administrar la droga [Ayuda: Querremos “hora” en el eje X (“criterios de clasificación”), y droga en “particiones” (para tener barras adyacentes). Luego de “aceptar” por 1era vez, seleccione la opción de “particiones en el mismo gráfico” y “medidas de confianza, ninguna”, seguido por “aceptar” de nuevo). Laboratorio 3 – rev. 2014 - LWB Laboratorio 3: Resumen gráfico de la información II 1. Utilizando los datos de prueba Atriplex, prepare el siguiente gráfico de barras que presenta el porcentaje de germinación en semilla de diferentes tamaños, con color de episperma en barras adyacentes. (ayuda: utilice las opciones de “medidas de confianza, ninguna” y “particiones en el mismo gráfico”) % Germinación 100 75 50 25 0 chicas medianas grandes Tamaño de Semilla episperma claro epispera oscuro episperma rojizo 2. Usando los datos de Atriplex, prepare un gráfico de puntos para graficar PS (peso de semillas) en el eje vertical y color (episperma) en el eje horizontal. ¿Deberían usarse conectores para unir las medias de PS en cada color? 3. Usando los datos de café, construya una tabla de frecuencias para la variable altura (en metros) usando InfoStat (menú Estadísticas>Tablas de Frecuencias). Escoja “número de clases personalizado”, con valor mínimo de .905, máximo de 5.105 y 7 clases (verificar que esto les da un ancho de clase de 0.6, como deseamos). Ahora prepare un histograma de frecuencias absolutas a mano (usando la tabla de frecuencias como base) y en Infostat (menú Gráficos>Histograma, use las mismas clases que usó para la tabla de frecuencias: comience con 0.905m (como extremo inferior de la primera clase) y use un ancho de clase de 0.6 m. Tanto para tablas de frecuencias como para histogramas, en InfoStat se puede indicar qué tipo de tabla/gráfica se desea (con límites de clase o marca de clase en el eje X; frecuencia absoluta, frecuencia relativa, frecuencia absoluta acumulada o frecuencia relativa acumulada en el eje Y). Practica el cálculo a mano de valores como límites de clase, marca de clase, frecuencias absolutas, etc. 4. Usando los datos del archivo salinidad, construya un histograma y una ojiva para biomasa. Use la ojiva para contestar las siguientes preguntas: (a) ¿Qué porcentaje de las observaciones tienen biomasa menor de 1000? Laboratorio 3 – rev. 2014 - LWB (b) ¿Qué porcentaje de las observaciones tienen biomasa mayor de 2000? (c) 60% de las observaciones tienen biomasa menor de ________. (d) 35% de las observaciones tienen biomasa mayor de ___________. 5. Use los datos de ajo blanco. Construya un histograma de frecuencias relativas y un polígono de frecuencias acumuladas para la variable perímetro. Aproximadamente, ¿qué porcentaje de las observaciones tienen perímetros mayores de 20? 6. En las gráficas en la próxima página, indique el nombre de cada gráfica, mencione cuáles gráficas están correctas y cuáles podrían inducir a interpretaciones erróneas o falaces. Justifique brevemente. Laboratorio 4 – rev. 2014 - LWB Laboratorio 4: Estadísticos descriptivos 1. Calcule los estadísticos indicados utilizando los datos de café. Realice los cálculos usando Infostat (“Medidas Resumen”) y su calculadora. Utilice las reglas de redondeo discutidas en la última página de este laboratorio. En InfoStat (“Estadísticas/Medidas Resumen”): Var(n-1) = varianza muestral (s2) Var(n) = varianza poblacional (2) D.E. = desviación estándar muestral Suma = Y Suma Cuad. = Y2 SCC* = “suma de cuadrados corregida” (fórmula teórica: (Y- 𝑌)2; fórmula de trabajo: Y2 – [(Y)2/n]) *en anova, InfoStat usa las siglas “SC” S.C./(n-1) = varianza Esta parte de la ecuación de la S.C. (=SCC) se llama el “factor de corrección” a) Diámetro (en cm) de árboles enfermos (ayuda: ordenar los datos por “enfermo”, seleccionar las filas con enfermo = no, y desactivar los casos seleccionados con click derecho, “desactivar caso”; luego se puede activar los casos de nuevo) n Yi ______ i 1 s 2 _____ Md _____ n Y i 1 2 i _____ s _____ Q1 _____ Y _____ n _____ C.V . _____ Q3 _____ IQR=_____ b) Altura (en m) de árboles (todos juntos): n Yi ______ i 1 s 2 _____ Md _____ n Y i 1 i 2 _____ s _____ Q1 _____ Y _____ n _____ C.V . _____ Q3 _____ IQR=_____ 2. Utilizando la media y desviación estándar muestral calculados en la parte 1.b, determine el porcentaje de árboles de café cuyas alturas están dentro de los intervalos en la tabla en la próxima página. ¿Están de acuerdo estos porcentajes con aquellos que se esperarían de acuerdo a la regla empírica? Justifique su respuesta. Laboratorio 4 – rev. 2014 - LWB Intervalo Límite Inferior del intervalo Límite Superior del intervalo Número de observaciones en el intervalo Porcentaje de observaciones en el intervalo Porcentaje de observaciones en el intervalo de acuerdo con la regla empírica 𝑌- s 𝑌 – 2s 𝑌 – 3s 3. La edad media de 5 personas en una habitación es de 20 años. Una persona de 26 años entra a la habitación. ¿Cuál es ahora la edad media de las 6 personas? 4. Considere los datos de prueba Hembras. Nos interesa estudiar si la longitud de la cola de nemátodos (lcola) depende de la temperatura ambiental. ¿Qué estadístico descriptivo (medida resumen) le permite estudiar esta relación? Utilizando InfoStat, prepare una tabla con este estadístico descriptivo para cada temperatura. Indique sus conclusiones. 5. El siguiente gráfico representa los datos de biomasa estudiados en el laboratorio 3. Usando esta gráfica indique los valores aproximados de la mediana, los cuartiles y el recorrido intercuartílico y apunte sus contestaciones en la tabla en la próxima página. Calcule los mismos estadísticos usando Infostat y compare los resultados. Polígono de frecuencias acumuladas 1.00 0.95 0.90 0.85 0.80 frec. rel. acumulada 0.75 0.70 0.65 0.60 0.55 0.50 0.45 0.40 0.35 0.30 0.25 0.20 0.15 0.10 0.05 0.00 200 400 300 600 500 800 700 1000 1200 1400 1600 1800 2000 2200 2400 900 1100 1300 1500 1700 1900 2100 2300 2500 Biomasa Laboratorio 4 – rev. 2014 - LWB Valores aproximados usando la ojiva arriba Valores calculados en InfoStat Mediana (=Q2) Q1 Q3 Recorrido Intercuartílico (IQR) 6. Usando los datos del archivo CapacidadRespiratoria, realice un gráfico de caja que le permita comparar las capacidades respiratorias bases de los pacientes sometidos a las tres drogas diferentes. Un supuesto del experimento es que los pacientes asignados a los tres tratamientos diferentes iniciaron el experimento con capacidades respiratorias bases similares. ¿Existe evidencia de que se cumplió con este supuesto? Entre drogas, ¿Cómo comparan las distribuciones de las capacidades respiratorias bases? ¿Son parecidas o diferentes? 7. Usando los datos de café, realice gráficos de caja para altura de árboles enfermos y no enfermos. Conteste las siguientes preguntas: a. Entre los árboles enfermos, el 50% de los árboles miden menos de __________ metros. b. Entre los árboles no enfermos, el 50% de los árboles miden menos de __________metros. c. Entre los árboles enfermos, el 75% de los árboles miden más de ___________metros. d. Entre los árboles no enfermos, el 25% de los árboles más bajos miden menos de ___________metros. e. Los árboles enfermos que tienen alturas entre Q1 y Q3 representan _______% de la distribución y sus valores están entre ______ metros y _______ metros f. La media de altura para árboles no enfermos es aproximadamente _________metros. g. La mediana de altura para árboles no enfermos es aproximadamente _________metros. h. ¿Cuál muestra de árboles tiene mayor variabilidad? ¿Por qué? Comente sobre la simetría de las dos distribuciones. (¿Cuál es más simétrica y porque?) (Reglas de redondeo – próxima página) Laboratorio 4 – rev. 2014 - LWB REGLAS DE REDONDEO 1. Utilice un dígito decimal adicional a la cantidad de decimales presentados en las observaciones originales. 2. Redondee su respuesta final, y no los cálculos intermedios (por ejemplo, no use una varianza redondeada para calcular la desviación estándar). 3. Cuando un 5 (exactamente un 5) tiene que ser redondeado: redondee hacia arriba cuando el dígito previo es impar, y redondee hacia abajo si el dígito previo es par. Ejemplo 1. Los datos originales son enteros (se redondea a un lugar decimal). ¿Cómo se redondean los siguientes valores calculados? 58.4780, 58.4500, 58.4219, 58.3750, y 58.3500 ----------------- 58.5 58.4780 = 58.5 (valor calculado está más cercano a 58.5 que a 58.4) 58.4500 = 58.4 (valor calculado es exactamente un 5 en medio de 58.4 y 58.5) Dígito previo es par; se redondea hacia abajo 58.4219 = 58.4 (valor calculado está más cercano a 58.4 que a 58.5) 58.4 58.3750 = 58.4 (valor calculado está más cercano a 58.4 que a 58.3) 58.3500 = 58.4 (valor calculado es exactamente un 5 en medio de 58.3 y 58.4) Dígito previo es impar; se redondea hacia arriba 58.3 Ejemplo 2 (datos originales son enteros). Valor calculado Valor redondeado 58.4500 58.4 58.3500 58.4 58.4506 58.5 58.3512 58.4 58.4219 58.4 58.4780 58.5 58.9981 59.0 58.0136 58.0 Ejemplo 3 (datos originales tienen un decimal) Valor calculado Valor redondeado 1.5650 1.56 1.5550 1.56 1.2135 1.21 1.3765 1.38 1.7051 1.71 1.9921 1.99 1.9962 2.00 1.0028 1.00 Laboratorio 5 – rev. 2014 - LWB Laboratorio 5: Probabilidad y Distribución Binomial 1. Para el experimento aleatorio de arrojar 3 monedas diferentes (una de $0.05, una de $0.10 y una de $0.25), realice una lista con los 8 resultados igualmente probables. (cara = C ; cruz = X). Resultado $0.05 1 C 2 3 4 5 6 7 8 $0.10 C $0.25 C Espacio de trabajo a. Calcule P(A=observar menos de 2 caras). (ayuda: en el espacio de trabajo arriba, entre “A” para cada resultado que cumple con “menos de 2 caras”; por ejemplo, el primer resultado no cumple) b. Calcule P(B=observar 1 o más caras). c. Calcule P(C=exactamente 3 caras). d. ¿Son A y B mutuamente excluyentes? e. ¿Son A y C mutuamente excluyentes? f. ¿Son B y C mutuamente excluyentes? g. Calcule P(A ∩ B) h. Calcule P(A ∪ C) i. Calcule P(C̅) 2. Considere nuevamente el experimento de arrojar tres monedas diferentes, y defina la variable aleatoria Y = cantidad de caras que se obtienen. a. ¿Es ésta una variable aleatoria discreta o continua? 15 Laboratorio 5 – rev. 2014 - LWB b. Realice una lista de los posibles valores de Y, y calcule las probabilidades de cada uno de ellos. Y P(Y) 0 1 2 3 c. Usando InfoStat (gráfico de barras), grafique la distribución de probabilidad calculada en la parte (b). 3. La tabla siguiente representa los resultados de un estudio para comparar un tratamiento nuevo para prevenir el resfrío común. Trescientos pacientes fueron tratados, mientras que 200 pacientes comparables no se trataron. Los resultados indican la cantidad de pacientes que no tuvieron ningún resfrío, un resfrío o más de un resfrío durante la temporada invernal. Pacientes Tratados No tratados Total No 145 80 225 Resfríos Uno 80 70 150 Total Más de uno 75 50 125 300 200 500 a. Si un paciente se escoge al azar de entre los 500 pacientes del estudio, i. ¿cuál es la probabilidad de que haya sido tratado y no haya tenido resfríos? ii. ¿cuál es la probabilidad de que no haya sido tratado y haya tenido uno o más resfríos? b. Si un paciente se escoge al azar de entre los 300 pacientes tratados, i. ¿cuál es la probabilidad de que no haya tenido resfríos? ii. ¿cuál es la probabilidad de que haya tenido más de un resfrío? c. Si un paciente se escoge al azar de entre los 200 pacientes no tratados, i. ¿cuál es la probabilidad de que no haya tenido resfríos? ii. ¿cuál es la probabilidad de que haya tenido más de un resfrío? d. Comparando sus respuestas a las preguntas (c) y (e), ¿podría afirmar que el tratamiento parece efectivo? 16 Laboratorio 5 – rev. 2014 - LWB 4. En estudios ecológicos nos interesa estudiar cómo dos especies de árboles se mezclan o se separan en un bosque. Supongamos que estamos estudiando dos especies, A y B. Un método para medir su asociación es muestrear aleatoriamente un árbol, ver de qué especie es, y entonces observar la especie del árbol vecino más cercano. Este proceso se repite para muchos árboles. Se muestran los datos obtenidos para dos bosques. Árbol muestreado Bosque I A B Total A 30 10 40 B 5 55 60 Total 35 65 100 Bosque II Árbol muestreado Vecino más cercano Vecino más cercano A B Total A 5 35 40 B 30 30 60 Total 35 65 100 a. Para un árbol elegido al azar en el bosque I, encuentre la probabilidad que, i. Sea de la especie A. ii. Tenga un vecino de la especie A, dado que se observó que el árbol muestreado era de la especie A. iii. Tanto el árbol muestreado como su vecino sean de la especie A. iv. Tanto el árbol muestreado como su vecino sean de la misma especie. b. Responda las preguntas anteriores para un árbol elegido al azar en el bosque II. v. Sea de la especie A. vi. Tenga un vecino de la especie A, dado que se observó que el árbol muestreado era de la especie A. vii. Tanto el árbol muestreado como su vecino sean de la especie A. viii. Tanto el árbol muestreado como su vecino sean de la misma especie. 17 Laboratorio 5 – rev. 2014 - LWB c. ¿Cuál de los bosques parece tener mayor separación entre las especies (mayor separación entre especies)? ¿Por qué? Distribución binomial. Para calcular probabilidades de la distribución binomial (y otras) en Infostat se puede usar el menú Estadísticas > Probabilidades y cuantiles, seleccionando la opción de distribución binomial. Favor de redondear tus contestaciones a cuatro lugares decimales. La salida de InfoStat utiliza la fórmula binomial para calcular varias probabilidades, como ilustrado en el ejemplo abajo: Valor deprobablidad de éxito) Valor de y (# de éxitos en n ensayos) La probabilidad de que la variable aleatoria Y sea menor o igual (< = ) a y (el valor especificado). Por ejemplo, aquí 0.3633 es la probabilidad de que Y sea menor o igual a 3 (= P(3) + P(2) + P(1) + P(0)] La probabilidad de que la variable aleatoria Y sea mayor que y. Aquí 0.6367 es la probabilidad de que Y sea mayor que 3 [= P(4) + P(5) + P(6) + P(7) + P(8)] Probabilidad de que Y sea exactamente 3 1. Suponga que solamente el 30% de los estudiantes en una escuela se ejercitan lo suficiente. Si se obtiene una muestra aleatoria de 10 estudiantes de esa escuela, a. ¿cuál es la probabilidad que ninguno de los estudiantes en la muestra se ejerciten lo suficiente? b. ¿Cuál es la probabilidad que 3 o menos de los estudiantes en la muestra se ejerciten lo suficiente? 2. Los entomólogos están a menudo interesados en estudiar el efecto de atrayentes químicos (feromonas) sobre los insectos. Una técnica común es liberar varios insectos a una distancia igual de la feromona bajo estudio y de una sustancia sin efecto (control). Si la feromona tiene efecto, más insectos se dirigirán hacia ella en vez de dirigirse hacia el control. Si no hay ningún efecto, un insecto se dirigirá hacia una de las dos posibilidades 18 Laboratorio 5 – rev. 2014 - LWB con igual probabilidad (es decir, la probabilidad que el insecto se dirija hacia la feromona es 0.5). En un experimento 5 insectos se liberan. Calcule las siguientes probabilidades suponiendo que la feromona no tiene ningún efecto. a. P(los cinco insectos se dirijan hacia la feromona) b. P(exactamente cuatro insectos se dirijan hacia la feromona) c. P(al menos 1 insecto se dirija hacia la feromona) 3. Una profesora de biometría va a dar un quiz con 10 preguntas “cierto-falso”. Supongamos que un estudiante adivina cada respuesta independientemente (es decir, no tiene idea del tema, = 0.5). a. ¿Cuál es la probabilidad que el estudiante acierte las 10 preguntas? b. ¿Cuál es la probabilidad que el estudiante acierte al menos 8 preguntas? c. ¿Cuál es la probabilidad que el estudiante acierte no más de 6 preguntas? d. Si la profesora decide que aprobarán el quiz todos los estudiantes que contesten correctamente por lo menos 6 de las 10 preguntas, ¿qué porcentaje de los estudiantes que adivinan cada respuesta pasarán el quiz? 4. De estudios previos, se conoce que sólo el 35% de las semillas de una planta en peligro de extinción son capaces de germinar bajo condiciones de invernadero. Se sembrarán 20 semillas. a. ¿Cuál es la probabilidad que germinen al menos la mitad de ellas? b. ¿Cuál es la probabilidad que germinen 5 o menos semillas? c. Si observamos que ninguna de las semillas ha germinado, ¿es razonable pensar que esta muestra vino de una población donde el porcentaje de germinación es 35%? Explique. 19 Laboratorio 6 – rev. 2014 - LWB Laboratorio 6: Distribución Normal 1. La tabla 1 del texto presenta la probabilidad de que un valor aleatorio de Z = (Y-µ)/ sea menor que el valor tabulado z (área bajo la curva entre menos infinito y z). Use la tabla de z para determinar las probabilidades siguientes. Incluya un gráfico en cada caso, sombrando la probabilidad (área) que se busca. a. P(Z<-2)= b. P(Z>2.56)= c. P(Z<-1.23)= d. P(Z<2.25)= e. P(-1.63<Z<2.57)= f. P(-1.70<Z<-0.25)= g. P(1.42<Z<1.89)= 2. En InfoStat, se puede usar el menú Estadisticas>Probablidades y Cuantiles para calcular probabilidades en la distribución normal. Use InfoStat para determinar las probabilidades siguientes y compare sus resultados con el ejercicio 1. a. P(Z<-2)= b. P(Z>2.56)= c. P(-1.63<Z<2.57)= d. P(-1.70<Z<-0.25)= e. P(1.42<Z<1.89)= 3. Use la tabla de z para encontrar el valor de a tal que la probabilidad sea la especificada. Incluya un diagrama en cada caso. (ayuda: la dirección de la flecha indica el lado de la distribución de ser sombrada. Esta área sombrada corresponde a la probabilidad indicada) a. P(Z<a)=.84 b. P(Z>a)=.19 (ayuda: es la misma a de P(Z< a)=0.81) c. P(Z<a)=.23 d. P(Z>a)=.65 (ayuda: es la misma a de P(Z< a)=0.35) e. P(-a<Z<a)=.90 4. Use InfoStat para encontrar el valor de a tal que la probabilidad sea la especificada. Compare sus resultados con el ejercicio 3. a. P(Z<a)=.84 b. P(Z>a)=.19 c. P(-a<Z<a)=.90 5. Otra alternativa para buscar probabilidades en Infostat es usar el menú Aplicaciones > Didácticas > Gráficos de funciones de densidad continuas. Aquí no sólo obtenemos las probabilidades sino también las gráficas. Para superponer varias gráficas es posible usar la opción clonar (herramientas gráficas). Se obtendrá una copia (clon) de la serie gráfica original. Si seleccionamos esta nueva serie podemos cambiar sus parámetros y comparar ambas distribuciones. Grafique en un mismo gráfico las funciones correspondientes a los siguientes tres distribuciones normales: 10, 2 1 , 10, 2 3 , 9, 2 3 . 20 Laboratorio 6 – rev. 2014 - LWB 6. Usando la definición de cuartiles (valores de la variable que dejan un 25% o un 75% de la distribución a la izquierda), calcule los valores de Q1 y Q3 en la distribución normal estandarizada. ¿Cuál es el valor de RIC (recorrido intercuartílico)? Use la tabla e Infostat. Para encontrar probabilidades asociadas con una distribución normal general se debe transformar el valor de Y en Z usando la fórmula abajo, y luego usar la tabla de z. z y Ejemplo: P(Y<115) = P(Z < [115-100)/6] )= P(Z<2.50) = 0.9938. El problema inverso (encontrar un valor de Y que acumule cierta probabilidad) se resuelve calculando primero el valor de Z y después resolviendo la ecuación z y en la siguiente manera: y = z + Ejemplo: Dado Y ~ N(100, 36), Encontrar a tal que P(Y<a)=0.6591: A partir de las tablas de Z, vemos que P(Z<.41)=.6591. Entonces a = (.41)(6) + 100 = 102.46. 7. Para Y ~ N ( 100, 36) , calcule las siguientes probabilidades. Incluya un diagrama en cada caso. Use tablas e InfoStat. a. P(93<Y<102)= b. P(90<Y<95)= c. P(Y>103)= d. P(Y<98)= 2 8. Para la misma situación Y ~ N ( 100, 36) , calcular los valores de a. Incluya un diagrama en cada caso. Use tablas e InfoStat. a. P(Y>a)= .25 b. P(Y<a)= .08 c. P(Y>a)= .72 d. P(Y<a)= .995 2 21 Laboratorio 6 – rev. 2014 - LWB 9. Un programa de selección en maíz trata de obtener plantas no demasiado altas. Suponga que la altura de las plantas sigue una distribución normal con media 160 cm y desviación estándar 21 cm. a. ¿Qué proporción de las plantas van a ser eliminadas si se decide descartar todas las plantas cuya altura exceda 180 cm? (ayuda: P(Y>180) =?) b. ¿A partir de qué altura se deberían descartar las plantas si se desea eliminar el 20% del lote con las plantas más altas? (ayuda: P(Y>a) = 0.20) 10. La cantidad de oxígeno disuelta en el agua de ríos depende de la temperatura, la cantidad de materia orgánica en descomposición, de la presencia de contaminantes, etc. El Council of Environmental Quality (CEQ) considera que un contenido de oxígeno disuelto menor de 5 mg/l es indeseable porque no sería capaz de sustentar la vida acuática. Suponga que una planta industrial descarga sus residuos en el río y las mediciones de oxígeno disuelto corriente abajo de la descarga tienen una distribución normal con media de 6.5 mg/l y desviación estándar de 0.6 mg/l. a. ¿Qué proporción de los días será el contenido de oxígeno disuelto considerado indeseable por el CEQ? b. ¿Hasta qué valor podría caer el contenido de oxígeno disuelto? (ayuda: ¿entre qué valores de la variable Ud. espera encontrar virtualmente todas las observaciones?) 11. La longitud del caparazón del langostino Thenus orientalis, encontrado comúnmente en los mercados de Singapur, tiene una distribución aproximadamente normal, con una media de 59.5 mm y una desviación estándar de 4.6 mm. a. Si va a seleccionar aleatoriamente un langostino de esta población, ¿qué probabilidad tiene de que éste tenga una longitud menor de 55mm? b. Si el gobierno decretara que todos los langostinos que se vendan en el mercado deben tener una longitud mínima de 50mm, ¿qué proporción de los langostinos serán de un tamaño ilegal para la venta? c. Un comerciante tiene una anuncio que dice “Nosotros garantizamos que los todos los langostinos que vendemos en este negocio son los más grandes disponibles”. ¿Qué longitud mínima deberían tener para asegurarnos que esto langostinos están en el 10% superior de la población? 22 Laboratorio 7 – rev. 2014-LWB Laboratorio 7: Distribuciones Muestrales La siguiente es la distribución de una población (artificial) con 10 individuos (elementos). A la derecha tenemos los valores de cada elemento (supongamos, p.ej., que son diámetros de árboles). Los parámetros de esta población son 2.5, 2 1.45. Población original frecuencia absoluta 4 3 2 1 0 1 1 2 3 4 5 6 Columna4 1. Generar en Infostat todas las muestras posibles de tamaño n=2 y n=5 (se puede usar el menú Aplicaciones>Didácticas>Todas las muestras posibles). Calcular la media de cada muestra y guardar estas medias en dos columnas de datos (usar copiar/pegar). Graficar la distribución muestral de la media para ambos tamaños usando la misma escala horizontal (0 a 0.70). a. ¿Cuál de las dos distribuciones tiene menos variabilidad? b. ¿Cómo se comparan las medias de ambas distribuciones? c. ¿Son suficientemente grandes los tamaños de estas muestras como para que las distribuciones parezcan normales? 2. El archivo zanahoria.idb contiene los pesos de 144 zanahorias (en g). a. Calcule la media y la varianza de la población. b. Prepare un histograma de frecuencias relativas con las observaciones en esta población (use para el eje horizontal un valor mínimo de 0 y un máximo de 1200). 3. Para verificar las propiedades de la distribución muestral de la media, vamos a tomar muestras con reemplazo (“aleatorio con reposición”) de la población de zanahorias descripta en la parte2. Use el menú Aplicaciones>Didácticas>Muestreo-Remuestreo. 23 Laboratorio 7 – rev. 2014-LWB a. Escoja 1000 muestras con reposición de tamaño n=4 y use la opción de guardar la media muestral. b. Calcule la media y la varianza poblacionales de la población de 1000 medias de tamaño n=4. c. Prepare un histograma de frecuencias relativas de la población de 1000 medias de tamaño 4. (Use para el eje horizontal un valor mínimo de 0 y un máximo de 1200 con 9 ticks y para el eje vertical 0 a 0.35 con 8 ticks.) d. Repita las partes a, b y c para tamaño de muestra n=16. e. Comparar las medidas de resumen de la población original, de la población de medias de n=4, y de la población de medias de n=16. f. Comparar los histogramas de la población original, de la población de medias de n=4, y de la población de medias de n=16. 4. La distribución del porcentaje de grasa láctea en ganado Holstein durante la década de 1970 era aproximadamente normal con una media de 3.4 y una desviación estándar de 0.3. (a) ¿Qué porcentaje de las vacas producían leche con menos de 3 de grasa? (b) ¿Qué porcentaje de las vacas producían leche con más de 4 de grasa? (c) Calcule el percentil 95 de la distribución de grasa láctea. Interprete este valor. 5. Supongamos que una muestra aleatoria de n 25 vacas Holstein se selecciona de la población mencionada en el problema 4. A cada vaca se le mide el porcentaje de grasa en su leche, y se calcula la media muestral. (a) ¿Cómo sería la distribución de los valores posibles de Y ? (b) Compare la forma de la distribución de Y con la forma de la distribución de Y (el porcentaje de grasa láctea en cada vaca). (c) Calcule la probabilidad que una muestra aleatoria de tamaño 25 tenga una media muestral menor de 3. Compare este resultado con el de 4a. 24 Laboratorio 8 Laboratorio 8: Intervalos de Confianza y Pruebas de Hipótesis 1. Usando Infostat, genere 100 intervalos de confianza del 90% y calcule el porcentaje que no cubren a la media verdadera (use el menú Aplicaciones>Didácticas>Intervalos de confianza). Realice esto para datos de una distribución normal con 20, 2 9 y tamaños de muestra n=5, n=20, n=50. a. ¿Cambian significativamente los porcentajes de cobertura según cambia el tamaño muestral? b. ¿Cómo se comparan los anchos de estos intervalos? Grafíquelos en la misma escala. 2. Determine el tamaño de muestra si se sabe que 2=100 y que los L.C. del 95% son 17.2 y 22.8. Realícelo a mano y usando Infostat (Estadísticas>Cálculo de tamaño muestral>Para estimar una media con una precisión dada). 3. Un biólogo desea estimar el efecto de un antibiótico sobre el crecimiento de una bacteria. Experiencias anteriores indican que la desviación estándar del crecimiento (medido en cm2) en placas de Petri con antibiótico añadido es 13 cm2. Determine el número de placas que tiene que preparar para estimar el crecimiento promedio con un error de no más de 3 cm2 (esto es, se desea que la media poblacional de crecimiento no esté a una distancia mayor que 3 de la media muestral). Use un nivel de confianza del 99%. Verifique sus resultados con Infostat. 4. Se desea llevar a cabo un estudio sobre el peso promedio de chillos de tamaño comercial en el área de La Parguera. Estudios previos realizados hace varios años indican que la varianza del peso de chillos es de 1.6 lb2.Determine el tamaño de muestra que se requeriría si se va a estimar el peso promedio con un error de 0.5 lb (y una confianza del 95%). Verifique sus resultados con Infostat. 5. Para la situación anterior, ¿cómo se podría aproximar la varianza si no se tuviera información previa? 6. Se desea probar que, luego de un tratamiento para un problema cardíaco, los pacientes pueden ejercitarse más de 2 minutos. Se registró el incremento en la capacidad de realizar ejercicios (en minutos) para 90 pacientes adultos. La media muestral fue de 2.2 minutos, y la desviación estándar de 1.05. Use estos datos para probar la hipótesis nula H0: =2 versus Ha: >2. Use =.05 e indique sus conclusiones en términos de este problema. 7. Calcule el nivel de significancia observado de la prueba realizada en la parte 6 (“valor p”) y úselo en vez de la región de rechazo para probar las hipótesis. Presente un gráfico en Infostat (Aplicaciones >Didácticas> Gráfico de funciones de densidad continuas) 8. Se sospecha que las vacas en Puerto Rico están más infestadas por garrapatas (Boophilus microplus) que en el resto del Caribe (donde la infestación promedio es 130 25 Laboratorio 8 garrapatas/vaca). Una muestra aleatoria de 80 vacas en Puerto Rico presentó un promedio de 134.1 garrapatas por vaca, con una varianza de 50. Calcule el intervalo de confianza del 90% para , el promedio de garrapatas por vaca en Puerto Rico. b. Formule y pruebe las hipótesis de interés (=.05). a. 26 Laboratorio 9 Laboratorio 9: Pruebas t para una y dos muestras independientes Pruebas de hipótesis para una media usando la distribución t. Ejemplo resuelto en Infostat Se ha realizado un estudio para determinar si cerdos alimentados con una dieta reformulada aumentan más de 20 lbs (en promedio) durante un periodo de alimentación de un mes. Para ello se usaron 12 cerdos, cuyos aumentos de peso se presentan a continuación: 17, 22, 20, 19, 53, 21, 25, 40, 30, 19, 11, 16 Hipótesis H0 : 20 Ha : 20 Región de rechazo: Y 0 24.417 20 1.313 s 11.650 n 12 t t0.05,11gl 1.796 Conclusiones: No se rechaza H0 . Estadístico de la prueba: t 27 Laboratorio 9 1. Calcule las siguientes probabilidades usando la tabla t e InfoStat. Incluya un diagrama en cada caso. a. P(T>1.356) si gl=12 b. P(T<2.101) si gl=18 c. P(T<-1.319) si gl=23 d. P(T<-1.711) si gl=24 e. P(T<.697) si gl=11 2. Determine los valores críticos (valores en la tabla) de t, haga un diagrama de la distribución y lleve a cabo las pruebas indicadas. Calcule los valores p usando el calculador de probabilidad de Infostat (o el graficador). a. H0 : 30, Ha : 30, n 16, Y 32, s2 25, 0.05 b. H0 : 58, Ha : 58, n 18, Y 57, s2 100, 0.05 c. H0 : 25, Ha : 25, n 25, Y 9, s2 20, 0.05 d. H0 : 430, Ha : 430, n 10, Y 400, s2 14, 0.01 3. Los rendimientos de 7 plantas de piña aleatoriamente escogidas, variedad “Cabezona”, fueron 4.2, 5.6, 4.3, 4.8, 5.7, 5.5 y 4.9 kg/planta. (a) Construya un intervalo de confianza del 95% para la media poblacional. (b) Pruebe H0: =4.5, Ha: 4.5 usando =.05. (c) Repita los pasos 1 y 2 usando InfoStat. 4. Se condujo un experimento para examinar la susceptibilidad de raíces de cierta variedad de limonero a una larva específica con el objetivo de probar si la cantidad de larvas en las raíces era menor en esta variedad que lo que normalmente se encuentran en las variedades tradicionales. 28 Laboratorio 9 Cuarenta y un plantas se expusieron a la larva, y se examinaron luego de cierto tiempo. La respuesta de interés es el logaritmo del número de larvas por gramo encontradas en cada raíz. Para las 41 plantas estudiadas, la media muestral fue 9.02 y la desviación estándar 1.12. (a) Pruebe la hipótesis que =10 versus <10 usando =.01. (b) Calcule el valor p usando InfoStat. (c) Construya un intervalo de confianza del 95% para la susceptibilidad media de las raíces. 5. En una compañía farmacéutica se desea comparar la presión arterial sistólica de empleadas que usan anticonceptivos orales que no usan anticonceptivos orales (todas entre 30 y 35 años de edad). Se obtuvieron dos muestras aleatorias: una de 8 empleadas que usan anticonceptivos orales y otra de 21 empleadas que no usan anticonceptivos orales, y se les midió la presión arterial (mm Hg). Los resultados fueron los siguientes: Usan anticonceptivos orales: n=8, Y = 132.8 mm Hg, s=15.3 mm Hg No usan anticonceptivos orales: n=21, Y = 127.4 mm Hg, s=18.2 mm Hg (a) Conduzca una prueba para determinar si hay diferencias significativas entre las medias. Use =.05. (b) Pruebe si las empleadas que usan anticonceptivos orales tienen una presión arterial sistólica mayor (en promedio) que las no los usan. Use =.05. 6. Un inspector de control de contaminación sospechaba que una comunidad ribereña estaba descargando aguas servidas no-tratadas en el río y eso cambiaba el nivel de oxígeno disuelto en el río. Para probar esto, obtuvo 5 muestras aleatorias de agua del río en una zona río arriba del pueblo, y otras 5 muestras en una zona río abajo del pueblo. Se midieron los niveles de oxígeno disuelto, en ppm. ¿Proveen los datos evidencia de un contenido menor de oxígeno río abajo? Use =.05. Río arriba: 4.8, 5.2, 5.0, 4.9, 5.1 Río abajo: 5.0, 4.7, 4.9, 4.8, 4.9 7. Un estudio se realizó en 16 vacas lecheras. Ocho vacas fueron asignadas aleatoriamente a un régimen de líquidos de agua solamente (grupo 1), y las otras recibieron suero líquido solamente (grupo 2). Además, a cada animal se le dio 7.5 kg de grano por día, y se le permitió comer heno a voluntad. Se registró, entre otras cosas, la cantidad de heno (en kg/vaca) consumido diariamente. Grupo 1: 15.1, 14.9, 14.8, 14.2, 13.1, 12.8, 15.5, 15.9 Grupo 2: 6.8, 7.5, 8.6, 8.4, 8.9, 8.1, 9.2, 9.5 (a) Pruebe la hipótesis que hay diferencias entre los consumos diarios promedios de heno en los dos grupos con =.01. (b) Construya un intervalo de confianza del 99% para la verdadera diferencia entre la medias de ambos grupos. El intervalo obtenido, ¿contiene el valor 0? ¿Qué relación tiene esto con sus conclusiones en la parte a? (c) ¿Cuáles son los supuestos necesarios para las pruebas realizadas en la parte a? Comente sobre su validez en este caso (grafique los datos si fuese necesario). 29 Laboratorio 10 Laboratorio 10: Pruebas t para muestras pareadas PARTE I. Incluya en cada caso todos los pasos necesarios para probar las hipótesis correspondientes, una gráfica con ttab, cálculo del valor p, conclusiones e interpretaciones. A menos que esté especificado de otra manera, use =.05. 1. Se desean comparar los rendimientos de dos nuevas variedades de maíz. Debido a que existe una gran variabilidad en los rendimientos en distintas fincas, se escogieron 7 fincas al azar, y se plantó una parcela con cada una de las variedades en cada finca. Los resultados del experimento son los siguientes (en ton/ha): Finca 1 2 3 4 5 6 7 Variedad A 4.82 4.46 4.97 4.05 5.46 4.71 5.14 Variedad B 4.15 4.01 4.40 4.12 4.98 4.17 4.68 (a) Pruebe la hipótesis de igualdad en los rendimientos de las dos variedades versus la alternativa a dos colas. Use =.05. (b) Construya un intervalo de confianza del 95% para 1-2, la verdadera diferencia entre los rendimientos de las variedades A y B. . El intervalo obtenido, ¿contiene el valor 0? ¿Qué relación tiene esto con sus conclusiones en la parte a? 2. Los datos siguientes son logaritmos de recuentos de bacterias en siete botellas de leche (escogidas aleatoriamente), tomados antes y después de un tratamiento térmico. Se desea conocer si el tratamiento reduce el número de bacterias. Formule y pruebe las hipótesis de interés usando =.05. Botella 1 2 3 4 5 6 7 Antes Después 6.98 6.95 7.08 6.94 8.34 7.17 5.30 5.15 6.26 6.28 6.77 6.81 5.45 5.36 3. Se tomaron 11 hojas, una de cada una de 11 plantas de tabaco. Cada hoja se dividió en dos mitades. Una de las mitades se eligió al azar y se trató con preparación I y la otra mitad se trató con preparación II. El objetivo del experimento era comparar los efectos de las dos preparaciones del virus del mosaico sobre el número de lesiones después de un cierto período de tiempo. Los datos se presentan en la siguiente tabla: 30 Laboratorio 10 Planta Prep. I 1 18 2 20 3 9 4 14 5 38 6 26 7 15 8 10 9 25 10 7 11 13 Prep. II 14 15 6 12 32 30 9 2 18 3 6 PARTE II: Trabajando en grupos de 2-3 estudiantes, decida cuál de las pruebas t (para muestras independientes o para datos pareados) usaría Ud. en cada una de las siguientes situaciones. Presente las hipótesis nula y alternativa. Justifique brevemente. 4. Una corporación petrolera está interesada en realizar algunas pruebas preliminares para comparar una nueva mezcla de gasolina con otra actualmente en el mercado. Diez automóviles idénticos se asignaron aleatoriamente, 5 a una gasolina y 5 a la otra gasolina. Cada automóvil se llenó con 10 galones de gasolina y se condujo en una pista de pruebas hasta que la gasolina se agotó. El resultado fueron las millas recorridas en cada caso. 5. Una compañía tiene una política muy generosa (pero muy complicada) para ofrecer el bono de navidad al personal gerencial de menor rango. El factor clave en la decisión es un juicio subjetivo de la "contribución a los objetivos de la corporación". Un encargado de personal tomó muestras de 20 gerentes mujeres y 20 gerentes hombres para ver si había diferencias entre los bonos. Las observaciones se registraron como un porcentaje del salario anual. 6. En un estudio de los posibles factores que influyen en la frecuencia de pájaros embestidos por aviones (que, irónicamente, se ve como un peligro para los aviones), el nivel de ruido de varios aviones se midió dos segundos después del despegue (momento en que las ruedas dejan de tocar tierra). Veintidós jets de cabina ancha y 10 jets de cabina angosta se midieron y sus niveles de ruido se compararon. 7. Dos aleaciones se usan en la fabricación de barras de acero. Se desea comparar la resistencia de las barras hechas con cada aleación. Se toman muestras aleatorias de 9 barras de la aleación A y de 15 barras de la aleación B. 8. Con el objeto de estudiar el crecimiento de bacterias bajo dos dosis distintas de un cierto bactericida, se prepararon 20 placas de Petri. En 10 de ellas se colocaron 200 ppm del bactericida en el medio de cultivo, y en las otras 10, 1000 ppm. Luego de inocular las placas con las bacterias, se colocaron en una cámara en forma completamente aleatoria, y al cabo de cierto tiempo se midió el crecimiento radial de las bacterias. 9. Para estudiar el efecto de la exposición de flores de alfalfa a diferentes condiciones ambientales se escogieron 10 plantas vigorosas con flores expuestas libremente en la parte 31 Laboratorio 10 alta, y flores escondidas en la parte basal. Se determinó el número de semillas producidas por 10 vainas en cada ubicación (parte superior y parte inferior). 10. Con el objeto de evaluar si una nueva formulación permite obtener mayores aumentos de peso, una muestra de 8 novillos es alimentada con la ración regular, y otra muestra de 8 novillos es alimentada con la ración reformulada. Se analizan los pesos de los novillos luego de un año. 11. Para estudiar el efecto de un tratamiento con fungicidas (usado para eliminar hongos) a plantas de geranio, se registró la densidad de esporas del hongo Phytium sp. antes de aplicar un tratamiento a 15 tiestos con plantas de geranio. A los 10 días de aplicar el tratamiento, los mismos tiestos se evaluaron nuevamente y se registró la densidad de esporas del mismo hongo. 32 Laboratorio 11 Laboratorio 11: Análisis de la Varianza 1. Se está diseñando un experimento para comparar 4 variedades de habichuela. Se usarán 6 parcelas con cada una de las variedades en un diseño completamente aleatorizado en un área experimental homogénea rectangular de 8x3 parcelas. a. Prepare un mapa del área experimental con la asignación de los distintos tratamientos (=variedades) a cada una de las parcelas. b. Prepare un esquema de la tabla de ANOVA indicando fuentes de variación y grados de libertad. 2. Se condujo un experimento para comparar el contenido de almidón en plantas de tomate bajo distintos nutrientes (control, A o B). Doce plántulas se seleccionaron para el estudio, asignándose cuatro a cada uno de los tratamientos aleatoriamente. Cada planta se colocó en un tiesto con el nutriente correspondiente, y se ubicaron al azar en un invernadero. El contenido de almidón en los tallos se determinó 25 días después (en g/mg). Control Nutriente A Nutriente B 21 12 7 18 14 9 16 15 6 14 10 7 a. Formule y pruebe las hipótesis de interés usando =.05 (use InfoStat y verifique sus resultados con las fórmulas de trabajo presentadas en la conferencia). b. Realice todas las comparaciones de a pares usando el método de DMS de Fisher. Use =.05 (use InfoStat y verifique sus resultados con las fórmulas de trabajo presentadas en la conferencia). c. Construya un intervalo de confianza del 95% para la diferencia entre las medias del nutriente A y el control. d. Construya un intervalo de confianza del 99% para la media del nutriente B. 3. Se condujo un experimento para probar los efectos de 5 dietas diferentes en pavos. Seis pavos se asignaron aleatoriamente a cada uno de los 5 dietas, y se alimentaron por un período fijo de tiempo. Los resultados (libras de aumento de peso) se presentan a continuación. Use Infostat para resolver este ejercicio. Grupo Control Control+Dosis 1 del aditivo A Control+Dosis 2 del aditivo A Control+Dosis 1 del aditivo B Control+Dosis 2 del aditivo B Aumento de peso (lbs) 4.1, 3.3, 3.1, 4.2, 3.6, 4.4 5.2, 4.8, 4.5, 6.8, 5.5, 6.2 6.3, 6.5, 7.2, 7.4, 7.8, 6.7 6.5, 6.8, 7.3, 7.5, 6.9, 7.0 9.5, 9.6, 9.2, 9.1, 9.8, 9.1 33 Laboratorio 11 a. Pruebe las hipótesis de interés usando =.05. b. Realice todas las comparaciones de a pares (Prueba DMS de Fisher). c. Grafique sus resultados. Incluya líneas (“bigotes”) sobre las barras que representen el valor del DMS. d. Construya un intervalo de confianza del 90% para la media del grupo control. 4. Se probaron 5 métodos para empacar y congelar yuca. De un grupo de 25 yucas homogéneas se escogieron 5 aleatoriamente y se procesaron con el método I. Otras 5 se procesaron con el método II, y así sucesivamente. La respuesta de interés es el rendimiento (en % del peso inicial obtenidos luego del proceso) obtenido al final del proceso. Método I II III IV V Rendimientos 60, 52, 56, 52, 65 64, 74, 66, 64, 67 55, 66, 68, 57, 55 55, 56, 70, 59, 62 71, 65, 60, 69, 62 a. ¿Existen diferencias significativas entre los rendimientos promedio de los diferentes métodos? Pruebe usando =.05. b. Realice una prueba de DMS e indique claramente sus conclusiones. c. Grafique sus resultados. Incluya líneas (“bigotes”) sobre las barras que representen el valor del DMS. 5. Se desea saber si existen diferencias entre tres grupos de pacientes asmáticos en cuanto a su reacción al SO2 (cm H2O/s). Los grupos se definieron por su función pulmonar: grupo A, FEV1/FVS<75%; grupo B, FEV1/FVS entre 75% y 85%; grupo C, FEV1/FVS>85%. Grupo A B Reacción bronquial al SO2 20.8, 4.1, 30.0, 24.7, 13.8 7.5, 7.5, 11.9, 4.5, 3.1, 8.0, 4.7, 28.1, 10.3, 10.0, 5.1, 2.2 9.2, 2.0, 2.5, 6.1, 7.5 C a. ¿Existen diferencias significativas entre las reacciones al SO2 en los diferentes grupos? Pruebe usando =.05. b. Realice una prueba de DMS e indique claramente sus conclusiones. c. Grafique sus resultados. Incluya líneas (“bigotes”) sobre las barras que representen el valor del DMS. 34 Laboratorio 12 Laboratorio 12: Tablas de Contingencia 1. Los siguientes datos provienen de un experimento para estudiar el efecto del tratamiento de frío a plantas de azalea. Se escogieron plantas al azar de azalea, y se mantuvieron durante 30 días con el tratamiento correspondiente (frío / no frío). Luego de tratadas se contaron las yemas abiertas y cerradas en cada grupo de plantas. Los datos se presentan a continuación. Tratamiento Frío No Frío Yemas abiertas 143 116 Yemas cerradas 129 214 a. Calcule las frecuencias esperadas en cada celda bajo el supuesto que la proporción de yemas abiertas es la misma en ambos tratamientos (esto es, si la proporción de yemas abiertas es independiente del tratamiento). b. Calcule el estadístico 2 para probar la hipótesis de independencia. Indique sus conclusiones usando =.05. c. Grafique estos datos para apoyar sus conclusiones. 2. Los siguientes datos provienen de un estudio para comparar la opinión de agricultores respecto a una nueva política de importación de vegetales frescos. Se entrevistaron 230 agricultores y se clasificaron de acuerdo al tamaño de la finca (grande, mediana, pequeña) y a la opinión (1, completamente de acuerdo; 2, parcialmente de acuerdo; 3, parcialmente en desacuerdo y 4, completamente en desacuerdo). Tamaño | Chico Mediano Grande Opinión 1 1 1 2 2 19 10 5 3 30 25 33 4 50 44 10 a. Calcule el estadístico 2 para probar la hipótesis de independencia entre el tamaño de la finca y la opinión respecto a la nueva política. Indique sus conclusiones usando =.05. b. Grafique estos datos para apoyar sus conclusiones. 35 Laboratorio 12 3. La siguiente tabla proviene de un estudio de factores que afectan la elección de alimento en caimanes. Se usan datos de 219 caimanes capturados en cuatro lagos de Florida. La variable de respuesta es el tipo de alimento primario (en volumen) encontrado en el estómago del caimán. Esta respuesta tiene cinco categorías: (1) peces, (2) invertebrados, (3) reptiles, (4) aves y (5) otros. La categoría “otros” incluye anfibios, mamíferos, material vegetal, piedras, o la no existencia de un tipo dominante de alimento. Tamaño Hasta 2.3m Más de 2.3 m Total 1 49 45 94 2 45 16 61 Alimento 3 6 13 19 4 5 8 13 5 19 13 32 Total 124 95 219 a. El tipo de alimento dominante encontrado en el estómago, ¿depende del tamaño del animal? Formule y pruebe la hipótesis correspondiente usando =.01. b. Grafique sus datos e indique sus conclusiones. Interprete claramente sus conclusiones en términos de las categorías de alimento encontradas en cada tamaño de animal. 4. La tabla siguiente representa los resultados de un estudio para comparar un tratamiento nuevo para prevenir el resfrío común. Trescientos pacientes fueron tratados, mientras que 200 pacientes comparables no se trataron. Los resultados indican la cantidad de pacientes que no tuvieron ningún resfrío, un resfrío o más de un resfrío durante la temporada invernal. Pacientes Tratados No tratados No 145 80 Resfríos Uno 80 70 Total Más de uno 75 50 300 200 a. Calcule el estadístico 2 para probar la hipótesis de que la cantidad de resfríos no depende del tratamiento. Indique sus conclusiones usando =.05. b. Grafique estos datos para apoyar sus conclusiones. 36 Laboratorio 13 Laboratorio 13: Regresión y correlación lineal 1. Se condujo un experimento para examinar el efecto de diferentes concentraciones de pectina sobre la firmeza de batata enlatada. Se usaron tres concentraciones (0%, 1.5% y 3% de pectina). Se prepararon 6 latas con batatas en una solución de 25% de azúcar. Dos latas se asignaron aleatoriamente a cada una de las concentraciones de pectina, agregándose la concentración correspondiente de pectina antes de enlatar. Las latas se sellaron y almacenaron a 25C durante 30 días. Al cabo de este tiempo las latas se abrieron y se determinó la firmeza del contenido de cada lata. Los datos fueron los siguientes: Pectina: Firmeza: 0% 50.5, 46.8 1.5% 62.3, 67.7 3% 80.1, 79.2 a. ¿Cuál es la ecuación lineal estimada? De acuerdo al gráfico, ¿sería razonable usar una línea recta para estos datos? b. Formule y pruebe las hipótesis de interés usando =.05. c. ¿Es posible predecir la firmeza promedio que se obtendría usando 2% de pectina?, ¿y usando 6% de pectina? Si su respuesta es afirmativa, obtenga el valor predicho. De lo contrario, justifique. d. Construya un intervalo de confianza del 90% para 0. Interprete este intervalo en términos del problema. 2. A efectos de estimar la productividad de un bosque, se desea estudiar la relación entre el área basal de un árbol (x, en m2) y el volumen maderable del mismo (y, en m3). Se obtuvo una muestra aleatoria de 12 árboles y para cada árbol se midió el área basal y el volumen maderable luego de cortado. X Y .3 6 .5 9 .4 7 .9 19 .7 15 .2 5 .6 12 .5 9 .8 20 .4 9 .8 18 .6 13 a. Indique e interprete el coeficiente de correlación lineal. b. Conduzca un análisis de regresión lineal. Interprete (si fuese posible) los estimadores del intercepto y de la pendiente en términos de este problema. Formule y pruebe las hipótesis de interés usando =.01. Indique sus conclusiones. 3. En el archivo de InfoStat reglin (que lo encontrará en Program Files>InfoStat>Datos) se encuentran datos que estudian la relación entre el pH del medio de cultivo y la biomasa producida (en g). a. b. c. d. Grafique los datos. Estime la ecuación de regresión. Formule y pruebe las hipótesis apropiadas de regresión lineal. Interprete, si fuese posible, los estimadores del intercepto y de la pendiente en términos de este problema. e. Construya un intervalo de confianza del 99% para 1. 37 Laboratorio 13 4. Generalmente se considera que las personas más altas son mejores jugadores de baloncesto porque son más capaces de introducir la bola en la canasta. Los datos que aparecen en la tabla basquetbol (en la página del curso) muestran las alturas de 25 atletas que no son jugadores de baloncesto y el número de bolas que pudieron colocar en un periodo de 60 segundos. a. Conduzca un análisis de regresión lineal que permita corroborar o no esta afirmación. b. Interprete (si fuese posible) los estimadores del intercepto y de la pendiente en términos de este problema. c. Formule y pruebe las hipótesis de interés usando =.01. Indique sus conclusiones. d. Prediga, si es posible, la cantidad de bolas que colocaría un jugador de 60” de altura y uno de 77” de altura. 38 Laboratorio 14 Laboratorio 14: Diseño en bloques completos aleatorizados 1. Se condujo un experimento para comparar los efectos de tres diferentes insecticidas en habichuela. Se usaron cuatro bloques, cada uno con 3 hileras (= unidades experimentales) a una distancia adecuada. Cada hilera se plantó con 100 semillas y se mantuvo bajo uno de los tratamientos con insecticida. Los insecticidas se asignaron aleatoriamente a las hileras de forma tal que cada insecticida se aplicó a una hilera de cada bloque. La respuesta de interés fue el número de plántulas emergidas en cada hilera. Insecticida A B C Bloque 1 56 84 80 Bloque 2 49 78 72 Bloque 3 65 94 83 Bloque 4 60 93 85 a. Prepare una tabla de ANOVA en InfoStat. b. Formule y pruebe las hipótesis de interés. Use α=0.05. Indique sus conclusiones en términos de este problema. c. ¿Cómo se hubiese realizado la asignación de los tratamientos a las unidades experimentales si el diseño hubiese sido completamente aleatorizado? Describa brevemente. d. Realice, de ser necesario, una prueba de DMS para comparar los tratamientos. Use α=0.05. Indique sus conclusiones. e. Grafique los resultados. f. Construya un intervalo de confianza para la media del tratamiento A. 39 Laboratorio 14 2. Se desea estudiar el efecto de cuatro nematicidas sobre el rendimiento de plátano. Para ello se dispone de 16 parcelas que están dispuestas en el campo de la siguiente manera: Se espera que las parcelas que estén más abajo reciban más humedad en el suelo que las que estén más arriba (por ejemplo, las parcelas 9-12 van a tener más humedad que las parcelas 1-4). a. ¿Qué diseño experimental recomendaría para este experimento? Justifique brevemente. b. Asigne los nematicidas a las parcelas aleatoriamente (de acuerdo al diseño escogido en a). Escriba el código de tratamiento asignado (N1, N2, N3 o N4) dentro de cada parcela. c. Presente una tabla con las fuentes de variación y los grados de libertad (en números). 3. Para comparar cuatro preparaciones diferentes realizadas con harina de ñame, un panel de 12 jueces realizará una evaluación sensorial de los alimentos ofrecidos. Cada juez probará las cuatro preparaciones, en un orden aleatoriamente escogido (diferente para cada juez). Luego de probar el alimento, el juez le da un score entre 1 y 10. Los datos están disponibles en la página del curso. Juez 1 1 1 1 2 … 12 12 Prep 4 3 1 2 4 … 1 2 Score 4 4 4 5 5 … 9 8 a. Prepare una tabla de ANOVA en InfoStat. b. Formule y pruebe las hipótesis de interés. Use α=0.05. Indique sus conclusiones en términos de este problema. 40