PROBLEMA 1 (3 puntos) En el amplificador de la figura calcular: a
Anuncio

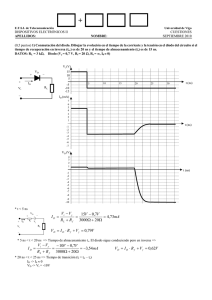
PROBLEMA 1 (3 puntos) En el amplificador de la figura calcular: a) La ganancia de tensión (AV = vo/vi) y la ganancia total de tensión (AVS = vo/vs) a frecuencias medias (1 punto) b) La ganancia de corriente (AI = io/ii) a frecuencias medias (0,5 puntos) c) La resistencia de entrada y resistencia de salida a frecuencias medias (0,5 puntos) d) La frecuencia de corte inferior aproximada. (0,5 puntos) e) La frecuencia aproximada de corte superior (0,5 puntos) C3 -> ∞ RS = 500 Ω RL = 100 kΩ Datos: C1 = C2 = 5 µF Transistores bipolar: hfe = 50 hie = 1,5 kΩ rd = 200 kΩ Cgs = 100 nF Cgd =100 pF FET: gm = 10 mA/V +V 10K ii + vi vS io 100K C1 RS 1K + vo 10K 680Ω RL C2 470Ω 1M C3 _ _ Ro Ri a) Circuito equivalente a frecuencias medias: RS ii + vS vi hie io ib + hfe⋅ ib 100K//10K ≈ 9K + vo vgs 10K 680Ω 1M gm⋅ vgs rd 1K RL _ _ _ Ri Ro v0 = − g m ⋅ v gs ⋅ ((rd // 1K ) // R L ) = − g m ⋅ v gs ⋅ ((200 K // 1K ) // 100 K ) = − g m ⋅ v gs ⋅ 0,985 K = − 10 ⋅ v gs ⋅ 0,985 = −9,85 ⋅ v gs v i = ib ⋅ hie + (1 + h fe ) ⋅ ib ⋅ (680Ω // 1M ) ⇒ ib ≈ vi hie + (1 + h fe ) ⋅ 680Ω v gs = v i − hie ⋅ ib = v i − hie ⋅ AV = vi = vi hie + (1 + h fe ) ⋅ 680Ω 9,85 ⋅ v gs v gs v0 =− vi ⎛ ⎞ hie ⎜1 − ⎟ ⎜ h + (1 + h ) ⋅ 680 ⎟ ie fe ⎝ ⎠ AVS = ⎛ ⎞ hie ⎟ ⋅ ⎜1 − ⎜ ⎟ ( ) + 1 + ⋅ 680 Ω h h ie fe ⎝ ⎠ ⎛ ⎞ hie ⎞ 1500 ⎟ = −9,85 ⋅ ⎛⎜1 − ⎟⎟ = −9,44 = −9,85 ⋅ ⎜1 − ⎜ ⎜ h + (1 + h ) ⋅ 680 ⎟ ( ) 1500 + 1 + 50 ⋅ 680 ⎝ ⎠ ie fe ⎝ ⎠ v0 v = AV ⋅ i vs vs vi Ri = v s Rs + Ri ib ⋅ hie + (1 + h fe ) ⋅ ib ⋅ 680 hie + (1 + h fe ) ⋅ 680 vi = = 9000 ⋅ = hie + (1 + h fe ) ⋅ 680 ii hie + (1 + h fe ) ⋅ 680 + 9000 + ib ib ⋅ 9000 1500 + (1 + 50 ) ⋅ 680 9000 ⋅ = 7207,17Ω 1500 + (1 + 50 ) ⋅ 680 + 9000 Ri 7207,17 AVS = AV ⋅ = −9,44 ⋅ = −8,82 Rs + Ri 500 + 7207,17 Ri = AV = -9,44 AVS = -8,82 b) Ganancia de corriente: v0 i v R R 7207,17 AI = 0 = L = 0 ⋅ i = −9,44 ⋅ = −0,68 vi ii 100000 vi R L Ri AI = -0,68 c) La resistencia de entrada ya se calculó en el apartado a y su valor es Ri = 7207,17 Ω. Para calcular la resistencia de salida se debe cortocircuitar la señal de entrada, es decir, vs = 0. Esto implica que ib = 0 y por lo tanto vgs = 0. Analizando el circuito de salida con vgs = 0 queda que la resistencia de salida es: 1K ⋅ 200 K = 995Ω R0 = 1K // rd = 1K + 200 K Ri = 7207,17 Ω R0 = 995 Ω d) La frecuencia de corte inferior viene limitada por los condensadores C1 y C2 (C3 al tener un valor muy grande situara un polo muy cercano a la frecuencia cero). Calculamos la resistencia que ve el condensador C1: RC1 = Rs + Ri = 500Ω + 7207,17Ω = 7707,17Ω Y ahora calculamos la frecuencia aproximada del polo que introduce este condensador: 1 1 f P1 = = = 4,13Hz 2 ⋅ π ⋅ RC1 ⋅ C1 2 ⋅ π ⋅ 7707,17Ω ⋅ 5 ⋅ 10 −6 F Hacemos lo mismo con el condensador C2: RC 2 = 1M + (680Ω // R X ) donde RX es la resistencia vista desde el emisor del transistor bipolar hacia la entrada. v RX = x ix v x = −ib ⋅ hie − ib ⋅ (9 K // RS ) i x = −(1 + h fe ) ⋅ ib h + (9 K // RS ) R X = ie = 1 + h fe 9000 ⋅ 500 9000 + 500 = 38,69Ω 1 + 50 1500 + 680 ⋅ 38,69 ≈ 1M 680 + 38,69 1 1 = = = 31,83mHz 6 2 ⋅ π ⋅ RC 2 ⋅ C 2 2 ⋅ π ⋅ 10 ⋅ 5 ⋅ 10 −6 RC 2 = 10 6 + f P2 Por lo tanto fP1 es el polo dominante y es el que marca la frecuencia de corte inferior. fL ≈ fP1 ≈ 4,13 Hz e) El circuito equivalente a altas frecuencias sería el siguiente: RS ii + vS vi hie ib Cgd hfe⋅ ib 100K//10K ≈ 9K 10K 680Ω 1M Cgs gm⋅ vgs rd 1K RL _ Cada una de las capacidades del FET introduce un polo a alta frecuencia. Para analizar este circuito se aplica Miller quedando el siguiente circuito equivalente: RS ii hie hfe⋅ ib + vS ib 100K//10K ≈ 9K vi 10K 680Ω 1M C’gs gm⋅ vgs C’gd rd 1K RL _ Donde: C ' gs = C gs + C gd ⋅ (1 − K ) 1⎞ ⎛ C ' gd = C gd ⋅ ⎜1 − ⎟ ⎝ K⎠ A frecuencias medias K = v d − g m ⋅ v gs ⋅ (rd // 1K // RL ) = = − g m ⋅ (rd // 1K // RL ) = −9,85 vg v gs C ' gs = 100nF + 0,1nF ⋅ (1 + 9,85) = 101,08nF 1 ⎞ ⎛ C ' gd = 0,1nF ⋅ ⎜1 + ⎟ = 0,11nF ⎝ 9,85 ⎠ Ahora se calculan las resistencias vistas por los respectivos condensadores teniendo en cuenta que cuando se trabaja con un condensador los demás se consideran circuitos abiertos. RC ' gs = (1M // 680Ω // R X ) = (1M // 680Ω // 38,69Ω ) = 36,6Ω RC ' gd = (rd // 1K // R L ) = 985,19Ω Los valores aproximados de las frecuencias de os polos introducidos por cada capacidad son: f P1 = f P2 = 1 2 ⋅ π ⋅ RC ' gs ⋅ C ' gs 1 2 ⋅ π ⋅ RC ' gd ⋅ C ' gd = = 1 ≈ 43kHz 2 ⋅ π ⋅ 36,6Ω ⋅ 101,08 ⋅ 10 −6 F 1 = 1468,6kHz 2 ⋅ π ⋅ 985,19Ω ⋅ 0,11 ⋅ 10 −6 F El fP1 es un polo dominante y es el que marca la frecuencia de corte superior. fH ≈ fP1 ≈ 43 kHz PROBLEMA 2 (3 puntos) Dado el siguiente amplificador basado en un transistor bipolar en configuración de colector común, calcular: a) La ganancia de tensión a frecuencias medias (1 punto) b) La respuesta (Vo/Vi) en baja frecuencia (1 punto) c) Dibujar el diagrama de bode del módulo (1 punto) Datos: hfe= 219, ro= hoe-1 = 8480 Ω, hie= 552 Ω, RB= 10 kΩ, RE= 1300 Ω, RL= 50 Ω, CE= 100 µF, CB= 10 nF. + Vi + CB VCC 15 Vdc Q1 10 nF CE RB 10 kΩ Vo 100 µF RL 50 Ω RE 1300 Ω + VEE 15 Vdc Solución del apartado a). Respuesta a frecuencias medias: Para obtener la respuesta del amplificador a frecuencias medias se utiliza su circuito equivalente de pequeña señal de la Figura 1. La resistencia de salida ro del transistor, la resistencia RE de polarización y la de carga RL, se pueden sustituir por una resistencia Ro equivalente al paralelo de las tres, tal y como se muestra en (1). De este modo, la tensión de salida viene dada por (2). Además, la corriente de base se obtiene con (3), a partir de la caída de tensión en la resistencia hie de entrada del transistor. Vi hie B E + Vi h fe ⋅ ib RB Vo ro RE RL C Ro Figura 1. Circuito equivalente de pequeña señal a frecuencias medias. Ro = 1 = 47.87 Ω 1 1 1 + + ro RE RL (1) Vo = (i B + h fe ⋅ i B )⋅ Ro = i B ⋅ (1 + h fe )⋅ Ro (2) Vi − Vo (3) iB = hie Ahora, con (2) y (3), se obtiene la expresión (4), que relaciona la tensión de entrada y la de salida, y que proporciona la expresión buscada de la ganancia a frecuencias medias (5). Tal y como era de esperar, la esta ganancia es ligeramente inferior a la unidad. Vo = Vi − Vo ⋅ (1 + h fe )⋅ Ro hie Vo = Vi 1 + (4) Ro ⋅ (1 + h fe ) 1 47.87 ⋅ (1 + 219) = = = 0.95 hie Ro ⋅ (1 + h fe ) + hie 47.87 ⋅ (1 + 219) + 552 Ro ⋅ (1 + h fe ) (5) Solución apartado b). Respuesta a frecuencias bajas, opción 1: Ahora, para estudiar la respuesta a baja frecuencia se utiliza el circuito equivalente de pequeña señal de la Figura 2, en el que se consideran las capacidades de acoplo CB y CE. Cada una de estas capacidades introduce un cero en el origen (están en serie con el camino de la señal) y un polo, para cuyo cálculo se tendrán en cuenta las resistencias equivalentes vistas desde cada una de las citadas capacidades. Vi CB hie B + Vi CE E h fe ⋅ ib RB ro RE Vo RL C Rx Figura 2. Circuito equivalente de pequeña señal del amplificador en colector común. Para evaluar el efecto de CB se calcula la resistencia equivalente que se ve desde sus bornes. Según el esquema de la Figura 3, esta resistencia será el paralelo de RB con la resistencia equivalente Rx, teniendo en cuenta que para ver el efecto de CB se considera CE en cortocircuito. ix hie + h fe ⋅ ix vx Ro C Figura 3. Circuito equivalente para calcular la resistencia equivalente Rx que resulta en paralelo con RB. Vo = i x ⋅ (1 + h fe )⋅ Ro (6) Vx − Vo = ix hie V x = i x ⋅ hie + Ro ⋅ (1 + h fe ) [ Rx = f pCB (7) ] Vx = hie + Ro ⋅ (1 + h fe ) = 552 + 47.87 ⋅ (1 + 219) = 11 083.4 Ω ix 1 1 = = = 3 027 Hz 2 ⋅ π ⋅ CB ⋅ (RB // Rx ) 2 ⋅ π ⋅10 ⋅10 −9 ⋅ 5 256.9 (8) (9) (10) Para evaluar el efecto de CE, también se supone la otra capacidad, o sea, CB, en cortocircuito. Ahora el circuito equivalente útil para calcular la resistencia que ve el condensador CE es el siguiente. B ib C h fe ⋅ ib hie ro E CE Vo RE RL Figura 4. Circuito equivalente para calcular la resistencia que se ve desde el condensador de salida CE. En el circuito de la Figura 4, como la resistencia de salida del transistor está entre emisor y masa, se puede poner en paralelo con RE, tal y como muestra la Figura 5. B ib C h fe ⋅ ib hie Rx Vx CE ix RE Vo ro RL Figura 5. Circuito equivalente para calcular la resistencia que se ve desde el terminal de emisor. Siguiendo el esquema de la Figura 5 se calcula la resistencia vista desde el emisor con el par de expresiones (11) y (12), de las cuales se deduce (13), la cual da una resistencia equivalente de 2.509 Ω. Finalmente, la resistencia vista desde CE es, según (14), la suma de la de carga RL con el paralelo de la de salida del transistor ro, la resistencia equivalente vista desde el emisor Rx, y RE. (11) ib ⋅ hie = −Vx (12) − i x = ib ⋅ (1 + h fe ) Vx h 552 = Rx = ie = = 2.509 Ω ix 1 + h fe 220 1 = 52.5 Ω 1 1 1 + + 2.509 8 480 1 300 Por tanto, la frecuencia del polo que aporta CE está dada por (15). 1 1 = = 30.31 Hz f pCE = 2 ⋅ π ⋅ CB ⋅ RCE 2 ⋅ π ⋅100 ⋅10 −6 ⋅ 52.5 RCE = RL + (Rx // ro // RE ) = 50 + (13) (14) (15) Solución apartado b). Respuesta a frecuencias bajas, opción 2: Cabe destacar que se ha considerado para el cálculo de la frecuencia del polo de CE que la capacidad CB es un cortocircuito, pero, teniendo en cuenta que el polo de CB está dos décadas por encima, sería más aproximado suponer que a 30 Hz la capacidad de acoplo de entrada CB es un circuito abierto, ya que está muy lejos de los 3 027 Hz. Así, de esta forma se consideraría el circuito equivalente de la Figura 6. Ahora RB está en serie con hie, es decir, hay que sumarsela, ya que al considerar CB un circuito abierto, al sustituir por un corto el generador de entrada, este último ya no cortocircuita a la resistencia RB, como sucedía en la opción 1 anterior. B RB C ib h fe ⋅ ib hie Rx Vx CE ix Vo ro RE RL Figura 6. Circuito equivalente de la opción 2. A frecuencias por debajo de 300 Hz (una década por debajo del polo introducido por la capacidad CE), la capacidad de acoplo de entrada se considera con una impedancia muy elevada, concretamente, a 30 Hz tiene una impedancia de 530 kΩ. Vx h + RB 10 552 (16) = Rx = ie = = 47.96 Ω 1 + h fe 220 ix 1 = 74 Ω (17) 1 1 1 + + 47.96 8 480 1 300 Por tanto, la frecuencia del polo que aporta CE, considerando CB un circuito abierto, está dada por (15). 1 1 (18) = = 66.2 Hz f pCE = 2 ⋅ π ⋅ CB ⋅ RCE 2 ⋅ π ⋅100 ⋅10 −6 ⋅ 74 RCE = RL + (Rx // ro // RE ) = 50 + Vi 1Vac 0Vdc V1 15Vdc Q1 C3 Q2N2222 10nF C2 V3 Vo R4 10k 0 100uF 0 0 R3 50 R2 1300 V2 15Vdc 0 Figura 7. Esquema del amplificador simulado con OrCAD PSpice. 0 (3.388 kHz, -3.03 dB) (33.48 Hz, -40.58 dB) -50 (66.28 Hz, -33.94 dB) -100 1.0 Hz 10 Hz DB(V(Vo)/V(Vi)) 100 Hz 1.0 kHz 10 kHz 100 kHz 1.0 MHz Frequency Figura 8. Gráfica de la respuesta en baja frecuencia del amplificador en colector común acoplado en alterna.