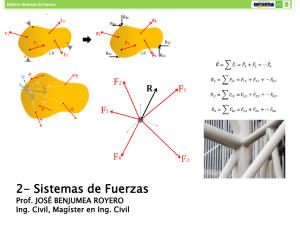
Equilibrio de Cuerpo Rígidos
Anuncio

Estática- Equilibrio del Cuerpo Rígido 3- Equilibrio del Cuerpo Rígido (Sistemas Coplanares) Prof. JOSÉ BENJUMEA ROYERO Ing. Civil, Magíster en Ing. Civil Estática- Equilibrio del Cuerpo Rígido Contenido 3. Equilibrio de cuerpos rígidos 3.1 Diagrama de cuerpo libre. 3.2 Equilibrio en el plano. Reacciones en apoyos y conexiones de una estructura bidimensional. 3.3 Reacciones estáticamente indeterminadas. Restricciones parciales en cuerpos rígidos. 3.4 Equilibrio de un cuerpo sometido a dos fuerzas. Equilibrio de un cuerpo sometido a tres fuerzas. . . . Estática- Equilibrio del Cuerpo Rígido Equilibrio de Cuerpo Rígidos T1 T2 P W3 W4 Q W2 W1 Reduciendo las fuerzas externas a un sistema fuerza-par en O O http://www.modelmotor.es/tienda-a/13-801066/ficha/Grua-Torre-Wolff-7532-cross-187-Ros-Agritec.html Estática- Equilibrio del Cuerpo Rígido T1 T2 P W3 W4 Q W2 W1 Separando el C.R. del suelo ºO http://www.modelmotor.es/tienda-a/13-801066/ficha/Grua-Torre-Wolff-7532-cross-187-Ros-Agritec.html Estática- Equilibrio del Cuerpo Rígido T1 T2 P W3 W4 Q W2 W1 El sistema estará en equilibrio sí: R*=0 y MR*=0 ΣFx=0, ΣFy=0, ΣFz=0 ΣMx=0, ΣMy=0, ΣMz=0 O http://www.modelmotor.es/tienda-a/13-801066/ficha/Grua-Torre-Wolff-7532-cross-187-Ros-Agritec.html Estática- Equilibrio del Cuerpo Rígido ¿Qué aprenderemos en esta parte del curso? - Diagrama del cuerpo libre - Tipos de restricciones - ¿La estructura está apoyada apropiadamente? - ¿La estructura puede ser calculada mediante la estática? - Establecer las condiciones para que un estructura esté en equilibrio Equilibrio Coplanar Equilibrio no Coplanar Estática- Equilibrio del Cuerpo Rígido 3.1 Diagrama de Cuerpo Libre (1) Identifique el C.R. separarlo del suelo, de las uniones, apoyos y de otros cuerpos (2) Identifique y dibuje todas las fuerzas externas Fuerzas aplicadas y reacciones Incluya el peso Si el C.R. está formado por varias partes no incluya las fuerzas que esas partes ejercen entre sí. Lo anterior, siempre que estudie el equilibrio del cuerpo rígido completo cable (3) Determine la magnitud y dirección de las acciones conocidas (Fuerzas y Momentos) (4) Identificar las fuerzas desconocidas (generalmente son las restricciones) (5) Verificar que el D.C.L tenga las dimensiones necesarias !Dibuje el sistema de referencia! Estática- Equilibrio del Cuerpo Rígido 3.2 Equilibrio Coplanar 3.2.1 Tipologías de Reacciones (Restricciones) Tomado de [Meriam & Kraige, 2002] Engineering Mechanics STATICS, fifht Edition, Jhon Wiley & Sons. Estática- Equilibrio del Cuerpo Rígido Tomado de [Meriam & Kraige, 2002] Engineering Mechanics STATICS, fifht Edition, Jhon Wiley & Sons. Estática- Equilibrio del Cuerpo Rígido + torsion Spring Tomado de [Meriam & Kraige, 2002] Engineering Mechanics STATICS, fifht Edition, Jhon Wiley & Sons. Estática- Equilibrio del Cuerpo Rígido Simplified seismic analysis procedures for elevated tanks considering fluid–structure–soil Interaction (R. Livaoğlua, , , A. Doğangünb, ) http://www.sciencedirect.com/science/article/pii/S0889974606000041#gr1 Estática- Equilibrio del Cuerpo Rígido Propuesta de Diseño Nuevo Estadio de Barrancabermeja Estática- Equilibrio del Cuerpo Rígido Estática- Equilibrio del Cuerpo Rígido Apoyo en puente San Francisco – Oakland Bay Estática- Equilibrio del Cuerpo Rígido Apoyo en puente peatonal Metrolínea – Estación Hormigueros Estática- Equilibrio del Cuerpo Rígido Roller Support Fuente: http://ceephotos.karcor.com/2011/09/23/roller-support/ Estática- Equilibrio del Cuerpo Rígido Roller Support Estática- Equilibrio del Cuerpo Rígido Roller Support Fuente: http://minnesota.publicradio.org/display/web/2009/03/25/bridgecollapse_update/ Estática- Equilibrio del Cuerpo Rígido Elastomeric Support Puente de vía ferroviaria AHK11 Fuente: http://www.zt-ron.at/es/proyectos/puente-ahk11.html Estática- Equilibrio del Cuerpo Rígido Base Plates (Platinas Bases) Fuente: http://www.amtecdesigns.com/Struct.html Estática- Equilibrio del Cuerpo Rígido Otros ejemplos de soportes [Hibbeler] [Beer} Estática- Equilibrio del Cuerpo Rígido Ejercicio 1 Dibuje el D.C.L de las siguientes estructuras. Estática- Equilibrio del Cuerpo Rígido Ejercicio 2 Dibuje el D.C.L de la viga ABC. Asuma pasadores sin fricción. D P A B C Estática- Equilibrio del Cuerpo Rígido Ejercicio 3 Dibuje el D.C.L de la viga ABC. Asuma pasadores sin fricción. P A B C Estática- Equilibrio del Cuerpo Rígido ¿En qué dirección se asumen las reacciones? P P P w B 10 m A Estática- Equilibrio del Cuerpo Rígido ¿Puedo resolver la estructura con lo aprendido en el curso de estática? ¿La estructura es estable para cualquier valor de P, Q, R, S y W ? P W Q R S Estática- Equilibrio del Cuerpo Rígido 3.2.2 Ecuaciones de equilibrio C D B A C Significado Físico de las ecuaciones de Equilibrio vs Sistemas Linealmente Independendientes A B Tratar de buscar ecuaciones que tengan una sola incógnita: -Momento respecto a ejes - Momento respecto a puntos que están dentro de la línea de acción de la incógnita -Momento respecto a puntos de convergencia Estática- Equilibrio del Cuerpo Rígido Conjunto de ecuaciones INDEPENDIENTES (disponibles)… 1. ΣFx=0, ΣFy=0, ΣMo=0 2. ΣFx’=0, ΣFy’=0, ΣMa=0 (x’ y y’ no son paralelos entre sí) R R MR A x y y x x ΣMa=0 R└ a y’ └ MR=0 R└ a x’ └ y R Estática- Equilibrio del Cuerpo Rígido 3. ΣMa=0, ΣMb=0, ΣFy’=0 R B ΣMa=0 ΣMb=0 R y ¿condición del eje AB y del eje y’? y A x ΣFy’=0 x 4. ΣMa=0, ΣMb=0, ΣMc=0 C B C y y A x a, b y c NO COLINEALES R A B ¿R puede ser diferente de cero (0)? x Si a, b y c son COLINEALES Estática- Equilibrio del Cuerpo Rígido Para el caso de Fuerzas Concurrentes en O 5. ΣFx’=0, ΣFy’=0 6. ΣMa=0, ΣMb=0 R B O O y y R x x 7. ΣFx’=0, ΣMa=0 O y A x A Estática- Equilibrio del Cuerpo Rígido Para el caso de Fuerzas Paralelas (aplicadas en dirección del Eje y) 8. ΣMa=0, ΣFy’=0, y’ no paralela al eje x MR y ΣMa=0 A MR=0 x 9. ΣMa=0, ΣMb=0 B y A x Línea AB no paralela al eje x Estática- Equilibrio del Cuerpo Rígido 3.2.3 Reacciones Estáticamente Indeterminadas y Restricciones Inadecuadas Analizar cada una de las siguientes estructuras P P P Q Q Q W Estructura Estáticamente Determinada Estructura Completamente Restringida P Q Q W Q Estructura Estáticamente Indeterminada (estructura hiperestática) Estructura Completamente Restringida Estática- Equilibrio del Cuerpo Rígido P Q Q Q W Estructura Estáticamente Inestable Estructura Restringida Parcialmente W Q Q W Q Estructura Estáticamente Indeterminada Estructura Impropiamente Restringida* Estructura Estáticamente Indeterminada Estructura Impropiamente Restringida* * También llamada Inestabilidad Geométrica Estática- Equilibrio del Cuerpo Rígido Q Q W W Q “Un C.R. está impropiamente restringido siempre que los apoyos, aunque proporcionen un numero suficiente de reacciones, estén ubicados de tal forma que las reacciones son concurrentes o paralelas” Estática- Equilibrio del Cuerpo Rígido ¿Un C.R. está impropiamente restringido no sirve para nada? Q Q W W Q Estática- Equilibrio del Cuerpo Rígido Ejercicio 4-a Conexiones: rodillos, pasadores sin fricción, bielas lisas ¿impropia, completa o parcialmente restringida? ¿estáticamente determinada o indeterminada? ¿se mantiene el equilibrio de la estructura? AB= 3m, BC= 2m, CD=2 m Estática- Equilibrio del Cuerpo Rígido Ejercicio 4-b Estática- Equilibrio del Cuerpo Rígido Ejercicio 5 Todas la estructuras presentadas son hiperestáticas. Describir al menos una modificación de los apoyos para cada caso que convierta en isostática la estructura correspondiente. Estática- Equilibrio del Cuerpo Rígido 3.2.4 Cuerpos de 2 y 3 Fuerzas - Cuerpos de 2 Fuerzas P Mo Q “Un C.R. sometido a fuerzas que actúan únicamente en dos puntos, es un cuerpo de dos fuerzas” Estática- Equilibrio del Cuerpo Rígido - Cuerpos de 3 Fuerzas “Un C.R. sometido a fuerzas que actúan únicamente en tres puntos, estará en equilibrio si las fuerzas convergen en un solo punto ó si son paralelas” Q B F A O C P Excepción: cuando las fuerzas no se intersecan y son paralelas ΣMo=0 Estática- Equilibrio del Cuerpo Rígido B P d F A O d C P ΣMo=0 ¿ΣFx=0? Estática- Equilibrio del Cuerpo Rígido Ejercicio 6 Tomado de MIT OpenCourseWare , Civil and Environmental Engineering 1.050 Solid Mechanics, Fall 2004 Estática- Equilibrio del Cuerpo Rígido Ejercicio 7 Idealización de un puente levadizo … Prop. Puente Laureano Gómez (Barranquilla, COL) http://www.skyscraperlife.com/infraestructura-de-transporte/7954-nuevo-puente-pumarejo-sobre-el-rio-magdalena-barranquilla-colombia.html Puente Levadizo en Galicia, ESP http://www.galiciaenfotos.com/leca-y-matosinhos-i/ Estática- Equilibrio del Cuerpo Rígido O de etapas constructivas (Construcción Estación Terminal Trenes, Berlín) Fuente http://es.wikiarquitectura.com/index.php/Estaci%C3%B3n_Central_de_trenes_de_Berl%C3%ADn Estática- Equilibrio del Cuerpo Rígido Determine las reacciones en los apoyos de la armadura (que representa un estado constructivo). El apoyo en C, es de segundo orden (pasador sin fricción). Estática- Equilibrio del Cuerpo Rígido Ejercicio 8 Determine las reacciones en los apoyos de la barra rígida ABC. El elemento CD es un eslabón corto. Estática- Equilibrio del Cuerpo Rígido Ejercicio 8a Estática- Equilibrio del Cuerpo Rígido Ejercicio 8b Estática- Equilibrio del Cuerpo Rígido Ejercicio 9 La barra AB se somete a una fuerza P en el punto B. En el extremo A se encuentra un apoyo de segundo orden. En B se une a un resorte de constante K que pasa a través de una polea sin rozamiento. Cuando θ=0 (AB horizontal), el resorte no se encuentra esforzado. Hallar una expresión para θ, sabiendo que la barra AB se encuentra en equilibrio. L Ө B K P A Estática- Equilibrio del Cuerpo Rígido Ejercicio 9a Estática- Equilibrio del Cuerpo Rígido Ejercicio 10 La barra rígida ACB esta apoyada en C mediante 1 apoyo de segundo orden. En los extremos A y B, se suspende de un cable que pasa por una polea sin rozamiento en D. Calcular la reacción en C y la tensión en el cable debido a la fuerza P=150 N. m m P m m Estática- Equilibrio del Cuerpo Rígido Ejercicio 11 Una barra uniforme AB, de longitud igual a 2R, y peso W, se apoya en el interior de un recipiente semi-esférico de radio R. Determine el ángulo teta correspondiente a la posición de equilibrio de la barra. Asuma que la superficie no tiene fricción. 𝐵 𝐴 𝜃 Hint: Teorema de Tales de Mileto Estática- Equilibrio del Cuerpo Rígido Segundo Teorema de Tales de Mileto Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo. Estática- Equilibrio del Cuerpo Rígido Estática- Equilibrio del Cuerpo Rígido Ejercicio 11a En la figura, del punto O cuelgan una esfera de radio r y peso G, por medio de un hilo de longitud b, y una barra uniforme de longitud 2a y peso W que se apoya contra la esfera. Determine el ángulo α de equilibrio que el hilo forma con la vertical. Estática- Equilibrio del Cuerpo Rígido Ejercicio 12 La barra AB soporta una fuerza de 200 N, se encuentra suspendida de un cable en el vértice B y apoyada en A. Calcular la tensión del cable y la reacción en A Estática- Equilibrio del Cuerpo Rígido Ejercicio 13 La viga horizontal está soportada por resortes en sus extremos. Si la rigidez del resorte situado en A es KA= 5kN/m, determine la rigidez requerida en el resorte ubicado en B de manera que si la viga es cargada con la fuerza de 800 N, permanezca en posición horizontal antes y después de la carga. Estática- Equilibrio del Cuerpo Rígido Ejercicio 14 Determine the angle α and the magnitudes of the reactions at A and B. Assume that 0 ≤ 𝛼 ≤ 90° DO NOT USE EQUATIONS OF STATIC EQUILIBRIUM! Estática- Equilibrio del Cuerpo Rígido Ejercicio 14a Estática- Equilibrio del Cuerpo Rígido Ejercicio 15 Los centros de gravedad del carro elevador (masa 50 kg) y de la caja (masa 120 kg) están en G1 y G2, respectivamente. El camión debe poder subir el escalón de 5 mm cuando la fuerza P de empuje es de 600 N. Encuentre el mínimo radio permisible para la rueda en A. ¿Se volteará el carro para las cargas asumidas? (Medidas en mm) 375 P 1200 G2 C B A 700 500 5 G1 Estática- Equilibrio del Cuerpo Rígido Ejercicio 15a Un ingeniero de seguridad desea realizar pruebas para conocer la carga máxima (WL) que puede levantarse mediante la máquina elevadora sin que ocurra vuelco. Con el fin de evitar accidentes que puedan afectar la integridad del ingeniero, la empresa lo contrató a usted para determinar dicha carga sin necesidad de que alguien se monte en la máquina. El peso del operador y de la máquina (WF) es de 600 kN. Estática- Equilibrio del Cuerpo Rígido Ejercicio 15b Una empresa fabricará ventiladores de piso. Los diseñadores industriales han propuesto dos opciones: un ventilador de 3 patas y otro de 4 patas. Ya que el futuro de la empresa depende del éxito de los ventiladores, el gerente lo ha contratado a usted para verificar la seguridad ante el volcamiento de ambas propuestas. h=82 cm. Para su análisis tenga en cuenta los siguientes datos: El peso combinado (motor, aspas, patas y paral) es: W3patas=87 N ; W4patas=90 N. Longitud de las patas, b=30 cm. Todas las patas tienen pequeños cauchos en sus extremos que evitan el deslizamiento (traslación) sobre la superficie. Cuando el ventilador está funcionando, las aspas ejercen una fuerza de empuje (T), la cual incrementa con la velocidad de las aspas. Desde el punto de vista de la seguridad al volcamiento, ¿cuál de los dos ventiladores tendrá un mayor éxito en el mercado? Para cada caso, las patas están espaciadas igualmente Estática- Equilibrio del Cuerpo Rígido Estática- Equilibrio del Cuerpo Rígido AD ES UN CABLE. DETERMINE LAS REACCIONES EN C Y LA TENSIÓN EN EL CABLE. Estática- Equilibrio del Cuerpo Rígido Ejercicio 16 La barra ABCD está doblada en forma de un arco circular de 4 pulgadas de rado y descansa sobre superficies sin fricción en A y D. Si el collarín colocado en B se puede mover libremente por la barra, determine a) el valor de 𝜃 para el cual la tensión en la cuerda OB es mínima, b) el valor correspondiente de la tensión, c) las reacciones en A y D Estática- Equilibrio del Cuerpo Rígido Ejercicio 17 El bloque C de peso 50 kN, descansa sobre la barra uniforme AB de peso 20 kN. El cable que \ conecta C con B pasa sobre una polea en D. Determine la magnitud de la fuerza que actúa entre el bloque y la barra. Estática- Equilibrio del Cuerpo Rígido Ejercicio 18 Una barra de longitud L y peso W, se une por uno de sus extremos a un collar en A y por el otro a una pequeña rueda en B, la cual gira libremente a lo largo de la superficie cilíndrica de radio R. Despreciando la fricción de la superficie, determine una expresión para el ángulo teta (Ɵ) que se cumpla cuando la barra esté en equilibrio Estática- Equilibrio del Cuerpo Rígido Ejercicio 19 Una barra uniforme AB de longitud l y peso W, se sostiene por dos cuerdas AC y BC de igual longitud. Demuestre que, para la posición de equilibrio, se cumple la siguiente expresión 1 senθ = 2Mo cot β 𝑊𝑙 Estática- Equilibrio del Cuerpo Rígido Ejercicio 20 La barra AB, de masa m y longitud L, se une a dos bloques en sus extremos, los cuales giran libremente por ranuras circulares. Si 𝛼 = 45°, determine: a) El valor máximo de L para que el que la barra se encuentra en equilibrio. b) Las reacciones en A y B. B 𝜶 A Estática- Equilibrio del Cuerpo Rígido Ejercicio 21 Una barra delgada uniforme de longitud L y peso W, está balanceada sobre un vaso de diámetro interno D, de superficie lisa. Determine el ángulo 𝜃 correspondiente a la posición de equilibrio. Planta Estática- Equilibrio del Cuerpo Rígido Ejercicio 22 Dos esferas pesadas, unidas entre sí por una cuerda de peso y espesor despreciable, son colgadas de una polea sin fricción y de diámetro despreciable. La polea está sostenida por un eje en el extremo volado de una barra. polea Para la posición mostrada en la figura (con la esfera más grande por encima de la pequeña), el sistema se encuentra en equilibrio estático. Determine la tensión en la cuerda y la fuerza de contacto entre las esferas. Asuma que todas las superficies son lisas. 𝑟1 = 8 𝑐𝑚, 𝑟2 = 6 𝑐𝑚 𝑤1 = 161 𝑘𝑔𝑓, 𝑤2 = 91 𝑘𝑔𝑓 1 𝐿𝑐𝑢𝑒𝑟𝑑𝑎 (𝑒𝑛𝑡𝑟𝑒 𝑐𝑒𝑛𝑡𝑟𝑜𝑠 𝑑𝑒 𝑒𝑠𝑓𝑒𝑟𝑎𝑠) = 34 𝑐𝑚 2 Nota: las esferas fueron perforadas diametralmente para que su centro de masa coincida con el centro geométrico.