Velocidad de escape
Anuncio

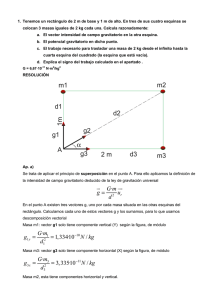
VELOCIDAD DE ESCAPE Se puede definir como la velocidad mínima necesaria para que una masa abandone un campo gravitatorio. La energía cinética adicional necesaria va a depender del estado inicial de la masa: velocidad y posición en el campo gravitatorio ( y por tanto también dependerá de estos dos factores la velocidad adicional). En lo que sigue sólo vamos a considerar una fuerza presente: la fuerza gravitatoria [despreciamos las fuerzas de fricción]. Realmente la velocidad mínima necesaria ha de ser mayor que el valor que vamos a calcular. Se trata, por tanto, de hacer que la masa abandone el campo haciendo un trabajo mínimo → → (venciendo la fuerza gravitatoria: F = − F g ) [este trabajo se puede igualar a la energía cinética mínima necesaria, obteniendo de ella la velocidad de escape]: → → F =−Fg= ∞ GMm r 2 dr W →F (r ∏ d∞) = ¶ r ∏ = − GMm r ∞ r∏ GMm r 2 r̂ = GMm r∏ = 12 mv 2e ve = 2GM r∏ Otra forma de obtener esta velocidad es igualar la energía mecánica de la masa a 0 (hemos de recordar que esta es la energía mínima necesaria para el abandono del campo): E M(m©´nima) = 1 2 2 mv e − GMm r∏ =0d ve = 2GM r∏ OBJETOS QUE YA TIENEN VELOCIDAD (v) E C tiene + E C adicional − GMm r∏ = 0 = 12 mv 2 + 12 mv 2adicional − 0 = 12 mv 2 + 12 mv 2adicional − v adicional = 2GM r∏ GMm r∏ − v2 y ve = 1 1 d 2 v 2 + 2 v 2adicional = 2GM r∏ GMm r∏ GM r∏ (v 2adicional + v 2 = v 2e ) OBJETOS EN LA SUPERFICIE DE LA TIERRA La expresión v e = km/s (j 40300 km/h). 2GM r∏ toma el valor, aproximado, para la superficie terrestre (r’ = RT) de 11,2 Los objetos sobre la superficie terrestre están girando con la Tierra y por tanto ya tienen parte de esta energía mínima necesaria (y por tanto velocidad). Si suponemos una posición ecuatorial y un radio de 6380 km (una vuelta en un día-trayectoria circular): v giro = v adicional = 2GM RT 2.6,38.10 6 24.3600 − 464 2 (un poco inferior a la calculada arriba) j 464 m/s OBJETOS EN ÓRBITA Los dispositivos en órbita ya cuentan con la velocidad orbital ( v o = v adicional = 2GM r∏ − v 2o = 2GM r∏ − GM r∏ GM r∏ d v adicional = Podemos observar que vadicional = vorbital La relación entre la velocidad orbital, la de escape y la “adicional” es: 2GM v adicional ve r∏ ve vo = 2 v orbital = 1 ; = vo = GM r∏ ). En este caso: GM r∏