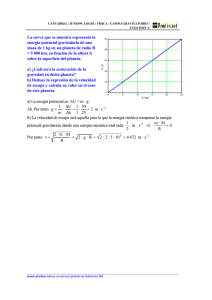
· G m g u d = · 1,334·10 / G m g N kg d = = · 3,335·10 / G m g N kg d = =
Anuncio
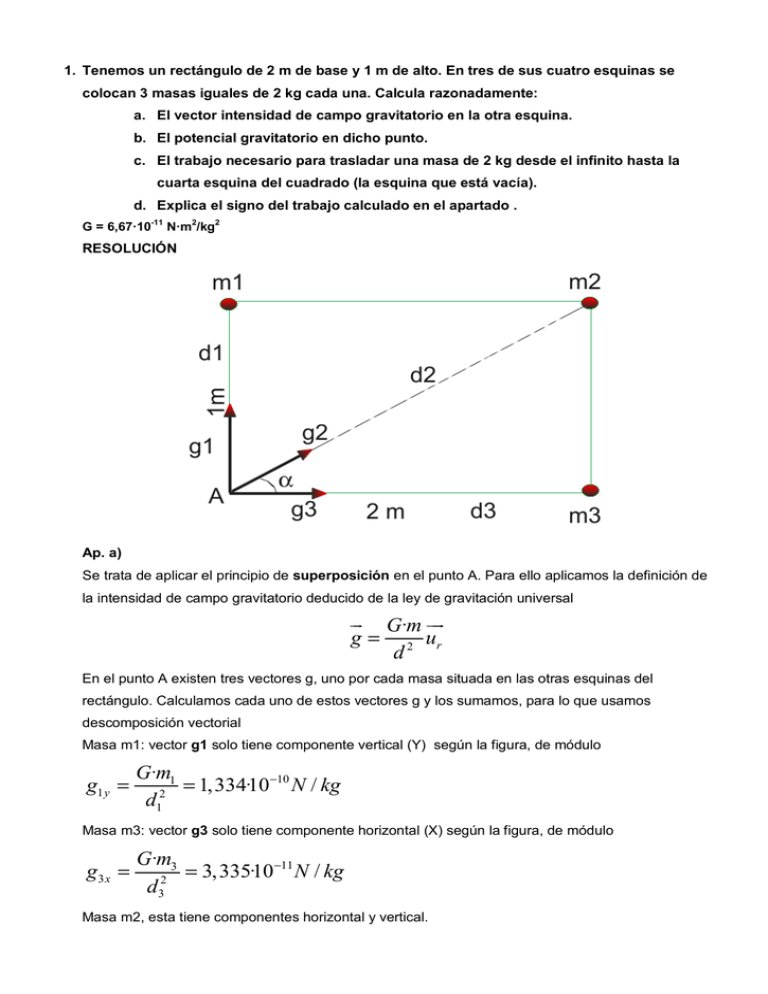
1. Tenemos un rectángulo de 2 m de base y 1 m de alto. En tres de sus cuatro esquinas se colocan 3 masas iguales de 2 kg cada una. Calcula razonadamente: a. El vector intensidad de campo gravitatorio en la otra esquina. b. El potencial gravitatorio en dicho punto. c. El trabajo necesario para trasladar una masa de 2 kg desde el infinito hasta la cuarta esquina del cuadrado (la esquina que está vacía). d. Explica el signo del trabajo calculado en el apartado . G = 6,67·10-11 N·m2/kg2 RESOLUCIÓN Ap. a) Se trata de aplicar el principio de superposición en el punto A. Para ello aplicamos la definición de la intensidad de campo gravitatorio deducido de la ley de gravitación universal G·m g = 2 ur d En el punto A existen tres vectores g, uno por cada masa situada en las otras esquinas del rectángulo. Calculamos cada uno de estos vectores g y los sumamos, para lo que usamos descomposición vectorial Masa m1: vector g1 solo tiene componente vertical (Y) según la figura, de módulo g1 y = G·m1 = 1,334·10 −10 N / kg 2 d1 Masa m3: vector g3 solo tiene componente horizontal (X) según la figura, de módulo g3 x = G·m3 = 3,335·10 −11 N / kg 2 d3 Masa m2, esta tiene componentes horizontal y vertical. d 2 = d12 + d32 = 5 m cos α = d3 2 = d2 5 senα = d1 1 = d2 5 El ángulo es el formado por la diagonal con la horizontal. La distancia d2 la calculamos por el teorema de Pitágoras g2 x = G·m2 ·cos α = 2,386·10 −11 N / kg 2 d2 g2 y = G·m2 ·senα = 1,193·10−11 N / kg 2 d2 Por tanto el vector g en el cuarto vértice es g = gx + g y g x = g 2 x + g3 x = 5, 721·10 −11 N / kg g y = g1 y + g3 y = 1, 453·10 −10 N / kg Escrito en forma vectorial es −11 −10 g = 5, 721·10 i + 1, 453·10 j N / kg Ap. b El potencial gravitatorio lo calculo por suma de potenciales debidos a cada masa que por definición Vg = − G·m d Aplicando Vg = − G·m1 G·m2 G·m3 − − = −2,598·10 −10 J d1 d2 d3 Ap. c El trabajo que es necesario aplicar (trabajo externo) lo calculamos como diferencia entre la energía potencial final e inicial. La inicial es en el infinito, por tanto es cero · g = −5,196·10 −10 J Ep A = mV Wext = Ep A − Ep∞ = Ep A = −5,196·10 −10 J Ap. d El signo negativo indica que el trabajo lo realiza el campo, es decir, el campo es el que movería a la masa. 2. En la superficie de un planeta de 1000 km de radio la aceleración de la gravedad es de 2 m/s2. Calcula razonadamente:: a. La masa del planeta. b. la energía potencial gravitatoria de un objeto de 50 kg de masa situado en la superficie del planeta c. la velocidad de escape desde la superficie del planeta G = 6,67·10-11 Nm2/kg2 RESOLUCIÓN Ap. a) Partiendo de la ley de gravitación universal sabemos que la aceleración de la gravedad (g) corresponde con intensidad de campo, cuyo módulo se calcula como g= G·M R2 Conocemos la gravedad y el radio del planeta por lo que es fácil despejar la masa del planeta g·R 2 M= = 2,998·1022 kg G Ap b) Por definición de energía potencial Ep = − G·M ·m = −108 J R Ap c) La velocidad de escape es la necesaria para que un cuerpo pueda abandonar el campo gravitatorio del planeta, es dcir, alcance distancia infinita y su energía potencial sea 0. Basta con que llegue a ese punto sin velocidad, es decir, su energía en ese punto debe ser cero. La energía potencial en el planeta más la energía cinética debe ser cero (conservación de la energía) Ep + Ec = 0 1 GMm ;v= Ec = − Ep ; mv 2 = 2 R 2·GM = 2000 m / s R O también Ep + Ec = 0 1 Ec = − Ep ; mv 2 = 108 ; v = 2 2·108 = 2000 m / s 50 3. Se pretende situar en órbita un satélite artificial de 500 kg de masa que de diariamente 12 vueltas a la Tierra. Averigua razonadamente: a. ¿A qué altura sobre la superficie terrestre se debe colocar el satélite? b. ¿Con qué velocidad debe ser lanzado para llevarlo hasta esa altura si despreciamos el rozamiento del cohete con el aire? c. ¿Cuál será la energía del satélite cuando recorre esa órbita? d. ¿Cuál será el peso del satélite en esa órbita? G = 6,67·10-11 N·m2/kg2 Masa Terrestre = 6·1024 Kg. Radio Terrestre = 6370 km RESOLUCIÓN Ap. a) Consideramos la órbita circular por lo que aplicamos la condición de equilibrio: fuerza centrípeta igual que la fuerza gravitatoria v 2 GMm m = R R2 La velocidad a la que se mueve el satélite es 12 vueltas cada día (1 día 86400 segundos) y como cada vuelta es 2·π·R metros (R radio de la órbita) 12·2π R 86400 v 2 GMm m = R R2 v= GM GM 12·2π R ; = v = 86400 R R 2 2 GM ·864002 = 8.07·106 m R= 2 (2·12·π ) 3 h = 8, 070·106 − 6,370·106 = 1, 7·106 m Ap. b) Se trata de elevar el cohete hasta la altura calculada antes. Aplicamos conservación de la energía. La energía cinética y potencial en el punto de salida debe ser igual a la del punto de llegada. Como sólo se trata de subirlo, en el de llegada su energía cinética es cero. 1 GMm GMm m·v 2 − =− 2 RT R 1 2 GM GM v − =− 2 RT R v = 2·G·M ( 1 1 − ) = 5144, 6 m / s RT R Ap c) La energía mecánica en órbita es la suma de la cinética debido a la velocidad orbital y la potencial a esa altura 1 2 GMm mv − 2 R Condición de equilibrio Em = v 2 GMm GM 2 ; m = v = R R2 R GMm Em = − = −1, 24·1010 J 2R Ap. d) El peso es la fuerza gravitatoria sobre el satélite G·M Peso = m· 2 = 3072, 7 N R