tema 10 - IES La Nía
Anuncio

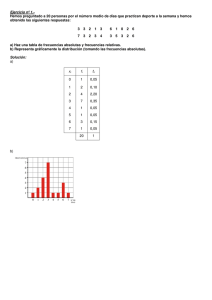
MATEMÁTICAS CC SS I ESTADÍSTICA TEMA 10: ESTADÍSTICA La Estadística es la parte de las matemáticas que se ocupa de recoger, organizar y analizar grandes cantidades de datos para estudiar alguna característica de un colectivo. 1. VARIABLES ESTADÍSTICAS UNIDIMENSIONALES 1.1. Conceptos básicos Llamamos: • Población al conjunto de todos los elementos sobre el que se realiza el estudio. • Individuo a cada uno de los elementos de la población o de la muestra. • Variable estadística unidimensional: es el resultado de una característica de la población que deseamos estudiar. Si la variable estadística unidimensional toma valores numéricos se llama cuantitativa; en caso contrario se llama cualitativa. A su vez, las variables cuantitativas se clasifican en continuas o discretas. En el primer caso la variable puede tomar cualquier valor dentro de un intervalo, mientras que en el segundo sólo puede tomar un número finito de valores. Ejemplos: 1. Si analizamos las preferencias deportivas de los alumnos de tu clase: la población es toda la clase, individuo es cada uno de los alumnos de la clase y la variable estadística es cualitativa. 2. Si estudiamos el tiempo medio que los alumnos del instituto dedican cada día a estudiar: la población es todos los alumnos del instituto, individuo es cada uno de los alumnos del instituto y la variables estadística es cuantitativa continua. 3. Si el ayuntamiento está interesado en averiguar cuántos libros saca al año de la biblioteca cada usuario, la población son todos los vecinos de la localidad socios de la biblioteca, individuo es cada uno de esos socios y la variable estadística es cuantitativa discreta. Al realizar un estudio estadístico no siempre es posible analizar a todos los individuos de la población. En estos casos se toma una muestra de la población sobre la que se observa la característica objeto del estudio. Para que el estudio sea fiable la muestra debe ser representativa del total de la población. Se llama tamaño de la muestra al número de individuos que la forman. 1.2. Tablas de frecuencias Para ordenar los datos y proceder a su análisis se utilizan las tablas de frecuencias. Una vez realizado el recuento de los resultados, construimos una tabla: en la primera columna ponemos los datos, x i , (si la variable es cuantitativa se deben poner ordenados de menor a mayor) y en la segunda el número de veces que aparece ese dato en la muestra (frecuencia absoluta, ni ). La tabla de frecuencias puede completarse con: • La frecuencia relativa, f i , es el cociente de la frecuencia absoluta y el número total de datos, N. 1/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I • • ESTADÍSTICA La frecuencia absoluta acumulada, N i , es la suma de todas las frecuencias absolutas de los valores anteriores. La frecuencia relativa acumulada, Fi , es la suma de todas las frecuencias relativas de los valores anteriores. Ejemplo1: Un equipo de baloncesto ha anotado en 20 partidos los siguientes puntos: 80, 101, 92, 80, 110, 83, 101, 75, 80, 107, 75, 85, 80, 110, 101, 92, 85, 110, 85, 80. La variable estadística es cuantitativa discreta. Vamos a construir la tabla de frecuencias: Valor xi ni Ni fi Fi Observa que: La última frecuencia absoluta acumulada, N i , es 20 y debe coincidir con el total de datos, N . La última frecuencia relativa acumulada, Fi , debe ser siempre 1. Si las frecuencias relativas se multiplican por 100 se obtienen los porcentajes. Total N=20 1 Los valores de la variable del ejemplo anterior podrían no haber presentado repeticiones y ser todos, o casi todos, diferentes. En ese caso no tendría sentido hacer una tabla con 20 valores de frecuencia absoluta 1 cada uno de ellos. Cuando la variable estadística es continua, o el número de datos del estudio es grande, conviene organizar los datos en intervalos, llamados clases. Los intervalos deben ser todos de la misma amplitud, y el punto medio de cada uno es la marca de clase. La tabla de frecuencias tiene una columna más con las marcas de clase. El extremo inferior del intervalo se toma cerrado y el superior abierto, de modo que, si un dato coincide con un extremo, pertenece al intervalo posterior Ejemplo2: Las calificaciones de 49 alumnos en una prueba son: 3; 5,5; 4,4; 6; 4,3; 7,2; 4,7; 6,5; 6,7; 4; 5,9; 5,8; 1,4; 3,2; 5,8; 4,6; 4,1; 3,5; 6,8; 5; 5,9; 2,1; 4,2; 4,5; 4,1; 4,8; 2,8; 4,7; 7,7; 6; 3; 5,7; 4,5; 4,9; 3,3; 4,8; 4,7; 7,7; 6; 3; 5,7; 4,5; 4,9; 3,3; 4,8; 4,7; 5,2; 3,8; 6,1. Vamos a agrupar los datos en 7 intervalos (se suelen poner entre 5 y 10) y a construir la tabla de frecuencias. Primero buscamos el valor mínimo: 1,4, y el valor máximo: 7,7, y calculamos su diferencia: 7,7 − 1,4 = 6,3 , este es el recorrido de la variable. Ahora dividimos el recorrido entre el nº de 6,3 intervalos: = 0,9 ≅ 1 , esto nos da la longitud de cada intervalo. 7 2/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I ESTADÍSTICA El extremo inferior del primer intervalo debe ser algo inferior al valor mínimo (1,4) y el extremo superior del último intervalo debe ser algo mayor que el valor máximo (7,7). En este caso, si empezamos con el 1 y acabamos en el 8, con siete intervalos de longitud 1 cubriremos todo el recorrido: Intervalo Marca de clase, xi [1,2[ [2,3[ [3,4[ [4,5[ [5,6[ [6,7[ [7,8[ Total ni 49 Ni fi Fi 1 Ejercicios: 1º) Se ha realizado un estudio sobre la edad de los asistentes al teatro. Esta tabla muestra los resultados. Completa la tabla de frecuencias. ¿Qué porcentaje de los asistentes tiene entre 30 y 40 años?¿Qué porcentaje tiene menos de 40 años? Edad Nº personas [20,30[ 19 [30,40[ 36 [40,50[ 41 [50,60[ 29 1.3. Gráficos estadísticos La información de las tablas de frecuencias también se puede representar mediante gráficos estadísticos. Diagrama de barras – Ejemplo1 Polígono de frecuencias – Ejemplo1 En el eje de abscisas se escriben los datos de la variable con la misma separación (aunque sean datos numéricos no equidistantes), y en el eje de ordenadas las frecuencias. Sobre cada valor se levanta un rectángulo cuya altura es igual a la frecuencia. En el eje de abscisas se escriben los datos de la variable con la misma separación (aunque sean datos numéricos no equidistantes), y en el eje de ordenadas las frecuencias. Sobre cada valor se marca un punto cuya altura es igual a la frecuencia y se unen formando una poligonal. 3/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I ESTADÍSTICA Histograma – Ejemplo2 (para intervalos) Diagrama de sectores – Ejemplo1 En el eje de abscisas se representan los intervalos de clase y en el eje de ordenadas las frecuencias. Sobre cada intervalo se levanta un rectángulo de altura igual a su frecuencia. Si se traza la poligonal que une los puntos medios de las bases superiores de los rectángulos se puede obtener también el polígono de frecuencias. En el caso, poco frecuente, de que los intervalos no tengan la misma amplitud, los rectángulos que se levantan deben tener el área proporcional a las frecuencias. Se divide un círculo en tantos sectores como datos tenga la variable, y la amplitud de cada uno debe ser proporcional a las frecuencias que toma la variable. Se suele acompañar por el tanto por ciento que representa cada sector, f i ⋅ 100 . Se trata de repartir los 360º del proporcionalmente a las frecuencias: f i ⋅ 360 . círculo Hay otros gráficos estadísticos como: Pictogramas: Diagrama de barras con dibujos representativos de la variable, en lugar de rectángulos. Cartogramas: Mapas coloreados según los valores de la variable. Diagrama de barras horizontal: Diagrama de barras con la posición de los ejes invertida. Pirámide de población: Dos histogramas horizontales que comparten los intervalos de clase en el eje vertical. 1.4. Parámetros de centralización Una vez ordenados los datos en las tablas de frecuencias, la información se suelde sintetizar con unas medidas llamadas parámetros estadísticos. Los hay de dos tipos: de centralización y de dispersión. Los parámetros de centralización nos indican en torno a qué valor (centro) se distribuyen los datos, y son la media, la moda y la mediana. La media aritmética: es el valor que se obtiene al dividir la suma de todos los datos entre el número total de éstos. En lugar de sumar los N datos es más cómodo multiplicar cada xi por su frecuencia absoluta ni . La media se representa por: x x i ni . N Si los datos están agrupados por intervalos se toman como xi las marcas de clase. La moda , Mo, es el valor de la variable con mayor frecuencia absoluta. Puede haber variables con más de una moda. Si los datos están agrupados por intervalos se puede tomar como moda la marca de clase del intervalo con mayor frecuencia, aunque tiene más sentido hablar del intervalo modal. 4/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I ESTADÍSTICA La mediana, Me, es el valor que ocupa la posición central, una vez ordenados todos los datos. Si el nº de datos es par hay dos datos centrales y tomaremos como mediana el promedio (media) de los dos. Si los datos están agrupados por intervalos se habla de intervalo mediano, y es el primero cuya frecuencia absoluta acumulada, Ni, es mayor o igual que la mitad del nº de datos, N/2. Ejemplo3: 0 1 2 3 Se pregunta a una serie de personas cuántos cafés toman Nº de cafés al día y obtenemos los siguientes datos: Nº de personas 2 4 3 1 2 ⋅ 0 + 4 ⋅1 + 3 ⋅ 2 + 1 ⋅ 3 La media es x = = 1,3 cafés. 10 La mayor frecuencia es 4, que corresponde a 1 café: Mo=1 café, es la moda. Ordenamos los datos: 0, 0, 1, 1, 1, 1, 2, 2, 2, 3; como N=10 es par hay dos datos centrales, los que 1+1 ocupan el 5º y el 6º lugar, luego la mediana es la media de esos dos datos: Me = = 1. 2 − La media indica que, por término medio, el nº de cafés diarios es 1,3. Es decir entre 1 y 2 cafés (aunque más veces 1 que 2). − La moda señala que lo más frecuente es tomarse un café al día. − La mediana indica que hay tanta gente que toma un café o más como gente que toma un café o menos. Ejercicios: 2º) Los siguientes datos corresponden a los precios de 25 discos que están en oferta: 10, 8, 12, 9, 11, 11, 11, 12, 9, 10, 11, 12, 11, 10, 8, 11, 10, 10, 9, 10, 11, 11, 12, 9, 15. Calcula los parámetros de centralización. 3º) a) Completa los datos que faltan en la siguiente tabla estadística, xi ni Ni fi donde ni , N i y f i representan, respectivamente, la frecuencia 1 4 0,08 absoluta, acumulada y relativa. b) Calcula la media, mediana y moda de esta distribución. 2 3 4 5 6 7 8 4 16 7 5 7 0,16 0,14 28 38 45 1.5. Parámetros de dispersión Los parámetros de dispersión informan sobre cuánto se alejan del centro los valores de la variable, es decir, permiten conocer el grado de agrupamiento de los datos en torno a las medidas de centralización. Los más comunes son el recorrido, la varianza y la desviación típica. Recorrido: es la diferencia entre el mayor y el menor valor de la variable. En el ejemplo3 el recorrido es 3. Nos da una idea de la amplitud del conjunto de datos. Varianza: es la media de los cuadrados de las desviaciones de los datos respecto de ( x i − x ) 2 ⋅ ni ∑ 2 la media. Se representa por = . Hay otra fórmula equivalente N x i2 ni 2 x2 . para calcular la varianza y de cálculo un poco más sencillo: N Desviación típica: es la raíz cuadrada de la varianza. Se representa con σ. 5/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I ESTADÍSTICA Coeficiente de variación: es el cociente entre la desviación típica y la media: CV = . Se puede expresar en forma de porcentaje y se utiliza para comparar la x dispersión de dos conjuntos de datos de la misma variable que no tienen la misma media. Si la media es el centro de gravedad de la distribución, la desviación típica nos dice cómo de dispersos están los datos. Si observamos las siguientes distribuciones, todas tienen la misma media, pero sus desviaciones típicas son diferentes: En la primera todos los valores están acumulados en la media. Su desviación típica es 0, ya que no hay dispersión. Al pasar de cada una a la siguiente aumenta la dispersión, pues cada vez más individuos se van alejando de la media. Ejemplo4: Queremos comparar la duración de dos marcas de lentes desechables, A y B. Para ello observamos la duración en horas de 10 pares de lentes de cada marca y obtenemos los resultados de la siguiente tabla. ¿Qué marca es aconsejable escoger? A 144 142 140 141 145 144 139 141 142 144 B 143 143 148 136 142 150 134 142 134 150 Organizamos los datos en tablas para calcular la media y la desviación típica de cada una de las dos distribuciones. A B 2 2 2 xi ni x i ⋅ ni xi ni x i ⋅ ni x i ⋅ ni xi2 ⋅ ni xi xi ∑ La media es: x = 2 x ∑ N= 2 i ni ∑x ⋅n i N i N= La media es: x = = x = x 2 i ∑x ⋅n i N i = ni x2 = N La desviación típica es: 2 N La desviación típica es: 6/13 2 IBR-IES LA NÍA MATEMÁTICAS CC SS I ESTADÍSTICA Las dos tienen la misma duración media. Es aconsejables escoger la marca A pues la DT es mucho menor: 1,89 frente a 5,74. Esto indica que, por lo general, la duración de estas lentillas se aleja poco de la media. Ejemplo5: Dos grupos de 1º de bachillerato, B y C, han hecho el mismo examen. Los parámetros obtenidos son xB = 6,5, B = 2,08, xC = 8,5, C = 2,38 . Si las medias fueran iguales, como en el ejemplo anterior, estaría claro que las notas de 1ºC serían más dispersas porque C > B . Como las medias son distintas, para comparar la dispersión, utilizamos el coeficiente de variación: 2,08 2,38 CVB = = = 0,32 y CVC = = 0,28 x 6,5 8,5 Ejercicios: 4º) El nº de aciertos de 100 alumnos en una prueba de 30 pregunta se representa en la siguiente tabla. Calcula todos los parámetros de centralización y dispersión. Aciertos [0,5[ [5,10[ [10,15[ [15,20[ [20,25[ [25,30[ Alumnos 3 10 25 38 16 8 1.6. Medidas de posición Sabemos que la mediana es el valor que ocupa la posición central en un conjunto ordenado de valores (o el promedio de los valores centrales si el nº de datos es par): Si generalizamos este concepto, podemos considerar los valores que dividen la distribución en cuatro partes iguales: los cuartiles. Hay tres cuartiles, Q1, Q2 y Q3, que son los valores de la variable que dividen el conjunto ordenado de datos en cuatro partes iguales. En el caso de distribuciones discretas obtenemos primero la mediana, Q2 , en la forma ya explicada. Para obtener el primer cuartil, Q1 ¸ hacemos otra mediana con los datos anteriores a Q2 . Para el tercer cuartil, Q3 ¸ hacemos otra mediana más, pero ahora con los datos posteriores a Q2 . Ejemplo6: Estudiamos el nº de horas semanales que cada uno de los 25 alumnos de un grupo ha faltado a clase: Primero calculamos la mediana, Q2 : como N=25 es impar hay un valor central, que ocupará la posición nº 13 → Me= Q2 =2. De los doce valores anteriores a la mediana, los valores centrales serían dos, la sexta y la séptima posiciones, luego se haría el promedio de ambos valores, pero como ambos son 0 → Q1 =0. 7/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I ESTADÍSTICA El tercer cuartil estaría entre las posiciones 19 y 20, por tanto hacemos el promedio de los 6 + 10 dos valores que ocupan esas posiciones → Q3 = =8. 2 Para obtener los cuartiles en el caso de datos agrupados se analizan las frecuencias acumuladas. Buscamos primero el intervalo que contiene al cuartil: el primer valor que tiene una frecuencia absoluta acumulada mayor que N 4 para Q1 , el primer valor que tiene una frecuencia absoluta acumulada mayor que N 2 para Q2 (mediana) y el primer valor que tiene una frecuencia absoluta acumulada mayor que 3N 4 para Q3 . Una vez determinados los intervalos utilizamos las siguientes fórmulas: N N 3N − N i −1 − N i −1 − N i −1 Q1 = Li + a ⋅ 4 , Q2 = Li + a ⋅ 2 y Q3 = Li + a ⋅ 4 , donde ni ni ni Li es el extremo inferior del intervalo I que contiene al cuartil a es la amplitud de los intervalos N el nº de datos Ni-1 es la frecuencia absoluta acumulada del intervalo anterior a I ni es la frecuencia absoluta del intervalo I. Estas fórmulas se obtienen por interpolación lineal, suponiendo que los datos de cada intervalo se reparten uniformemente en él, y que es al final de cada intervalo cuando se alcanza la frecuencia acumulada correspondiente: El recorrido intercuartílico es la diferencia entre el tercer y el primer cuartil: Q3 − Q1 . En el recorrido intercuartílico figura el 50% de los datos; por tanto, cuanto menor sea este recorrido, más concentrados estarán. Cuando un conjunto de datos está muy disperso, no es conveniente representarlos con la media aritmética y, por tanto, tampoco tiene sentido calcular la desviación típica, ya que es un parámetro de dispersión que depende de la media. En estos casos, el parámetro central que se debe hallar es la mediana, y los parámetros de dispersión son el recorrido y el recorrido intercuartílico. De la misma manera, podemos dividir la distribución en 100 partes iguales y considerar los valores que dejan por debajo un porcentaje (k%) determinado de datos. Estos valores se llaman percentiles y se representan Pk. Para calcularlos se procede como en el caso de los cuartiles: k⋅N buscamos el primer intervalo con frecuencia absoluta acumulada mayor que el k% de N: ,y 100 kN − N i −1 100 sustituimos en: Pk = Li + a ⋅ ni Ejercicios: 5º) Con los datos del Ejemplo1 calcula la media, la moda, la mediana, la desviación típica, el coeficiente de variación, los cuartiles, el recorrido, el recorrido intercuartílico y el percentil 32. 8/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I ESTADÍSTICA 6º) Halla los cuartiles, el recorrido intercuartílico y el percentil 95 en la distribución de las estaturas representadas en Estatura 148,5-153,5 153,5-158,5 158,5-163,5 163,5-168,5 168,5-173,5 173,5-178,5 ni 2 4 11 14 5 4 Intervalo ni 7º) En la siguiente tabla aparece el peso (en gr) de 100 comprimidos de un [4,45 , 4,55) 1 medicamento. [4,55 , 4,65) 2 a) Construye el histograma y el polígono de frecuencias. [4,65 , 4,75) 10 b) Calcula la media y la desviación típica. [4,75 , 4,85) 21 c) Calcula el primer y tercer cuartiles y el percentil 15. [4,85 , 4,95) 33 d) ¿Qué porcentaje de comprimidos pesa menos de 4,87 gr? [4,95 , 5,05) [5,05 , 5,15) [5,15 , 5,25) [5,25 , 5,35) 18 9 4 2 2. VARIABLES ESTADÍSTICAS BIDIMENSIONALES Si al efectuar un estudio estadístico se consideran conjuntamente dos características diferentes de los individuos de una misma población, X e Y, resulta una variable estadística bidimensional (X,Y). Ejemplos: − Estudio de la altura y el peso de un colectivo. − Calificación de dos asignaturas de un curso. − Capital invertido en publicidad y ventas obtenidas posteriormente. − Número de leucocitos y plaquetas en la sangre de personas afectadas por una cierta enfermedad. 2.1. ORGANIZACIÓN DE DATOS Para organizar los datos de una variable estadística bidimensional se utilizan las tablas de doble entrada, en las cuales se agrupan los datos en filas y columnas. Construimos una tabla con tantas columnas como valores tome X y con tantas filas como valores tome Y en la distribución. Hallamos la frecuencia absoluta de cada par de valores de la variable (X, Y). Para ello contamos el número de veces que se repite ese par de valores en la distribución y lo anotamos en la casilla correspondiente (frecuencia absoluta conjunta). Después añadimos la última fila y la última columna de la tabla de doble entrada que contienen, respectivamente, las frecuencias absolutas de las variables X e Y, consideradas por separado. Estas frecuencias reciben el nombre de frecuencias marginales. Ejemplo7: Preguntamos a algunas personas sobre el nº de autobuses (X) que utilizan y el tiempo (Y), en minutos, que tardan en llegar a su destino. Mostramos los resultados en una tabla de doble entrada: 9/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I ESTADÍSTICA • 16 es la frecuencia absoluta conjunta del par (2,20), es decir, hay 16 personas que utilizan dos autobuses y tardan veinte minutos en llegar a su destino. • Si sumamos toda la columna de X=2 obtenemos 30, que es la frecuencia absoluta marginal de ese resultado para la variable unidimensional X. Significa que hay 30 personas que cogen 2 autobuses. • Si sumamos toda la fila de y=20 obtenemos 27, que es la frecuencia absoluta marginal de ese resultado para la variable unidimensional Y. Significa que hay 27 personas que tardan 20 minutos en llegar. Distribución Distribución marginal de marginal de X Y Si consideramos por separado los datos de la última columna y de la xi ni yi ni última fila se obtienen las distribuciones marginales: 1 45 10 17 2 30 20 27 3 15 30 22 También se puede hacer una tabla de la distribución bidimensional 90 40 16 Σ con todos los pares de resultados y sus frecuencias absolutas: 50 8 90 Σ xi 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 yi 10 20 30 40 50 10 20 30 40 50 10 20 30 40 50 ni 12 8 14 7 4 4 16 3 5 2 1 3 5 4 2 Ejercicio: 8º) Los datos obtenidos al estudiar las variables X = número de goles marcados e Y = número de goles recibidos, en 40 partidos jugados \ por el equipo campeón de la liga de fútbol sala, son: (5, 4), (4, 2), (6, 3), (4, 4), (3, 2), (6, 4), (3, 1), (4, 2), (4, 2), (6, 4), (4, 2), (5, 3), (3, 1), (2, 2), (4, 3), (3, 1), (4, 2), (5, 3), (5, 3), (4, 2), (3, 3), (1,1), (4, 2), (5, 3), (3, 2), (5, 3), (6, 4), (4, 2), (5, 3), (2, 1), (3, 2), (6, 4), (5, 3), (4, 2), (4, 2), (3, 3), (3, 1), (2, 2), (6, 4), (5, 3) Construye la tabla de doble entrada, las distribuciones marginales y la tabla de la distribución bidimensional con las frecuencias de todos los pares de resultados. 2.2. Relación entre variables- Diagrama de dispersión Se llama diagrama de dispersión o nube de puntos al gráfico que se obtiene al representar en unos ejes de coordenadas todos los pares correspondiente a los datos observados. • Si los puntos se ajustan completamente a una recta o a una curva cuya expresión matemática podríamos determinar, hay una dependencia funcional entre las dos variables. • Si los puntos de la nube se agrupan en torno a una posible curva o recta , no muy definida, pero reconocible, diremos que hay dependencia estadística o correlación entre las dos variables 10/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I • ESTADÍSTICA Si los puntos de la nube no se agrupan en torno a ninguna curva y están completamente dispersos, diremos que las dos variables son independientes. Nosotros vamos a estudiar la dependencia o correlación lineal, es decir, si los puntos siguen aproximadamente una configuración rectilínea. − Diremos que la correlación o dependencia es positiva si la recta a la que se ajustan los puntos es creciente, y que es negativa si la recta a la que se ajustan los puntos es decreciente. − Diremos que la correlación o dependencia es fuerte si la nube de puntos está muy próxima a la recta (la nube es estrecha), y que es débil si la nube de puntos se ajusta menos a la recta (la nube es más ancha). 2.3. Covarianza y coeficiente de correlación Cada una de las variables estadísticas que forman la distribución bidimensional puede ser analizada independientemente, y podemos calcular su media y su desviación típica: x , x , y , y . El punto ( x , y ) es el punto medio de la distribución bidimensional, es decir, si se sujetara la nube de puntos apoyándola en él, el diagrama estaría en equilibrio. Introducimos un nuevo parámetro estadístico que mide la desviación de cada variable respecto de ∑( xi − x )( y i − y )ni ∑ xi y i ni su media, la covarianza: XY = = − xy . N N Par cuantificar la correlación lineal entre dos variables se calcula el coeficiente de correlación de Pearson: r = XY X ⋅ Y El coeficiente de correlación indica la aproximación de los valores de la variable a una línea recta: − Si r >0 la correlación es positiva; si r <0 la correlación es negativa. − Su valor está comprendido entre -1 y 1. − Cuanto más se acerque a 0 la dependencia es más débil. − Cuanto más se acerque a -1 o 1 la dependencia es más fuerte. (si llega a -1 o a 1 es dependencia funcional) 11/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I ESTADÍSTICA Ejercicios: 9º) Se han observado dos variables conjuntas en 50 individuos. La información obtenida se ha resumido en la siguiente tabla incompleta: a) Completa la tabla. b) Obtén la covarianza. c) Calcula el coeficiente de correlación e interprétalo. 10º) El número de horas dedicadas al estudio de una asignatura y la calificación final obtenida en el correspondiente Horas de 20 16 34 23 27 32 18 22 examen por ocho personas vienen dados en la estudio:X siguiente tabla. Halla la covarianza y el coeficiente Calificación: 6,5 6 8,5 7 9 9,5 7,5 8 de correlación entre las dos variables. Interpreta el Y significado del coeficiente de correlación. 2.4. Rectas de regresión. Estimación Llamaremos recta de regresión a la que mejor se ajuste a la nube de puntos. La regresión pretende explicar el comportamiento de una variable según los valores que toma la otra. Si deseamos saber el valor de la variable Y según los valores que toma X, la regresión se llama de Y sobre X. La recta de regresión de Y sobre X debe hacer mínima la suma de las distancias entre las ordenadas de cada punto y la recta, y su ecuación es: y−y = xy (x − x) x2 Si deseamos saber el valor de la variable X según los valores que toma Y, la regresión se llama de X sobre Y. La recta de regresión de X sobre Y debe hacer mínima la suma de las distancias entre las abscisas de cada punto y la recta, y su ecuación es: x − x = xy ( y − y) y2 Las dos rectas de regresión tienen un punto en común, ( x , y ) , luego se cortan en ese punto. Además, cuanto más fuerte sea la dependencia (r más cerca de -1 o 1), menor será el ángulo que forman las rectas: Las rectas de regresión nos permiten obtener de forma aproximada el valor esperado de una variable, conocida la otra. El valor obtenido es una estimación, y es más fiable si r toma valores próximos a -1 o 1. Además la estimación debe hacerse para valores dentro del intervalo de datos o muy próximos a él. Ejercicios: 11º) El índice de mortalidad, Y, de una muestra de población que consumía diariamente X cigarrillos aparece en la siguiente tabla, donde se estudiaron siete muestras distintas de población que consumía distinto nº de cigarrillos. Estudia la correlación entre X e Y. 12/13 IBR-IES LA NÍA MATEMÁTICAS CC SS I nº cigarrillos Índice mortalidad ESTADÍSTICA 3 0,2 5 0,3 6 0,3 15 0,5 20 0,7 40 1,4 45 1,5 ¿Qué mortalidad se podría predecir para un consumidor de 60 cigarrillos diarios? 12º) La siguiente tabla muestra los valores de las variables (X,Y), X: gastos en publicidad de un producto (miles de €), Y: ventas conseguidas (miles de €) x 1 2 3 4 5 6 y 10 17 30 28 39 47 Halla las dos rectas de regresión y calcula la estimación de Y para x=5,5, y la estimación de X para y=15, y explica su significado. 13º) Una persona se somete a una dieta de adelgazamiento. La siguiente tabla muestra el peso en kilogramos de esta persona, Y, según el nº de semanas, X, que lleva haciendo dieta: Calcula e interpreta el coeficiente de correlación. X 1 2 3 4 5 6 Y 92 88 85 83 80 77 ¿Cuánto cabe esperar que pese esta persona después de 8 semanas de dieta? ¿Cuánto pesaría si siguiese esta dieta 20 semanas? Valora los resultados. 14º) La siguiente tabla recoge las notas en Matemáticas, X, y las notas medias de todas las asignaturas, Y, de 10 alumnos. .X 4 6 8 5 6 3 5 6 8 3 Y 5 7 8 6 6 4 6 7 8 4i — ¿qué nota media se podría estimar? a) Si un alumno obtiene un 7 en Matemáticas, —j¿qué nota tendría en Matemáticas? b) Si un alumno tuviera un 3 de nota media c) ¿Son fiables ambas estimaciones? Razona la respuesta. [ x = 5,4; y = 6,1; x = 1,69; y = 1,37; xy = 2,26 ; y = 0,8 x + 1,78 ; x = 1,2 y − 1,92 ; a)7,38; b)1,68; r=0,98] 15º) Se ha realizado un estudio estadístico a un grupo de 100 alumnos. Con los datos recogidos se ha obtenido que la estatura media del grupo es de 155 cm, con una desviación típica de 15,5 cm. La recta de regresión que relaciona el peso de los alumnos, X, con su estatura, Y, es y = 80 + 1,5 x a) ¿Cuál es el peso medio del grupo de alumnos? b) ¿Cuál será el signo de la covarianza? c) ¿Se puede afirmar, en este grupo de alumnos, que cuanto mayor sea el peso hay mayor altura? 16º) Indica cuál es la correlación correspondiente a cada una de las nubes de puntos y explica por qué. 1) r=0,95 2) r=-1 3) r=0 4) r=-0,63 17º) Asocia razonadamente las siguientes rectas de regresión con las nubes de puntos de las 1 figuras: 1) y=-2x+10 2) y=x+4 3) y = x + 2 3 13/13 IBR-IES LA NÍA