File
Anuncio

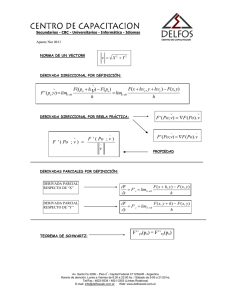
El Cálculo Diferencial: Definiciones web: El Cálculo Diferencial, es una parte importante del análisis matemático y dentro del mismo del cálculo infinitesimal. Hace parte de las matemáticas avanzadas. El cálculo diferencial es una parte importante del análisis matemático y dentro del mismo del cálculo infinitesimal. Consiste en el estudio del cambio de las variables dependientes cuando cambian las variables independientes de las funciones o campos objetos del análisis. El principal objeto de estudio en el cálculo diferencial es la derivada. Una noción estrechamente relacionada es la de diferencial de una función. En el estudio del cambio de una función, es decir, cuando cambian sus variables independientes es de especial interés para el cálculo diferencial el caso en el que el cambio de las variables es infinitesimal, esto es, cuando dicho cambio tiende a cero (se hace tan pequeño como se desee). Pues el cálculo diferencial se apoya constantemente en el concepto básico del límite. El paso al límite es la principal herramienta que permite desarrollar la teoría del cálculo diferencial y la que lo diferencia claramente del álgebra. Desde el punto de vista matemático de las funciones y la geometría, la derivada de una función en un cierto punto es una medida de la tasa en la cual una función cambia conforme un argumento se modifica. Esto es, una derivada involucra, en términos matemáticos, una tasa de cambio. Una derivada es el cálculo de las pendientes instantáneas de f(x) en cada punto . Esto se corresponde a las pendientes de las tangentes de la gráfica de dicha función en sus puntos (una tangente por punto); Las derivadas pueden ser utilizadas para conocer la concavidad de una función, sus intervalos de crecimiento, sus máximos y mínimos. Recordemos que La inversa de una derivada se llama primitiva, antiderivada indefinida, temas a tratar en Calculo Integral. o integral Diferenciación y diferenciabilidad La Diferenciación puede ser usada para determinar el cambio que se produce como resultado de otro cambio, si está determinada una relación matemática entre dos objetos. Una función es diferenciable en un punto si: Su derivada existe en ese punto; una función es diferenciable en un intervalo. Si lo es en cada punto perteneciente al intervalo. Si una función no es continua en a, entonces no puede ser diferenciable en a; sin embargo, aunque una función sea continua en a, puede no ser diferenciable. Es decir, toda función diferenciable en un punto a es continua en a, pero no toda función continua en a es diferenciable en a (como f(x) = |x| es continua pero no diferenciable en x = 0). Definición de Derivada Las derivadas se definen tomando el límite de la pendiente de las rectas secantes conforme se van aproximando a la recta tangente. Es difícil hallar directamente la pendiente de la recta tangente de una función porque sólo conocemos un punto de ésta, el punto donde ha de ser tangente a la función. Por ello, aproximaremos la recta tangente por rectas secantes. Cuando tomemos el límite de las pendientes de las secantes próximas, obtendremos la pendiente de la recta tangente. Para obtener estas pendientes, tomemos un número arbitrariamente pequeño que llamaremos h. h representa una pequeña variación en x, y puede ser tanto positivo como negativo. La pendiente de la recta entre los puntos x, f(x) y x h, f(x h) es f ( x h) f ( x) h Esta expresión es un Cociente Diferencial de Newton. La derivada de f en x es el límite del valor del cociente diferencial conforme las líneas secantes se acercan más a la tangente: Si la derivada de f existe en cada punto x, podemos definir la derivada de f como la función cuyo valor en el punto x es la derivada de f en x. Para comprender mejor este tema observe, lea y estudie detenidamente los siguientes ejemplos de cómo utilizar este cociente: Ejemplo 1 Consideremos la siguiente función: Entonces: Esta función es constante, para cualquier punto de su dominio vale 5 (por eso f(x+h)=5). Nótese el último paso, donde h tiende a cero pero nunca lo alcanza. Si pensamos un poco, observaremos que la derivada además de ser la pendiente de la recta tangente a la curva, es a la vez, la recta secante a la misma curva. Ejemplo 2 Consideremos la función f ( x ) 2 x 3 . Su grafica es una recta y tiene una pendiente igual a 2.0 en cada punto. Utilizando el cociente mostrado arriba (junto a los conceptos de límite, secante y tangente) podremos determinar las pendientes en los puntos 4 y 5: Entonces: Y vemos que se cumple para cualquier número n: Por tanto, se deduce que el valor de la función derivada de una recta es igual a la pendiente de la misma. Ejemplo 3 Mediante esta diferenciación, se puede calcular la pendiente de una curva. Consideremos que: f ( x ) x2 Entonces: 2 Para cualquier punto x, la pendiente de la función f ( x ) x es f ( x ) 2 x . El Cociente Diferencial Alternativo La derivada de f(x) (tal como la definió Newton) se describió como el límite, conforme h se aproxima a cero. Una explicación alternativa de la derivada puede ser interpretada a partir del cociente de Newton. Si se utiliza la fórmula anterior, la derivada en c es igual al límite conforme h se aproxima a cero de f ( c h ) f ( c ) h . Si se deja que h = x – c (por ende c + h = x), entonces x se aproxima a c (conforme h tiende a cero). Así, la derivada es igual al límite conforme x se aproxima a c, de f ( x ) f ( c ) x c Esta definición se utiliza para una demostración parcial de la regla de la cadena. Notaciones para la diferenciación La derivada de una función puede a su vez ser diferenciable, hablándose entonces de segunda derivada de la función como la derivada de la derivada de ésta. Análogamente, la derivada de la segunda derivada recibe el nombre de tercera derivada, y así sucesivamente. A partir de la f ( a ) segunda derivada: hasta la enésima derivada: f n( a ) reciben el nombre de Derivada de Orden Superior. La notación más simple para la diferenciación que se utiliza en la actualidad se debe a Lagrange y utiliza un apóstrofo o comilla: ′. De esta manera se expresan las derivadas de la función en el punto f(x) , se escribe: Para la primera derivada, Para la segunda derivada, Para la tercera derivada, y luego de forma general, Para la n-ésima derivada (donde normalmente se da que n > 3). Para la función cuyo valor en cada similar, para la segunda derivada de es la derivada de f se escribe f ( x ), se escribe f ( x ) f ( a ) , y así sucesivamente. . De forma La otra notación común para la diferenciación se debe a Leibniz. Para la función cuyo valor en es la derivada de f en , se escribe: d ( f ( x )) dx Se puede escribir la derivada de f en el punto a de dos formas distintas: Si la resultante de f(x) es otra variable, por ejemplo, si y=f(x), se puede escribir la derivada como: dy dx Las derivadas de orden superior se expresan así o Para la n-ésima derivada de f(x) o y respectivamente. Históricamente, esto proviene del hecho de que, por ejemplo, la tercera derivada es: que se puede escribir sin mucho rigor como: Eliminando las llaves nos da la notación que está arriba. La notación de Leibniz es tan versátil que permite especificar la variable que se utilizará para la diferenciación (en el denominador). Esto es específicamente relevante para la diferenciación parcial. Y también hace más fácil de recordar la reglad e la cadena, debido a que los términos "d" se cancelan simbólicamente: . Sin embargo, es importante recordar que los términos "d" no se pueden cancelar literalmente, debido a que son un operador diferencial. Sólo se utilizan cuando se usan en conjunto para expresar una derivada. La notación de Newton para la diferenciación consiste en poner un punto sobre el nombre de la función: y así sucesivamente. La notación de Newton se utiliza principalmente en la mecánica, normalmente para las derivadas con respecto al tiempo tales como la velocidad y la aceleración y en la teoría de ecuaciones diferenciales ordinarias. Normalmente sólo se utilizan para la primera y segunda derivadas. Otra notación consiste en colocar una letra 'D' mayúscula para indicar la operación de diferenciación con un subíndice que indica la variable sobre la que se derivará: equivalente a la expresión: d f. dx Dx f , que es En ese contexto se considera a la diferenciación como una operación sobre funciones, de modo que los símbolos d dx y Dx son llamados operadores diferenciales. Aplicaciones importantes del cálculo diferencial Recta tangente a una función en un punto: La recta tangente a una función f es como se ha visto el límite de las rectas secantes cuando uno de los puntos de corte de la secante con la función se hace tender hacia el otro punto de corte. También puede definirse a la recta tangente como la mejor aproximación lineal a la función en su punto de tangencia, esto es, la recta tangente es la función polinómica de primer grado que mejor aproxima a la función localmente en el punto de tangencia que consideremos. Uso de las derivadas para realizar gráficos de funciones: Las derivadas son una útil herramienta para examinar las gráficas de funciones. En particular, los puntos en el interior de un dominio de una función de valores reales que llevan a dicha función a un extremo local tendrán una primera derivada de cero. Sin embargo, no todos los puntos críticos son extremos locales. Por ejemplo, f(x)=x³ tiene un punto crítico en x=0, pero en ese punto no hay un máximo ni un mínimo. La prueba de la primera derivada y la prueba de la segunda derivada permiten determinar si los puntos críticos son máximos, mínimos o ninguno. En el caso de dominios multidimensionales, la función tendrá una derivada parcial de cero con respecto a cada dimensión en un extremo local. En este caso, la prueba de la segunda derivada se puede seguir utilizando para caracterizar a los puntos críticos, considerando el eigenvalor de la matriz Hessiana de las segundas derivadas parciales de la función en el punto crítico. Si todos los eigenvalores son positivos, entonces el punto es un mínimo local; si todos son negativos es un máximo local. Si hay algunos eigenvalores positivos y algunos negativos, entonces el punto crítico es un punto silla, y si no se cumple ninguno de estos casos, la prueba es no concluyente. Una vez que se encuentran los extremos locales, es mucho más fácil hacerse de una burda idea de la gráfica general de la función, ya que (en el caso del dominio mono dimensional) se incrementará o decrementará uniformemente excepto en los puntos críticos, y por ello (suponiendo su continuidad) tendrá valores intermedios entre los valores en los puntos críticos de cada lado. Aproximación local de Taylor: Hemos visto que podemos aproximar mediante su recta tangente a una función derivable localmente en un punto. Si se cumple que la función es suficientemente suave en el punto o dominio de estudio (esto es, la función es de clase C ) cabe la posibilidad de intentar aproximar a la función no por polinomios de grado uno, sino por polinomios de grado dos, tres, cuatro y sucesivamente. Esta aproximación recibe el nombre de "desarrollo polinómico de Taylor" y se define de la siguiente manera: P( x ) f(a) f (a) f ( a ) f ( a ) f n( a ) ( x a ) ( x a )2 ( x a )3 ( x a )n 1! 2! 3! n! Donde P(x) es el polinomio de grado n que mejor aproxima a la función en el punto x=a. Nótese que si evaluamos P(x) en x = a todos los términos salvo el f(a) se anulan, luego P(a) = f(a). Nótese también que la ecuación de la recta tangente del apartado anterior corresponde al caso en el que n=1. El polinomio de Taylor es un polinomio "osculador". De entre todos los polinomios de orden no mayor que "n" y que pasan por f(a) el desarrollo polinómico de Taylor de f(x) en x=a es el que posee el contacto de mayor orden con f(x) en "a". Se basa en la idea de que si dos funciones comparten en x=a el mismo valor, la misma primera derivada, la misma segunda derivada etc, la misma i-ésima derivada, (lo que brevemente se expresa diciendo que las dos funciones tienen un contacto de orden "i") entonces dichas funciones serán muy parecidas cerca de x=a, queriendo decir por parecidas que podemos aproximar a una de las dos por la otra cometiendo un error despreciable. Cuando a=0 el desarrollo se denomina "desarrollo de MacLaurin". En la práctica la mayoría de las veces se emplean desarrollos de MacLaurin. Ejemplos de desarrollos importantes de MacLaurin son: Nótese el símbolo que denota aproximación que no igualdad. Si la función a aproximar es infinitamente derivable y agregamos infinitos términos al desarrollo entonces el un se convierte en . Este último paso de agregar infinitos términos no se puede tomar a la ligera. Hemos dicho que la aproximación de grado uno, dos, tres y así sucesivamente, es una aproximación local en el punto en que se evalúa la función, esto es, si nos alejamos mucho del punto la aproximación dejará de ser precisa. Cuantos más términos agreguemos al desarrollo en serie de Taylor tanto más precisa será nuestra aproximación si estamos en un entorno del punto. Podríamos pensar pues que al añadir infinitos términos podemos evaluar la función aproximada en cualquier punto de su dominio de definición con precisión absoluta. Esto no siempre es cierto, pues dependerá del carácter de la serie de Taylor en el punto en que la evaluamos. El estudio del carácter de una serie es un problema frecuentemente complejo. Se trata de definir los valores para los cuales la serie es convergente, esto es, determinar el radio de convergencia de la misma. Dentro del intervalo de convergencia de la serie sí que podemos tomar infinitos términos y admitir que la serie nos da el valor "exacto" de la función en el punto. Sin embargo, fuera del intervalo de convergencia la serie no proporcionará el valor exacto de la función aunque agreguemos infinitos términos. Los desarrollos en serie de Taylor presentan grandes ventajas a la hora de operar funciones cuyas ecuaciones involucran expresiones complicadas tales como funciones trascendentes (senos, logaritmos, entre otros). Sin embargo también presentan ciertos inconvenientes. Un inconveniente importante es que el número de términos necesarios para aproximar con precisión razonable a la función en un punto alejado del evaluado (pero siempre dentro del intervalo de convergencia de la serie) se dispara al infinito. Otro inconveniente es que la expresión polinómica de la función puede hacer difícil detectar sus propiedades elementales, por ejemplo, no es obvio deducir del desarrollo del seno que se trata de una función periódica. Los desarrollos en serie son una potente herramienta en el cálculo de límites. Un límite aparentemente complejo puede convertirse en trivial sin más que sustituir cada función por su desarrollo en serie y realizar las operaciones correspondientes de simplificación. Puntos singulares: Se denominan puntos singulares ó estacionarios a los valores de la variable en los que se anula la derivada f ( x ) de una función f(x), es decir, si f ( x ) 0 en x1, x2, x3,, xn , entonces x1, x2, x3,, xn son puntos singulares de f(x). Los valores f(x1), f(x2), f(x3), . . . , f(xn), se llaman valores singulares. Puntos críticos: Por punto crítico se entiende: un punto singular, un punto donde no exista la derivada o un punto extremo a o b del dominio [a,b] de definición de la función. Si la segunda derivada es positiva en un punto crítico, se dice que el punto es un mínimo local; si es negativa, se dice que el punto es un máximo local; si vale cero, puede ser tanto un mínimo, como un máximo o un punto de inflexión. Derivar y resolver en los puntos críticos es a menudo una forma simple de encontrar máximos y mínimos locales, que pueden ser empleados en optimización. Aunque nunca hay que despreciar los extremos en dichos problemas Teoremas para el cálculo de la derivada La definición de la derivada en términos de límites se emplea para demostrar las reglas de diferenciación. Dichas reglas sirven para calcular la derivada de una función a través de una manipulación algebraica en vez de recurrir a la aplicación directa del cociente diferencial de Newton. Regla de la constante: La derivada de cualquier contante es cero. Regla de la multiplicación por una constante: Si c es cualquier número real, entonces la derivada de cf ( x ), es igual a c multiplicado por la derivada de f(x). Esto es una consecuencia de la linealidad, que se verá más adelante. Lineadlidad: af ( x ) bg( x ) af ( x ) bg ( x ), para todas las funciones f ygy todos los números reales a y b. Regla de la potencia (Regla del polinomio): Si Regla del producto: fg f g fg f ( x ) x r , para todo r real, entonces para todas las funciones f y g. f f g fg fg f g fg cociente: g g 2 f ( x ) h( g( x )), si g es diferente de cero. Regla de la cadena: si Funciones inversas y diferenciación: Si y f ( x ) , entonces su inversa dx 0 f 1( x ) . entonces son diferenciables, entonces dy 1 dx dx dy x f 1( y ), y si f ( x ) y para los casos en que y cuando dy 0 . Diferenciación implícita: Si Para las funciones logarítmicas: f ( x , y ) 0 es una función implícita, s e tiene que: f dy x f dx y f ( x ) e x f (x) e x f ( x ) ln ( x ) f (x) La derivada de e elevado a x es e elevado a x 1 La derivada del logaritmo natural (ln) de x es 1 dividido entre x x Para las funciones trigonométricas: f ( x ) sen ( x ) f (x) cos (x) La derivada del seno de x es el coseno de x. f ( x ) cos ( x ) f (x) sen (x) La derivada del coseno x es menos seno de x. f ( x ) tan ( x ) f (x) sec2 (x) La derivada de la tangente de x es la secante al cuadrado de x. f ( x ) cot an ( x ) f (x) Csc2 (x) La derivada de cotangente de x es menos cosecante al cuadrado de x. f ( x ) sec ( x ) f (x) sec (x) tan (x) La derivada de la secante de x es el producto de la secante de x por la tangente de x. f ( x ) csc ( x ) f (x) csc (x) cotan (x) La derivada de la cosecante de x es el producto de menos cosecante de x por la cotangente de x. Extensión del concepto de derivada Cuando una función depende de más de una variable, se utiliza el concepto de derivada parcial. Las derivadas parciales se pueden pensar informalmente como tomar la derivada de una función con respecto a una de ellas, manteniendo las demás variables constantes. Las derivadas parciales se representan como x (en donde ; es una 'd' redondeada conocida como 'símbolo de la derivada parcial'). El concepto de derivada puede ser extendido de forma más general. El hilo común es que la derivada en un punto sirve como una aproximación lineal a la función en dicho punto. Quizá la situación más natural es que las funciones sean diferenciables en las variables. La derivada en un cierto punto entonces se convierte en una transformación lineal entre los correspondientes espacios tangenciales y la derivada de la función se convierte en un mapeo entre los grupos tangenciales. Para diferenciar todas las funciones continuas y mucho más, se puede definir el concepto de distribución. Para las funciones complejas de una variable compleja, la diferenciabilidad es una condición mucho más fuerte que la simple parte real e imaginaria de la función diferenciada con respecto a la parte real e imaginaria del argumento. Por ejemplo, la función f ( x iy ) x 2iy satisface lo segundo, pero no lo primero. También conocido como función holomórfica. Referencias bibliográficas. Calculus of a Single Variable: Early Transcendental Functions (3a edición) por Bruce H Edwards, Robert P. Hostetler, y Ron Larson (2003). Calculus (2a edición) por Michael Spivak. Calculus Early Trascendentals (6a edición) por James Stewart. Principios de Análisis Matemático por Enrique Linés Escardo. http://es.wikipedia.org/wiki/C%C3%A1lculo_diferencial