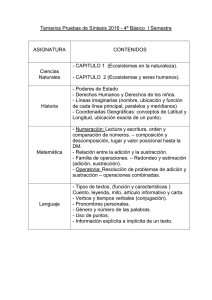
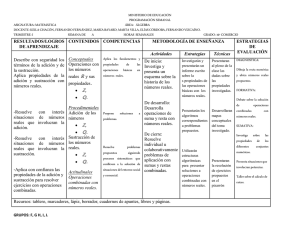
cli - Colegio Bello LaSalle
Anuncio

: Colegio la Salle Bello “De la mano con nuestras familias” CONTENIDO DEL PLAN DE ÁREA 1. IDENTIFICACIÓN DEL ÁREA NOMBRE: Área de Matemáticas ASIGNATURAS: Aritmética Geometría Algebra Trigonometría Calculo Estadística JEFE: Iván Andrés Giraldo Salguero INTEGRANTES: Liliana María Arango Jaramillo Gloria Liliana Castaño Vásquez Ana Milena Cano Restrepo Tatiana Vanesa Betancur Montoya Juan Manuel Álzate Cano Arnaldo José Manchego Pérez. 1.1 POBLACIÓN BENEFICIADA: El colegio La Salle Bello es un centro educativo al que asisten aproximadamente 1300 estudiantes de ambos sexos, distribuidos en los niveles de preescolar, básica y media académica; que se benefician del trabajo que el colegio realiza con el apoyo permanente de los Hermanos de las Escuelas Cristianas y los seglares. De igual manera, los docentes que integran el área se verán beneficiados, pues ésta será una guía que oriente sus labores y cualifique los procesos que se desarrollan en ella. 2. JUSTIFICACIÓN El papel de las Matemáticas es fundamental en todo el proceso de transformación que el hombre ha alcanzado en diferentes aspectos, desde lo social, lo político, lo cultural, hasta las ciencias más abstractas y complejas. Es por lo anterior que se reconoce que “las actividades propias de esta área pueden estimular la actividad y las operaciones mentales, activar la capacidad de razonamiento y de pensamiento crítico y creativo, generar procesos mentales superiores, contribuir a organizar la mente y a formar para la toma de decisiones y para la formulación, análisis y Solución de problemas1. Es por esto que hace parte del proceso educativo de instituciones que tienen como objetivo promover condiciones que favorezcan el desarrollo integral de niños, jóvenes y adultos que pueden contribuir a transformar los contextos. Como resultado de toda esta transformación y con base en el trabajo desarrollado a nivel distrital en el área durante estos últimos siete años, se presenta uno de los elementos unificadores 2 y de gran importancia para el desarrollo del área de los colegios de La Salle en el Área Metropolitana. El área de matemáticas pretende entonces, afianzar dichos procesos desde propuestas metodológicas consecuentes con los contextos y las necesidades de los educandos, con el fin de encaminarlos a una comprensión significativa de conceptos que los lleve a la solución de problemas y al desarrollo de habilidades pertinentes para enfrentar los avatares del diario vivir. Para lograr dar cuenta de ello, es necesario reflexionar sobre el aprendizaje de las matemáticas escolares, el cual está íntimamente vinculado a la didáctica utilizada por el maestro en el aula de clase. 3. DIAGNÓSTICO Con base a los resultados de la autoevaluación del año anterior, El Colegio La Salle Bello se perfila como una institución que implementa en su cotidianidad la participación de pruebas censales a nivel interno y externo. A nivel externo el colegio y el área de matemáticas se han medido con las pruebas Saber, no solo en el grado undécimo sino también en los grados tercero, quinto y noveno. Estas pruebas tienen por objeto “obtener, procesar, interpretar y divulgar información confiable y análisis pertinentes sobre el estado de la educación en el país que satisfagan la demanda social, servir de base para tomar decisiones en las diferentes instancias del servicio educativo y para definir o reorientar políticas que fortalezcan la reforma educativa en marcha. Estas pruebas evalúan los componentes Numérico–Variacional, aleatorio y Geométrico–Métrico, además de las competencias matemáticas de Interpretación y Representación, Formulación y Ejecución, Razonamiento y Argumentación. A continuación se presentan algunos resultados comparativos y análisis respectivos de las pruebas saber 3°,5° y 9° del 2013 del Colegio La Salle Bello: 1 Tomado del Ministerio de Educación Nacional. Documento de Renovación Curricular de Matemáticas, Planteamientos Generales 1987. Santa Fe de Bogotá. 2 Resultados prueba saber, Resultados pruebas externas 2013-2014 3.1 ANÁLISIS DE LOS COMPARATIVOS Grado tercero: Matematicas Grado 3º 50% 44% 40% 39% 39% 38% 37% 30% 26% 20% SATISFACTORIO 10% 0% la Presentación VARIABLES Nuestra San Francisco San Señora de de Asis Buenaventura Chiquinquirá la Presentación Nuestra Señora Nazareth San de Francisco de Chiquinquirá asís Salle Bello San Buenaventura Nazaret Salle Bello SATISFACTORIO 44% 39% 39% 38% 37% 26% AVANZADO 33% 49% 40% 44% 53% 67% DIFERENCIA 23% 12% 21% 18% 10% 7% Observamos que los otros colegios tienen más porcentajes en insuficiente y mínimo dándonos la ventaja en este grado. Variables Salle Bello Satisfactorio 26% Avanzado 67% Diferencia 7% Este 7% se encuentra en insuficiente y mínimo, lo que debemos buscar es que de este porcentaje pase a satisfactorio un buen número de estudiantes y de la escala del 26% del satisfactorio, pasen a nivel avanzado un buen porcentaje de estudiantes permitiendo que aumente este ítem. Matematicas Grado 3º 80% 70% 60% 50% 40% 30% 20% 10% 0% 67% 49% 53% 40% 44% 33% AVANZADO Es claro que los resultados de avanzado se deben aumentar manteniendo un promedio de aumento. 3.2. Grado Quinto: Matematicas Grado 5º 60% 50% 50% 43% 40% 30% 33% 36% 33% 20% 10% 0% SATISFACTORIO 0% Nuestra la VARIABLES Presentación Señora San de Francisco de Chiquinquirá Asís San Buenaventura Nazaret Salle Bello SATISFACTORIO 50% 33% 36% 0% 33% 43% AVANZADO 32% 24% 28% 0% 41% 29% DIFERENCIA 18% 43% 36% 100% 26% 28% Observamos que de los cinco colegios somos el tercer colegio que tiene más porcentajes en insuficiente y mínimo dándonos un dato regular. Salle Bello Diferencia Variables Satisfactorio 43% Avanzado 28% 29% Es importante resaltar que tenemos un 43% en satisfactorio dato que nos permite con mucho trabajo el poder pasar un buen porcentaje ha avanzado, teniendo claro que debemos reforzar los niveles bajos para disminuir ese 28%. Matematicas Grado 9º 80% 70% 60% 50% 40% 30% 20% 10% 0% 71% 39% 10% 17% 11% 12% AVANZADO 3.3. Grado Noveno: Matematicas Grado 9º 60% 50% 40% 30% 20% 10% 0% 52% 55% 50% 40% 32% 21% SATISFACTORIO Nuestra la VARIABLES Presentación Señora San de Francisco de Chiquinquirá Asís San Buenaventura Nazaret Salle Bello SATISFACTORIO 55% 32% 21% 40% 52% 50% AVANZADO 10% 17% 71% 11% 12% 39% DIFERENCIA 35% 51% 8% 49% 36% 11% Observamos que de los seis colegios somos el segundo colegio que tiene menos porcentajes en insuficiente y mínimo dándonos un dato óptimo con ese 11%. Variables Salle Bello Satisfactorio 50% Avanzado 39% Diferencia 11% Aunque es claro que existe una gran diferencia con el colegio San Francisco de Asís, pero es bueno recalcar que tenemos un 50% en satisfactorio dato que nos permite trabajar con un buen panorama para aumentar a avanzado. Matematicas Grado 9º 80% 60% 40% 20% 0% 71% 10% 17% 11% 39% 12% AVANZADO 3.4. Grado Undécimo: Presentamos los resultados del grado undécimo realizando el seguimiento desde el 2006 hasta el presente año 2014, presentando un crecimiento importante en el 2014, al igual que las variaciones durante los diferentes años. Podemos encontrar que en el 2010 y 2014 las desviaciones de dichos datos han sido importantes, fue muy preocupante que en el 2010 no se hubieran tomado medidas estratégicas para mantener los resultados y confirmar el ascenso del promedio, el 2015 será un gran reto para mantener los resultados aplicando las estrategias que se plantearan para dicho año y que se presentaran más adelante en este plan de área. HISTORICO PRUEBA SABER MATEMÁTICAS Año Promedio Variación Año 2006 48,73 48,73 Año 2007 50,91 2,18 Año 2008 48,76 -2,15 Año 2009 52,74 3,98 Año 2010 58,66 5,92 Año 2011 53,50 -5,16 Año 2012 53,78 0,28 Año 2013 54,40 0,62 Año 2014 60,21 5,81 HISTORICO PRUEBA SABER MATEMÁTICAS 70,000 65,000 60,000 60,21 58,66 55,000 50,000 52,74 50,91 53,50 53,78 54,40 Promedio 48,76 48,73 45,000 40,000 Año 2006 Año 2007 Año 2008 Año 2009 Año 2010 Año 2011 Año 2012 Año 2013 Año 2014 Histórico de los últimos 3 años: Con más detenimiento observaremos la proyección del año 2015, propuesta a alcanzar con el fin de afianzar los resultados y proyectar un mejor promedio para el 2016. COMPARATIVO ULTIMOS TRES AÑOS "Proyección" Año Promedio Variación Año 2012 53,78 0,28 Año 2013 54,40 0,62 Año 2014 60,21 5,81 Año 2015 65,00 4,79 COMPARATIVO ULTIMOS TRES AÑOS "Proyección" 66,000 65,00 64,000 62,000 60,000 60,21 58,000 Promedio 56,000 54,000 53,78 54,40 52,000 50,000 Año 2012 Año 2013 Año 2014 Año 2015 Variacíon 7,000 6,000 5,810 5,000 4,000 Variacíon 3,000 2,000 1,000 0,280 0,620 ,000 Año 2012 Año 2013 Año 2014 Con un buen detalle observamos el crecimiento con referencia a los 2 años anteriores, esperamos con gran compromiso proyectar y afianzar los promedios para los próximos tres años siguientes. 3.5.Estrategias implementadas en el 2014: Desde la jefatura de matemáticas planteamos desde el principio de año que lo que debemos trabajar con el estudiante es el CONCEPTO. Concepto ya que si el estudiante tiene claro lo que debe trabajar, lo que debe aprender y lo que debe aplicar, es más fácil que lo incursionemos con éxito en esta estrategia, ya que si el concepto lo tengo claro este me permite interpretar y representar acertadamente, el concepto me permite ejecutar y formular adecuadamente y el concepto me permite razonar y argumentar perfectamente, esta es nuestra primera estrategia que estamos usando desde primaria y bachillerato con el cuerpo docente respectivo. Adicional, esto nos ha permitido seguir las recomendaciones desde la coordinación y rectoría, que consiste en ir familiarizando al estudiante con las competencias y componentes que se van a evaluar durante todo el año. Así mismo aplicándolo en las pruebas internas como la PAL, Pruebas Externas y diferentes exámenes que se realicen dentro del aula, teniendo en cuenta los criterios que evalúa el ICFES sin nombrarles este aspecto formalmente al estudiantado. 4. MARCO REFERENCIAL. Enfoque del área Como área nos interesa estimular el pensamiento matemático en todo el estudiantado, este pensamiento nos permite sistematizar y contextualizar el conocimiento de las matemáticas. Este tipo de pensamiento se desarrolla a partir de conocer el origen y la evolución de los CONCEPTOS y las herramientas que pertenecen al ámbito matemático. Al desarrollar este pensamiento, el sujeto alcanza una formación matemática más completa que le permite contar con un cuerpo de conocimientos importante que le será de utilidad para llegar a los resultados. El área de matematicas apuesta a trabajar fuertemente en el Enfoque Cognitivista y Heuristico. Enfoque cognitivista: Este enfoque monta toda su estructura a partir del concepto y cuando logramos estimular y proyectar este enfoque aseguramos en todo el estudiantado la adquisicion de nuevos aprendizajes en matematicas. Cuando se trabaja el concepto buscamos trabajar la atencion, la memoria e incursionamos en los conocimientos previos como: según neisser (1967), leflore (2000) y piaget (1978) La conexión con el mundo concreto. Los declarativos y los procedimentales. Es claro que al trabajar el enfoque cognitivista cumplimos unos principios como: Establecer relaciones conceptuales. Conexión e integracion para la restructuracion y representaciones matemáticas. El conocimiento declarativo y procedimental deben ser enseñados explicitamente. Conocimientos adquiridos en ditintos contextos Analisis de errores sistematicos. Los procesos motivacioneles y sociales. Enfoque Heurístico: El contexto más adecuado para ejercitar este enfoque es en la resolución de problemas, ya que este permite múltiples formas de ejercitar y reflexionar sobre procesos, como la inducción, la deducción, la generalización y la particularización, que son las claves del pensamiento heurístico y aunque están presentes en otros campos de la actividad humana y de las matemáticas, la resolución de problemas lo dotan de un significado muy preciso. 5. FUNDAMENTOS 5.1. Fundamentos teleológicos. Partiendo de una visión global, es necesario remontarse al principio del saber con el fin de indagar y descubrir la naturaleza del conocimiento y de la realidad, utilizando la razón y los argumentos racionales. Esta actividad de conocer va a permitir actuar como sujeto cognoscente de los objetos, para así poder explicar lo que ocurre en su realidad y a su vez pasar de hombre objeto a hombre sujeto estableciendo un proceso de pensamiento reflexivo y luego científico. Se trata de corresponder el pensamiento con la acción y esto es posible lograrlo, a través de una formación profesional donde el discernimiento intelectual vaya más allá de la simple expectativa, concatenar las ideas del saber, comprenderlas, internalizarlas, adaptarlas y así aprovechar todo ese bagaje de ideas que son el eje central de un modo de educar pertinente. Según Tueros (1998) "Es necesario la elección filosófica en el educador, ya que no existe educación sin alternativa filosófica, entendida ésta en su sentido más amplio de afirmación de valores" (p.2). La acción docente necesita estar vinculada con la finalidad de la educación, en correspondencia con el producto que se quiere obtener, al establecer un modelo que conlleve al perfil del docente deseado, reflejando lo óptimo del ser humano y acorde con las necesidades de la sociedad. A la par poseer una base filosófica, amplia y bien estructurada, que le permita al docente conformar su propia ideología. La adquisición de estos fundamentos filosóficos se fundamentará en una formación académica pertinente; Fourez (1994) difiere de los saberes espontáneos, y en consecuencia plantea que: "...resulta imposible trabajar la filosofía sin adquirir cierta técnica y un adecuado vocabulario... para discernir sobre las cuestiones humanas y la problemática social" (p.12). Es así como se observa una interacción o vínculo entre la filosofía y la educación, unidas permiten perfeccionar y mejorar la enseñanza. 5.2. Fundamentos legales. El Marco Legal, en el que se sustenta el Plan de Área parte de los referentes a nivel normativo y curricular que direccionan el área. En este caso se alude en primera instancia a la Constitución Nacional, estableciendo en el artículo 67, “la educación como un derecho de toda persona y un servicio público que tiene una función social”, siendo uno de sus objetivos, la búsqueda del acceso al conocimiento, a la ciencia, la técnica y a los demás bienes y valores de la Cultura”, por lo que el área de matemáticas no es ajena al cumplimiento de este. Continuando, se presenta la Ley General de Educación (Ley 115 de 1994), la cual en sus artículos 21, 22 y 23 determina los objetivos específicos para cada uno de los ciclos de enseñanza en el área de matemáticas, considerándose como área obligatoria. De otro lado, el desarrollo del proceso educativo, también se reglamenta en el Decreto 1860 de 1994, el cual hace referencia a los aspectos pedagógicos y organizativos, resaltándose, concretamente en el artículo 14, la recomendación de expresar la forma como se ha decidido alcanzar los fines de la educación definidos por la Ley, en los que interviene para su cumplimiento las condiciones sociales y culturales. Dos aspectos que sustentan el accionar del área en las instituciones educativas. Luego, otro referente normativo y sustento del Marco Legal, es la Ley 715 de 2001, donde en su artículo 5, explica “la necesidad por parte de la Nación de establecer las Normas Técnicas Curriculares y Pedagógicas para los niveles de la educación preescolar, básica y media, sin que esto vaya en contra de la autonomía de las instituciones educativas y de las características regionales, y definir, diseñar y establecer instrumentos y mecanismos para el mejoramiento de la calidad de la educación, además, de dar orientaciones para la elaboración del currículo, respetando la autonomía para organizar las áreas obligatorias e introducir asignaturas optativas de cada institución”. En concordancia con las Normas Técnicas Curriculares, es necesario hacer referencia a los “Documentos Rectores”, tales como Lineamientos Curriculares y Estándares Básicos de Competencias, los cuales son documentos de carácter académico no establecidos por una norma jurídica o ley. Ellos hacen parte de los referentes que todo maestro del área debe conocer y asumir, de tal forma que el desarrollo de sus prácticas pedagógicas den cuenta del Plan de Estudios de Matemáticas. En cuanto a los Lineamientos Curriculares en matemáticas publicados por el MEN en 1998, se exponen reflexiones referente a la matemática escolar, dado que muestran en parte los principios filosóficos y didácticos del área estableciendo relaciones entre los conocimientos básicos, los procesos y los contextos, mediados por las Situaciones Problemáticas y la evaluación, componentes que contribuyen a orientar, en gran parte, las prácticas pedagógicas del maestro y posibilitar en el estudiante la exploración, las conjeturas, el razonamiento, la comunicación y el desarrollo del pensamiento matemático. Finalmente, los Estándares Básicos de Competencias (2006), es un documento que aporta orientaciones necesarias para la construcción del currículo del área, permitiendo evaluar los niveles de desarrollo de las competencias que van alcanzando los estudiantes en el transcurrir de su vida estudiantil, además, presenta por niveles la propuesta de los objetos de conocimiento propios de cada pensamiento matemático, los cuales deben estar contextualizados en situaciones Problémicas que son uno de los caminos que permiten un proceso de aprendizaje significativo en el estudiante. 5.3. Fundamentos epistemológicos. Una característica de las tendencias cambiantes en la investigación en educación matemática durante los años recientes ha sido el interés creciente y la focalización sobre el desarrollo de procesos de aprendizaje que le permita al individuo ser considerado un ser social con valores, y estar en capacidad de resolver cuestionamientos que le permita utilizar el pensamiento lógico, prepararse para la ciencia, la tecnología e innovación; los cuales no son tarea exclusiva de las matemáticas sino de todas las áreas de la educación básica y media. Desde la visión socio-cultural “el papel jugado por el contexto social en el desarrollo de los individuos o de los grupos ha sido teorizado implícita o explícitamente, de muchas maneras; lo que demarca los intereses actuales es un desplazamiento desde la identificación de factores sociales como el dominio de lo afectivo a una preocupación con la parte que el entorno social y cultural juega como un todo en el desarrollo del niño. Con relación al conocimiento, estos intereses reflejan un apartase del conocimiento como un a priori y también un apartarse del conocimiento como lo que se construye individualmente hacia el conocimiento como socialmente construido y justificado. (Wittgenstein, 1953, 142) (p. 847). Pero hay una realidad que preocupa a los docentes investigadores, es el trabajo o construcción que se realiza en el aula de clases y según (Balacheff, 1990b): “Debemos reconocer que la mayor parte del tiempo los estudiantes no actúan como hombres teóricos sino como prácticos. Su tarea es dar una solución al problema que el profesor les ha dado, una solución que sea aceptable en relación la situación de la clase. En este contexto la cosa más importante es ser eficiente, no ser riguroso. Se trata de producir una solución, no producir conocimiento... Esto significa que por encima de las características sociales de la situación de enseñanza debemos analizar la naturaleza del objetivo pretendido. Si los estudiantes ven el objetivo como 'hacer', más que como 'conocer', entonces sus... conductas argumentativas podrían verse más como siendo 'económicas' que como conductas matemáticas. (Balacheff, 1990b)” Lo anterior ha llevado a cambios significativos en la enseñanza-aprendizaje de las matemáticas iniciándose así la renovación; según De Guzmán (2007), tuvo como principales características y efectos lo siguiente: Pretendió profundizar en el rigor lógico, en la comprensión, contraponiendo ésta a los aspectos operativos y manipulativos. Esto condujo de forma natural al énfasis en la fundamentación a través de las nociones iniciales de la teoría de conjuntos y en el cultivo del álgebra, donde el rigor es fácilmente alcanzable. La geometría elemental y la intuición espacial sufrió un gran detrimento. Ya que la geometría es, en efecto, mucho más difícil de fundamentar rigurosamente. Con respecto a las actividades fomentadas, la consecuencia natural fue el vaciamiento de problemas interesantes, en los que la geometría elemental tanto abunda, y su sustitución por ejercicios muy cercanos a la mera tautología y reconocimiento de nombres, que es, en buena parte, lo que el álgebra puede ofrecer a este nivel elemental” (p.22). Actualmente la propuesta constructivista (basada en teorías cognitivas de Piaget, Ausbel y Vigotsky) sostiene que para abordar el problema epistemológico es imprescindible utilizar como base empírica, al lado de los hechos que proporciona la historia de la ciencia, los que proporciona el estudio del desarrollo psicogenético (Gascón, 2007: 144). De este enfoque se derivan modelos docentes constructivistas que relacionan -aunque sea parcialmente- el momento exploratorio con el momento de la actividad matemática en el que se elaboran justificaciones e interpretaciones de la práctica matemática. Los modelos constructivistas se pueden clasificar en dos. El primero, llamado por Gascón (2007) constructivismo psicológico, prioriza los procesos psicológicos sobre la relevancia de la actividad matemática, con ello no logra vencer la descontextualización de los problemas al utilizarlos sólo como medio para acceder a un conocimiento. El otro, modelizacionismo, interpreta aprender matemáticas como un proceso de construcción de conocimientos matemáticos relativos a un sistema, que se lleva a cabo mediante la utilización de un modelo matemático de dicho sistema. De esta forma, casi por definición, resulta que en el modelizacionismo la descontextualización de los problemas desaparece hasta el punto de llegar a identificarse el objetivo de la resolución de los problemas, con la obtención de conocimientos sobre el sistema modelizado. La actividad de resolución de problemas se engloba, por tanto, en una actividad más amplia que puede llamarse modelización matemática. Este modelo contempla situaciones problemáticas que abarcan momentos exploratorios y tecnológico-teóricos, dando importancia al papel de la actividad de resolución de problemas sin olvidar el trabajo de la técnica en el aprendizaje de las matemáticas. La unión de ambos momentos remite a un concepto de modelización, que entraña los siguientes estadios: a. la presentación de una situación problemática que formule preguntas y conjeturas con poca precisión en la que se pueden detectar algunas soluciones matemáticas, b. la definición o delimitación del proceso a seguir, es decir, la elaboración del modelo correspondiente, c. el trabajo técnico dentro del modelo, su representación, su interpretación y resultado y d. el planteamiento de nuevos problemas con nuevos modelos a probar. Según Gascón, en el modelizacionismo el objetivo de la actividad matemática -y por tanto el de la enseñanza de las matemáticas- es la obtención de conocimientos relativos a un sistema modelizado que, en principio, puede ser tanto matemático como extra matemático. Los problemas sólo adquieren pleno sentido en el contexto de un sistema; así la resolución de un problema pasa siempre por la construcción explícita de un modelo del sistema subyacente y tiene como objetivo la producción de conocimientos relativos a dicho sistema. Por todas estas razones, el modelizacionismo, que como se dijo se fundamenta en la epistemología constructivista, puede ser considerado como un constructivismo matemático. 5.4. Fundamentos pedagógicos. A través de los siglos han existido movimientos, educativos que han venido criticando sistemáticamente la pedagogía tradicional, la cual se fundamenta en la trasmisión de conocimientos en forma verbal y por medio de textos, siendo la memorización la parte fundamental del aprendizaje dejando a un lado la participación activa y reflexiva del estudiante y del conocimiento del medio real en el que vive.La concepción pedagógica propuesta en el área de matemáticas, geometría y estadística se fundamenta en los principios de la escuela activa, en que el estudiante participa real y reflexivamente de los aprendizajes del saber, para poder actuar con eficiencia del proceso de aprendizaje que debe repercutir en la comunidad en la cual se desempeña. 5.5. Fundamentos sociológicos. Desde una perspectiva sociológica, se caracteriza la enseñanza de las matemáticas como una práctica social en la que se juega la autoridad de esta ciencia como herramienta fundamental para adquirir y consolidar el conocimiento. Las razones para ello son: En primer lugar, las matemáticas obligan a definir claramente las variables de interés encada problema, a establecer las hipótesis sobre su comportamiento y a definir las relaciones entre ellas. En segundo lugar, el lenguaje matemático permite importar a las otras ciencias modelos de relación entre variables que, ofreciendo nuevas posibilidades de explicación de los fenómenos sociales y enriqueciendo el conjunto de modelos disponibles para investigar la realidad social. En tercer lugar, la creciente disponibilidad de datos, debido a la difusión de la tecnología y la automatización en todas las actividades humanas, permite contrastar con mayor rigor los modelos sociales en la práctica mediante los métodos estadísticos y generar predicciones y reglas de comportamiento verificables con los datos. Los modelos matemáticos aportan el lenguaje y la estructura conceptual necesaria para expresar reglas generales de comportamiento y obtener predicciones de validez general. Su utilización facilita que los conocimientos adquiridos puedan transmitirse con precisión, estimulando la comunicación entre distintas áreas. 5.6. Fundamentos psicológicos. De acuerdo con las teorías cognitiva nuestra población estaría demarcada en los siguientes periodos en el desarrollo evolutivo: “Periodo, desde 2 a 6 años”: llamado periodo pre operacional. Se observa que los niños son capaces de utilizar el pensamiento simbólico, que incluye la capacidad de hablar. Los humanos utilizamos signos para conocer el mundo y los niños ya los manejan en este periodo. Sin embargo, este pensamiento simbólico es todavía un pensamiento egocéntrico, el niño entiende el mundo desde su perspectiva. “Periodo, desde los 7 a los 11 años”: periodo de las operaciones concretas. En este periodo el niño puede aplicar la lógica, aplica principios. El niño ya no conoce intuitivamente sino racionalmente. Sin embargo, no maneja todavía abstracciones. Su pensamiento está anclado en la acción concreta que realiza. Es el periodo escolar. “Periodo, de los 12 años en adelante”: periodo de las operaciones formales. Hablamos del adolescente y del adulto. Es la etapa del pensamiento abstracto, no solo piensa de la realidad, sino cómo puede hacer las cosas. El colegio ha trabajado durante los últimos años en potenciar, desde los primeros grados de la básica primaria, los pensamientos espacial, métrico y aleatorio, como consecuencia se trabaja una hora de la semana tanto geometría como estadística, permitiendo establecer una disciplina de trabajo en asignaturas como estadística y geometría además de mostrar mejora en resultados en cuanto a procesos evaluativos externos como en las pruebas saber y el examen de estado del ICFES. 6. MARCO TEÓRICO REFERENTES TEÓRICOS “OBJETO DE CONOCIMIENTO MATEMÁTICO” El objeto del conocimiento de las matemáticas está enfocado a lo sistemático con énfasis del pensamiento numérico, espacial, métrico, aleatorio y Variacional. “El conocimiento matemático está conectado con la vida social de los hombres, que se utiliza para tomar determinadas decisiones que afectan a la colectividad… desde esta perspectiva el conocimiento matemático tiene que ver con las abstracciones, las demostraciones y las aplicaciones pero sin dejar de lado el componente práctico de la actividad matemática dado que su valor principal está en que organiza y da sentido a una serie de prácticas, a cuyo dominio hay que dedicar esfuerzo individual y colectivo” 3. Para el estudio de las matemáticas es fundamental la relación que hay entre el conocimiento y la lógica de comunicación, ya que da a conocer la manera de operar con razonamiento, observación, descripción, comparación, clasificación y relación. El planteamiento en este punto, busca ir un poco más allá de las líneas básicas del enfoque matemático – comunicativo. La razón de ser de esta reorientación es recoger recientes conceptualizaciones e investigaciones en el campo matemático y con conocimientos básicos pensamientos y sistemas 3 IBID. Página 26. numéricos, espacial – geométrico, métrico – medida, aleatorio – datos, variaciones – algebraico y analítico y razonamiento. En este sentido, la concepción de las matemáticas tiene una orientación hacia la construcción de la significación a través de los múltiples códigos y formas que simbolizar, significación que se da en complejos procesos históricos, sociales y culturales en los cuales se constituyen los sujetos en y desde el pensamiento matemático. Las matemáticas más que un sistema de signos y reglas se debe entender como un patrimonio cultural en el sentido de comprender el desarrollo del sujeto en términos del desarrollo de la función simbólica, lógica, matemática, contacto entre la mente del sujeto y el simbolismo lógico. Teniendo en cuenta las habilidades lógicas, es posible concebir desde una orientación hacia la significación de procesos como: leer, escribir, analizar y escuchar matemáticamente. Los ejes temáticos nos sirven como referente del trabajo curricular, ellos son: eje numérico, eje métrico, eje geométrico, eje estadístico y eje analítico. En lo concerniente al área de matemática, ocho competencias fundamentales deben ser desarrolladas teniendo como base los ejes curriculares, estas son: Pensar y razonar. Argumentar. Comunicar. Modelar. Plantear y resolver problemas. Representar. Utilizar lenguaje y operaciones simbólicas, formales y técnicas. Utilizar ayudas y herramientas. El documento expedido por el Ministerio Nacional, recoge lo mejor de la renovación curricular. “con los lineamientos se pretende atender a la necesidad de orientaciones y criterios nacionales sobre currículos, sobre la función del área y sobre los nuevos enfoques para comprenderla y enseñarla… los lineamientos buscan fomentar el estudio de la fundamentación pedagógica de las disciplinas, el intercambio de experiencias en el contexto de los PEI”4 Los lineamientos curriculares de matemáticas en primer lugar, propone unos referentes curriculares muy amplios, que combinan certeramente los procesos generales, los contextos y los conocimientos básicos. En segundo lugar representa un gran proceso al ubicar los sistemas matemáticos como herramientas básicas para el pensamiento matemático de cada tipo, privilegiando los procesos de pensamiento, 4 IBID página 11. para los cuales los sistemas son las herramientas privilegiadas de cada tipo de pensamiento, que nunca se agotan. En tercer lugar, la propuesta de trabajar por medio de situaciones problemáticas, más ricas que los meros ejercicios de mecanización o problemas de rutina. 6.1. LAS SITUACIONES PROBLEMAS El estudiante es competente, cuando sabe aplicar el conocimiento; no basta saber, hay que saber hacer. Cuando los educandos, abordan una situación problemática como contexto, y lo resuelven, logran desarrollar el pensamiento matemático, que los habilita para producir conocimiento. A medida que utilice esta metodología, en las diversas áreas de su interés, le queda claro tanto la utilidad como el sentido de ella; será posible entonces, crear nuevos conceptos, desarrollar habilidades en la solución de problemas futuros en cualquier disciplina del saber. Hoy tradicionalmente el maestro trabaja fuera del contexto donde ocurre el aprendizaje porque se deja los problemas y aplicaciones para final del aprendizaje, olvidando que éstos contribuyen a redescubrir nuevos modelos, inventar otros, plantear preguntas. Al partir de situaciones problemáticas, se tiene presente: El alumno manipula, lee, pregunta o discute sobre el contexto dado. Reflexiona sobre su proceso de aprendizaje. Adquiere confianza en si mismo. Se divierte, construye, inventa, crea. Se prepara para resolver problemas de otras disciplinas del saber y enfrenta con capacidad nuevos retos tecnológicos del momento actual, de los cambios culturales y de la ciencia misma. Desde el aprendizaje, utilizando problemas como contexto, será posible que el educando le encuentre sentido y aplicación de la matemática en áreas de su interés o presencia abordándolas con estrategias de análisis, interpretación y justificación, con autonomía y reflexión crítica frente a los retos de la tecnología y de la ciencia hoy. 6.2. PENSAMIENTOS MATEMÁTICOS Pensamiento numérico y sistema numérico: Es la comprensión general que se tiene sobre los números, operaciones, habilidad e inclinación para usar esta comprensión en forma flexible, para hacer juicios matemáticos y desarrollar estrategias útiles para el manejo de números y operaciones.Se adquiere gradualmente y va evolucionando a medida que el alumno tiene la oportunidad de pensar esos números y de usarlos en contextos significativos. Este pensamiento se manifiesta de diversas maneras, de acuerdo al desarrollo matemático que tenga el alumno. Particularmente se manifiesta en el cálculo mental o utilizando medios como la calculadora y especialmente Aplicando el significado de los números en la solución de problemas y las relaciones y operaciones; comprensión de la relación entre el contexto del problema y la relación del mismo. El Ministerio de Educación a través de los lineamientos curriculares propone tres aspectos que pueden ayudar a desarrollar el pensamiento numérico de los niños, a través del sistema de los números naturales: Comprensión de los números y de la numeración a través de experiencias de la vida cotidiana, construcción del sistema de numeración, teniendo en cuenta como base actividades de contar agrupar y el uso del valor posicional. Comprensión del concepto de las operaciones: suma, resta, multiplicación y división de números naturales, reconociendo el significado de la operación en situaciones concretas, de las cuales emergen; identificando los modelos más usuales y prácticos de las operaciones, comprendiendo las propiedades matemáticas de las operaciones, el efecto de cada operación y las relaciones entre ellas. Cálculos con números y aplicaciones de números y operaciones. La finalidad del cálculo es la solución de problemas y no, adquirir destrezas a través de algoritmos formales, muchas veces sin comprender ni los conceptos ni el significado de las operaciones. Pensamiento espacial: El pensamiento espacial hace referencia a un sentido intuitivo de ubicación y no solamente a lo referente a la geometría intuitiva como tal el pensamiento espacial es usado para representar y manipular información para la solución de problemas de ubicación, orientación, distribución de espacios. Este pensamiento se sustenta en la inteligencia espacial, según el autor Howard Gardner en su teoría de las inteligencias múltiples donde la resolución de problemas espaciales requiere de características cognitivas que consideren el entorno físico, cultural e histórico. Las soluciones se apoyan con modelos y figuras; con palabras del lenguaje ordinario, con gestos, movimientos corporales. La geometría activa parte del principio de que todos los conceptos son adquiridos a través del manejo del cuerpo y del espacio real, de las relaciones de los objetos. Pensamiento métrico y sistemas de medidas: Pensamiento métrico puede definirse a la capacidad que tiene una persona para construir, comprender, apreciar, seleccionar y diferenciar conceptos, unidades, magnitudes, haciendo uso apropiado de instrumentos en situaciones específicas. El pensamiento métrico es, entonces, la facultad de aplicar procesos de medición desarrollados desde unas primeras acciones en las que se dio pasos graduales desde la apreciación, diferenciación y caracterización de lo concreto, al pensamiento métrico se llega por la interacción dinámica que genera el proceso de medir entre el entorno, como instancia a conocer, transformar, aprovechar y conservar los estudiantes. Pensamiento aleatorio y sistema de datos: La teoría de la probabilidad es una de las aplicaciones al pensamiento aleatorio favoreciendo el tratamiento de la certidumbre en algunas ciencias como la biología, la medicina, la economía... Y con mayor razón han permitido el desarrollo de la misma matemática. En síntesis, el desarrollo del pensamiento aleatorio significa la resolución de problemas. Según SHANGHNESSY en 1985. “El pensamiento aleatorio en las matemáticas escolares se debe dar mediante los contenidos de la probabilidad y la estadística y que estos siempre conduzcan a la exploración e investigación tanto del docente como del alumno” En las enseñanzas de las matemáticas convencionales enfatizamos en la búsqueda de la respuesta correcta y única, cuando el correcto sería en llevar al alumno a la introducción de la estadística y la probabilidad del currículo de las matemáticas para crear con ellos un mayor uso del pensamiento. Pensamiento variacional, sistemas algebraicos y analíticos: El sistema o pensamiento variacional, los sistemas algebraicos y analíticos, desde el punto de vista matemático posibilitan al estudiante desde un contexto dado vivenciar sus diferentes escenarios: práctico, educativo y científico para romper esquemas y viejos paradigmas que conduzcan a la construcción de nuevas estructuras. Creando así modelos con patrones que van a ser puntos de referencia en cantidades y magnitudes. Es de anotar que el conocimiento no es una copia de la realidad, conocer un objeto no es solamente observarlo, es actuar sobre él, es transformarlo, modificarlos y comprender este proceso. Todo lo anterior, debe conducir a establecer variabilidad en los diferentes escenarios con el fin de que el estudiante aplique el desarrollo de un pensamiento variacional en la solución de situaciones problemáticas, construcción de expresiones numéricas, algebraicas, geométricas, métricas y aleatorias. Implicando así que la construcción de este pensamiento variacional en el estudiante se adquiere algorítmicamente. En conclusión, el estudiante dentro del desarrollo de su pensamiento variacional debe ser capaz de transformar el contexto como muestra de la aprehensión de un nuevo saber o conocimiento. 7. Competencias propias del área. Las competencias matemáticas no se alcanzan por generación espontánea, sino que requieren de ambientes de aprendizaje enriquecidos por situaciones problemas significativos y comprensivos, que posibiliten avanzar a niveles de competencia más complejos. La noción general de competencia ha venido siendo objeto de interés en muchas investigaciones y reflexiones, una síntesis de los resultados de éstas permite precisar que el sentido de la expresión “ser matemáticamente competente” está íntimamente relacionado con los fines de la educación matemática de todos los niveles educativos. Los cinco procesos generales que se contemplaron en los Lineamientos Curriculares de Matemáticas son: formular y resolver problemas; modelar procesos y fenómenos de la realidad; comunicar; razonar, formular comparar y ejercitar procedimientos algorítmicos. 7.1. La formulación, tratamiento y resolución de problemas Este es un proceso presente a lo largo de todas las actividades curriculares de matemáticas y no una actividad aislada y esporádica; más aún, podría convertirse en el principal eje organizador del currículo de matemáticas, porque las situaciones problema proporcionan el contexto inmediato en donde el quehacer matemático cobra sentido, en la medida en que las situaciones que se aborden estén ligadas a experiencias cotidianas y, por ende, sean más signifi cativas para los estudiantes. Estos problemas pueden surgir del mundo cotidiano cercano o lejano, pero también de otras ciencias y de las mismas matemáticas, convirtiéndose en ricas redes de interconexión e interdisciplinariedad. 7.2. La modelación Un modelo puede entenderse como un sistema figurativo mental, gráfico o tridimensional que reproduce o representa la realidad en forma esquemática para hacerla más comprensible. Es una construcción o artefacto material o mental, un sistema –a veces se dice también “una estructura”– que puede usarse como referencia para lo que se trata de comprender; una imagen analógica que permite volver cercana y concreta una idea o un concepto para su apropiación y manejo. Un modelo se produce para poder operar transformaciones o procedimientos experimentales sobre un conjunto de situaciones o un cierto número de objetos reales o imaginados, sin necesidad de manipularlos o dañarlos, para apoyar la formulación de conjeturas y razonamientos y dar pistas para avanzar hacia las demostraciones. En ese sentido, todo modelo es una representación, pero no toda representación es necesariamente un modelo. Análogamente, todo modelo es un sistema, pero no todo sistema es un modelo, aunque cualquier sistema podría utilizarse como modelo, pues esa es la manera de producir nuevas metáforas, analogías, símiles o alegorías. 7.3. La comunicación A pesar de que suele repetirse lo contrario, las matemáticas no son un lenguaje, pero ellas pueden construirse, refinarse y comunicarse a través de diferentes lenguajes con los que se expresan y representan, se leen y se escriben, se hablan y se escuchan. La adquisición y dominio de los lenguajes propios de las matemáticas ha de ser un proceso deliberado y cuidadoso que posibilite y fomente la discusión frecuente y explícita sobre situaciones, sentidos, conceptos y simbolizaciones, para tomar conciencia de las conexiones entre ellos y para propiciar el trabajo colectivo, en el que los estudiantes compartan el significado de las palabras, frases, gráficos y símbolos, aprecien la necesidad de tener acuerdos colectivos y aun universales y valoren la efi ciencia, eficacia y economía de los lenguajes matemáticos. 7.4. El razonamiento El desarrollo del razonamiento lógico empieza en los primeros grados apoyado en los contextos y materiales físicos que permiten percibir regularidades y relaciones; hacer predicciones y conjeturas; justificar o refutar esas conjeturas; dar explicaciones coherentes; proponer interpretaciones y respuestas posibles y adoptarlas o rechazarlas con argumentos y razones. Los modelos y materiales físicos y manipulativos ayudan a comprender que las matemáticas no son simplemente una memorización de reglas y algoritmos, sino que tienen sentido, son lógicas, potencian la capacidad de pensar y son divertidas. En los grados superiores, el razonamiento se va independizando de estos modelos y materiales, y puede trabajar directamente con proposiciones y teorías, cadenas argumentativas e intentos de validar o invalidar conclusiones, pero suele apoyarse también intermitentemente en comprobaciones e interpretaciones en esos modelos, materiales, dibujos y otros artefactos. 7.5. La formulación, comparación y ejercitación de procedimientos Este proceso implica comprometer a los estudiantes en la construcción y ejecución segura y rápida de procedimientos mecánicos o de rutina, también llamados “algoritmos”, procurando que la práctica necesaria para aumentar la velocidad y precisión de su ejecución no oscurezca la comprensión de su carácter de herramientas eficaces y útiles en unas situaciones y no en otras y que, por lo tanto, pueden modificarse, ampliarse y adecuarse a situaciones nuevas, o aun hacerse obsoletas y ser sustituidas por otras. Para analizar la contribución de la ejecución de procedimientos rutinarios en el desarrollo significativo y comprensivo del conocimiento matemático es conveniente considerar los mecanismos cognitivos involucrados en dichos algoritmos. Uno de estos mecanismos es la alternación de momentos en los que prima el conocimiento conceptual y otros en los que prima el procedimental, lo cual requiere atención, control, planeación, ejecución, verificación e interpretación intermitente de resultados parciales. 8. OBJETIVOS 8.1. GENERAL Generar un ambiente favorable hacia las matemáticas y su estudio que permita lograr una sólida comprensión de los conceptos, procesos y estrategias básicas para la resolución de problemas que se presentan en su contexto, satisfaciendo sus necesidades como ciudadano constructivo, comprometido y reflexivo, en aras del planteamiento y solución de problemas de índole científico y tecnológico. 8.2. OBJETIVOS ESPECIFICOS DEL AREA. Ejecutar clases dinámicas y participativas en donde los estudiantes pongan en práctica los conceptos adquiridos. Evaluar actividades para el razonamiento lógico, mediante el dominio de los sistemas numérico, variacional, geométrico, métrico, aleatorio, así como su utilización en la interpretación y solución de problemas de la ciencia o de la vida cotidiana. Construir sus propios argumentos acerca de hechos matemáticos y compartidos con sus compañeros en un ambiente de respeto y tolerancia. Reconocer regularidades y usarlas en la modelación de hechos matemáticos. Los aportes que el área de matemática presenta para el logro de cada uno de los objetivos comunes a todos los educando, son: SER PERSONA Lo que implica que las actitudes asumidas por el alumno frente a las matemáticas demuestran su autonomía, honestidad, espíritu de superación, su interés por el conocimiento y su responsabilidad en la vida cotidiana. INTEGRASE, TRABAJAR Y DECIDIR EN GRUPO Desarrolla habilidades y destrezas en el alumno que demuestren su capacidad de participar e integrase a los diferentes grupos de trabajo; fortaleciendo la participación, la democracia y la sana convivencia. COMUNICARSE Despertando el interés por la lectura y el conocimiento científico. Desarrollando en él capacidad para leer el lenguaje propio del área. DESARROLLAR EL PENSAMIENTO LÓGICO Utilizando diferentes estrategias para resolver problemas, tomar decisiones, permitiendo ser lógicos, independientes y coherentes. ACCEDER Y USAR LA TECNOLOGÍA Utilizando bibliografía, apuntes, prensa, radio, televisión, se forja el espíritu investigativo en el alumno. CAPACIDAD PARA DESCRIBIR, ANALIZAR Y TRANSFORMAR EL ENTORNO NATURAL Y SOCIAL Reconocer la importancia de las matemáticas en la transformación del entorno natural y social. Permitiéndole la construcción de una formación multicultural que le proporcione el respeto por las diferencias de otras culturas o etnias de nuestro país o del mundo. Así mismo, el área de matemáticas hace su aporte, en la identificación colectiva y consensuada de necesidades propias del medio o región donde se vive, de tal manera que conjuntamente, se busquen y apliquen las estrategias pertinentes en la solución de los problemas propios de la comunidad educativa, se establezcan las distintas variables a resolver y se busquen las soluciones de interés general que redunden en el mejoramiento de la calidad de vida como el manejo racional de los recursos o presupuestos familiares o de los costos educativos. Lo anterior entonces, permitirá desarrollar habilidades en la solución de problemas futuros del orden matemático propios de su entorno y de otras regiones. 9. OBJETIVOS POR CICLO. 9.1. Preescolar El crecimiento armónico y equilibrado del niño, de tal manera que facilite la motricidad, el aprestamiento y la motivación para la lecto-escritura y para las soluciones de problemas. El desarrollo de la creatividad, las habilidades y destrezas propias de la edad, como también de su capacidad de aprendizaje. La ubicación espacio-temporal y el ejercicio de la memoria. El estímulo a la curiosidad para observar y explorar el medio natural, familiar y social. La utilización de manera creativa de experiencias, nociones y competencias para encontrar caminos de resolución de problemas y situaciones de la vida cotidiana y satisfacer sus necesidades. La relación de conceptos nuevos con otros ya conocidos. 9.2. Básica primaria: El fomento del deseo de saber, de la iniciativa personal frente al conocimiento y frente a la realidad social, así como del espíritu crítico. El desarrollo de los conocimientos matemáticos necesarios para manejar y utilizar operaciones simples de cálculo y procedimientos lógicos elementales en diferentes situaciones, así como la capacidad para solucionar problemas que impliquen estos conocimientos. La asimilación de conceptos científicos en las áreas de conocimiento que sean objetos de estudio, de acuerdo con el desarrollo intelectual y la edad. El desarrollo de valores civiles, éticos y morales, de organización social y de convivencia humana. La adquisición de habilidades para desempeñarse con autonomía en la sociedad. La expresión de ideas y situaciones que involucran conceptos matemáticos mediante el lenguaje natural y representaciones físicas, pictóricas, gráficas, simbólicas y establecer conexiones entre ellas. La explicación de ideas y justificación de respuestas mediante el empleo de modelos, la interpretación de hechos conocidos y la aplicación de propiedades y relaciones matemáticas. 9.3. Secundaria: El desarrollo de las capacidades para el razonamiento lógico, mediante el dominio de los sistemas numéricos, geométricos, métricos, lógicos, analíticos, de conjuntos, de operaciones y relaciones, así como para su utilización en la interpretación y solución de los problemas de la ciencia, de la tecnología y los de la vida cotidiana. El avance en el conocimiento científico, de los fenómenos físicos, químicos y biológicos, mediante la comprensión de las leyes, el planteamiento de problemas y la observación experimental. La comprensión de la dimensión práctica de los conocimientos teóricos, así como la dimensión teórica del conocimiento práctico y la capacidad para utilizarla en la solución de problemas. La utilización con sentido crítico de los distintos contenidos y formas de información y la búsqueda de nuevos conocimientos con su propio esfuerzo. 9.4. QUE CONOCIMIENTOS NECESITAN LOS ESTUDIANTES DE GRADO PRIMERO EN EL GRADO QUINTO En el grado primero se manejan todos los contenidos que plantea la malla curricular, además en geometría se trabajan diferentes clases de líneas, en estadística se trabajan pictogramas simples (cada imagen representa una unidad o elemento). Se inicia una introducción al pensamiento algebraico, estableciendo la adición y la sustracción como operaciones contrarias (diversos tipos de problemas para la adición según los lineamientos). Los estudiantes del grado primero deberán terminar con la capacidad del significado de los números a partir de sus experiencias en la vida cotidiana, teniendo presente actividades como: contar, agrupar y el uso del valor posicional. Para construir lo anterior se debe implementar con los estudiantes, los diferentes tipos de preguntas para resolver problemas de suma y resta. Variar el tipo de pregunta le permitirá tener una mayor capacidad de razonamiento y desempeño. La comprobación de las operaciones de acuerdo a lo razonable de la respuesta obtenida En el pensamiento métrico se debe enfatizar en el reconocimiento de los instrumentos de medición para algunas medidas. Los estudiantes que terminan el grado segundo empleen y reconozcan las diferentes clases de líneas y su posición en el espacio, además que usen el lenguaje y los términos propios del área y las operaciones matemáticas. Que sepan las tablas de multiplicar y dividan por, al menos una cifra. Que se trabaje el valor posicional, que se maneja como espacio vacío en el algoritmo de la multiplicación. Que el niño identifique el tipo de operación como estrategia para solucionar un problema, sin que el docente indique las operaciones (contextualización de los problemas). Pictogramas, representando mayor cantidad por cada figura (2 y 3) Operaciones mentales, de retención de las cantidades con diferentes operaciones. Trabajo con sólidos y que diferencien con los polígonos. Identifiquen figuras planas y en tres dimensiones, incluso si están representadas en el papel. A partir de una parte oculta en otra que está en frente Que reconozcan y usen de manera correcta los instrumentos de medición como el reloj, el metro o la regla, y determinen el objeto de mayor peso según la representación gráfica de una balanza. Que reconozcan la posibilidad de ocurrencia de eventos (probable, poco probable, seguro, imposible) y que justifiquen según la información dada. Variabilidad a través de secuencias simples de aumento o disminución numérica o en proporción. Para el grado tercero: Mayor énfasis en la solución de situaciones problemas, con diferentes tipologías de preguntas según lineamientos y haciendo uso del lenguaje matemático. Trabajo con cuerpos geométricos la diferencia entre figuras bidimensionales y tridimensionales y sus posibles propiedades físicas. Rodar escribir sobre el objeto. La división por dos cifras con el método de resta implícita o explícita para un mayor rendimiento. Las fracciones deberán ser un punto fuerte para este grado pero las operaciones serán solo con fracciones homogéneas. Los estudiantes de cuarto: Emplea el lenguaje como clave para identificar la operación que debe realizarse en un problema. Diferenciar el uso de la palabra más en problemas de adicción y sustracción. Que reconozcan la suma y la multiplicación como operaciones que aumentas las cantidades y que la resta y la división disminuyen las cantidades. Y así puedan identificar la operación que se usó en un procedimiento. 9.5. QUE CONOCIMIENTOS NECESITAN LOS ESTUDIANTES DE GRADO SEXTO EN EL GRADO NOVENO Pensamiento numérico y sistemas de numeración: Sistemas de ecuaciones lineales. Operaciones básicas con números racionales. Interpretación de información o situaciones problema relacionadas con números naturales y racionales. Pensamiento Variacional: Interpretación de enunciados de cualquier tipo (verbal y escrito). Transformar enunciados verbales a expresiones algebraicas Pensamiento métrico: Transformar diferentes unidades a través de la regla de tres simple. Pensamiento geométrico: Tener conocimiento de áreas y perímetros de figuras geométricas. Trabajo en el plano cartesiano. Pensamiento aleatorio: Ser capaz de interpretar resultados, agruparlos y sacar conclusiones. Hallar medidas de tendencia central y de posición. Reconocer que es un espacio muestral y la probabilidad de un evento. 9.6. QUE CONOCIMIENTOS NECESITAN LOS ESTUDIANTES DE GRADO DECIMO EN EL GRADO UNDECIMO Pensamiento numérico y sistemas de numeración: Que reconozca y clasifique cada conjunto numérico. Sea capaz de realizar todo tipo de operaciones entre los conjuntos numéricos. Sea capaz de interpretar situaciones en las que se requieran operaciones entre conjuntos numéricos. Pensamiento variacional: Transforme enunciados verbales a algebraicos ya sean de tipo oral o escrito. Que reconozca o diferencie una variable de una constante y porque partes está conformado un término. Reconozca cada tipo de ecuaciones y desigualdades (grado y manera de solución). Pensamiento métrico: Transformar diferentes unidades de medida (longitudes, volúmenes, pesos) Pensamiento geométrico: Tener conocimiento de áreas y perímetros de figuras geométricas. Pensamiento aleatorio: Ser capaz de interpretar resultados, agruparlos y sacar conclusiones. Hallar medidas de tendencia central y de posición. Reconocer que es un espacio muestral y la probabilidad de un evento (simple o condicional) Reconozca de manera clara las técnicas de conteo ( principio aditivo, principio multiplicativo, combinación y permutación 10. INCLUSIÓN Las características personales de aquellos estudiantes con distintos ritmos de aprendizaje, capacidades y dificultades, se tendrán en cuenta para adaptaciones curriculares, metodológicas y evaluativas, según las problemáticas relevantes o diagnosticadas por profesionales (criterio de inclusión). Cada docente debe presentar al inicio del período un formato de adaptación curricular que para todos Aquellos estudiantes que así lo requieran; dicho formato debe incluir: Indicador de logro. Actividades Criterios de evaluación. 10.1. LA INCLUSIÓN EN EL ÁREA DE MATEMÁTICAS La Inclusión es un enfoque que responde positivamente a la diversidad de las personas y a las diferencias individuales, entendiendo que la diversidad no es un problema, sino una oportunidad para el enriquecimiento de la sociedad, a través de la activa participación en la vida familiar, en la educación, en el trabajo y en general en todos los procesos sociales, culturales y en las comunidades (Unesco, 2005). Una escuela inclusiva es una comunidad educativa en donde las prácticas pedagógicas responden a la diversidad de sus estudiantes, teniendo en cuenta las necesidades emocionales, académicas y sociales de la institución. La educación inclusiva sólo se lleva a cabo si se introducen al aula estrategias y prácticas diferentes de las utilizadas tradicionalmente (Sánchez, 2005). Este hecho depende ampliamente de la actitud, el conocimiento, la competencia y las competencias del profesorado a la hora de innovar y de crear contextos de aprendizaje que satisfagan las necesidades y el potencial de los estudiantes. Como primer paso es necesario respetar los principios de la educación inclusiva: La no discriminación. La accesibilidad. Las adaptaciones razonables a las necesidades específicas a través de planteamientos flexibles y alternativos para el aprendizaje y la enseñanza. La igualdad de normas. La participación. El apoyo para satisfacer las necesidades relacionadas con la discapacidad y La importancia de la preparación para el mercado laboral. Teniendo en cuenta el informe de la Agencia Europea para el Desarrollo en la Educación Especial (2003) producido sobre la base de numerosas investigaciones, se pueden identificar los siguientes grupos de factores como determinantes de prácticas inclusivas: a. Enseñanza cooperativa b. Aprendizaje cooperativo c. Resolución de problemas colaborativa d. Agrupaciones heterogéneas e. Enseñanza eficaz Las siguientes son algunas prácticas inclusivas o criterios proporcionados por la "Plataforma Ciudadana para una Escuela Inclusiva", (2006) que como área podemos poner en práctica: a. Incluir a todo el alumnado en las diferentes actividades b. Fomentar una cultura de escuela inclusiva. c. Llevar a cabo un trabajo cooperativo eficaz entre los maestros del área. d. Utilizar diversos recursos y estrategias educativas diferenciadas. e. Realizar una programación específica y sistemática f. Evaluar de forma sistemática el progreso del estudiante (cognitiva, emocional, social, relacional, etc.) Y plantear medidas para superar las dificultades. g. Fomentar las actividades extracurriculares. h. Valoran la colaboración con la comunidad. 11. EVALUACIÓN: Concepto ver SIEE. Estándares e indicadores de desempeño para cada componente del área (asignaturas) Criterios de evaluación (SIEE) Procedimientos de evaluación (SIEE) Diseño de planes especiales de apoyo para estudiantes con dificultades en su proceso de aprendizaje. La Evaluación se concibe como una oportunidad para aprender y mejorar, en un proceso permanente, flexible y objetivo que apunta a la formación integral, proporcionando información básica para implementar estrategias pedagógicas que apoyen a los estudiantes con debilidades y desempeños superiores en su proceso formativo. Constituye una propuesta incluyente que contribuye a la calidad, equidad y pertinencia de la educación. Es además una estrategia de aprendizaje que permite valorar o estimar lo logrado por el estudiante en alineación con lo planeado, y le proporciona al docente información para reorientar sus prácticas pedagógicas. La evaluación se caracteriza por ser: Integral: Tiene en cuenta las dimensiones del desarrollo del estudiante, conocimientos, actitudes, comportamientos, valores, desempeños cotidianos que evidencien sus logros a nivel personal y social. Enfatiza en el diálogo como instrumento de reflexión, análisis e indispensable en la solución de los conflictos. Sistemática: Responde a la misión, visión y principios lasallistas, guarda relación con los fines y objetivos de la educación, los Estándares de Competencias, los contenidos del Plan de Estudios y responde a los retos mundiales. Continua: Se realiza en forma permanente, permite observar avances y dificultades en el proceso formativo de los estudiantes. Flexible: Tiene en cuenta las etapas de desarrollo del estudiante, intereses, capacidades, ritmos de aprendizaje, limitaciones de tipo afectivo, familiar, nutricional, entorno social, y da un manejo diferenciado a las problemáticas diagnosticadas. Cualitativa: Aunque se exprese también de manera cuantitativa responde a procesos descriptivos que implican sistemas de planeación, diseño, ejecución y control en la gestión de la calidad. Democrática: Es participativa, colegiada, favorece el trabajo en equipo e implica responsabilidad social. Tiene en cuenta diversas dinámicas como la autoevaluación en los estudiantes, entendida como la valoración y descripción de desempeños sobre sí mismo, apunta a fortalecer la autocrítica y la capacidad para reconocerse en sus debilidades y fortalezas. La coevaluación: Permite que los estudiantes se evalúen entre ellos mismos, mirando y valorando sus desempeños. La hetero- evaluación: Constituye una mirada formativa, valorativa y sumativa sobre los desempeños, elaborada por los maestros hacia sus educandos, y de estos hacia sus docentes 12. LA EVALUACION POR COMPETENCIAS “Para evaluar el nivel de competencia matemática de los alumnos, OCDE / PISA se basa en las ocho competencias matemáticas específicas identificadas por Niss (1999) y sus colegas daneses, estas son: Pensar y razonar: Incluye plantear preguntas características de las matemáticas (“¿Cuántas … hay?”, “¿Cómo encontrar …?”); reconocer el tipo de respuestas que las matemáticas ofrecen para estas preguntas; distinguir entre diferentes tipos de proposiciones (definiciones, teoremas, conjeturas, hipótesis, ejemplos, condicionales); y entender y manipular el rango y los límites de ciertos conceptos matemáticos. Argumentar: Se refiere a saber qué es una prueba matemática y cómo se diferencia de otros tipos de razonamiento matemático; poder seguir y evaluar cadenas de argumentos matemáticos de diferentes tipos; desarrollar procedimientos intuitivos; y construir y expresar argumentos matemáticos. Comunicar: Involucra la capacidad de expresarse, tanto en forma oral como escrita, sobre asuntos con contenido matemático y de entender las aseveraciones, orales y escritas, de los demás sobre los mismos temas. Modelar: Incluye estructurar la situación que se va a moldear; traducir la “realidad” a una estructura matemática; trabajar con un modelo matemático; validar el modelo; reflexionar, analizar y plantear críticas a un modelo y sus resultados; comunicarse eficazmente sobre el modelo y sus resultados (incluyendo las limitaciones que pueden tener estos últimos); y monitorear y controlar el proceso de modelado. Plantear y resolver problemas: Comprende plantear, formular, y definir diferentes tipos de problemas matemáticos y resolver diversos tipos de problemas utilizando una variedad de métodos. Representar: Incluye codificar y decodificar, traducir, interpretar y distinguir entre diferentes tipos de representaciones de objetos y situaciones matemáticas, y las interrelaciones entre diversas representaciones; escoger entre diferentes formas de representación, de acuerdo con la situación y el propósito particulares. Utilizar lenguaje y operaciones simbólicas, formales y técnicas: Comprende decodificar e interpretar lenguaje formal y simbólico, y entender su relación con el lenguaje natural; traducir del lenguaje natural al lenguaje simbólico / formal, manipular proposiciones y expresiones que contengan símbolos y fórmulas; utilizar variables, resolver ecuaciones y realizar cálculos. Utilizar ayudas y herramientas: Esto involucra conocer, y ser capaz de utilizar diversas ayudas y herramientas (incluyendo las tecnologías de la información y las comunicaciones TICs) que facilitan la actividad matemática, y comprender las limitaciones de estas ayudas y herramientas 5”. 5 www.eduteka.org/Pisa2003.php 13. PROCESOS DEL AULA La evaluación es un acto colectivo y debe tener en cuenta los acuerdos y criterios que se elaboren en el proyecto curricular de la institución. Cuando hablamos de evaluación debemos entender que es un proceso permanente, objetivo e integral mediante el cual es valorado, a través de diversas estrategias pedagógicas, el nivel de desempeño de los estudiantes en relación con las competencias. En el decreto aparecen los propósitos principales. Los objetivos de cada nivel se deben dar en relación capacidades de cada estudiante, las cuales están relacionadas con la etapa evolutiva. Para llevar a cabo la evaluación es necesario fomentar en los estudiantes: Comprensión y expresión. Capacidad de identificación y resolución de problemas en los distintos campos del conocimiento. Actitud positiva ante los conocimientos y ante el colectivo educativo. Hábitos de trabajo individual y en grupo. Aplicación de valores lasallistas. 14. ESTRATEGIA METODOLOGICA Las estrategias metodológicas permiten identificar principios, criterios y procedimientos que configuran la forma de actual del docente en relación con la programación, implementación y evaluación del proceso de enseñanza aprendizaje. Estas estrategias constituyen la secuencia de actividades planificadas y organizada sistemáticamente permitiendo la construcción de de conocimiento escolar y en particular intervienen en la interacción con las comunidades. Se refiere a las intervenciones pedagógicas realizadas con la intención de potenciar y mejorar los procesos espontánea de aprendizaje y de enseñanza, como un medio para contribuir a un mejor desarrollo de la inteligencia, la afectividad, la conciencia y las competencias para actuar socialmente. La siguiente tabla expone de manera general como la solución de problemas se convierte una estrategia metodológica que permite evaluar las capacidades de los estudiantes. Tiene en cuenta dos elementos esenciales: la comprensión y expresión que está ligada a la explicación del docente y la comprensión del estudiante y la solución de problemas que se refiere al saber hacer. TABLA Nº 4. COMPRENSIÓN Y EXPRESIÓN IDENTIFICACIÓN SITUACION PROBLEMAS CONCEPTUALIZACIÓN CONTEXTUALIZADA PARTE OPERACIÓN RAZONAMIENTO PROCEDIMIENTOS Utilizar algoritmos para efectuar cada una de las Presentar la definición de las operaciones. temáticas con una terminología no apropiada. Saber decidir cuál es el procedimiento más oportuno en cada situación. Analizar los informaciones reconocerlas y relaciones. Elaboración correcta representaciones. Saber interpretar correctamente una representación gráfica para expresar un concepto y resaltar las características más relevantes. Verificar conclusiones y realizar inferencias empleando distintas formas de razonamiento. de Conocer las propiedades de las operaciones y aplicarlas correctamente. datos e para descubrir Justificar los diversos pasos de Organizar datos en Ejemplificar procedimientos y un procedimiento. tablas de acuerdo resultados generales. al criterio para que Sistematizar y resumir permita conclusiones realizadas e generalizar los interpretar las ideas resultados. matemáticas presentes en él. Traducir los elementos de un problema de un modo de expresión a otro y argumentar las estrategias más oportunas. Efectuar ampliaciones, generalizaciones y optimizaciones de procedimientos para resolver problemas. La evaluación por competencias en matemáticas se refiere específicamente al “hacer” y tiene en cuenta 3 relaciones: 14.1. En relación con los conceptos: Comprender, reconocer y utilizar el lenguaje técnico-científico propio del área de Matemáticas. Asimilación y aplicación a la práctica de los conceptos trabajados. Conocimiento y utilización de las técnicas de trabajo y razonamiento propias del área. Comprensión y explicación de los problemas planteados, como paso para interpretar la realidad matemática que nos rodea. Aportes e iniciativas en el trabajo tanto de aula como en grupo. 14.2. En relación con los procedimientos: Expresión oral correcta y adecuada. Uso correcto de la simbología matemática y conocimiento de las propiedades a la hora de operar y simplificar expresiones matemáticas. Organización y uso de los materiales adecuados al trabajo que se realice. Presentación de trabajos y cuaderno. Identificación de procedimientos correctos según la intencionalidad Técnicas de trabajo intelectual: subrayado, esquemas, mapas conceptuales... Síntesis y análisis de resultados. Búsqueda y uso de fuentes de información. Planteamiento y resolución de problemas. Sistematización. Formulación y contrastación de hipótesis. Autonomía en el aprendizaje. Explicación de razones para distintas etapas de un procedimiento empleando un lenguaje matemático 14.3. En relación con las actitudes: Atención y participación en clase. Orden y limpieza en los trabajos. Cuidado de los materiales. Interés y curiosidad por la matemática. Respeto y tolerancia hacia los demás. 14.4. Los criterios que tendría en cuenta a la hora de evaluar el aprendizaje de los estudiantes serían los siguientes: Servirá para conocer el nivel de conocimientos del estudiante y tomar medidas en consecuencia. Se llevará a cabo evaluación continua. Se realizarán un mínimo de 2 pruebas escritas, un trabajo en grupo, y varias actividades individuales, además de las observaciones directas en clase tanto del trabajo que se esté realizando con el cuaderno y el texto guía. La calificación se establecerá teniendo en cuenta los aspectos reseñados en el decreto 1290 14.5. Los instrumentos a utilizar en la evaluación del área son: Observación en el aula: Trabajo en aula. Debates. Preguntas y ejercicios en la pizarra. Planteamiento y análisis de ejercicios y problemas. Trabajo en el aula taller. Trabajo en equipo. Cuaderno del alumno: Trabajo independiente. Esquemas, resúmenes, expresión. Planteamiento y análisis de ejercicios y de problemas. Presentación de trabajos en forma ordenada, limpios, sin enmendaduras y respondiendo a los acuerdos grupales. Pruebas objetivas y trabajos individuales o en grupo: Presentación Aplicación de algoritmos Razonamiento Procedimientos 14.6. Por esta razón la evaluación debe tener en cuenta el siguiente proceso: GRÁFICA Nº 1 PROCESO DE LA EVALUACIÓN. PROCESO CONJUNTO DE COMPETENCIAS formato del problema situaciones contexto nociones claves SOLUCION DE PROBLEMAS CONTENIDO La escala de valoración de los desempeños de los estudiantes será cualitativa y numérica. Cualitativa atendiendo a la valoración que define el decreto 1290 en su artículo 5°. Numérica, porque este rango da claridad y permite estandarizar el proceso de evaluación de los estudiantes para la gestión de la calidad institucional, es decir: TABLA Nº 5. Escala de valoración institucional y su equivalencia con la escala nacional. VALORACIÓN RANGO DESCRIPCIÓN Desempeño Superior 4.6 a 5.0 Desempeño metas y que supera expectativas propuestas. Desempeño Alto 4.0 a 4.5 Desempeño por encima de los requerimientos básicos. Desempeño Básico 3.0 a 3. 9 Desempeño mínimo, acorde con los requerimientos básicos fijados por el MEN en sus lineamientos y Estándares. Desempeño Bajo 1.0 a 2.9 Desempeño por debajo de los requerimientos básicos. Requiere de planes de apoyo para superar las debilidades presentadas. Desempeño Superior: alcanza todos los logros esperados e incluso logros no previstos en los Estándares Curriculares y en el Proyecto Educativo Institucional. Adicionalmente cumple con todos los procesos de desarrollo Cognitivo, Psicomotor, Comunicativo, Afectivo y Volitivo, en un desempeño que supera los objetivos y las metas de calidad previstos en el PEI. Se puede considerar con un Desempeño Superior al estudiante que reúna, entre otras las siguientes características: Alcanza la totalidad de los logros propuestos e incluso logros no previstos en los períodos de tiempo asignados. Es creativo, innovador y puntual en la presentación de los trabajos y tareas. Es analítico y crítico en sus puntos de vista. No presenta dificultades en su comportamiento y en el aspecto relacional con todas las personas de la comunidad educativa. Manifiesta sentido de pertenencia institucional. participa en las actividades curriculares y extracurriculares permanentemente. Presenta actitudes de liderazgo y gran capacidad de trabajo en equipo. Desempeño Alto: Corresponde al estudiante que alcanza la totalidad de los logros previstos en cada una de las dimensiones de la formación humana, demostrando un buen nivel de desarrollo. Cuando el estudiante reúna, entre otras, las siguientes características: Alcanza los logros propuestos en las diferentes Áreas / Asignaturas. Tiene faltas de asistencia justificadas no incidentes en su rendimiento. Desarrolla actividades curriculares específicas. Reconoce y supera dificultades de comportamiento cuando las tiene. Manifiesta sentido de pertenencia con la Institución. Desarrolla buena capacidad de trabajo en equipo. Cumple con las tareas y trabajos asignados. Desempeño Básico: Corresponde al estudiante que logra lo mínimo en los procesos de formación aunque con tal estado puede continuar avanzando, hay necesidad de fortalecer su trabajo para que alcance mayores niveles de logro. Se puede considerar desempeño básico cuando el estudiante reúna, entre otras, las siguientes características: Solo alcanza los niveles necesarios de logro propuestos y con Actividades Especiales de Recuperación. Tiene faltas de asistencia justificadas, pero que limitan su proceso de aprendizaje. Presenta algunas dificultades en el aspecto relacional con las personas de su comunidad educativa. Reconoce y supera sus dificultades de comportamiento. Desarrolla actividades curriculares específicas. Utiliza estrategias de apoyo para resolver situaciones pedagógicas pendientes. Su capacidad de trabajo en equipo es limitada. Desempeño Bajo: Corresponde al estudiante que no supera los desempeños necesarios previstos en las Áreas / Asignaturas, teniendo un ejercicio muy limitado en todos los procesos de desarrollo Cognitivo, Psicomotor, Comunicativo, Afectivo y Volitivo, por lo que su desempeño no alcanza los objetivos y las metas de calidad previstos en el PEI. Se puede considerar desempeño bajo cuando el estudiante presente entre otras, las siguientes características: No alcanza los logros mínimos en las Áreas / Asignaturas y requiere Actividades de Apoyo. No alcanza los logros mínimos en las Áreas / Asignaturas y aún después de realizadas las Actividades de Apoyo persiste en las debilidades. Presenta faltas de asistencia injustificadas que afectan significativamente su proceso de aprendizaje. Presenta dificultades de comportamiento. Incumple constantemente con las tareas y trabajos que promueve el área. No demuestra motivación e interés por las actividades escolares. 15. PROYECTOS QUE LIDERA EL ÁREA: Durante el año escolar tuvimos la participación de 4 actividades educativas 3 actividades como participantes y una como organizadores, las actividades fueron: Olimpiadas Departamentales del Conocimiento: Después de un proceso de inscripción con la Gobernación de Antioquia el día martes 15 de Julio los estudiantes de grado Décimo y Undécimo presentaron la primera prueba clasificatoria de las olimpiadas del conocimiento, de 10:00am a 1:30pm, esta prueba se realizó en todo el departamento de Antioquia albergando alrededor de 77 mil estudiantes de los cuales se clasificaron 256 de los mismos para la segunda ronda encontrando dentro de los clasificados a 2 estudiantes del Municipio de Bello, de los Cuales uno de ellos era nuestro el joven Juan diego Mazo estudiante de 11.A, luego este mismo estudiante el 2 de agosto presento la segunda prueba clasificatoria quedando entre 45 participantes el cual concursarían por el valle de aburra y Juan Diego seria representante del municipio de Bello para afrontar las semifinales el 9 de octubre del presente año en las instalaciones de nuestra institución. Olimpiadas Universidad de Antioquia: El proceso de inscripción de estas reconocidas justas fueron entre el 14 de julio y el 2 de agosto del presente año por nuestra institución inscribimos a 15 estudiantes de los grados sexto a once, es de remarcar que estos estudiantes pertenecían a el grupo de altas competencias que se creó este año. El 28 de septiembre se realizó la primera prueba clasificatoria donde estaban inscritos alrededor de 750 estudiantes de Medellín y algunos municipios cercanos, de los 15 estudiantes que inscribió nuestra institución tuvimos la clasificación a la final de dos estudiantes nuestros, Daniel Naranjo del grado 7ª y Juan Fernando Rincón del grado 11C, en la prueba final que se realizó el sábado 11 de octubre quedando entre los 10 primeros lugares de un grupo cada uno de 56 estudiantes preclasificados a la ronda final. I Seminario Taller de Matemáticas Salle Bello: El 21 y 22 de octubre albergamos en nuestra institución 31 instituciones educativas con un consolidado de 156 personas repartidas entre estudiantes y docentes participando en nuestro I seminario Taller de Matemáticas el cual tenía como objetivo principal promover la incursión de nuevas estrategias en la enseñanza de las matemáticas, nuestra institución realizo ponencia la cual fue ejecutada por Juan Diego Mazo, y tuvimos como participantes a este evento a el grupo de altas competencia matemáticas y los grados once en el omite de logística. Foro Municipal de Educación Nacional sobre la Enseñanza de las Matemáticas: Participamos en el foro Municipal de Educación Nacional sobre la “Enseñanza de las Matemáticas”, realizado el 28 de octubre, a este foro asistieron dos estudiantes de grado 11° la personera del colegio Valentina Ramírez Vásquez del grado 11C y Juan Diego Mazo del Grado 11ª. Este foro se enfocó a la exposición de experiencias significativas en matemáticas, y es de resaltar que el colegio ganador se presentó días antes a nuestro seminario de matemáticas con una propuesta que el colegio ya había implementado durante el año (utilización de elementos del aula taller). 16. RECURSOS Tenemos como recurso la utilización del aula taller y todos los elementos que esta lo conforman, se generaron diferentes horarios para los grados de transición a octavo con un horario especifico alcanzando 102 visitas al mes, en el aula taller podemos encontrar los siguientes elementos. CANTIDAD 10 12 14 5 5 1 CAJÓN 1 CAJÓN 1 CAJÓN 9 25 TARROS 2 TARROS 57 15 3 BOLSAS 2 18 PAQUETES 17 3 17 5 IMPLEMENTO/MUEBLE/EQUIPO O MATERIAL GRADUADORES ALGEBRA GEOMÉTRICA MULTICUBOS DEMOSTRACIONES PITAGÓRICAS CUADRATURAS POLIGONALES DUALIDADES REGULARES CUERPOS GEOMÉTRICOS SECCIONES CÓNICAS TABLAS MATEMÁTICAS BLOQUES LÓGICOS FIGURAS GEOMÉTRICAS ÁLGEBRA GEOMÉTRICA PLANAS TRIQUI TRIDIMENSIONAL BLOQUES LÓGICOS ( MATERIAL DOCENTE) PAQUETE DADOS REGLETAS DUALIDADES TORTAS FRACCIONARIAS (MATERIAL DE DOCENTES) TAMGRAN PEQUEÑOS TAMGRAN GRANDES DESCRIPCIÓN BUENOS 2 INCOMPLETOS 1 INCOMPLETO BUENOS BUENOS COMPLETO COMPLETO COMPLETO COMPLETAS COMPLETOS COMPLETOS COMPLETOS 2 MALOS COMPLETOS 1 INCOMPLETO 2 INCOMPLETAS BUENAS COMPLETAS 1 INCOMPLETO COMPLETOS 13 1 1 4 4 2 20 BLOQUE BASE 10 PARQUÉS AJEDRÉZ DOMINÓ FRACCIONES DOMINÓ SUMAS -RESTAS DOMINÓ DIVISIÓN ÁBACOS DE MADERA 20 ÁBACOS DE PASTA 5 CUBOS DE SOMA DE COLORES 8 PENTOMINOS 12 20 12 25 9 1 4 10 9 ESCUADRAS TORTAS FRACCIONARIAS(BOLSAS) MINIARCO (1 A 12 FICHAS) MINIARCO (1 A 24 FICHAS) TORTAS FRACCIONARIOS (TARROS) TRIÁNGULO DE PASCAL COMPÁS REGLAS BOLSAS DE ÁLGEBRA GEOMÉTRICA 10 TORRES HANOI (PEQUEÑAS) 5 30 2 20 1 10 16 48 1 1 4 1 1 1 1 TORRES HANOI (GRANDES) MULTIFICHAS DAMA CHINA GEOPLANO CUADRÍCULA GOEPLANO DOCENTE MUEBLES DE MADERA MESAS SILLAS VIDEO BEAM CON CONTROL MUEBLE DE ALUMINIO BAFLES TABLERO MADERA TABLERO ACRÍLICO TELEVISOR SONY ESCRITORIO DE MADERA- SILLA 17. CRONOGRAMA DE ACTIVIDADES Olimpiadas Departamentales del Conocimiento. Olimpiadas Universidad de Antioquia. II Seminario Taller de Matemáticas Salle Bello. 2 INCOMPLETOS COMPLETO COMPLETO COMPLETOS COMPLETOS COMPLETOS 5 INCOMPLETOS 1 INCOMPLETO 1 MALO 2 INCOMPLETOS 2 INCOMPLETOS Y MALOS BUENAS 4 INCOMPLETAS COMPLETOS COMPLETOS 2 INCOMPLETOS BUEN ESTADO 2 MALOS BUENAS COMPLETAS 1 INCOMPLETA -1 MALA INCOMPLETAS 1 INCOMPLETA BUENOS BUENOS BUENO BUENOS BUENAS 2 RAYADAS BUENAS MALA IMAGEN BUENO SONIDO MALO BUENO BUENO NO SE SABE BUENO Grupo de Altas Competencias Matemáticas. Grupo de fortalecimiento grados 4° y 5°. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO PRIMERO EJES GENERADORES Pensamiento numérico y sistemas numéricos ESTÁNDARES COMPETENCIAS Y Reconozco significados del número en INTERPRETACIÓN diferentes contextos (medición, conteo, REPRESENTACIÓN comparación, codificación, localización entre otros). Diferenciar las figuras geométricas básicas: triángulo, cuadrado, rectángulo y círculo. Conocer los números del 0 al 9, estableciendo correctamente la relación de orden entre estos. Comprender el procedimiento que se sigue en las operaciones de adición y sustracción de números entre 0 y 9, como una analogía del hecho de ganar o perder en diversas situaciones de la vida cotidiana. Definir la decena en términos de la cantidad de unidades a que equivale. Diferenciar las diversas clases de conjuntos, estableciendo relación de pertenencia y no pertenencia entre un elemento y estos. PRIMERO DISCIPLINAS RELEVANTES FORMULACIÓN Y EJECUCIÓN Representar diversas figuras geométricas y crear dibujos a partir de ellas. Aplicar el criterio de relación de orden para cualquier subconjunto de números entre el 0 y el 9. Utilizar estrategias para resolver problemas que requieran de las operaciones de adición y sustracción con números naturales entre 0 y el 9. Representar por medio de dibujos una decena. RAZONAMIENTO Y ARGUMENTACIÓN Apreciar la aplicabilidad, en la cotidianidad, de las formas que se realizan a partir de las figuras geométricas Trabajar grupal e individualmente en la organización u ordenamiento de cualquier subconjunto de números entre 0 y 9. Usar la adición y la sustracción para explicar diversas situaciones de la cotidianidad (ganancia-perdida, aumento-disminución, entre otras). Compartir con los compañeros el manejo del concepto de decena en términos de las unidades Participar en la construcción de diversos conjuntos a partir de la cotidianidad, en los que se evidencie la relación de pertenencia y no pertenencia de un elemento con estos. . Representar diversas clases de conjuntos, mostrando la relación de pertenencia y no pertenencia entre un elemento y estos. INDICADORES DE DESEMPEÑO Realiza seriaciones con dos o más atributos, a partir de la clasificación y la organización de objetos de acuerdo a su forma, longitud y tamaño. CÓDIGO: ANEXOPE1 VERSIÓN: 1 PREGUNTA PROBLEMATIZADORA Cómo resolver ejercicios y problemas matemáticos aplicando las operaciones de suma y resta en el conjunto de los números naturales para modelar situaciones de la vida diaria? Asocia el número en el rango del 0 al 9 con la cantidad de elementos de un conjunto y la pone en práctica. Resuelve problemas sencillos de suma y resta con material concreto y usando los símbolos matemáticos a partir de una situación cotidiana planteada. Reconoce la decena como una colección de 10 elementos. Establece relaciones de pertenencia y no pertenencia entre elementos de un conjunto. PAL PRUEBA EXTERNA ÁMBITOS CONCEPTUALES Números naturales ESTRATEGIAS DIDÁCTICAS Trabajo con material concreto Análisis y resolución de situaciones cotidianas Interpretación de gráficos Ejercicios con operaciones de suma y resta Resolución de pruebas escritas. Resolución de pruebas escritas tipo saber. Trabajo en la plataforma. CONTENIDOS Clasificación Seriación Conjunto Pertenencia y no pertenencia Representación de cantidades del 0 al 9 Recta numérica Suma Resta Decena CRITERIOS DE EVALUACIÓN Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades. sobre las distintas temáticas. Participación en clase. Evaluaciones escritas ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Evaluación escrita. GRADO PRIMERO EJES GENERADORES PERIODO SEGUNDO DISCIPLINAS RELEVANTES CÓDIGO: ANEXOPE1 VERSIÓN: 1 Pensamiento numérico y sistemas numéricos ESTÁNDARES COMPETENCIAS Y Describo, comparo y cuantifico situaciones INTERPRETACIÓN con números en diferentes contextos y con REPRESENTACIÓN diversas representaciones. Conocer los números del 0 al 99, estableciendo correctamente la relación de orden entre estos: Orden del 0 al 9, orden del 10 al 19, orden del 20 al 50 y por último del 51 al 99. Comprender el procedimiento que se sigue en las operaciones de adición y sustracción de números entre 10 y 99, como una analogía del hecho de ganar o perder en diversas situaciones de la vida cotidiana. Identificar las diversas clases de líneas: abiertas, cerradas, horizontales, verticales y poligonales Deducir el concepto de área a partir de figuras geométricas planas. Analizar las cualidades que presentan diversas situaciones, cosas o personas, organizando dicha información en diagramas (barras horizontales o verticales) y FORMULACIÓN Y EJECUCIÓN Aplicar el criterio de relación de orden para cualquier subconjunto de números entre el 0 y el 99. Utilizar estrategias para resolver problemas que requieran de las operaciones de adición y sustracción con números naturales entre 10 y el 99. Diseñar diversas figuras en las que se evidencien las diversas clases líneas: abiertas, cerradas, horizontales, verticales y poligonales Desarrollar métodos para medir el área de una figura geométrica plana. Clasificar y organizar las cualidades que presentan diversas situaciones, cosas o personas en diagramas (barras horizontales o verticales), para una RAZONAMIENTO Y ARGUMENTACIÓN Trabajar grupal e individualmente en la organización u ordenamiento de cualquier subconjunto de números entre 0 y 99. Usar la adición y la sustracción para explicar diversas situaciones de la cotidianidad (ganancia-perdida, aumento-disminución, entre otras). Inventar nuevas figuras en las que se evidencien las diversas clases de líneas: abiertas, cerradas, horizontales, verticales y poligonales. Apreciar la aplicación de los métodos para medir el área de una figura geométrica plana. Admirar la utilidad del uso de diagramas (barras horizontales o verticales) en el entendimiento práctico de la información que se muestra en los medios de comunicación o se toma de la cotidianidad, y que sirve para la toma de decisiones. CÓDIGO: ANEXOPE1 VERSIÓN: 1 reconociendo la variabilidad de dichas cualidades en el tiempo. mejor lectura información. de la INDICADORES DE DESEMPEÑO Asocia la cantidad con el símbolo en el círculo del 10 al 99 y lo aplica en su vida cotidiana. Realiza problemas de adicción y demuestra un mejor desenvolvimiento en el entorno que lo rodea. Resuelve problemas de sustracción que involucren situaciones matemáticas. Comprende conceptos básicos relacionados con la tabulación de datos y analiza diagrama de barras. Reconoce figuras planas asociándolas con objetos de su entorno. Identifica en su entorno líneas poligonales, puntos y líneas y construye diseños y dibujos con ellas. Pal Prueba externa. CÓDIGO: ANEXOPE1 VERSIÓN: 1 PREGUNTA PROBLEMATIZADORA ¿Cómo Desarrollar la capacidad para aplicar procedimientos matemáticos, leyendo, escribiendo y utilizando el valor posicional de cada cifra para abordar el proceso de resolución y formulación de problemas sencillos de la vida cotidiana? ÁMBITOS CONCEPTUALES Números naturales ESTRATEGIAS DIDÁCTICAS Trabajo con material concreto(ábaco) Análisis y resolución de situaciones cotidianas Interpretación de gráficos y tablas. Ejercicios con operaciones de suma y resta Resolución de pruebas escritas tipo saber. Ejercicios de cálculo mental Trabajo en la plataforma CONTENIDOS Decena Descomposición El ábaco Suma (problemas) Resta (problemas) Representación de datos. Diagrama de barras. Líneas Figuras planas CRITERIOS DE EVALUACIÓN Puntualidad en la entrega de trabajosde3l texto guía y del cuaderno, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades sobre las distintas temáticas. Participación en clase. Trabajo en el aula taller Evaluaciones escritas ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Evaluación escrita. GRADO PERIODO PRIMERO EJES GENERADORES Pensamiento numérico y espacial ESTÁNDARES COMPETENCIAS Y Realizo construcciones y diseños utilizando INTERPRETACIÓN cuerpos y figuras geométricas REPRESENTACIÓN tridimensionales y dibujos o figuras Definir la centena en términos geométricas bidimensionales. de las decenas y las unidades. TERCERO DISCIPLINAS RELEVANTES FORMULACIÓN EJECUCIÓN Y Representar por medio de dibujos la centena en RAZONAMIENTO Y ARGUMENTACIÓN Crear maneras de representar las centenas en términos de las decenas y las unidades. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Establecer la relación de orden existente entre los números del 0 al 999; partiendo por los subconjuntos del 0 al 499 y luego del 500 al 999 Comprender el procedimiento que se sigue en las operaciones de adición reagrupando de números entre 10 y 99, como una analogía del hecho de ganar o perder en diversas situaciones de la vida cotidiana. Diferenciar las características de los cuerpos geométricos básicos: cubo, paralelepípedo, cilindro, cono, esfera, y pirámide. términos de la decena y las unidades Representar mediante diversas maneras la relación de orden existente entre algunos números del 0 al 999 Utilizar estrategias para resolver problemas que requieran de las operaciones de adición reagrupando con números naturales entre 10 y el 99. Admirar la lógica existente entre la relación de orden que compete entre los números del 0 al 999. Usar la adición reagrupando para explicar diversas situaciones de la cotidianidad (ganancia-perdida, aumento-disminución, entre otras). Apreciar la aplicabilidad de los cuerpos geométricos en las estructuras arquitectónicas presentes en diversos espacios de la ciudad Construir cuerpos geométricos básicos: cubo, paralelepípedo, cilindro, cono, esfera, y pirámide INDICADORES DE DESEMPEÑO Asocia la cantidad con el símbolo en el rango del 10 al 999 y lo aplica a su vida cotidiana. Comprende el proceso de reagrupación de unidades y decenas y lo aplica en el proceso de sumas. Identifica las características de los cuerpos geométricos básicos: cubo, paralelepípedo, cilindro, cono, esfera, y pirámide Pal Prueba externa. PREGUNTA PROBLEMATIZADORA Cómo identificar e interpretar la información que proporcionan los números presentes en el entorno ÁMBITOS CONCEPTUALES Números naturales Cuerpos geométricos CONTENIDOS La centena Lectura y escritura de números. Operación de sumas reagrupando. Los cuerpos geométricos: cubo, paralelepípedo, cilindro, cono, esfera, y pirámide CÓDIGO: ANEXOPE1 VERSIÓN: 1 utilizando operaciones básicas que pueden ser empleadas para representar situaciones de la vida cotidiana? ESTRATEGIAS DIDÁCTICAS Trabajo con material concreto (ábacos) Análisis y resolución de situaciones cotidianas Ejercicios con operaciones de suma reagrupando Resolución de pruebas escritas tipo SABER. Trabajo en la plataforma. CRITERIOS DE EVALUACIÓN Ubicación de unidades y decenas y centenas en su respectivo cuadro posicional. Responsabilidad a la hora de utilizar el material concreto. Soluciona adecuadamente situaciones cotidianas, teniendo en cuenta la adición reagrupando. Resuelve problemas planteados a partir de gráficos. Puntualidad en la entrega de trabajos del texto guía y del cuaderno Manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades sobre las distintas temáticas. Participación en clase. Trabajo en el aula taller Las figuras planas ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Evaluación escrita. GRADO PERIODO PRIMERO EJES GENERADORES Pensamiento numérico y sistemas numéricos ESTÁNDARES COMPETENCIAS Y Describo, comparo y cuántico situaciones INTERPRETACIÓN con números en diferentes contextos y con REPRESENTACIÓN diversas representaciones. Comprender el procedimiento que se sigue en las operaciones de adición y sustracción de números entre 100 y 9.999, como una analogía del hecho de ganar o perder en diversas situaciones de la vida cotidiana. CUARTO DISCIPLINAS RELEVANTES FORMULACIÓN EJECUCIÓN Y Utilizar estrategias para resolver problemas que requieran de las operaciones de adición y sustracción con números naturales entre 100 y el 9.999. Utilizar estrategias para resolver problemas que RAZONAMIENTO Y ARGUMENTACIÓN Usar la adición y la sustracción para explicar diversas situaciones de la cotidianidad (ganancia-perdida, aumento-disminución, entre otras). Usar la sustracción desagrupando para explicar diversas situaciones de la cotidianidad (ganancia-perdida, aumentodisminución, entre otras). CÓDIGO: ANEXOPE1 VERSIÓN: 1 Comprender el procedimiento que se sigue en las operaciones de sustracción desagrupando de números entre 10 y 99, como una analogía del hecho de ganar o perder en diversas situaciones de la vida cotidiana. Comprender la manera de leer el reloj y el calendario Evaluar la probabilidad de ocurrencia de un evento: evento seguro o imposible, evento muy probable o poco probable. PREGUNTA PROBLEMATIZADORA Cómo identificar e interpretar la información que proporcionan los números presentes en el entorno utilizando operaciones básicas que pueden ser empleadas para representar requieran de las operaciones de sustracción desagrupando con números naturales entre 10 y el 99. Leer el reloj calendario correctamente y Aceptar la funcionalidad del reloj y el calendario en las actividades humanas. Diseñar situaciones en las que se pueda medir la probabilidad de ocurrencia de un evento. el Expresar la probabilidad de ocurrencia de un evento: evento seguro o imposible, evento muy probable o poco probable, a partir de una situación planteada. INDICADORES DE DESEMPEÑO Asocia la cantidad con el símbolo en el rango del 100 al 9.999 y lo aplica a su vida cotidiana. Comprende el proceso de desagrupación y lo aplica en la solución de restas. Reconoce el reloj como instrumento para medir el tiempo de duración de algunos eventos a través de la experimentación y el juego Identifica situaciones en las que se pueda medir la probabilidad de ocurrencia de un evento. Halla la cantidad desconocida en problemas elementales de la vida cotidiana. PAL PRUEBA EXTERNA ÁMBITOS CONTENIDOS CONCEPTUALES Números naturales Unidad de mil Restas desagrupando Medidas de tiempo Probabilidad Solución de problemas Antes y después El tiempo CÓDIGO: ANEXOPE1 VERSIÓN: 1 situaciones cotidiana? de la vida ESTRATEGIAS DIDÁCTICAS Trabajo con material concreto y ábacos. Análisis y resolución de situaciones cotidianas Ejercicios con operaciones de resta desagrupando Resolución de pruebas escritas tipo SABER. Trabajo en la plataforma Concepto de multiplicación con material concreto (regletas) CRITERIOS DE EVALUACIÓN Responsabilidad a la hora de utilizar el material concreto. Soluciona adecuadamente situaciones cotidianas, teniendo en cuenta la sustracción desagrupando. Resuelve problemas planteados a partir de gráficos. Puntualidad en la entrega de trabajos del texto guía y del cuaderno Manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades sobre las distintas temáticas. Participación en clase. Trabajo en el aula taller ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Evaluación escrita. GRADO PERIODO SEGUNDO EJES GENERADORES Pensamiento numérico y sistemas numéricos ESTÁNDARES COMPETENCIAS Y Describo, comparo y cuantifico situaciones INTERPRETACIÓN con números en diferentes contextos y con REPRESENTACIÓN diversas representaciones. Relacionar los números naturales hasta 999 mediante las operaciones de adición y sustracción, reagrupando y desagrupando unidades y decenas. Establecer la relación de orden existente entre los números del 0 al 999; partiendo por los subconjuntos del 0 al 499 y luego del 500 al 999 Diferenciar las diversas clases de conjuntos, estableciendo PRIMERO DISCIPLINAS RELEVANTES FORMULACIÓN Y EJECUCIÓN Utilizar estrategias para resolver problemas que requieran de las operaciones de adición y sustracción con números naturales entre 0 y el 999. Representar mediante diversas maneras la relación de orden existente entre algunos números del 0 al 999. RAZONAMIENTO Y ARGUMENTACIÓN Usar la adición y la sustracción para explicar diversas situaciones de la cotidianidad (ganancia-perdida, aumento-disminución, entre otras). Admirar la lógica existente entre la relación de orden que compete entre los números del 0 al 999. Participar en la construcción de diversos conjuntos a partir de la cotidianidad, en los que se evidencie la relación de pertenencia y no pertenencia de un elemento con estos. CÓDIGO: ANEXOPE1 VERSIÓN: 1 relación de pertenencia y no pertenencia entre un elemento y estos. Definir el concepto de volumen de un cuerpo geométrico. Representar diversas clases de conjuntos, mostrando la relación de pertenencia y no pertenencia entre un elemento y estos. Preferir una estrategia sobre otra a la hora de medir el volumen de un cuerpo geométrico, demostrando practicidad en dicha elección. Desarrollar estrategias para medir el volumen de un cuerpo geométrico. INDICADORES DE DESEMPEÑO Utiliza el proceso de la adición reagrupando en la solución de problemas matemáticos en contextos cotidianos. Soluciona problemas de sustracciones desagrupando a partir de enunciados matemáticos en contextos cotidianos Compone y descompone números hasta el 999 y halla su respectivo valor posicional Representa en forma concreta y grafica conjuntos de elementos con diferentes características Reconoce diferentes tipos de cuerpos geométricos. PAL PRUEBA EXTERNA PREGUNTA PROBLEMATIZADORA ¿ Cómo Desarrollar la capacidad para aplicar procedimientos matemáticos, leyendo, escribiendo y utilizando el valor posicional de cada cifra para abordar el proceso de resolución y formulación de problemas sencillos? ESTRATEGIAS DIDÁCTICAS ÁMBITOS CONCEPTUALES Números naturales CONTENIDOS Adición y sustracción de los números en el rango del 0 al 999. Términos de la adición. Adiciones reagrupando Términos de la sustracción. Sustracciones sencillas y desagrupando. Características de un conjunto Representación de un conjunto. Cardinal de un conjunto Relación de pertenencia Símbolos de relación de pertenencia. Subconjuntos CRITERIOS DE EVALUACIÓN CÓDIGO: ANEXOPE1 VERSIÓN: 1 Trabajo con material concreto Análisis y resolución de situaciones cotidianas Interpretación de gráficos Ejercicios con operaciones de suma y resta Resolución de pruebas escritas. Lectura de gráficos. Resolución de pruebas escritas tipo saber. Trabajo en la plataforma. Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades sobre las distintas temáticas. Participación en clase. Evaluaciones escritas. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Evaluación escrita. GRADO PERIODO SEGUNDO EJES GENERADORES Pensamiento numérico y Geométrico-métrico. ESTÁNDARES COMPETENCIAS Y Construyo secuencias numéricas INTERPRETACIÓN y geométricas utilizando propiedades de los REPRESENTACIÓN números y de las figuras Reconocer los números hasta geométricas 99.999, definiendo las unidades de mil, y la estructura de los números de cuatro cifras y cinco cifras. Establecer la relación de orden de números hasta de cinco cifras. Comprobar la probabilidad de que ocurra un evento. Expresar un conjunto de datos mediante una tabla de frecuencia, diagrama de barras o pictogramas. SEGUNDO DISCIPLINAS RELEVANTES FORMULACIÓN Y EJECUCIÓN Leer y escribir números pertenecientes al subconjunto del 0 al 99.999 Plantear situaciones en las que la ocurrencia de un evento sea muy o poco probable. Representar la información de una tabla de frecuencia mediante un diagrama de barras o un pictograma. RAZONAMIENTO Y ARGUMENTACIÓN Organizar números pertenecientes subconjunto del 0 al 99.999 al Usar las propiedades de la probabilidad en situaciones de la vida cotidiana que se relacionen con eventos aleatorios. Representar la información de una tabla de frecuencia mediante un diagrama de barras o un pictograma. Interesarse por representar productos entre números naturales mediante adición de conjuntos, entendiendo que este es el punto de partida para entender la razón de la operación de multiplicación de números. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Comprender la operación de la multiplicación de números naturales, como la suma de conjuntos con igual cantidad de elementos. Representar productos entre números naturales como la adición de conjuntos con igual cantidad de elementos. Diseñar dibujos con las diferentes clases de líneas, resaltando las características de cada una de estas. Identificar y reconocer las diferentes clases de líneas. Trazar figuras empleando las diferentes clases de líneas. INDICADORES DE DESEMPEÑO Resuelve operaciones matemáticas en situaciones cotidianas, que se le presentan, con los números naturales en el rango de 0 al 99.999 Identifica el valor posicional de los números del 0 al 99.999. Maneja adecuadamente los elementos básicos de la estadística y probabilidad(tabla de frecuencia, pictogramas, probabilidad) Utiliza el proceso de la adición reagrupando en la solución de problemas matemáticos en contextos cotidianos hasta el 99.999 Soluciona problemas de sustracciones desagrupando a partir de enunciados matemáticos en contextos cotidianos hasta el 99.999 Reconoce con claridad la multiplicación como una adición de sumandos iguales Ilustra figuras empleando las diferentes clases de líneas. Pal Prueba externa. PREGUNTA PROBLEMATIZADORA ¿Cómo Describir, comparar y cuantificar situaciones con números en diferentes contextos y con diversas representaciones? ÁMBITOS CONCEPTUALES Números naturales CONTENIDOS Unidades de mil Decenas de mil Adición y sustracción de los números en el rango del 0 al 99.999 Los cuerpos geométricos Caras y vértices de los cuerpos geométricos Cubo, cono, cilindro y esfera. Líneas Tablas de frecuencia Barras de diagramas CÓDIGO: ANEXOPE1 VERSIÓN: 1 Adiciones y sustracciones hasta el 99.999 Adición de sumandos iguales ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Trabajo con material concreto(ábaco) Puntualidad en la entrega de trabajos del texto guía y del cuaderno, manejo del tiempo dentro y Análisis y resolución de situaciones cotidianas fuera del salón de clase en el desarrollo de las actividades sobre las distintas temáticas. Interpretación de gráficos y tablas. Participación en clase. Ejercicios con operaciones de suma reagrupando y Trabajo en el aula taller resta desagrupando. Evaluaciones escritas Resolución de pruebas escritas tipo saber. Ejercicios de cálculo mental Trabajo en la plataforma ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Evaluación escrita. GRADO PERIODO SEGUNDO TERCERO EJES GENERADORES DISCIPLINAS RELEVANTES Pensamiento numérico y espacial ESTÁNDARES COMPETENCIAS Y FORMULACIÓN Y RAZONAMIENTO Y ARGUMENTACIÓN Reconocer el efecto que tienen las INTERPRETACIÓN EJECUCIÓN operaciones básicas (suma, resta, REPRESENTACIÓN multiplicación y división) sobre los números. Comprender la operación de la Interesarse por representar productos entre multiplicación de números Representar productos números naturales mediante adición de naturales, como la suma de entre números naturales conjuntos, entendiendo que este es el punto conjuntos con igual cantidad de como la adición de de partida para entender la razón de la conjuntos con igual operación de multiplicación de números. elementos. cantidad de elementos. Conocer la multiplicación y sus Apreciar el significado de la multiplicación de Resolver términos. números entre el 0 y el 9, como un medio de multiplicaciones entre abreviar el proceso de adición. Reconocer las características y números del 0 al 9. elementos de las figuras Crear dibujos a partir de las figuras planas: planas: rectángulo, triángulo y Representar y clasificar rectángulo, triángulo y círculo. las diferentes figuras círculo. planas: rectángulo, Mostar claridad a la hora de asignar unidades Definir y distinguir las unidades triángulo y círculo. de medida a una longitud medida. de medida para longitudes: centímetro, decímetro y metro. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Medir longitudes, entre estos perímetros, asignando correctamente las unidades de medida. INDICADORES DE DESEMPEÑO Reconoce, con claridad, la multiplicación como una adición de sumandos iguales. Identifica, correctamente, el operador y los términos de una multiplicación. Plantea y resuelve, con exactitud, situaciones multiplicativas. Identifica figuras planas en diferentes contextos. Estima la longitud de un objeto en metros, centímetros o decímetros. ÁMBITOS CONTENIDOS CONCEPTUALES Números naturales Adición de sumandos iguales. Figuras planas. Adición y multiplicación. Multiplicación con las tablas del 1 al 9 Multiplicación por una cifra Figuras planas Metro, centímetro y decímetro. PREGUNTA PROBLEMATIZADORA Cómo identificar e interpretar la información que proporcionan los números presentes en el entorno utilizando operaciones básicas que pueden ser empleadas para representar situaciones de la vida cotidiana? ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Trabajo con material concreto ( regletas) Responsabilidad a la hora de utilizar el material concreto. Análisis y resolución de situaciones cotidianas Soluciona adecuadamente situaciones cotidianas, teniendo en cuenta la multiplicación Ejercicios con operaciones de multiplicación Puntualidad en la entrega de trabajos del texto guía y del cuaderno Lectura de gráficos. Manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades sobre Ejercicios de experimentación con el metro. las distintas temáticas. Resolución de pruebas escritas tipo SABER. Participación en clase. Trabajo en la plataforma. Trabajo en el aula taller ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Evaluación escrita. GRADO PERIODO SEGUNDO CUARTO EJES GENERADORES DISCIPLINAS RELEVANTES CÓDIGO: ANEXOPE1 VERSIÓN: 1 Pensamiento numérico y sistemas numéricos ESTÁNDARES COMPETENCIAS Y Describo, comparo y cuántico situaciones INTERPRETACIÓN con números en diferentes contextos y con REPRESENTACIÓN diversas representaciones. Analizar relaciones de semejanza, congruencia y simetría entre figuras planas. Describir los algoritmos que se deben seguir en las operaciones básicas (suma, resta multiplicación) con números de dos cifras Deducir el concepto de área para una figura plana. Expresar la división por medio de repartos exactos e inexactos. PREGUNTA PROBLEMATIZADORA Cómo identificar e interpretar la información que proporcionan los números presentes en el entorno utilizando operaciones básicas que pueden ser FORMULACIÓN Y EJECUCIÓN Clasificar pares o conjuntos de figuras geométricas planas como congruentes, semejantes o simétricas. Efectuar adiciones, sustracciones y multiplicaciones con números de dos cifras. Utilizar cuadrados y triángulos para hallar el área de una figura plana. RAZONAMIENTO Y ARGUMENTACIÓN Admirar la relación de congruencia entre pares o conjuntos de figuras geométricas planas. Interiorizar los procesos de adición, sustracción y multiplicación en el conjunto de los naturales Inventar maneras alternativas para medir el área de una figura plana Participar en la realización de los repartos exactos e inexactos, para entender la operación de la división en el conjunto de los números naturales Realizar repartos exactos e inexactos. INDICADORES DE DESEMPEÑO Identificar cuando dos figuras son congruentes o semejantes Realizar multiplicaciones por dos cifras Identifica los lados y vértices de algunas figuras planas. Resuelve divisiones exactas e inexactas de manera simbólica y concreta, por una cifra, por dos o tres cifras en el dividendo. PAL PRUEBA EXTERNA ÁMBITOS CONTENIDOS CONCEPTUALES Números naturales Congruencia y semejanza La multiplicación por dos cifras Figuras planas La división CÓDIGO: ANEXOPE1 VERSIÓN: 1 empleadas para representar situaciones de la vida cotidiana? ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Responsabilidad a la hora de utilizar el material concreto. Trabajo con material concreto y ábacos. Soluciona adecuadamente situaciones cotidianas, teniendo en cuenta la sustracción Análisis y resolución de situaciones cotidianas desagrupando. Ejercicios con figuras. Resuelve problemas planteados a partir de gráficos. Resolución de pruebas escritas tipo SABER. Puntualidad en la entrega de trabajos del texto guía y del cuaderno Trabajo en la plataforma Manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades sobre las distintas temáticas. Participación en clase. Trabajo en el aula taller. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Evaluación escrita. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO TERCERO EJES GENERADORES Pensamiento numérico – aleatorio – métrico. ESTÁNDARES Expresa sus ideas en forma clara. Interpreta, representa y utiliza diferentes tipos de lenguaje para describir relaciones entre los números. Uso diversas estrategias de cálculo (especialmente cálculo mental) y de estimación para resolver problemas en situaciones aditivas. Reconozco nociones de horizontalidad, verticalidad, paralelismo y perpendicularidad en distintos contextos y su condición relativa con respecto a diferentes sistemas de referencia. Clasifico y organizo datos de acuerdo a cualidades y atributos y los presento en tablas. PERIODO PRIMERO DISCIPLINAS RELEVANTES COMPETENCIAS INTERPRETACIÓN Y REPRESENTACIÓN Clasifico y reconozco elementos de un conjunto de acuerdo con características comunes. Interpreto y analizo diferentes situaciones problema en donde se usan operaciones aditivas (adición y sustracción). Razonar sobre las condiciones necesarias para que dos rectas sean consideradas paralelas o pediculares y diferenciar entre el concepto de recta y de segmento de recta. Reconocer los submúltiplos de la unidad patrón metro más utilizado en la medición de longitudes (centímetro y decímetro). Organiza y representa elementos básicos de conjunto de datos. los un FORMULACIÓN Y EJECUCIÓN Resuelvo problemas que involucren más de una operación, ordenando los números de mayor a menor orden relacionando un número de seis cifras con la cantidad que representa. RAZONAMIENTO Y ARGUMENTACIÓN Asumo una posición activa en la solución de problemas que involucran conjuntos Aceptar la amplia aplicabilidad de las operaciones de adición y sustracción, para los números hasta 999999, en la vida cotidianidad. Formula y justifica los procedimientos afines a las propiedades de la adición y términos de la sustracción. Mencionar estructuras o partes de estas en las que sea importante aplicar el concepto de paralelismo y perpendicularidad. Graficar rectas paralelas o pediculares, mostrando claramente las características de cada par de rectas. Apreciar la importancia de que existan unidades de medida estandarizadas como el metro y sus submúltiplos para medir los objetos que nos rodean. Medir el largo, el ancho, el alto, el perímetro u otras características de un objeto tridimensional; tomando como referencia los submúltiplos de la unidad patrón metro: centímetro y decímetro. Construir y/o adaptar la información que nos brinda el entorno escolar o barrial a Analizar e interpretar los datos o información que el entorno escolar o barrial nos brinda, a la luz de los criterios de clasificación de variables; para luego consignarla en una tabla de frecuencias. CÓDIGO: ANEXOPE1 VERSIÓN: 1 objetos concretos, diagramas de barras. PREGUNTA PROBLEMATIZADORA INDICADORES DE DESEMPEÑO Reconocer y resolver operaciones entre conjuntos. Identificar el valor y la posición de cada dígito en números hasta 99 999. Efectuar operaciones de adición y sustracción para los números naturales hasta 999999, señalando los términos y diciendo las propiedades que se aplican para estos números. Establece diferencias entre recta paralela y recta perpendicular. Mide y compara medidas de objetos. Realiza conversiones de centímetros a decímetros. Resuelve situaciones en las cuales se usan las unidades de medida y conversiones pertinentes. ÁMBITOS CONTENIDOS CONCEPTUALES Conjuntos, Sistemas Representación y determinación de conjuntos de numeración, recta, Relaciones y operaciones entre conjuntos segmento, unidades Adición y términos de la adición hasta 999.999 de medida. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Propiedades de la adición. Sustracción y términos de la sustracción. Recta y semirrecta. Rectas paralelas y perpendiculares. Segmento. Unidades de Medida. Variables cualitativas y cuantitativas. Tablas de Frecuencia. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Análisis de imágenes Participación en clase. Aula taller de Matemáticas Cuaderno (Toma de nota en clase). Trabajos a partir de presentaciones video gráficas. Presentación de Trabajos de manera individual o grupal. Socializaciones de las temáticas. Claridad y coherencia frente a la participación en la solución de conjuntos Participación en clase. Capacidad de argumentar claramente en cada una de las actividades realizadas. Ejercicios en clase y casa del texto guía. Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en Resolución de pruebas escritas el desarrollo de las actividades. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Ejercicios de profundización sobre conjuntos, propiedades y relaciones GRADO PERIODO TERCERO EJES GENERADORES Pensamiento numérico – métrico – aleatorio. ESTÁNDARES COMPETENCIAS Usar diversas estrategias de cálculo INTERPRETACIÓN (especialmente cálculo mental) y de REPRESENTACIÓN SEGUNDO DISCIPLINAS RELEVANTES Matemática operativa básica Y FORMULACIÓN Y EJECUCIÓN RAZONAMIENTO ARGUMENTACIÓN Y CÓDIGO: ANEXOPE1 VERSIÓN: 1 estimación para resolver problemas en situaciones aditivas y multiplicativas. Utilizo los números romanos para expresar cantidades. Expresa cantidades en números romanos y viceversa. Reconozco congruencia y semejanza entre figuras (ampliar, reducir). Conocer y enumerar las propiedades de la multiplicación, reconociendo los múltiplos de un número y la manera de abreviarla. Efectuar multiplicaciones entre números de una, dos y tres cifras aplicando las distintas propiedades de esta, para la solución de problemas referentes a la cotidianidad. Examina, analiza e integra las distintas propiedades de la multiplicación y compara los resultados con sus compañeros. Definir conceptual y gráficamente un ángulo y un polígono. Relacionar polígonos regulares e irregulares a partir de criterios de semejanza y congruencias. Construir ángulos y polígonos, mostrando gráficamente criterios de semejanza y congruencia. Participar activamente en la construcción de ángulos y polígonos, mostrando gráficamente criterios de semejanza y congruencia. Preferir una manera particular de representar un conjunto de datos que facilite el entendimiento de estos y la fácil identificación de la moda. Reescribe diagramas y establece rangos frente situaciones o eventos de su vida escolar. Realizo construcciones y diseños utilizando cuerpos y figuras geométricas tridimensionales y dibujos o figuras geométricas bidimensionales. Interpreta la información que nos brinda el entorno escolar o barrial a objetos concretos, pictogramas o diagramas de barras; identificando a parir de estos la moda de los datos. PREGUNTA PROBLEMATIZADORA Justifica estrategias y caminos propuestos para la solución de situaciones problemas. INDICADORES DE DESEMPEÑO Reconocer las cantidades que representan los números romanos. Aplica las propiedades de la multiplicación. Plantea y resuelve situaciones multiplicativas. Clasifica polígonos según su número de lados. Identifica congruencia entre dos polígonos. Representa datos en diagramas de barras. Encuentra la moda en un conjunto de datos. ÁMBITOS CONTENIDOS CONCEPTUALES Números romanos. Números Romanos Multiplicación y términos, propiedades de la multiplicación. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Multiplicación y sus términos. Múltiplos de un número. Polígonos. Diagrama de barras. Moda. CRITERIOS DE EVALUACIÓN Participación en clase. Cuaderno (Toma de nota en clase). Presentación de Trabajos de manera individual o grupal. Capacidad de argumentar claramente en cada una de las actividades realizadas. Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades. ESTRATEGIAS DIDÁCTICAS Análisis de imágenes Trabajos a partir de presentaciones video gráficas. Socializaciones de las temáticas. Participación en clase. Actividad lúdica en patio superior Ejercicios en clase y casa del texto guía. Resolución de pruebas escritas ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Ejercicios de profundización durante la hora de clase con participación activa. GRADO PERIODO TERCERO EJES GENERADORES Pensamiento numérico – métrico – variacional. ESTÁNDARES COMPETENCIAS Reconocer el efecto que tienen las INTERPRETACIÓN operaciones básicas (suma, resta, REPRESENTACIÓN TERCERO DISCIPLINAS RELEVANTES Matemática operativa básica y geométrica Y FORMULACIÓN Y EJECUCIÓN RAZONAMIENTO ARGUMENTACIÓN Y CÓDIGO: ANEXOPE1 VERSIÓN: 1 multiplicación números. y división) sobre los Dibujo y describo cuerpos o figuras tridimensionales en distintas posiciones y tamaños. Realizo construcciones y diseños utilizando cuerpos y figuras geométricas tridimensionales y dibujos o figuras geométricas bidimensionales. Explico –desde mi experiencia– la posibilidad o imposibilidad de ocurrencia de eventos cotidianos. Predigo si la posibilidad de ocurrencia de un evento es mayor que la de otro. PREGUNTA PROBLEMATIZADORA Deducir y relacionar la operación de la división con la de la multiplicación, determinando los divisores de un número y aplicando correctamente el algoritmo de esta. Observar las analogías que se presentan entre la operación de la división y la de multiplicación, para elaborar estrategias de solución a problemas en los que haya que realizar algún tipo de reparto. Describir las características de figuras tridimensionales como el cubo, el paralelepípedo, el prisma y la pirámide, resaltando las maneras de nominarlas de acuerdo a estas. Construir y clasificar figuras tridimensionales en cubo, paralelepípedo, prisma y pirámide de acuerdo a las características de estas y nominarlas correctamente. Enumerar y determinar la cantidad de posibilidades de que ocurra un evento utilizando un diagrama de árbol, el principio de multiplicación, combinaciones ver mutaciones; para así estimar la probabilidad de que ocurra el mismo. Calcular la probabilidad de que ocurra un evento realizando diagramas de árbol, combinaciones y permutaciones para determinar la cantidad de posibilidades de que ocurra dicho evento, y el principio de probabilidad para calcular la misma. Apreciar la funcionalidad que tiene conocer las propiedades y los algoritmos de la división y de la multiplicación para la explicación de diversas cifras o cantidades de la cotidianidad. Diseñar estructuras en las que evidencie el uso y funcionalidad figuras como el cubo, paralelepípedo, el prisma y pirámide. se de el la Aceptar la importancia y aplicabilidad del estudio de la probabilidad de un evento, como un soporte para la toma de decisiones que pueden afectar a todos los miembros de la sociedad. INDICADORES DE DESEMPEÑO Plantea y resuelve, con precisión la división para su solución. Determina, con exactitud, los divisores de un número. Reconoce los poliedros en objetos del entorno. Identifica los elementos de los cuerpos geométricos. Representa información en diagramas de árbol. Responde preguntas a partir de la información presentada en diagramas de árbol. ÁMBITOS CONTENIDOS CONCEPTUALES División. División exacta y términos de la división. División Inexacta. Criterios de Divisibilidad. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Números primos. Cubo. Paralelepípedo. Prisma. Pirámide. Diagrama de árbol. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Análisis de imágenes Participación en clase. Trabajos a partir de presentaciones video gráficas. Cuaderno (Toma de nota en clase). Socializaciones de las temáticas. Presentación de Trabajos de manera individual o grupal. Participación en clase. Claridad y coherencia frente a la participación en la solución de elementos geométricos y Ejercicios en clase y casa del texto guía. multiplicaciones. Resolución de pruebas escritas Capacidad de argumentar claramente en cada una de las actividades realizadas. Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Ejercicios de profundización sobre geometría y multiplicaciones, propiedades y relaciones GRADO TERCERO EJES GENERADORES Pensamiento Numérico - métrico – aleatorio ESTÁNDARES COMPETENCIAS PERIODO CUARTO DISCIPLINAS RELEVANTES CÓDIGO: ANEXOPE1 VERSIÓN: 1 Interpreto las fracciones en diferentes contextos: situaciones de medición, relaciones parte todo, cociente, razones y proporciones. Reconozco y aplico traslaciones y giros sobre una figura. Reconozco y valoro simetrías en distintos aspectos del arte y el diseño. Conjeturo y pongo a prueba predicciones acerca de la posibilidad de ocurrencia de eventos. INTERPRETACIÓN Y REPRESENTACIÓN Definir el concepto de fracción a partir de un conjunto y de la partición de la unidad, especificando los términos que la componen y las clases de fracciones que existen. Representar fracciones especificando los términos de estas y la clase de fracciones que son. Distinguir los movimientos que se pueden realizar con una figura geométrica: reflexión y traslación, y las características que se generan a partir de estos: simetrías. Interpretar el concepto de probabilidad, resaltando su aplicabilidad en algunas situaciones de la vida cotidiana o actividades económicas específicas. PREGUNTA PROBLEMATIZADORA FORMULACIÓN Y EJECUCIÓN Comprobar y describir los pasos que se siguen para la adición y sustracción de fracciones con igual denominador. Efectuar operaciones de adición y sustracción de fracciones con igual denominador, analítica y gráficamente. Manipular figuras geométricas (Reflexiones y traslaciones) de tal manera que podamos observar las características que se suscitan a partir de estas (Simetrías). Expresar numéricamente la probabilidad de un evento. Resolver problemas que involucran el cálculo de una probabilidad. RAZONAMIENTO ARGUMENTACIÓN Y Mostrar la fracción de un conjunto y de la unidad. Utilizando material concreto. Explicar los pasos para sumar o restar fracciones con igual denominador, analítica y gráficamente. Participar en la manipulación de figuras geométricas (Reflexiones y traslaciones) para constatar simetrías o asimetrías. Aceptar la amplia incidencia que tiene el marco teórico que se refiere a la probabilidad de ocurrencia de eventos, en múltiples decisiones que afectan a una persona o a la comunidad. INDICADORES DE DESEMPEÑO Reconoce y representa, correctamente, fracciones. Resuelve, con precisión, operaciones aditivas con números fraccionarios. Realiza con claridad movimientos de figuras planas. Realiza construcciones de mosaicos. Establece la posibilidad de ocurrencia de un evento. ÁMBITOS CONTENIDOS CONCEPTUALES CÓDIGO: ANEXOPE1 VERSIÓN: 1 Términos de una fracción. Fracciones equivalentes. Fracciones homogéneas y heterogéneas. Adición y sustracción de fracciones. Multiplicación de fracciones. Reflexión, simetría, traslación. Principio de probabilidad. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Análisis de imágenes Participación en clase. Trabajos a partir de presentaciones video gráficas. Cuaderno (Toma de nota en clase). Socializaciones de las temáticas. Presentación de Trabajos de manera individual o grupal. Elaboración de carteleras Claridad y coherencia frente a la participación en la solución de inecuaciones. Ejercicios de consulta. Capacidad de argumentar claramente en cada una de las actividades realizadas. Resolución de pruebas escritas Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Fracciones, Transformaciones Isométricas, Probabilidad. GRADO PERIODO CUARTO EJES GENERADORES Pensamiento numérico - métrico – aleatorio ESTÁNDARES COMPETENCIAS PRIMERO DISCIPLINAS RELEVANTES Matemática operativa básica CÓDIGO: ANEXOPE1 VERSIÓN: 1 Describo, comparo y cuantifico situaciones con números, en diferentes contextos y con diversas representaciones. Comparar y clasificar figuras bidimensionales de acuerdo a sus componentes (ángulos, vértices) y sus características. Reconozco nociones de horizontalidad, verticalidad, paralelismo y perpendicularidad en distintos contextos y su condición relativa con respecto a diferentes sistemas de referencia. Describo e interpreto representadas en gráficos. variaciones INTERPRETACIÓN Y REPRESENTACIÓN Conocer las operaciones básicas que cumplan con las propiedades para los números naturales. Identificar los polígonos regulares de acuerdo al número de ángulos interiores. Reconocer las características de las rectas paralelas y perpendiculares. Analizar la información que se presenta por medio de gráficas. FORMULACIÓN Y EJECUCIÓN Resolver operaciones básicas que cumplan con las propiedades para los números naturales. RAZONAMIENTO Y ARGUMENTACIÓN Participar en la solución de problemas y ejercicios utilizando las operaciones básicas para los números naturales. Clasificar y construir los polígonos regulares de acuerdo al número de ángulos interiores. Analiza las actividades clasificación y construcción polígonos regulares. Representar rectas paralelas y perpendiculares. Disfrutar en la representación y trazado de rectas paralelas y perpendiculares. Representar datos usando tablas y representación gráfica. de de Diseñar algún tipo de representación gráfica para organizar los datos presentados en una situación problema. INDICADORES DE DESEMPEÑO Reconocer y resolver operaciones entre conjuntos. Resuelve operaciones combinadas de adición y sustracción siguiendo el orden de las operaciones. Identifica propiedades de la adición y de la multiplicación. Aplica correctamente el algoritmo de la división. PREGUNTA ÁMBITOS CONTENIDOS PROBLEMATIZADORA CONCEPTUALES Sistemas de Lectura, escritura y orden de números naturales. numeración, Operaciones combinadas de adición y sustracción. Propiedades de la adición y multiplicación. Operaciones combinadas Relación entre la adición y la multiplicación. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Análisis de imágenes Participación en clase. Aula taller de Matemáticas Cuaderno (Toma de nota en clase). CÓDIGO: ANEXOPE1 VERSIÓN: 1 Trabajos a partir de presentaciones video gráficas. Presentación de Trabajos de manera individual o grupal. Socializaciones de las temáticas. Claridad y coherencia frente a la participación en la solución de conjuntos Participación en clase. Capacidad de argumentar claramente en cada una de las actividades realizadas. Ejercicios en clase y casa del texto guía. Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en Resolución de pruebas escritas el desarrollo de las actividades. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Ejercicios de profundización sobre conjuntos, propiedades y relaciones, Ejercicios de profundización durante la hora de clase con participación activa. GRADO CUARTO EJES GENERADORES Pensamiento numérico – métrico – aleatorio. ESTÁNDARES Usar diversas estrategias de cálculo y de estimación para resolver problemas en situaciones aditivas y multiplicativas. Comparo y clasifico figuras bidimensionales de acuerdo con sus componentes (ángulos, vértices) y características. Describo situaciones o eventos a partir de un conjunto de datos. PERIODO SEGUNDO DISCIPLINAS RELEVANTES Matemática operativa básica y geométrica COMPETENCIAS INTERPRETACIÓN Y REPRESENTACIÓN Reconozco características del conjunto de múltiplos de un número natural. Memorizar las fórmulas para hallar el área y el perímetro de figuras planas. Establecer diferencias entre el círculo y la circunferencia especificando sus elementos (radio, diámetro, cuerdas y ángulos). Deducir las medidas de tendencia central (moda, media y mediana) de un conjunto de datos tomados de una encuesta. FORMULACIÓN Y EJECUCIÓN Aplicar propiedades de la multiplicación en la solución de operaciones. Relaciona características de multiplicidad y divisibilidad de los números 2, 3, 6, 5 y 10. Usar las fórmulas para hallar el perímetro y el área de las figuras planas. Utilizar el transportador para medir y construir ángulos, además, del compás, para hacer circunferencias. Utilizar las medidas de tendencia central para analizar los RAZONAMIENTO Y ARGUMENTACIÓN Asumo una posición activa en la solución de problemas que involucran propiedades de la multiplicación. Encuentro otras fuentes que trabajen la divisibilidad. Colaborar con la ejecución de las actividades para la buena comprensión de las formulas. Participar activamente en la medición y construcción de ángulos y circunferencias. Inventar encuestas que me lleven a indagar acerca de los gustos de mis compañeros. CÓDIGO: ANEXOPE1 VERSIÓN: 1 resultados muestra. arrojados por la INDICADORES DE DESEMPEÑO Reconocer características de los conjuntos de múltiplos y de divisores de un número natural. Resuelve situaciones relacionadas con divisibilidad. Resuelve situaciones relacionadas con números primos y compuestos. Resuelve situaciones relacionadas con el concepto de mínimo común múltiplo. Observa regularidades en la suma de los ángulos interiores de triángulos y cuadriláteros. Reconoce características de diámetros cuerdas, radios y rectas tangentes a una circunferencia. Halla moda y promedio de un conjunto de datos. Analiza y resuelve situaciones relacionadas con moda y promedio. PREGUNTA ÁMBITOS CONTENIDOS PROBLEMATIZADORA CONCEPTUALES Teoría de los Múltiplos y divisores de un número números, Figuras Criterios de divisibilidad; 2, 3, 6, 5 y 10 bidimensionales, Números primos y números compuestos. moda y promedio. Descomposición en factores primos. Mínimo común múltiplo, Máximo común divisor. Triángulos y cuadriláteros. Círculo y circunferencia. Moda. Promedio. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Análisis de imágenes Participación en clase. Trabajos a partir de presentaciones video gráficas. Cuaderno (Toma de nota en clase). Socializaciones de las temáticas. Presentación de Trabajos de manera individual o grupal. Participación en clase. Claridad y coherencia frente a la participación en la solución de elementos geométricos, Ejercicios en clase y casa del texto guía. multiplicaciones y divisiones. Resolución de pruebas escritas Capacidad de argumentar claramente en cada una de las actividades realizadas. Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Ejercicios de profundización sobre geometría y multiplicaciones, divisiones, propiedades y relaciones CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO CUARTO EJES GENERADORES Pensamiento numérico – métrico - aleatorio ESTÁNDARES Interpreto las fracciones en diferentes contextos: situaciones de medición, relaciones parte todo, cociente, razones y proporciones. Reconocer el uso de algunas magnitudes (longitud, área, volumen, capacidad, peso y masa, duración, rapidez, temperatura) y de algunas de las unidades que se usan para medir cantidades de la magnitud respectiva en situaciones aditivas y multiplicativas. Describo la manera como parecen distribuirse los distintos datos de un conjunto de ellos y la comparo con la manera como se distribuyen en otros conjuntos de datos. PREGUNTA PROBLEMATIZADORA TERCERO DISCIPLINAS RELEVANTES COMPETENCIAS INTERPRETACIÓN Y REPRESENTACIÓN Definir las características de un número fraccionario, así como la clase y el procedimiento a utilizar para su ubicación en la recta numérica. Reconoce unidades de superficie del sistema métrico decimal y hacer conversiones entre ellas. Identificar y diferenciar técnicas de conteo. FORMULACIÓN Y EJECUCIÓN Clasificar, ordenar y representar una fracción de diversas maneras, complificar y simplificar un número fraccionario y comparar fracciones heterogéneas. Manejo las propiedades unidades de superficie del sistema métrico decimal y hacer conversiones entre ellas. las Resolver situaciones problema que involucran combinaciones o permutaciones. RAZONAMIENTO Y ARGUMENTACIÓN Inventar o enunciar situaciones en las que se evidencie la aplicabilidad de las operaciones entre números fraccionarios. Creo un ambiente que permita una buena comprensión de las unidades de superficie del sistema métrico decimal y hacer conversiones entre ellas. Argumentar el uso de determinada técnica de conteo para la solución de un problema. INDICADORES DE DESEMPEÑO Establece la relación entre fracciones propias e impropias y la unidad. Resuelve problemas que involucran adición o sustracción de fracciones homogéneas y heterogéneas. Resuelve problemas que involucran multiplicación de fracciones. Establece y resuelve situaciones relacionadas con unidades de superficie. Analiza situaciones reales relacionadas con unidades de volumen. Efectúa conversiones entre unidades de capacidad. Construye arreglos tomando elementos de un conjunto de datos. Determina el número de arreglos que se pueden hacer cumpliendo condiciones dadas. ÁMBITOS CONTENIDOS CONCEPTUALES Números Fracciones, términos y representación fraccionarios, Clases de fracciones. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Fracciones equivalentes. Adición y sustracción de fracciones homogéneas y heterogéneas. Multiplicación de fracciones. Unidades de longitud. Unidades de superficie. Unidades de volumen. Unidades de capacidad. Unidades de masa. Arreglos sin repetición y con repetición. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Análisis de imágenes Participación en clase. Trabajos a partir de presentaciones video gráficas. Cuaderno (Toma de nota en clase). Socializaciones de las temáticas. Presentación de Trabajos de manera individual o grupal. Elaboración de carteleras Claridad y coherencia frente a la participación en la solución de inecuaciones. Ejercicios de consulta. Capacidad de argumentar claramente en cada una de las actividades realizadas. Resolución de pruebas escritas Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Participación activa en clase y constante. Medición, combinación permutación. GRADO y CUARTO EJES GENERADORES Pensamiento numérico – métrico y aleatorio. ESTÁNDARES COMPETENCIAS PERIODO CUARTO DISCIPLINAS RELEVANTES CÓDIGO: ANEXOPE1 VERSIÓN: 1 Describo, comparo y cuantifico situaciones con números, en diferentes contextos y con diversas representaciones. Identifico y justifico relaciones de congruencia y semejanza entre figuras. Conjeturo y pongo a prueba predicciones acerca de la posibilidad de ocurrencia de eventos. PREGUNTA PROBLEMATIZADORA INTERPRETACIÓN Y REPRESENTACIÓN Diferenciar las clases de números decimales y explicar la manera como se realizan las operaciones entre estos. FORMULACIÓN Y EJECUCIÓN Comprender y diferenciar los conceptos de semejanza, congruencia, simetría asimetría, rotación y traslación. Construir figuras en las que se evidencie los criterios de semejanza y congruencia. Efectuar operaciones básicas entre números decimales, entre ellas la división con divisores de 10, 100 o 1000. RAZONAMIENTO Y ARGUMENTACIÓN Analiza la realización de ejercicios o problemas relacionados con los números decimales. Participar en la construcción de figuras en las que se evidencie los conceptos de semejanza, congruencia, simetría. Realizar movimientos de Aceptar la amplia incidencia que Interpretar el concepto de traslación y de rotación de tiene el marco teórico que se refiere probabilidad, resaltando su figuras en el plano. a la probabilidad de ocurrencia de aplicabilidad en algunas eventos, en múltiples decisiones situaciones de la vida cotidiana o Expresar numéricamente la que afectan a una persona o a la actividades económicas probabilidad de un evento. comunidad. específicas. INDICADORES DE DESEMPEÑO Establece la relación entre números decimales y fracciones. Resuelve operaciones con números decimales. Explica la diferencia entre figuras congruentes y figuras semejantes. Aplica traslaciones a figuras geométricas. Identifica características de algunas rotaciones especiales. Determina las condiciones para que un evento sea posible, imposible o seguro. Analiza y resuelve problemas relacionados con el concepto de probabilidad. ÁMBITOS CONTENIDOS CONCEPTUALES Números Decimales, Fracciones, términos y representación transformaciones Clases de fracciones. isométricas, Fracciones equivalentes. probabilidad. Adición y sustracción de fracciones homogéneas y heterogéneas. Multiplicación de fracciones. Figuras congruentes y semejantes. Traslaciones. Rotaciones. Eventos posibles, imposibles y seguros. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Probabilidad de un evento. CRITERIOS DE EVALUACIÓN Participación en clase. Cuaderno (Toma de nota en clase). Presentación de Trabajos de manera individual o grupal. Claridad y coherencia frente a la participación en la solución de inecuaciones. Capacidad de argumentar claramente en cada una de las actividades realizadas. Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Participación activa en clase y constante. ESTRATEGIAS DIDÁCTICAS Análisis de imágenes Trabajos a partir de presentaciones video gráficas. Socializaciones de las temáticas. Elaboración de carteleras Ejercicios de consulta. Resolución de pruebas escritas CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO QUINTO EJES GENERADORES Pensamiento Numérico – Métrico - Aleatorio ESTÁNDARES Resuelvo y formulo problemas cuya estrategia de solución requiera de las relaciones y propiedades de los números naturales y sus operaciones. Utilizo sistemas de coordenadas para especificar localizaciones y describir relaciones espaciales. Comparo y clasifico figuras bidimensionales de acuerdo con sus componentes (ángulos, vértices) y características. Interpreto información presentada en tablas y gráficas. (Pictogramas, gráficas de barras, diagramas de líneas, diagramas circulares). Interpreto información presentada en tablas y gráficas. (Pictogramas, gráficas de barras, diagramas de líneas, diagramas circulares). PERIODO PRIMERO DISCIPLINAS RELEVANTES COMPETENCIAS Interpretación y representación Comprender y Reconoce las diferentes operaciones en el conjunto de los números naturales. Localizar parejas ordenadas en el plano cartesiano. Identificar ángulos según sus medidas y características. Analizar diagramas circulares y gráficos de barras. Formulación y ejecución Resolver problemas relacionados con las operaciones en los números naturales. Representar parejas ordenadas en el plano cartesiano. Clasifica los ángulos según su medida y la suma de sus medidas. Representar parejas ordenadas en el plano cartesiano. Razonamiento y argumentación Inventa actividades que desarrollen los conocimientos relacionados con los números naturales. Justifico regularidades y propiedades de los números, sus relaciones y operaciones. Usa la clasificación de ángulos para establecer el valor de verdad de una afirmación. Inventar encuestas que me lleven a indagar acerca de los gustos de mis compañeros. Recoger datos para la diagramación de gráficos estadísticos. INDICADORES DE DESEMPEÑO Resuelve y formula problemas cuya estrategia de solución requiera de las relaciones y propiedades de los números naturales y sus operaciones. Usa diversas estrategias de cálculo y de estimación para resolver problemas en situaciones aditivas y multiplicativas. Tiene valoración de las operaciones con números naturales como métodos para resolver situaciones de la vida cotidiana. Usa y explica las parejas ordenadas en el plano, polígonos y fórmulas para hallar el área y el perímetro de figuras planas. Compara y clasifica figuras bidimensionales de acuerdo con sus componentes (ángulos y vértices) y características. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Representa datos usando tablas y gráficas. Justifica la información obtenida de diferentes datos. Presenta gusto por el rigor y el orden en la presentación y comunicación de resultados. PREGUNTA ÁMBITOS CONTENIDOS PROBLEMATIZADORA CONCEPTUALES Operaciones con Números naturales. números naturales, Adición y sustracción Plano cartesiano y Propiedades de la adición. Ángulos, Gráficas y Multiplicación y Propiedades de la Multiplicación. datos Estadísticos. Producto Cartesiano y Plano Cartesiano. Ángulos y su clasificación. Construcción de ángulos. Rectas paralelas y perpendiculares. Polígonos Regulares e Irregulares. Variables cualitativas Tabla de Frecuencias. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Socializaciones de las temáticas. Actividades que de evidencia si el estudiante reconoce las diferentes clases de conjuntos. Desarrollar ejercicios de grupo e intercambiar e Coherencia en la justificación y el lenguaje utilizado cuando establece elementos entre intercambiar los diferentes métodos utilizados en la conjuntos. resolución de problemas. Actividades que de evidencia de que representa y resuelve de una forma adecuada situaciones Taller Individual. que involucren unión e intersección de conjuntos. Construir un Domino con los estudiantes utilizando Argumentar claramente en cada situación dada. ejercicios aplicando las diferentes operaciones básicas Determinar si el estudiante es capaz de explicar el conjunto de un complemento y diferencia de y los resultados. un conjunto. Ejercicios de consulta. Participación en los foros y utilizaciones de los medios virtuales. (Blogs, Plataforma, Correo Resolución de pruebas escritas. (Quiz, Exámenes, electrónico). PAL). Presentación de Trabajos de manera individual o grupal. Capacidad de argumentar claramente en cada una de las actividades realizadas. Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades sobre las distintas temáticas. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO QUINTO EJES GENERADORES Pensamiento Numérico y Variacional ESTÁNDARES Resuelvo y formulo problemas cuya estrategia de solución requiera de las relaciones y propiedades de los números naturales y sus operaciones. Identifico la potenciación, la radicación y logaritmación en contextos matemáticos y no matemáticos. Utilizo sistemas de coordenadas para especificar localizaciones y describir relaciones especiales. Reconozco nociones de horizontalidad, verticalidad, paralelismo y perpendicularidad en distintos contextos y su condición relativa con respecto a diferentes sistemas de referencia. Uso e interpreto la media (o promedio) y la mediana y comparo lo que indican. PERIODO SEGUNDO DISCIPLINAS RELEVANTES COMPETENCIAS Interpretación y representación Escribe multiplicaciones de factores iguales usando potenciación. Comprende y reconocer características de los conjuntos de múltiplos y divisores, hallar los múltiplos y los divisores de un número natural. Utiliza, describe sistemas de coordenadas en el plano cartesiano. Identifica las características de las rectas paralelas y perpendiculares. Formulación y ejecución Expresa el significado de la base, el exponente y la potencia. Razonamiento y argumentación Expresar un número natural como el producto de sus factores primos. Explicar la diferencia entre números primos y números compuestos. Reconoce las características del plano cartesiano. Reconocer y construir rectas paralelas y perpendiculares. Usa el significado de la moda, la mediana y el promedio en un conjunto de datos. Argumenta y simplifica problemas utilizando expresiones que contienen potencia, radicales y logaritmos. Explica el producto cartesiano de dos conjuntos. Disfrutar en la representación y trazado de rectas paralelas y perpendiculares. Inventar encuestas que me lleven a indagar acerca de los gustos de mis compañeros. Utilizar las medidas de tendencia central para analizar los resultados arrojados por la muestra. Interpretar el significado de la moda, la mediana y el promedio en un conjunto de datos. INDICADORES DE DESEMPEÑO Interpreta, comprende y justifica las expresiones de potenciación, de radicación y logaritmación. Justifico regularidades y propiedades de los números, sus relaciones y operaciones. Resuelve problemas aplicando la radicación y la potenciación en el conjunto de los números naturales. Reconoce y Halla el mínimo común múltiplo y el máximo común divisor entre dos o más números naturales. Analiza el procedimiento a seguir en la descomposición de números naturales en sus factores primos. Utiliza y analiza sistemas de coordenadas para especificar localizaciones y describir relaciones espaciales. Diseña gráficas utilizando rectas paralelas y perpendiculares. CÓDIGO: ANEXOPE1 VERSIÓN: 1 PREGUNTA PROBLEMATIZADORA Usar e interpretar la moda, media (o promedio) y la mediana y comparar lo que indican. Uso medidas de tendencia central (media, mediana, moda) para interpretar comportamiento de un conjunto de datos. Resuelvo y formulo problemas a partir de un conjunto de datos provenientes de observaciones, consultas o experimentos. ÁMBITOS CONCEPTUALES Operaciones con números naturales, Sistemas de coordenadas, nociones de paralelismo y perpendicularidad. Medidas de Tendencia central. CONTENIDOS Potenciación. Radicación. Logaritmación. Múltiplos y divisores. Números primos y compuestos. Descomposición de números naturales en factores primos y números compuestos. Mínimo común múltiplo, Máximo común divisor. Producto cartesiano. Plano cartesiano. Rectas Paralelas y Perpendiculares. Moda, media y mediana de un conjunto de datos no agrupados. CRITERIOS DE EVALUACIÓN Resuelve situaciones utilizando el concepto de múltiplo y divisor. determinar si el estudiante es capaz de hallar números que cumplan condiciones de divisibilidad y si es capaz de resolver situaciones que involucren criterios de divisibilidad. verificar si los estudiantes son capaces de identificar y hallar el máximo común divisor de un conjunto de números. Cuaderno (Toma de nota en clase). Participación en clase. Sustentar los ejercicios de clase y/o talleres en el tablero. ESTRATEGIAS DIDÁCTICAS Socialización de los contenidos. Actividad del libro Norma para Pensar. Actividad de ampliación plataforma Educa. Juego Interactivo de la Plataforma Educa. Taller en grupos. Juego “Bingo de Múltiplos”. Ejercicios de consulta. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN GRADO QUINTO EJES GENERADORES Pensamiento Numérico – métrico - aleatorio PERIODO TERCERO DISCIPLINAS RELEVANTES CÓDIGO: ANEXOPE1 VERSIÓN: 1 ESTÁNDARES Analizar y explicar las distintas representaciones de un mismo número (naturales, fracciones, decimales, porcentajes). Resuelve ejercicios y problemas de operaciones con números fraccionarios en diferentes contextos matemáticos y cotidianos de forma algorítmica o gráfica. Comparo y clasifico figuras bidimensionales y tridimensionales de acuerdo con sus componentes (ángulos, vértices, caras, lados), características y propiedades. Representa datos usando tablas y gráficas (de barras, diagramas de línea, diagramas circulares). COMPETENCIAS Interpretación y representación Interpreta las fracciones en diferentes contextos: situaciones de medición, razones y proporciones. Planea la solución de problemas con fraccionarios y decimales. Identificar los polígonos regulares de acuerdo al número de ángulos interiores. Interpreta información presentada en tablas y gráficas (de barras, diagramas de líneas, diagramas circulares. Formulación y Razonamiento y argumentación ejecución Representa una fracción Analiza y explica las distintas gráficamente y en la representaciones de un mismo número recta numérica. (naturales, fracciones, decimales, Utiliza la notación porcentajes). decimal para expresar Justifica regularidades y propiedades de los las fracciones en números, sus relaciones y operaciones diferentes contextos. utilizando calculadoras o computadores. Resuelve problemas Participa activamente en la solución de relacionados con los problemas que involucren operaciones con números fraccionarios y números fraccionarios y decimales. los decimales. Analiza el concepto de polígono y su Usar correctamente el clasificación, según diferentes criterios. transportador en la Analiza la información que se presenta por construcción y medición medio de diagrama de barras u otro tipo de polígonas de acuerdo a representación gráfica. sus ángulos interiores. Diseña algún tipo de representación gráfica para organizar los datos presentados en una situación problema. INDICADORES DE DESEMPEÑO Identifica la relación entre fracciones impropias y números mixtos. Compara fracciones homogéneas y heterogéneas y aplica el criterio de equivalencia de fracciones. Domina la adición, la sustracción, la multiplicación y división de fracciones. Inventa y explica problemas aplicando los fraccionarios y decimales. Inventa y explica las parejas ordenadas en el plano, polígonos y fórmulas para hallar el área y el perímetro de figuras planas Clasificar y construir objetos tridimensionales a partir de representaciones bidimensionales y realizar el proceso contrario. Organiza y representa gráficamente datos, en diagramas de barras, circulares. Construir e interpretar gráficas circulares. Resuelve y crea problemas que implican la recolección organización, representación y análisis de datos. CÓDIGO: ANEXOPE1 VERSIÓN: 1 PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES Números fraccionarios y decimales, Figuras bidimensionales y tridimensionales, Proceso Estadístico. ESTRATEGIAS DIDÁCTICAS Socialización de los contenidos. Actividad del libro Norma para Pensar. Actividad de ampliación plataforma Educa. Juego Interactivo de la Plataforma Educa. Taller por medio de imágenes para explicar, representar fracciones en grupos. Construcción de un domino de fracciones. Ejercicios de consulta. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). CONTENIDOS La fracción, sus términos y su representación gráfica. Adición, sustracción, multiplicación y división de fracciones de números mixtos. Fracciones y expresiones decimales. Adición, sustracción, multiplicación y división de números decimales. Polígonos regulares e irregulares. Construcción de polígonos. Prismas y pirámides. Diagramas de doble barra y circulares. Permutaciones y combinaciones. CRITERIOS DE EVALUACIÓN Reconocimiento de la presencia de las fracciones en la vida real como indicadores de parte de un total. Aprecio de la utilidad de trabajar con fracciones que tengan el mismo denominador. Gusto por el rigor y el orden en la presentación y la comunicación de resultados. Utiliza los algoritmos correctos para las operaciones con números fraccionarios. Respuesta coherente con el contexto del problema. Presentar los trabajos en el tiempo estipulado. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO QUINTO EJES GENERADORES Pensamiento Numérico – métrico – aleatorio. ESTÁNDARES Interpretar las fracciones en diferentes contextos: situaciones de medición, razones y proporciones. Diferenciar atributos mensurables de los objetos y eventos (longitud, superficie, volumen, capacidad, masa, tiempo, peso y amplitud angular) en diversas situaciones. Calcular el área, perímetro y volumen de figuras geométricas utilizando dos o más procedimientos equivalentes. Toma decisiones y las justifica a partir de argumentos teóricos o algorítmicos de probabilidad. PERIODO CUARTO DISCIPLINAS RELEVANTES COMPETENCIAS Interpretación y representación Establece razones y proporciones entre diversas cantidades numéricas. Identifica el concepto de magnitudes directa e inversamente proporcionales. Identificar el área lateral, el área, el perímetro total y el volumen de algunos sólidos. Deducir por medio de tablas, listas o diagramas de árbol las posibilidades de que ocurra un evento. Formulación y ejecución Desarrolla razones y proporciones en situaciones problema planteadas en el contexto. Resuelve problemas relacionados con magnitudes directa e inversamente. Efectuar operaciones que permitan conocer el volumen de un sólido. Resolver problemas relacionados con El área y perímetro de figuras planas. Hallar la probabilidad de que ocurra un evento a partir de la determinación del espacio muestral. Razonamiento y argumentación Deduce la aplicabilidad de la proporcionalidad de magnitudes por medio de la regla de tres simple y compuesta, los repartos proporcionales y el cálculo de porcentajes y de interés simple. Argumentar con ejemplos cuales son las medidas de longitud, de masa y de capacidad Argumenta y utiliza la proporcionalidad para resolver problemas de medición. Argumenta la probabilidad de que ocurra un evento. INDICADORES DE DESEMPEÑO Analiza y explica las distintas representaciones de un mismo número (naturales, fracciones, decimales, porcentajes). Resuelve y formula problemas en los cuales se use la proporción directa y la proporción inversa. Modela situaciones de dependencia mediante la proporcionalidad directa e inversa. Diferenciar las unidades cúbicas que se utilizan para medir el volumen de un sólido. Desarrollar el área lateral, área total y volumen de algunos sólidos. Demuestra y explica las fórmulas para hallar el área y el perímetro de figuras geométricas. Resuelvo y formulo problemas a partir de un conjunto de datos provenientes de observaciones, consultas o experimentos. CÓDIGO: ANEXOPE1 VERSIÓN: 1 PREGUNTA PROBLEMATIZADORA Aplica herramientas para predecir la probabilidad de un evento. ÁMBITOS CONCEPTUALES Aplicaciones de la proporcionalidad, Área y volumen del prisma y conversiones de medidas, probabilidad de un evento. ESTRATEGIAS DIDÁCTICAS Socialización de los contenidos. Actividad del libro Norma para Pensar. Actividad de ampliación plataforma Educa. Juego Interactivo de la Plataforma Educa. Taller en grupos. Ejercicios de consulta. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). CONTENIDOS Razones y proporciones. Magnitudes directamente proporcionales. Magnitudes inversamente proporcionales. Regla de tres simple directa. Porcentajes. Facciones, decimales y porcentajes. Sistema internacional de medidas. Unidades de longitud y superficie. Perímetro y área de figuras planas. Unidades de volumen y capacidad. Volumen de prisma Unidad de masa. Permutaciones y combinaciones. Probabilidad de un evento. CRITERIOS DE EVALUACIÓN Colabora con la ejecución de las actividades para la comprensión de problemas que involucran magnitudes directa e inversamente proporcionales. Aplica correctamente la regla de 3 para solucionar problemas Presenta una respuesta coherente con la pregunta de cada problema Conservación de la proporción gráfica en la representación de fracciones. Presentar los trabajos en el tiempo estipulado Presenta una respuesta con un procedimiento lógico. Reconocimiento de los diferentes modelos de fracción utilizando un lenguaje matemático. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN CÓDIGO: ANEXOPE1 VERSIÓN: 1 CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO SEXTO EJES GENERADORES Pensamiento Numérico – métrico – aleatorio. ESTÁNDARES Resuelvo y formulo problemas aplicando propiedades de los números y sus operaciones. PERIODO PRIMERO DISCIPLINAS RELEVANTES COMPETENCIAS Interpretación y representación Identificar y comprender el conjunto de los números naturales. (Valor posicional). Identificar el algoritmo de las operaciones de radicación y potenciación con números naturales. Identificar ángulos según sus medidas y características. Identificar un conjunto de datos de diferentes fuentes de información. Formulación y Razonamiento y argumentación ejecución Resolver problemas Crear situaciones problema a partir de las matemáticos haciendo operaciones entre los números naturales. Comparo y clasifico figuras bidimensionales uso del valor posicional). Argumentar correctamente los pasos a de acuerdo con sus componentes (ángulos, Resolver problemas realizar en los algoritmos de radicación y vértices) y características. aplicando la radicación y potenciación de números naturales. la potenciación en el Usa la clasificación de ángulos para establecer Comparo e interpreto información que conjunto de los números el valor de verdad de una afirmación. obtenga de diferentes fuentes (revistas, naturales. Valorar los datos provistos por los diferentes televisión entrevistas, experimentos y Clasifica los ángulos medios de comunicación, como una fuente otros). según su medida y la que permite tomar decisiones que afectan a suma de sus medidas. los miembros de una comunidad. Interpretar y organizar un conjunto de datos de acuerdo a una información dada. INDICADORES DE DESEMPEÑO Resuelve problemas matemáticos utilizando operaciones y propiedades de los números naturales. Formula situaciones aplicando las propiedades de los números naturales. Resuelve problemas aplicando la radicación y la potenciación en el conjunto de los números naturales. Argumenta correctamente los pasos a realizar en los algoritmos de radicación y potenciación de números naturales. Identifica, mide, construye y clasifica ángulos. Reconoce las clases de un ángulo. Usa diferentes unidades de medida y sus equivalentes. Justifica las diferentes transformaciones que se encuentran en el entorno. Clasifica y ordena diferentes tipos de datos para iniciar su análisis. Justifica la información obtenida de diferentes datos. PREGUNTA ÁMBITOS CONTENIDOS PROBLEMATIZADORA CONCEPTUALES Números naturales y Números Naturales y sistema decimal. sistema de Adición y sustracción de los números naturales. numeración decimal, Ecuaciones de Tipo Aditivo. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Ángulos congruencia segmentos. Gráficas y Estadísticos. y de datos ESTRATEGIAS DIDÁCTICAS Socializaciones de las temáticas. Desarrollar ejercicios de grupo e intercambiar e intercambiar los diferentes métodos utilizados en la resolución de problemas. Taller Individual. Bloques base 10 para el trabajo con números decimales. Multiplicación y división de Números Naturales. Potenciación en los números naturales. Radicación y logaritmación en los números naturales. Elementos de La Geometría. Ángulos y su clasificación. Congruencia de segmentos y ángulos Población. Muestra. Variables estadísticas. Organización de datos. Frecuencia absoluta, relativa y acumulada para datos no agrupados. CRITERIOS DE EVALUACIÓN Cuaderno (Toma de nota en clase). Participación en clase. Sustentar los ejercicios de clase y/o talleres en el tablero. Participación en los foros y utilizaciones de los medios virtuales. (Blogs, Plataforma, Correo electrónico). Presentación de Trabajos de manera individual o grupal. Capacidad de argumentar claramente en cada una de las actividades realizadas. Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades sobre las distintas temáticas. Desarrollar ejercicios para que los estudiantes verifiquen si el valor de la variable satisface o no una ecuación. Ejercicios de consulta. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO SEXTO EJES GENERADORES Pensamiento Numérico – métrico – aleatorio. ESTÁNDARES Encuentro la expresión general (fórmulas) para expresar propiedades de los números naturales, (par, impar, primo) y relaciones entre dos de ellos (múltiplo de divisor de números naturales). Criterios de divisibilidad. Utilizo técnicas y herramientas para la construcción de figuras planas y cuerpos con medidas dadas. Identifico las representaciones gráficas adecuadas para presentar diversos tipos de datos. (Diagramas de barras, diagramas circulares.). PERIODO SEGUNDO DISCIPLINAS RELEVANTES COMPETENCIAS Interpretación y representación Identifica y resuelve los múltiplos y divisores de un número natural. Identificar y construir ángulos y segmentos congruentes. Representa en diagramas de barras, circulares y pictogramas de datos estadísticos. Formulación y ejecución Expresar un número compuesto como producto de factores primos. Usar el concepto de mínimo común múltiplo y máximo común divisor para solucionar problemas en diferentes contextos. Usa el compás para construir rectas paralelas y perpendiculares a una recta dada. Responde preguntas respecto a la información contenida en diagramas de barras y circulares. Recoger datos para la diagramación de gráficos estadísticos. Razonamiento y argumentación Justifica la veracidad de afirmaciones con respecto a los divisores de un número. Justifica procedimientos para encontrar y clasificar números naturales en números primos y números compuestos. Representa y analiza ángulos y segmentos congruentes. Justifica correctamente los símbolos de paralelismo y perpendicularidad. Inventar encuestas que me lleven a indagar acerca de los gustos de mis compañeros. Analizar diagramas circulares y gráficos de barras. INDICADORES DE DESEMPEÑO Identifico resuelvo, formulo y analizo problemas utilizando propiedades básicas de la teoría de números, como la M.C.M el M.C,D, los factores primos y los criterios de divisibilidad. Utilizo técnicas y herramientas para la construcción y reconocimiento de características de elementos geométricos y figuras planas. Establece semejanzas y diferencias entre las transformaciones que pueden efectuarse sobre una figura geométrica. Represento, interpreto y analizo datos usando tablas y gráficos de barras, circulares y pictogramas. CÓDIGO: ANEXOPE1 VERSIÓN: 1 PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES Teoría de números: múltiplos y divisores, factores primos, M.C.M y M.C.D. Construcción de ángulos rectas paralelas y perpendiculares, Gráficas y datos Estadísticos. ESTRATEGIAS DIDÁCTICAS Socializaciones de las temáticas. Actividades del libro Norma para Pensar. Actividades en la plataforma Educa. Construcción de la Criba de Eratóstenes. Película “la Habitación de Fermat” para trabajar el concepto de número primo. Ejercicios de consulta. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). CONTENIDOS Otros sistemas de numeración. Criterios de divisibilidad. Números primos y compuestos. Factorización Prima. Mínimo Común Múltiplo, Máximo Común Divisor. Congruencia de segmentos y ángulos. Rectas paralelas y perpendiculares. Pictogramas. Gráficas de barras y circular. CRITERIOS DE EVALUACIÓN Sustentar su respuesta de acuerdo a la teoría y su análisis. Respuesta coherente con el contexto del problema. Presentar los trabajos en el tiempo estipulado. Representación ordenada de los conjuntos de múltiplos, de divisores, números primos. La correcta utilización de técnicas aplicadas en la teoría de conjuntos como es la descomposición en factores primos. Justificar su uso de operaciones entre conjuntos para resolver problemas y establece vínculos entre el resultado de una operación entre conjuntos y la parte del diagrama de Venn que la representa. Escala de valoración según el SIEE y/o indicaciones de coordinación académica. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN CÓDIGO: ANEXOPE1 VERSIÓN: 1 CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO SEXTO EJES GENERADORES Pensamiento Numérico – métrico – aleatorio. ESTÁNDARES Utilizo números racionales, en sus distintas expresiones (fracciones, razones, decimales o porcentajes) para resolver problemas en contextos de medida. Clasifico polígonos según sus propiedades (número de lados, número de ángulos, longitud de los lados). Predecir y comparar los resultados de aplicar trasformaciones (traslaciones, rotaciones, reflexiones) sobre figuras bidimensionales en situaciones matemáticas. Resolver y formular problemas a partir de un conjunto de datos presentados en tablas, diagramas de barras, diagramas circulares. Predecir y justificar razonamientos y conclusiones usando información estadística. PERIODO TERCERO DISCIPLINAS RELEVANTES COMPETENCIAS Interpretación y representación Identificar los números fraccionarios, sus operaciones y diferentes representaciones. Escribe números mixtos como fracciones impropias y viceversa. Reconocer los polígonos según sus lados, ángulos y longitudes, a partir de figuras geométricas. Identificar y describir las diferentes transformaciones que pueden hacerse con una figura geométrica. Leer, interpretar y representar información en diagramas de barras y circulares. Formulación y Razonamiento y argumentación ejecución Efectuar operaciones Demostrar seguridad en los procedimientos básicas entre números que se reflejen a operaciones entre números fraccionarios. fraccionarios. Determina cuando dos o Explica la validez o no de los procedimientos más fracciones son para realizar adiciones, sustracciones, equivalentes. multiplicaciones y divisiones entre fracciones. Resuelve situaciones Diseñar figuras geométricas con tres, cuatro o relacionadas con la más lados y ángulos. comparación de Mostrar las diferentes transformaciones con fracciones. figuras geométricas tangibles. Clasificar las figuras Aplica razonamientos lógicos en el análisis de geométricas de acuerdo situaciones. al número de lados, ángulos y longitud. Clasificar las diferentes transformaciones que pueden hacerse con una figura geométrica. Representar y leer información estadística en diagramas de línea. INDICADORES DE DESEMPEÑO Identifica los números fraccionarios y sus representaciones en diferentes contextos. Resuelve problemas relacionados con fracciones equivalentes y operaciones entre fraccionarios. Formula problemas utilizando los números fraccionarios. Clasifica y diseña figuras geométricas con diferentes características. Aplica y justifica las diferentes transformaciones que se encuentran en el entorno. Interpretar, producir y comparar representaciones gráficas adecuadas para presentar diversos tipos de datos (diagramas de barras, diagramas circulares). Reconoce la utilidad de los diagramas de líneas en situaciones en las que la información varía en el tiempo. analiza información contenida en gráficos de barras y circulares y saca conclusiones. CÓDIGO: ANEXOPE1 VERSIÓN: 1 PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES Números fraccionarios, Polígonos y transformaciones isométricas, Gráficas y datos Estadísticos. CONTENIDOS Clases de fracciones y números mixtos. Fracciones equivalentes. Adición y sustracción de números fraccionarios. Multiplicación y división de números fraccionarios. Potenciación de números fraccionarios. Radicación y logaritmación de números fraccionarios. Triángulos y su clasificación. Líneas y puntos notables de un triángulo. Polígonos y cuadriláteros. Traslación, Rotación, Reflexión. Diagrama de barras. Diagrama circular. Diagrama de líneas. CRITERIOS DE EVALUACIÓN Conservación de la proporción gráfica en la representación de fracciones. Coherencia entre las representaciones y el contexto del problema. Presentar los trabajos en el tiempo estipulado Presenta una respuesta con un procedimiento lógico Reconocimiento de los diferentes modelos de fracción utilizando un lenguaje matemático. ESTRATEGIAS DIDÁCTICAS Socializaciones de las temáticas. Desarrollar ejercicios de grupo e intercambiar e intercambiar los diferentes métodos utilizados en la resolución de problemas. Taller Individual. Bloques base 10 para el trabajo con números decimales. Desarrollar ejercicios para que los estudiantes verifiquen si el valor de la variable satisface o no una ecuación. Ejercicios de consulta. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN CÓDIGO: ANEXOPE1 VERSIÓN: 1 CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO SEXTO EJES GENERADORES Pensamiento Numérico – métrico - aleatorio ESTÁNDARES Utiliza números en sus diferentes representaciones (fracciones, decimales, razones, porcentaje) para resolver problemas. Identificar relaciones entre distintas unidades utilizadas para medir cantidades de la misma magnitud. Calcular áreas a través de la composición y descomposición de figuras. Usar medidas de tendencia central (media, mediana, moda) para interpretar el comportamiento de un conjunto de datos. PERIODO CUARTO DISCIPLINAS RELEVANTES COMPETENCIAS Interpretación y representación Diferenciar las clases de números decimales, enunciando sus características. Reconoce fracciones decimales y las describe como números decimales. Reconocer las diferentes unidades de longitud. Efectúa mediciones y realiza conversiones. Formulación y Razonamiento y argumentación ejecución Resolver los diferentes Usar el algoritmo para adicionar, sustraer, ejercicios y problemas multiplicar y dividir decimales, y aplicar estas que involucren números operaciones en diferentes contextos. decimales. Interesarse por comprender las diferentes Resolver problemas de maneras como se puede componer o cálculo de áreas descomponer una figura plana. utilizando las diferentes usa las áreas de polígonos, para resolver unidades de medida, y la situaciones problema. composición y Usa el promedio para resolver problemas. descomposición de figuras planas. Resuelve situaciones Reconocer las medidas de que requieren calcular el tendencia central en un perímetro de figuras conjunto de datos, tales como geométricas. media mediana y moda. Utilizar las medidas de tendencia central como información que permite deducir estrategias para la solución de problemas. INDICADORES DE DESEMPEÑO Identifica los números decimales y sus características. Formula y resuelve problemas utilizando los números decimales. Utilizar la notación decimal para expresar las fracciones en diferentes contextos. Reconocer y representar fracciones y decimales de diversas formas. Justificar procedimientos aritméticos utilizando las relaciones y propiedades de las operaciones entre decimales. Define el concepto de área y volumen de una figura plana. Calcula el área, el perímetro y el volumen de diferentes figuras planas. Plantea hipótesis según la información obtenida con las medidas de tendencia central. CÓDIGO: ANEXOPE1 VERSIÓN: 1 PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES Números naturales y sistema de numeración decimal, Medición, Medidas de tendencia central. CONTENIDOS Fracciones decimales Clases de decimales: exactos y periódicos. Decimales equivalentes. Ubicación de decimales en la recta numérica. Comparación de números decimales. Adición y sustracción de números decimales. Multiplicación y división de números decimales. Unidades de longitud. Perímetro. Unidades de área. Área del círculo. Área de polígonos regulares. Moda y mediana para datos no agrupados. Media de datos no agrupados. Organización de información. CRITERIOS DE EVALUACIÓN Respuesta coherente con el contexto del problema. Presentar los trabajos en el tiempo estipulado. Demostrar seguridad en los procedimientos que se reflejen a operaciones entre números decimales. Realiza conversiones entre fracciones decimales y números decimales. Calcula la expresión decimal de una fracción e identifica si es periódico. Usa los números decimales equivalentes en distintas situaciones. No usar la calculadora para realizar operaciones entre números decimales ESTRATEGIAS DIDÁCTICAS Socializaciones de las temáticas. Desarrollar ejercicios de grupo e intercambiar e intercambiar los diferentes métodos utilizados en la resolución de problemas. Taller Individual. Bloques base 10 para el trabajo con números decimales. Desarrollar ejercicios para que los estudiantes verifiquen si el valor de la variable satisface o no una ecuación. Ejercicios de consulta. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN CÓDIGO: ANEXOPE1 VERSIÓN: 1 CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO SÉPTIMO EJES GENERADORES PENSAMIENTO NUMÉRICO, ALEATORIO Y MÉTRICO ESTÁNDARES COMPETENCIAS y Describir situaciones en las cuales se Interpretación presentan los números enteros en sus representación diferentes representaciones. Capacidad de comprender y Emplear las características de los números manipular representaciones de enteros en la solución de situaciones datos cuantitativos o de objetos problemáticas. matemáticos en distintos formatos (textos, tablas, Justificar procesos mediante el manejo de gráficos, diagramas, las diferentes representaciones de los esquemas). Incluye, entre otras números enteros. cosas, la extracción de información local o global (por Utilizar características y relaciones de los ejemplo, la identificación de un números enteros en la solución de promedio, tendencia o patrón); situaciones en diferentes contextos. la comparación de representaciones desde una Aplico las transformaciones rígidas perspectiva comunicativa, la (traslaciones, rotaciones, reflexiones) y representación gráfica y tabular homotecias (ampliaciones y reducciones) de funciones y relaciones. sobre figuras bidimensionales en Pueden requerirse cálculos o estimaciones simples. situaciones matemáticas y en el arte. PRIMERO DISCIPLINAS RELEVANTES Formulación y ejecución Razonamiento y argumentación Consiste en la capacidad de establecer, ejecutar y evaluar estrategias para analizar o resolver problemas que involucren información cuantitativa y objetos matemáticos. Incluye, entre otras cosas, modelar de forma abstracta situaciones reales; analizar los supuestos de un modelo y evaluar su utilidad; escoger y realizar procedimientos (entre los que se incluyen manipulaciones algebraicas y cálculos); evaluar el resultado de un procedimiento. Consiste en la capacidad de justificar juicios sobre situaciones que involucren datos cuantitativos u objetos matemáticos (los juicios pueden referirse a representaciones, modelos, procedimientos, resultados, etc.) a partir de consideraciones o conceptualizaciones matemáticas. Incluye, entre otras cosas, construir o identificar argumentaciones válidas; usar adecuadamente ejemplos y contraejemplos; distinguir hechos de supuestos; reconocer falacias. INDICADORES DE DESEMPEÑO Aplica las operaciones y propiedades de los enteros en la solución de problemas Realiza algunas transformaciones geométricas en el plano cartesiano. Identifica variables y las clasifica de acuerdo con la característica que muestran y con los valores que pueden tomar. Asume una actitud positiva frente a sus deberes como estudiante lasallista. PREGUNTA PROBLEMATIZADORA ¿ Cómo se presentan los números enteros en nuestra ÁMBITOS CONCEPTUALES Números enteros. CONTENIDOS Números enteros, concepto Operaciones con Números enteros Plano cartesiano CÓDIGO: ANEXOPE1 VERSIÓN: 1 vida diaria y cuál es el uso que les damos’ Plano cartesiano y transformaciones en el plano. Estadística. ESTRATEGIAS DIDÁCTICAS Explicación general Actividades Lúdicas Esquemas lógicos, mapas conceptuales Análisis de situaciones Trabajo en grupos Consulta Resolución de pruebas escritas. Reflexión, traslación y rotación Clases de variables Medidas de dispersión CRITERIOS DE EVALUACIÓN Participación en el desarrollo de la clase Revisión de cuaderno Consultas Trabajo individual y grupal Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades. Evaluaciones escritas. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Taller evaluativo, oportunidad en entrega de actividades y evaluación escrita. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO SEPTIMO SEGUNDO EJES GENERADORES DISCIPLINAS RELEVANTES PENSAMIENTO NUMÉRICO, ALEATORIO Y MÉTRICO ESTÁNDARES COMPETENCIAS y Formulación y Razonamiento y argumentación Utiliza números racionales, en sus distintas Interpretación representación ejecución expresiones (fracciones, razones, decimales o porcentajes) para resolver Capacidad de comprender y Consiste en la capacidad de Consiste en la capacidad de manipular representaciones de establecer, ejecutar y evaluar justificar juicios sobre situaciones problemas en contextos de medida. datos cuantitativos o de objetos estrategias para analizar o que involucren datos cuantitativos u matemáticos en distintos resolver problemas que involucren objetos matemáticos (los juicios Reconoce situaciones en las que se usa de formatos (textos, tablas, información cuantitativa y objetos pueden referirse a manera implícita o explícita el concepto de gráficos, diagramas, matemáticos. Incluye, entre otras representaciones, modelos, decimal. esquemas). Incluye, entre otras cosas, modelar de forma abstracta procedimientos, resultados, etc.) a cosas, la extracción de situaciones reales; analizar los partir de consideraciones o Predice y compara los resultados de aplicar información local o global (por supuestos de un modelo y evaluar conceptualizaciones matemáticas. transformaciones (traslaciones, rotaciones, ejemplo, la identificación de un su utilidad; escoger y realizar Incluye, entre otras cosas, construir identificar argumentaciones reflexiones) y homotecias sobre figuras promedio, tendencia o patrón); procedimientos (entre los que se o la comparación de incluyen manipulaciones válidas; usar adecuadamente bidimensionales en situaciones representaciones desde una algebraicas y cálculos); evaluar el ejemplos y contraejemplos; matemáticas y en el arte. perspectiva comunicativa, la resultado de un procedimiento. distinguir hechos de supuestos; reconocer falacias. Interpreto representaciones gráficas representación gráfica y tabular de funciones y relaciones. adecuadas para presentar diversos tipos de Pueden requerirse cálculos o datos. (diagramas de barras, diagramas estimaciones simples. circulares.) INDICADORES DE DESEMPEÑO Identifica el uso de números racionales en diferentes contextos de la vida cotidiana Utiliza tablas de frecuencia, histogramas y polígonos para representar gráficamente un conjunto de datos agrupados. Reconoce y traza los ejes de simetría en polígonos regulares Desarrolla las actividades propuestas y las presenta en el tiempo indicado. PREGUNTA ÁMBITOS CONTENIDOS PROBLEMATIZADORA CONCEPTUALES ¿Cómo surgieron los números Números racionales Concepto de números racionales racionales? Adición y sustracción de números racionales Estadística Tablas de frecuencia para datos agrupados ¿En qué contextos se utilizan Histogramas y polígonos de frecuencia los números racionales? Geometría Ejes de simetría en cuadriláteros y polígonos regulares Homotecia. CÓDIGO: ANEXOPE1 VERSIÓN: 1 ESTRATEGIAS DIDÁCTICAS Explicación general Actividades Lúdicas Esquemas lógicos, mapas conceptuales Análisis de situaciones Trabajo en grupos Consulta Resolución de pruebas escritas CRITERIOS DE EVALUACIÓN Participación en el desarrollo de la clase Revisión de cuaderno Consultas Trabajo individual y grupal Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades. Evaluaciones escritas ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Taller evaluativo, oportunidad en entrega de actividades y evaluación escrita. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO SEPTIMO TERCERO EJES GENERADORES DISCIPLINAS RELEVANTES PENSAMIENTO NUMÉRICO, ALEATORIO Y MÉTRICO ESTÁNDARES COMPETENCIAS y Formulación y Razonamiento y argumentación Utilizo números racionales, en sus distintas Interpretación representación ejecución expresiones (fracciones, razones, decimales o porcentajes) para resolver Capacidad de comprender y Consiste en la capacidad de Consiste en la capacidad de manipular representaciones de establecer, ejecutar y evaluar justificar juicios sobre situaciones problemas en contextos de medida. datos cuantitativos o de objetos estrategias para analizar o que involucren datos cuantitativos u matemáticos en distintos resolver problemas que involucren objetos matemáticos (los juicios Identifico propiedades de las relaciones formatos (textos, tablas, información cuantitativa y objetos pueden referirse a entre números racionales (simétrica, gráficos, diagramas, matemáticos. Incluye, entre otras representaciones, modelos, transitiva, etc.) y de las operaciones entre esquemas). Incluye, entre otras cosas, modelar de forma abstracta procedimientos, resultados, etc.) a ellos (conmutativa, asociativa, etc.) en cosas, la extracción de situaciones reales; analizar los partir de consideraciones o información local o global (por supuestos de un modelo y evaluar conceptualizaciones matemáticas. diferentes contextos. ejemplo, la identificación de un su utilidad; escoger y realizar Incluye, entre otras cosas, construir identificar argumentaciones Interpreto representaciones gráficas promedio, tendencia o patrón); procedimientos (entre los que se o la comparación de incluyen manipulaciones válidas; usar adecuadamente adecuadas para presentar diversos tipos de representaciones desde una algebraicas y cálculos); evaluar el ejemplos y contraejemplos; datos. (diagramas de barras, diagramas perspectiva comunicativa, la resultado de un procedimiento. distinguir hechos de supuestos; circulares.) representación gráfica y tabular reconocer falacias. de funciones y relaciones. Uso medidas de tendencia central (media, Pueden requerirse cálculos o mediana, moda) para interpretar estimaciones simples. comportamiento de un conjunto de datos. INDICADORES DE DESEMPEÑO Emplea ecuaciones para modelar situaciones que involucren estructuras aditivas y multiplicativas Utilizo métodos informales (ensayo y error, Usa medidas de tendencia central para interpretar el comportamiento de un conjunto de datos. complementación) en la solución de Reconoce cuando dos polígonos son congruentes o semejantes Es ordenado y responsable en la entrega de las actividades asignadas. ecuaciones. PREGUNTA PROBLEMATIZADORA ¿En qué situaciones reales se emplean ecuaciones? ÁMBITOS CONCEPTUALES Ecuaciones Estadística Geometría CONTENIDOS Ecuaciones aditivas Ecuaciones multiplicativas Razones y proporciones Proporcionalidad directa, proporcionalidad inversa Moda, mediana y media de datos agrupados CÓDIGO: ANEXOPE1 VERSIÓN: 1 ¿Por qué la variable de una ecuación se representa usualmente con la letra “x”? Congruencia y semejanza de polígonos. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Explicación general Participación en el desarrollo de la clase Actividades Lúdicas Revisión de cuaderno Esquemas lógicos, mapas conceptuales Consultas Análisis de situaciones Trabajo individual y grupal Trabajo en grupos Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en Consulta el desarrollo de las actividades. Resolución de pruebas escritas. Evaluaciones escritas. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Taller evaluativo, oportunidad en entrega de actividades y evaluación escrita. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO SEPTIMO CUARTO EJES GENERADORES DISCIPLINAS RELEVANTES PENSAMIENTO NUMÉRICO, ALEATORIO Y MÉTRICO ESTÁNDARES COMPETENCIAS y Formulación y Razonamiento y argumentación Justifico el uso de representaciones y Interpretación representación ejecución procedimientos en situaciones de Capacidad de comprender y Consiste en la capacidad de Consiste en la capacidad de proporcionalidad directa e inversa. manipular representaciones de establecer, ejecutar y evaluar justificar juicios sobre situaciones Resuelvo y formulo problemas que datos cuantitativos o de objetos estrategias para analizar o que involucren datos cuantitativos u en distintos resolver problemas que involucren objetos matemáticos (los juicios involucren relaciones y propiedades de matemáticos formatos (textos, tablas, información cuantitativa y objetos pueden referirse a semejanza y congruencia usando gráficos, diagramas, matemáticos. Incluye, entre otras representaciones, modelos, representaciones visuales. esquemas). Incluye, entre otras cosas, modelar de forma abstracta procedimientos, resultados, etc.) a cosas, la extracción de situaciones reales; analizar los partir de consideraciones o información local o global (por supuestos de un modelo y evaluar conceptualizaciones matemáticas. ejemplo, la identificación de un su utilidad; escoger y realizar Incluye, entre otras cosas, construir promedio, tendencia o patrón); procedimientos (entre los que se o identificar argumentaciones la comparación de incluyen manipulaciones válidas; usar adecuadamente representaciones desde una algebraicas y cálculos); evaluar el ejemplos y contraejemplos; perspectiva comunicativa, la resultado de un procedimiento. distinguir hechos de supuestos; representación gráfica y tabular reconocer falacias. de funciones y relaciones. Pueden requerirse cálculos o estimaciones simples. INDICADORES DE DESEMPEÑO Justifica los procedimientos usados para solucionar problemas que requieren regla de tres simple y compuesta. Resuelve problemas donde se requiere hallar el área de diferentes polígonos Hace conjeturas acerca del resultado de un experimento aleatorio usando nociones básicas de probabilidad Asume con responsabilidad las diferentes actividades asignadas. PREGUNTA ÁMBITOS CONTENIDOS PROBLEMATIZADORA CONCEPTUALES ¿En qué situaciones de la vida Razones y Regla de tres simple y compuesta real se aplican los conceptos proporciones Porcentaje de proporcionalidad? Prealgebra Estadística Áreas de polígonos CÓDIGO: ANEXOPE1 VERSIÓN: 1 Prismas y cilindros Noción de probabilidad. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Explicación general Participación en el desarrollo de la clase Actividades Lúdicas Revisión de cuaderno Esquemas lógicos, mapas conceptuales Consultas Análisis de situaciones Trabajo individual y grupal Trabajo en grupos Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en Consulta el desarrollo de las actividades. Resolución de pruebas escritas. Evaluaciones escritas. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Taller evaluativo, oportunidad en entrega de actividades y evaluación escrita. Geometría CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO OCTAVO EJES GENERADORES PENSAMIENTO NUMÉRICO, ALEATORIO Y MÉTRICO ESTÁNDARES COMPETENCIAS y Utilizo números reales en sus diferentes Interpretación representaciones y en diversos representación contextos. Capacidad de comprender y manipular representaciones de Resuelvo problemas y simplifico datos cuantitativos o de objetos cálculos usando propiedades y matemáticos en distintos relaciones de los números reales y de formatos (textos, tablas, las relaciones y operaciones entre ellos gráficos, diagramas, esquemas). Incluye, entre otras cosas, la extracción de información local o global (por ejemplo, la identificación de un promedio, tendencia o patrón); la comparación de representaciones desde una perspectiva comunicativa, la representación gráfica y tabular de funciones y relaciones. Pueden requerirse cálculos o estimaciones simples. PREGUNTA PROBLEMATIZADORA ¿De qué forma se puede solucionar problemas de selección y relación de objetos o cosas utilizando los números reales? PRIMERO DISCIPLINAS RELEVANTES Formulación y ejecución Razonamiento y argumentación Consiste en la capacidad de establecer, ejecutar y evaluar estrategias para analizar o resolver problemas que involucren información cuantitativa y objetos matemáticos. Incluye, entre otras cosas, modelar de forma abstracta situaciones reales; analizar los supuestos de un modelo y evaluar su utilidad; escoger y realizar procedimientos (entre los que se incluyen manipulaciones algebraicas y cálculos); evaluar el resultado de un procedimiento. Consiste en la capacidad de justificar juicios sobre situaciones que involucren datos cuantitativos u objetos matemáticos (los juicios pueden referirse a representaciones, modelos, procedimientos, resultados, etc.) a partir de consideraciones o conceptualizaciones matemáticas. Incluye, entre otras cosas, construir o identificar argumentaciones válidas; usar adecuadamente ejemplos y contraejemplos; distinguir hechos de supuestos; reconocer falacias. INDICADORES DE DESEMPEÑO Realiza operaciones con números reales y reconoce las propiedades de las mismas Identifica los conceptos, definiciones, postulados y algunos teoremas básicos de la geometría plana. Elabora tablas de frecuencia, histogramas y polígonos para representar un conjunto de datos agrupados. Asume una actitud positiva frente a sus deberes como estudiante lasallista. ÁMBITOS CONTENIDOS CONCEPTUALES Números reales Números reales: Operaciones y propiedades Razonamiento deductivo, inductivo Estadística Ángulos y rectas perpendiculares Tablas de frecuencia, histogramas y polígonos para datos agrupados. Geometría CÓDIGO: ANEXOPE1 VERSIÓN: 1 ESTRATEGIAS DIDÁCTICAS Explicación general Actividades Lúdicas Esquemas lógicos, mapas conceptuales Análisis de situaciones Trabajo en grupos Consulta Resolución de pruebas escritas CRITERIOS DE EVALUACIÓN Participación en el desarrollo de la clase Revisión de cuaderno Consultas Trabajo individual y grupal Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en el desarrollo de las actividades. Evaluaciones escritas ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Taller evaluativo, teniendo en cuenta que el taller tiene un valor del 60% y la sustentación del 40% CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO OCTAVO SEGUNDO EJES GENERADORES DISCIPLINAS RELEVANTES PENSAMIENTO NUMÉRICO, ALEATORIO Y MÉTRICO ESTÁNDARES COMPETENCIAS y Formulación y ejecución Razonamiento y argumentación Resuelvo problemas y simplifico cálculos Interpretación usando propiedades y relaciones de los representación números reales y de las relaciones y Capacidad de comprender y Consiste en la capacidad de Consiste en la capacidad de justificar operaciones entre ellos. manipular representaciones de establecer, ejecutar y evaluar juicios sobre situaciones que datos cuantitativos o de objetos estrategias para analizar o involucren datos cuantitativos u Construyo expresiones algebraicas matemáticos en distintos resolver problemas que objetos matemáticos (los juicios equivalentes a una expresión algebraica formatos (textos, tablas, involucren información pueden referirse a representaciones, dada. gráficos, diagramas, cuantitativa y objetos modelos, procedimientos, resultados, esquemas). Incluye, entre otras matemáticos. Incluye, entre etc.) a partir de consideraciones o Uso procesos inductivos y lenguaje cosas, la extracción de otras cosas, modelar de forma conceptualizaciones matemáticas. algebraico para formular y poner a prueba información local o global (por abstracta situaciones reales; Incluye, entre otras cosas, construir o conjeturas. ejemplo, la identificación de un analizar los supuestos de un identificar argumentaciones válidas; promedio, tendencia o patrón); modelo y evaluar su utilidad; usar adecuadamente ejemplos y la comparación de escoger y realizar contraejemplos; distinguir hechos de Uso medidas de tendencia central (media, representaciones desde una procedimientos (entre los que se supuestos; reconocer falacias. manipulaciones mediana, moda) para interpretar perspectiva comunicativa, la incluyen representación gráfica y tabular algebraicas y cálculos); evaluar comportamiento de un conjunto de datos. de funciones y relaciones. el resultado de un procedimiento. Interpreto representaciones gráficas Pueden requerirse cálculos o estimaciones simples. adecuadas para presentar diversos tipos de INDICADORES DE DESEMPEÑO datos. (diagramas de barras, diagramas Resuelve situaciones problema a través del uso de operaciones algebraicas circulares.) Describe y representa conjuntos de datos a partir de tablas, diagramas y medidas de tendencia central Identifica las diferentes clases de ángulos y sus características Desarrolla las actividades propuestas y las presenta en el tiempo indicado. PREGUNTA ÁMBITOS CONTENIDOS PROBLEMATIZADORA CONCEPTUALES ¿Cómo se pueden relacionar Polinomios Expresiones algebraicas problemas del quehacer diario Operaciones entre polinomios aplicando las operaciones con Estadística Productos y cocientes notables expresiones algebraicas? Tablas de frecuencia y gráficos para datos ordenados Geometría Medidas de tendencia central para datos agrupados Ángulos y rectas perpendiculares Rectas paralelas y transversales. CÓDIGO: ANEXOPE1 VERSIÓN: 1 CRITERIOS DE EVALUACIÓN ESTRATEGIAS DIDÁCTICAS Explicación general Participación en el desarrollo de la clase Actividades Lúdicas Revisión de cuaderno Esquemas lógicos, mapas conceptuales Consultas Análisis de situaciones Trabajo individual y grupal Trabajo en grupos Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en Consulta el desarrollo de las actividades. Resolución de pruebas escritas. Evaluaciones escritas. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Taller evaluativo, oportunidad en entrega de actividades y evaluación escrita. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO OCTAVO TERCERO EJES GENERADORES DISCIPLINAS RELEVANTES PENSAMIENTO NUMÉRICO, ALEATORIO Y MÉTRICO ESTÁNDARES COMPETENCIAS y Formulación y ejecución Razonamiento y argumentación Uso procesos inductivos y lenguaje Interpretación representación algebraico para formular y poner a prueba Capacidad de comprender y Consiste en la capacidad de Consiste en la capacidad de justificar conjeturas. manipular representaciones de establecer, ejecutar y evaluar juicios sobre situaciones que datos cuantitativos o de objetos estrategias para analizar o involucren datos cuantitativos u Interpreto analítica y críticamente matemáticos en distintos resolver problemas que objetos matemáticos (los juicios información estadística proveniente de formatos (textos, tablas, involucren información pueden referirse a representaciones, diversas fuentes (prensa, revistas, gráficos, diagramas, cuantitativa y objetos modelos, procedimientos, resultados, televisión, experimentos, consultas, esquemas). Incluye, entre otras matemáticos. Incluye, entre etc.) a partir de consideraciones o entrevistas. cosas, la extracción de otras cosas, modelar de forma conceptualizaciones matemáticas. información local o global (por abstracta situaciones reales; Incluye, entre otras cosas, construir o Interpreto y utilizo conceptos de media, ejemplo, la identificación de un analizar los supuestos de un identificar argumentaciones válidas; mediana y moda y explicito sus diferencias promedio, tendencia o patrón); modelo y evaluar su utilidad; usar adecuadamente ejemplos y comparación de escoger y realizar contraejemplos; distinguir hechos de en distribuciones de distinta dispersión y la representaciones desde una procedimientos (entre los que se supuestos; reconocer falacias. asimetría. perspectiva comunicativa, la incluyen manipulaciones representación gráfica y tabular algebraicas y cálculos); evaluar de funciones y relaciones. el resultado de un procedimiento. Pueden requerirse cálculos o estimaciones simples. INDICADORES DE DESEMPEÑO Identifica diferentes métodos para factorizar expresiones algebraicas Identifica el concepto de probabilidad y su aplicación Reconoce diferentes postulados que sirven como criterio para establecer congruencia de un par de triángulos Es ordenado y responsable en la entrega de las actividades asignadas. PREGUNTA ÁMBITOS CONTENIDOS PROBLEMATIZADORA CONCEPTUALES ¿Cómo conceptualizar y Factorización Factor común y factor común por agrupación construir espacios sociales a Factorización de trinomios través del manejo del algebra Estadística Diferencia de cuadrados geométrica y sus aplicaciones Diferencia y suma de cubos aritméticas? Geometría Factorizaciones combinadas CÓDIGO: ANEXOPE1 VERSIÓN: 1 Ángulos internos y externos de un triángulo Congruencia de triángulos Espacio muestral, eventos simples y compuestos Concepto de probabilidad. CRITERIOS DE EVALUACIÓN ESTRATEGIAS DIDÁCTICAS Explicación general Participación en el desarrollo de la clase Actividades Lúdicas Revisión de cuaderno Esquemas lógicos, mapas conceptuales Consultas Análisis de situaciones Trabajo individual y grupal Trabajo en grupos Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en Consulta el desarrollo de las actividades. Resolución de pruebas escritas Evaluaciones escritas. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Taller evaluativo, oportunidad en entrega de actividades y evaluación escrita. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO OCTAVO CUARTO EJES GENERADORES DISCIPLINAS RELEVANTES PENSAMIENTO NUMÉRICO, ALEATORIO Y MÉTRICO ESTÁNDARES COMPETENCIAS y Formulación y ejecución Razonamiento y argumentación Reconozco y contrasto propiedades y Interpretación representación relaciones geométricas utilizadas en demostraciones de teoremas básicos Capacidad de comprender y Consiste en la capacidad de Consiste en la capacidad de justificar manipular representaciones de establecer, ejecutar y evaluar juicios sobre situaciones que (Pitágoras y Tales.) datos cuantitativos o de objetos estrategias para analizar o involucren datos cuantitativos u matemáticos en distintos resolver problemas que objetos matemáticos (los juicios Construyo expresiones algebraicas formatos (textos, tablas, involucren información pueden referirse a representaciones, equivalentes a una expresión algebraica gráficos, diagramas, cuantitativa y objetos modelos, procedimientos, resultados, dada. esquemas). Incluye, entre otras matemáticos. Incluye, entre etc.) a partir de consideraciones o cosas, la extracción de otras cosas, modelar de forma conceptualizaciones matemáticas. Interpreto analítica y críticamente información local o global (por abstracta situaciones reales; Incluye, entre otras cosas, construir o información estadística proveniente de ejemplo, la identificación de un analizar los supuestos de un identificar argumentaciones válidas; diversas fuentes (prensa, revistas, promedio, tendencia o patrón); modelo y evaluar su utilidad; usar adecuadamente ejemplos y comparación de escoger y realizar contraejemplos; distinguir hechos de televisión, experimentos, consultas, la representaciones desde una procedimientos (entre los que se supuestos; reconocer falacias. entrevistas. perspectiva comunicativa, la incluyen manipulaciones representación gráfica y tabular algebraicas y cálculos); evaluar de funciones y relaciones. el resultado de un procedimiento. Pueden requerirse cálculos o estimaciones simples. INDICADORES DE DESEMPEÑO Identifica diferentes métodos para simplificar expresiones algebraicas Identifica las características y propiedades de los paralelogramos Analiza y amplía la información contenida en un grupo de datos a partir de la distribución de frecuencias y gráficas dadas. Asume con responsabilidad las diferentes actividades asignadas. PREGUNTA ÁMBITOS CONTENIDOS PROBLEMATIZADORA CONCEPTUALES ¿Qué situaciones de la vida Fracciones algebraicas Operaciones con fracciones algebraicas diaria se pueden modelar para Ecuaciones con fracciones algebraicas construir y resolver Funciones Concepto de función ecuaciones lineales de primer Paralelogramos grado? Estadística Análisis de distribución de frecuencia y gráficos. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Geometría ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Explicación general Participación en el desarrollo de la clase Actividades Lúdicas Revisión de cuaderno Esquemas lógicos, mapas conceptuales Consultas Análisis de situaciones Trabajo individual y grupal Trabajo en grupos Puntualidad en la entrega de trabajos, manejo del tiempo dentro y fuera del salón de clase en Consulta el desarrollo de las actividades. Resolución de pruebas escritas Evaluaciones escritas. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Taller evaluativo, oportunidad en entrega de actividades y evaluación escrita. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO Noveno EJES GENERADORES Pensamientos numérico, Variacional, Espacial y Aleatorio ESTÁNDARES COMPETENCIAS y Identifico y utilizo la potenciación, la Interpretación radicación y la logaritmación para representación representar situaciones matemáticas y no Identificar el conjunto de los números reales. matemáticas y para resolver problemas. Uso representaciones geométricas para resolver y formular problemas en las matemáticas y en otras disciplinas. Resuelvo y formulo problemas seleccionando información relevante en conjuntos de datos provenientes de fuentes diversas. PREGUNTA PROBLEMATIZADORA ¿Cuáles son los usos que se pueden hacer de los números pertenecientes a los diferentes conjuntos numéricos en el ámbito de los reales? Resuelve e interpreta situaciones que involucran inecuaciones con valor absoluto Primero DISCIPLINAS RELEVANTES Formulación y ejecución Resuelvo problemas y simplifico cálculos usando propiedades y relaciones de los números reales y de las relaciones y operaciones entre ellos. Razonamiento y argumentación Argumenta sus ideas para verificar o refutar afirmaciones relacionadas con el complemento y diferencia de un conjunto. Representa gráficamente un número complejo y su conjugado INDICADORES DE DESEMPEÑO Identificar el conjunto de los números reales. Resuelve ecuaciones con valor absoluto Racionaliza expresiones racionales. Clasifica números en los diferentes conjuntos numéricos. Representa gráficamente un número complejo y su conjugado. Soluciona situaciones con adición, sustracción, multiplicación y división de números complejos Utiliza el concepto de pendiente para dar solución a situaciones problemáticas Representa gráficamente las soluciones de una ecuación lineal con dos variables. Utiliza el método de sustitución para hallar la solución de un problema. Encuentra la solución de un sistema 2x2 mediante el método de igualación. ÁMBITOS CONCEPTUALES Sistemas numéricos reales y complejos. CONTENIDOS Números reales. Ecuaciones con valor absoluto. Inecuaciones con valor absoluto. Exponentes y sus propiedades. teorema de Pitágoras semejanza en triángulos rectángulo. Racionalización. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Sistema de los números complejos. Modulo y conjugado de un numero complejo. Adición, sustracción, multiplicación y división de números complejos La recta y su pendiente. Ecuación general de la recta Ecuaciones lineales con dos variables. Solución grafica de un sistema de ecuaciones lineales. Método de sustitución. Método de igualación. Método de eliminación. Método de reducción Determinante y regla de cramer.. Solución de problemas con ecuaciones. De una incógnita. Sistema de tres ecuaciones y tres incógnitas Inecuaciones lineales ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Socializaciones de las temáticas. Actividades que de evidencia si el estudiante reconoce los números reales Desarrollar ejercicios de grupo e intercambiar e Coherencia en la justificación y el lenguaje utilizado cuando establece elementos entre intercambiar los diferentes métodos utilizados en la conjuntos. resolución de problemas. Actividades que de evidencia de que representa y resuelve de una forma adecuada situaciones Taller Individual. que involucren números complejos y su conjugado Construir un Domino con los estudiantes utilizando Argumentar claramente en cada situación dada. ejercicios aplicando las diferentes operaciones básicas y los resultados. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN GRADO PERIODO Noveno SEGUNDO EJES GENERADORES Pensamiento Espacial y Sistemas Geométricos, Pensamiento métrico y sistema de medidas ESTÁNDARES COMPETENCIAS Interpretación y Formulación representación ejecución DISCIPLINAS RELEVANTES y Razonamiento y argumentación CÓDIGO: ANEXOPE1 VERSIÓN: 1 Identificar la pendiente de una recta. Utiliza el concepto de pendiente para dar solución a situaciones problemas. Identificar la ecuación general de una recta. Identificar ecuaciones lineales con dos variables. Determinar cuándo equivalentes. dos sistemas son Localizar parejas ordenadas en el plano cartesiano, para formar una línea recta. Parejas ordenadas en el plano cartesiano en la graficacion de una recta Respetar las opiniones de los compañeros a la hora de esclarecer conceptos relacionados con la geometría. Identifica en una recta el Clasifica la rectas según Usa la clasificación de las funciones para hallar acenso o descenso, para su punto de origen.. el conjunto solución a una situación problemica clasificarla en creciente o de cotidiana. creciente. INDICADORES DE DESEMPEÑO Adiciona y sustrae números complejos Enuncia y halla el opuesto de un número complejo. Determina el inverso multiplicativo de un número complejo. Jerarquiza multiplicación y división de números complejos Describe la pendiente de una recta Localiza la pendiente de una recta Maneja el concepto de pendiente para dar solución a situaciones Describe la ecuación general de una recta . Explica si un punto pertenece a una recta conociendo su ecuación Identifica las condiciones para que dos rectas sean paralelas o perpendiculares. Diseña soluciones a problemas que requieren el manejo de rectas paralelas o perpendiculares Identifica la solución de sistemas de ecuaciones lineales 2x2 Concibe decisiones basados en la solución de un sistema de ecuaciones lineales 2x2 Concreta la solución de un sistema 2x2 mediante el método de sustitución. Utiliza el método de sustitución para hallar la solución de un problema Identifica si un punto pertenece al conjunto solución de una inecuación lineal con dos variables. Establece el conjunto solución de una inecuación lineal con dos variables. Utiliza la región del plano que da solución a un conjunto de inecuaciones lineales. Plantea y resuelve problemas que requieren el manejo de sistemas de inecuaciones lineales. Identifica ecuaciones cuadráticas Determina si un valor es solución de una ecuación cuadrática Comprende la propiedad del factor nulo. Modifica la solución de ecuaciones cuadráticas por factorización Comprende la propiedad de la raíz cuadrada. CÓDIGO: ANEXOPE1 VERSIÓN: 1 PREGUNTA PROBLEMATIZADORA ¿Cuál es la importancia de los pensamientos espaciales y numéricos en el desarrollo tecnológico de este mundo moderno? ÁMBITOS CONCEPTUALES Funciones trigonométricas II y las razones trigonométricas. CONTENIDOS La recta y su pendiente. Ecuación general de la recta. Rectas paralelas y perpendiculares. Ecuaciones lineales con dos variables. Solución grafica de un sistema de ecuaciones lineales Método de sustitución Método de igualación Método de eliminación Determinantes y regla de cramer. Sistema de tres ecuaciones y tres incógnitas. Inecuaciones lineales Sistemas de inecuaciones Ecuación cuadrática Solución de ecuaciones cuadráticas por factorización Método de completar el cuadrado. Formula cuadrática Aplicación de la ecuación cuadrática. Inecuaciones cuadráticas. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Socializaciones de las temáticas. Cuaderno (Toma de nota en clase). Desarrollar ejercicios de grupo e intercambiar e Participación en clase. intercambiar los diferentes métodos utilizados en la Sustentar los ejercicios de clase y/o talleres en el tablero. resolución de problemas con la utilización de razones Participación en los foros y utilizaciones de los medios virtuales. (Blogs, Plataforma, Correo trigonométricas. electrónico). Desarrollar ejercicios en los que sea necesario utilizar Presentación de Trabajos de manera individual o grupal. el transportador y compas para su solución y graficacion de figuras con razones trigonométricas. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Continua durante los periodos. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO Noveno Tercero EJES GENERADORES DISCIPLINAS RELEVANTES Pensamientos numérico, Variacional, Espacial y Aleatorio ESTÁNDARES COMPETENCIAS y Formulación y Razonamiento y argumentación Interpreta y aplica la definición de dominio y Interpretación representación ejecución rango de una función. Interpreto y represento Propongo y resuelvo Analiza y manifiesta de forma verbal y escrita modelos matemáticos para situaciones problemas situaciones que contienen el uso de técnicas Halla la solución de ecuaciones cuadráticas resolver ejercicios de que involucran de conteo con repetición y sin repetición. por factorización. ecuaciones 2x2 por los volúmenes de sólidos. métodos de sustitución, Determina el valor de una matriz 2x2. eliminación y determinantes. Resuelve un sistema de tres ecuaciones INDICADORES DE DESEMPEÑO Encuentra la solución de un sistema de ecuaciones 2x2 mediante los métodos de sustitución, con 3 incógnitas. eliminación o determinantes. Resuelve problemas a partir del lenguaje algebraico y simbólico de las ecuaciones lineales 2x2 a partir de los métodos de sustitución, eliminación y determinantes. Resuelve problemas de volumen de sólidos. Toma decisiones y las justifica a partir de argumentos teóricos o algorítmicos de técnicas de conteo con repetición. Resuelve problemas de ecuaciones lineales 2x2 a partir del leguaje simbólico y algebraico. Halla el volumen de un cilindro y de un cono en ejercicios y situaciones problemas. Identifica resultados ordenados y sin repetición. Aplica adecuadamente las expresiones para determinar la cantidad total de resultados. Identifica y representa la ecuación general de la recta para establecer si un punto pertenece a una recta conociendo su ecuación. Halla la solución de ecuaciones cuadráticas a partir del reconocimiento de características de dichas soluciones por medio de factorización y la formula general. Aplica teoremas sobre rectas tangentes, cuerdas, arcos, ángulos centrales y ángulos inscritos en la circunferencia. Justifica afirmaciones relacionadas con propiedades de las funciones lineales. Interpreta y aplica la definición de función lineal y sus casos particulares en la clasificación de diversas funciones. PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES CONTENIDOS CÓDIGO: ANEXOPE1 VERSIÓN: 1 ¿CÚAL ES LA IMPORTANCIA DE LA MATEMATICA EN LA VIDA COTIDIANA?. Pensamiento numérico variacional Pensamiento métrico y geométrico. Pensamiento aleatorio. . Métodos de eliminación y determinante de ecuaciones 2x2 Volumen de un prisma y una pirámide. Técnicas de conteo con repetición. Problemas de aplicación con ecuaciones 2x2 a partir del leguaje algebraico y simbólico de las ecuaciones. Volúmenes de cuerpos redondos. Técnicas de conteo sin repetición. Pendiente de una recta y ecuación general de la recta. Ecuaciones cuadráticas y sus aplicaciones. Circunferencia. Función lineal y función cuadrática. Probabilidad de eventos compuestos y ley de adición. Métodos de eliminación y determinante de ecuaciones 2x2. Volumen de un prisma y una pirámide. Técnicas de conteo con repetición. Problemas de aplicación con ecuaciones 2x2 a partir del leguaje algebraico y simbólico de las ecuaciones. Volúmenes de cuerpos redondos. Técnicas de conteo sin repetición. Pendiente de una recta y ecuación general de la recta. Ecuaciones cuadráticas y sus aplicaciones. Circunferencia. CRITERIOS DE EVALUACIÓN Actividades que de evidencia si el estudiante reconoce los números reales. Coherencia en la justificación y el lenguaje utilizado cuando establece elementos entre conjuntos. Actividades que de evidencia de que representa y resuelve de una forma adecuada situaciones que involucren números complejos y su conjugado. Argumentar claramente en cada situación dada. ESTRATEGIAS DIDÁCTICAS Socializaciones de las temáticas. Desarrollar ejercicios de grupo e intercambiar e intercambiar los diferentes métodos utilizados en la resolución de problemas. Taller Individual. Construir un Domino con los estudiantes utilizando ejercicios aplicando las diferentes operaciones básicas y los resultados. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN GRADO Noveno EJES GENERADORES PERIODO cuarto DISCIPLINAS RELEVANTES CÓDIGO: ANEXOPE1 VERSIÓN: 1 Pensamiento Espacial y Sistemas Geométricos, Pensamiento métrico y sistema de medidas ESTÁNDARES COMPETENCIAS Interpretación y Formulación y Razonamiento y argumentación representación ejecución Resuelvo problemas utilizando las Localizar parejas ordenadas en Representar parejas Respetar las opiniones de los compañeros a operaciones sobre funciones. el plano cartesiano, para ordenadas en el plano la hora de esclarecer conceptos relacionados formar una línea recta. cartesiano en la con la geometría. Resuelvo problemas que involucran graficacion de una recta Usa la clasificación de las funciones para hallar sucesiones y series. Identifica en una recta el Clasifica la rectas según el conjunto solución a una situación problemica acenso o descenso, para cotidiana. su punto de origen.. Aplica teoremas sobre rectas tangentes a clasificarla en creciente o de una circunferencia en la resolución de creciente. problemas. INDICADORES DE DESEMPEÑO Reconoce ángulos inscritos en una Determina el conjunto solución de funciones. circunferencia y establece la relación entre Identifica caras, vértices y aristas en un poliedro. su medida y la medida del arco intersecado. Justifica afirmaciones relacionadas con las propiedades de las funciones lineales. Reconoce ángulos inscritos en una circunferencia y establece la relación entre sus medidas y la medida del arco intersecado. Usa las funciones logarítmicas en diferentes contextos. identifica los tipos de polígonos que forman las caras laterales y las bases de prisma y pirámides. Determina el conjunto solución de una sucesión aritmética. Justifica afirmaciones que involucran definiciones relacionadas con sucesiones Reconoce situaciones de la vida cotidiana en las que intervienen sucesiones geométricas. Ejemplifica series aritméticas. PREGUNTA PROBLEMATIZADORA ¿Cuál es el aporte de las funciones, desde la teoría y la práctica para el desarrollo de las ciudades en el campo de la construcción?. ÁMBITOS CONCEPTUALES Pensamiento variacional y métrico. CONTENIDOS Función cuadrática Función exponencial Sólidos geométricos. Función lineal y afín. Ángulos inscritos Función logarítmica Área de prisma y pirámide. CÓDIGO: ANEXOPE1 VERSIÓN: 1 ESTRATEGIAS DIDÁCTICAS Socializaciones de las temáticas. Desarrollar ejercicios de grupo e intercambiar e intercambiar los diferentes métodos utilizados en la resolución de problemas con la utilización de razones trigonométricas. Desarrollar ejercicios en los que sea necesario utilizar el transportador y compas para su solución y graficacion de figuras con razones trigonométricas. Sucesiones: creciente y decreciente Sucesión aritmética Sucesión geométrica Series Series aritméticas Triángulos rectángulos especiales Cuerda, arcos y ángulos centrales. .Elementos de la circunferencia Razones trigonométricas. CRITERIOS DE EVALUACIÓN Cuaderno (Toma de nota en clase). Participación en clase. Sustentar los ejercicios de clase y/o talleres en el tablero. Participación en los foros y utilizaciones de los medios virtuales. (Blogs, Plataforma, Correo electrónico). Presentación de Trabajos de manera individual o grupal. Elaboración de estructuras apartir de las diferentes tematicas ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Continúa durante los periodos. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO Decimo EJES GENERADORES Pensamientos numérico, Variacional, Espacial y Aleatorio ESTÁNDARES COMPETENCIAS y Describo y modelo fenómenos periódicos Interpretación del mundo real usando relaciones y representación Comprender y Reconoce las funciones trigonométricas. diferentes operaciones para Diseño estrategias para abordar situaciones calcular el valor de un ángulo de medición que requieran grados de en diferentes sistemas y contextos. precisión específicos. PREGUNTA PROBLEMATIZADORA ¿Cómo con cuáles herramientas básicas de la trigonometría, puedo medir distancias y ángulos de mi entorno? ¿Cómo diseñarías un instrumento que permita medir los diversos ángulos de tu entorno? Primero DISCIPLINAS RELEVANTES Formulación y ejecución Resuelve permutación en situaciones cotidiana. Resolver problemas relacionados con las operaciones entre conjuntos de datos. Razonamiento y argumentación Argumenta sus ideas para verificar o refutar afirmaciones relacionadas con el complemento y diferencia de un conjunto. Halla el valor de una permutación en situaciones cotidiana. Determina las características de un tipo de población, a partir de una muestra. INDICADORES DE DESEMPEÑO Comprende y calcula el valor de un ángulo en diferentes sistemas y contextos Determina la mediada de un ángulo en cualquier contexto Establece relaciones entre las longitudes de los lados de un triángulo rectángulo Diferencia la estadística descriptiva de la inferencial. Determina las características de un tipo de población, a partir de una muestra. Identifica variables estadísticas en cualquier situación. Halla el valor de una permutación en situaciones cotidiana. Combina datos y halla su máxima expresión en una situación problema. ÁMBITOS CONTENIDOS CONCEPTUALES OPERACIONES CON Ángulos Descripción e inferencia. RAZONES Ángulos sobre el plano cartesiano. TRIGONOMETRICA Medición de ángulos S. Longitud de arco. Triángulos rectángulos. Distancia entre dos puntos. Área, perímetro y comprobación de igualdad del triángulo. Descripción e inferencia. Población y muestra. Variables estadísticas. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Datos agrupados Datos no agrupados. Experimentos aleatorios y espacios muéstrales Eventos. Permutaciones. Combinatorias. Probabilidad. ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Socializaciones de las temáticas. Actividades que de evidencia si el estudiante reconoce las razones trigonométricas Desarrollar ejercicios de grupo e intercambiar e Coherencia en la justificación y el lenguaje utilizado cuando establece elementos entre intercambiar los diferentes métodos utilizados en la conjuntos. resolución de problemas. Actividades que de evidencia de que representa y resuelve de una forma adecuada situaciones Taller Individual. que involucren razones trigonométricas Construir un Domino con los estudiantes utilizando Argumentar claramente en cada situación dada. ejercicios aplicando las diferentes operaciones básicas Determinar si el estudiante es capaz de explicar razones trigonométricas y los resultados. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN GRADO PERIODO DECIMO SEGUNDO EJES GENERADORES DISCIPLINAS RELEVANTES Pensamiento Espacial y Sistemas Geométricos, Pensamiento métrico y sistema de medidas ESTÁNDARES COMPETENCIAS y Formulación y Razonamiento y argumentación Comprende y calcula el valor de un ángulo Interpretación representación ejecución en diferentes sistemas y Contextos Localizar parejas ordenadas en Representar parejas Respetar las opiniones de los compañeros a Establece relaciones y características entre el plano cartesiano. ordenadas en el plano la hora de esclarecer conceptos relacionados las razones trigonométricas de los ángulos cartesiano en la con la geometría. Identificar ángulos según sus de 30°, 45° y 60°. graficacion de ángulos. medidas y características. Usa la clasificación de las funciones para hallar Describe y determina el origen de igualdad de una identidad trigonométrica. Clasifica los ángulos según su medida y la suma de sus medidas. el conjunto solución a una situación problemica cotidiana. CÓDIGO: ANEXOPE1 VERSIÓN: 1 Representa contextos. funciones en PREGUNTA PROBLEMATIZADORA ¿Cuál es la importancia de los pensamientos espaciales y numéricos en el desarrollo tecnológico de este mundo moderno? INDICADORES DE DESEMPEÑO Identifica las características de una función a partir de su expresión analítica Reconoce las identidades que puede aplicar en la solución de una ecuación Hace uso de ecuaciones cuadráticas para modelar situaciones de manera matemática. Analiza en representaciones gráficas cartesianas las características de una función y su inversa. Hace uso de ecuaciones cuadráticas para representar situaciones de manera matemática. Analiza en representaciones gráficas cartesianas las características de una función y su inversa Aplica los conocimientos que tiene de ángulos notables para solucionar ecuaciones básicas. Reconoce las identidades que puede aplicar en la solución de una ecuación Relaciona información gráfica con datos analítico Usa la circunferencia unitaria como base para construir las funciones trigonométricas Soluciona problemas que involucren para su solución, las funciones trigonométricas y su inversa Encuentra valores para los cuales una ecuación no tiene solución ÁMBITOS CONTENIDOS CONCEPTUALES Funciones Función trigonométricas II y Dominio de una función las razones Rango de una función trigonométricas. Funciones inyectivas, sobreyectivas y biyectiva Función lineal Función afín Función cuadrática Función cubica Función exponencial Función logarítmica Triangulo rectángulo Razones trigonométricas de triángulos rectángulos Razones de ángulos especiales Identidades trigonométricas fundamentales Aplicaciones de las funciones trigonométricas Funciones circulares. Definición de las funciones trigonométricas de ángulos en posición normal. Razones trigonométricas para 30°, 45° y 60° Funciones trigonométricas para ángulos coterminales todos los CÓDIGO: ANEXOPE1 VERSIÓN: 1 ESTRATEGIAS DIDÁCTICAS Socializaciones de las temáticas. Desarrollar ejercicios de grupo e intercambiar e intercambiar los diferentes métodos utilizados en la resolución de problemas con la utilización de razones trigonométricas. Ángulos de elevación y depresión. CRITERIOS DE EVALUACIÓN Cuaderno (Toma de nota en clase). Participación en clase. Sustentar los ejercicios de clase y/o talleres en el tablero. Participación en los foros y utilizaciones de los medios virtuales. (Blogs, Plataforma, Correo electrónico). Presentación de Trabajos de manera individual o grupal. Desarrollar ejercicios en los que sea necesario utilizar el transportador y compas para su solución y graficacion de figuras con razones trigonométricas. ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Continua durante los periodos. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO Decimo EJES GENERADORES Pensamientos numérico, Variacional, Espacial y Aleatorio ESTÁNDARES COMPETENCIAS y Analiza información que puedo obtener de Interpretación las gráficas de las funciones trigonométricas representación para trazar la gráfica de transformación de Comprender y Reconoce las diferentes operaciones para estas. calcular el valor de un ángulo en diferentes sistemas y Determina el ángulo de referencia para un contextos. ángulo medido en radianes o grados. DISCIPLINAS RELEVANTES Formulación y ejecución Resuelve permutación en situaciones cotidiana. Resolver problemas relacionados con las operaciones entre conjuntos de datos Razonamiento y argumentación Argumenta sus ideas para verificar o refutar afirmaciones relacionadas con el complemento y diferencia de un conjunto. Halla el valor de una permutación en situaciones cotidiana. Determina las características de un tipo de población, a partir de una muestra. INDICADORES DE DESEMPEÑO Comprende y calcula el valor de un ángulo en diferentes sistemas y contextos Determina la mediada de un ángulo en cualquier contexto Establece relaciones entre funciones seno, coseno y tangente, con sus inversas. Diferencia la estadística descriptiva de la inferencial. Determina las características de un tipo de población, a partir de una muestra. Identifica variables estadísticas en cualquier situación. Halla el valor de una permutación en situaciones cotidiana. Combina datos y halla su máxima expresión en una situación problema. ÁMBITOS CONCEPTUALES CONTENIDOS Justifica matemáticamente respuestas con base en las funciones trigonométricas. PREGUNTA PROBLEMATIZADORA ¿Cuál es la importancia de las matemáticas en la vida del estudiante de la media vocacional y profesional?. Tercero Pensamiento variacional numérico y Inversa de la función seno Inversa de la función coseno Inversa de la tangente y la cotangente Inversa de las funciones secante y cosecante Aplicaciones de las funciones trigonométricas inversas. Teorema o ley del seno Teorema o ley del coseno Identidades trigonométricas Identidades para la suma y la diferencia de ángulos Identidades para productos Operaciones algebraicas con funciones trigonométricas(suma y resta) CÓDIGO: ANEXOPE1 VERSIÓN: 1 ESTRATEGIAS DIDÁCTICAS Socializaciones de las temáticas. Desarrollar ejercicios de grupo e intercambiar e intercambiar los diferentes métodos utilizados en la resolución de problemas. Taller Individual. Construir un Domino con los estudiantes utilizando ejercicios aplicando las diferentes operaciones básicas y los resultados. Resolución de pruebas escritas. (Quiz, Exámenes, PAL). Multiplicación de expresiones trigonométricas División de expresiones trigonométricas Factorización de expresiones con funciones trigonométricas Sistema de ecuaciones trigonométricas. CRITERIOS DE EVALUACIÓN Actividades que de evidencia si el estudiante reconoce las razones trigonométricas. Coherencia en la justificación y el lenguaje utilizado cuando establece elementos entre conjuntos. Actividades que de evidencia de que representa y resuelve de una forma adecuada situaciones que involucren razones trigonométricas. Argumentar claramente en cada situación dada. Determinar si el estudiante es capaz de explicar razones trigonométricas ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN GRADO PERIODO DECIMO Cuarto. EJES GENERADORES DISCIPLINAS RELEVANTES Pensamiento Espacial y Sistemas Geométricos, Pensamiento métrico y sistema de medidas ESTÁNDARES COMPETENCIAS y Formulación y Razonamiento y argumentación Analiza información que puedo obtener de Interpretación ejecución las gráficas de las funciones trigonométricas representación parejas Respetar las opiniones de los compañeros a para trazar la gráfica de transformación de Localizar parejas ordenadas en Representar el plano cartesiano. ordenadas en el plano la hora de esclarecer conceptos relacionados estas. cartesiano en la con la geometría. Identificar ángulos según sus Usa la clasificación de las funciones para hallar Determina el ángulo de referencia para un graficacion de ángulos medidas y características. el conjunto solución a una situación problemica ángulo medido en radianes o grados. Clasifica los ángulos cotidiana. según su medida y la Justifica matemáticamente respuestas con suma de sus medidas. base en las funciones trigonométricas. INDICADORES DE DESEMPEÑO Identifica las características de una función a partir de su expresión analítica Resuelve sistemas de ecuaciones en forma gráfica. Identifica elementos fundamentales en curvas sinusoidales. Calcula la distancia entre dos puntos. CÓDIGO: ANEXOPE1 VERSIÓN: 1 PREGUNTA PROBLEMATIZADORA ¿Cuál es la importancia de los pensamientos espaciales y numéricos en el desarrollo tecnológico de este mundo moderno? Analiza si una ecuación dada representa o no a una circunferencia Grafica parábolas con vértice en (0,0) y en (h, k) Comprende el significado de la directriz en la construcción de una parábola Resuelve problema utilizando el concepto de elipse Grafica hipérbolas conociendo algunos elementos Grafica vectores en el plano y en el espacio. Realiza la adicción y sustracción entre vectores. ÁMBITOS CONCEPTUALES Pensamiento espacial. . ESTRATEGIAS DIDÁCTICAS Socializaciones de las temáticas. Desarrollar ejercicios de grupo e intercambiar e intercambiar los diferentes métodos utilizados en la resolución de problemas con la utilización de razones trigonométricas. Desarrollar ejercicios en los que sea necesario utilizar el transportador y compas para su solución y graficación de figuras con razones trigonométricas. CONTENIDOS La recta La circunferencia Ecuación general de segundo grado en dos variables. La parábola La elipse La hipérbola Traslación de curvas Vectores en el plano y en el espacio. Operaciones con vectores. Operaciones con vectores. Ecuación de la recta y el plano. Concepto de matriz. Adición y sustracción de matrices. CRITERIOS DE EVALUACIÓN Cuaderno (Toma de nota en clase). Participación en clase. Sustentar los ejercicios de clase y/o talleres en el tablero. Participación en los foros y utilizaciones de los medios virtuales. (Blogs, Plataforma, Correo electrónico). Presentación de Trabajos de manera individual o grupal. CÓDIGO: ANEXOPE1 VERSIÓN: 1 ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN Continúa durante los periodos. CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO PERIODO UNDECIMO PRIMERO EJES GENERADORES DISCIPLINAS RELEVANTES Sistemas numéricos, Funciones y Algebra de Funciones Estadística, Calculo ESTÁNDARES COMPETENCIAS Y FORMULACIÓN Y EJECUCIÓN RAZONAMIENTO Y Comparo y contrasto las propiedades de los INTERPRETACIÓN ARGUMENTACIÓN números (Naturales, enteros, racionales y REPRESENTACIÓN reales) y las de sus relaciones y operaciones Comprendo la diferencia entre los Realizo operaciones que Asumo una posición activa en la para construir, manejar y utilizar conjuntos numéricos que involucren las diferentes formas solución de problemas que apropiadamente los distintos sistemas conforman los números reales. de los números reales. involucran números reales. numéricos. Identifico las propiedades entre Manejo las propiedades de Creo un ambiente que permita una funciones hallando el dominio y dominio y rango de funciones en buena comprensión de las rango con facilidad. el plano cartesiano propiedades de una función. Identifico las propiedades del valor absoluto en la solución de inecuaciones. Manejo las propiedades del valor absoluto en la solución de inecuaciones. Creo un ambiente que permita una buena comprensión de las inecuaciones con valor absoluto. Realizo procedimientos afines a Manejo adecuadamente las Creo un ambiente que permita una las diferentes técnicas de conteo diferentes propiedades de buena comprensión de las con el cálculo de probabilidades. distribución probabilística distribuciones de probabilidad INDICADORES DE DESEMPEÑO Argumenta y justifica operaciones con los diferentes conjuntos numéricos. Formula y argumenta las propiedades del valor absoluto en las desigualdades en la solución de Inecuaciones. Grafica en el plano cartesiano, funciones lineales, polinómicas, racionales, radicales y exponenciales de forma clara identificando fácilmente su dominio y rango Formula y justifica los procedimientos afines a las diferentes técnicas de conteo con el cálculo de probabilidades Resuelve de forma acertada las distintas valoraciones de la prueba Pal. Resuelve de forma acertada las distintas valoraciones de la prueba Externa Demuestra interés por las actividades que facilitan el aprendizaje y favorecen el desarrollo de habilidades del pensamiento, por medio de la actitud de escucha, participación y responsabilidad. PREGUNTA PROBLEMATIZADORA ÁMBITOS CONCEPTUALES CONTENIDOS CÓDIGO: ANEXOPE1 VERSIÓN: 1 ¿Cómo aplicar de forma objetiva Pensamiento Sistemas numéricos: “ Desigualdades e inecuaciones” ejercicios y problemas Numérico. Inecuaciones con el valor absoluto matemáticos aplicados y Pensamiento Funciones: Afín, Lineales, Cuadráticas, Polinómicas, Racionales. Radicales, socializados en un contexto métrico Variacional. Exponenciales cotidiano? Estadística descriptiva ESTRATEGIAS DIDÁCTICAS CRITERIOS DE EVALUACIÓN Trabajos a partir de presentaciones video gráficas. Participación en clase. Socializaciones de las temáticas. Presentación de trabajos de manera individual o en grupo Elaboración de carteleras Capacidad de argumentar claramente las actividades realizadas en clase y fuera de ella. Ejercicios de consulta. Sustentación oral, escrita o virtual. Resolución de pruebas escritas Para la entrega de trabajos, por un día de retraso se calificara sobre 3.5 ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN El refuerzo es constante, calificando los procesos del estudiante en la clase, Actividades CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO UNDECIMO EJES GENERADORES Funciones y Algebra de Funciones ESTÁNDARES Analizo las relaciones y propiedades entre las expresiones algebraicas y gráficas de funciones polinómicas y racionales y de sus derivadas. PERIODO SEGUNDO DISCIPLINAS RELEVANTES Estadística, Calculo COMPETENCIAS INTERPRETACIÓN Y REPRESENTACIÓN Comprendo la diferencia entre una Función y el límite de una función. Identifico las propiedades entre límites de una función y sus diferentes estrategias al aplicarlas. FORMULACIÓN Y EJECUCIÓN Grafico Límites de funciones que involucren las diferentes formas de expresarlas en el plano cartesiano. Formulo y explico las reglas de límites, y reconozco cuando es oportuno utilizar cada una de estas en una expresión algebraica, describiendo los procedimientos matemáticos empleados. RAZONAMIENTO Y ARGUMENTACIÓN Asumo una posición activa en la solución de problemas que involucran funciones. Creo un ambiente que permita una buena comprensión de las propiedades del límite de una función. Realizo procedimientos afines a Creo un ambiente que permita una las diferentes técnicas de conteo buena comprensión de las con el cálculo de probabilidades. distribuciones de probabilidad. INDICADORES DE DESEMPEÑO Argumenta de forma acertada operaciones que involucren los límites de una función. Formula correctamente las propiedades que se aplican el en plano cartesiano para construir el límite de una función. Justifica congruentemente los procedimientos afines a las diferentes técnicas usadas en las distribuciones probabilísticas Resuelve de forma acertada las distintas valoraciones de la prueba Pal. Resuelve de forma acertada las distintas valoraciones de la prueba Externa Demuestra interés por las actividades que facilitan el aprendizaje y favorecen el desarrollo de habilidades del pensamiento, por medio de la actitud de escucha, participación y responsabilidad PREGUNTA PROBLEMATIZADORA ¿Cómo aplicar de forma objetiva ejercicios y problemas matemáticos aplicados y socializados en un contexto cotidiano? ESTRATEGIAS DIDÁCTICAS ÁMBITOS CONCEPTUALES Pensamiento Numérico. Pensamiento métrico Variacional. CONTENIDOS Límites: Nociones de Límite Propiedades de los Límites. Limites Laterales, Limites Infinitos. Estadística: Variables Aleatorias, Distribución de Bernoulli, Distribución Binomial CRITERIOS DE EVALUACIÓN CÓDIGO: ANEXOPE1 VERSIÓN: 1 Trabajos a partir de presentaciones video gráficas. Plataforma Educa Ejercicios en la sala virtual y aula talle. Resolución de pruebas escritas Participación en clase. Presentación de trabajos de manera individual o en grupo Capacidad de argumentar claramente las actividades realizadas en clase y fuera de ella. Sustentación oral, escrita o virtual ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN El refuerzo es constante, calificando los procesos del estudiante en la clase, Actividades CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO UNDECIMO EJES GENERADORES Limites ESTÁNDARES Analizo las relaciones y propiedades entre las expresiones algebraicas aplicadas a los límites y gráficas de funciones polinómicas y racionales y de sus derivadas. PERIODO TERCERO DISCIPLINAS RELEVANTES Estadística, Calculo COMPETENCIAS INTERPRETACIÓN Y REPRESENTACIÓN Ejecuto de forma adecuada el proceso de diferenciación para hallar la derivada de una función. Identifico las propiedades entre las derivadas de una función y sus diferentes estrategias al aplicarlas. FORMULACIÓN Y EJECUCIÓN Grafico derivadas de funciones que involucren las diferentes formas de expresarlas en el plano cartesiano. Formulo y explico las reglas de derivación, reconociendo cuando es oportuno utilizar cada una de estas en una expresión algebraica. RAZONAMIENTO Y ARGUMENTACIÓN Asumo una posición activa en la solución de problemas que involucran Derivadas. Creo un ambiente que permita una buena comprensión de las propiedades de derivación en una función. Realizo procedimientos afines a Creo un ambiente que permita una los diferentes modelos buena comprensión modelos estadísticos aplicados en el estadísticos. tiempo. INDICADORES DE DESEMPEÑO Argumenta y resuelve de forma acertada ejercicios donde se aplica la noción de derivadas con límites. Argumenta y resuelve de forma acertada ejercicios donde se aplican las diferentes reglas de derivación. Analiza y resuelve de forma acertada ejercicios donde aplica la regla de la cadena. Formula correctamente las propiedades que se aplican el en plano cartesiano para construir la derivada de una función. Justifica congruentemente los procedimientos afines a las diferentes técnicas aplicadas en un modelo estadístico Resuelve de forma acertada las distintas valoraciones de la prueba Pal. Resuelve de forma acertada las distintas valoraciones de la prueba Externa Demuestra interés por las actividades que facilitan el aprendizaje y favorecen el desarrollo de habilidades del pensamiento, por medio de la actitud de escucha, participación y responsabilidad. PREGUNTA PROBLEMATIZADORA ¿Cómo aplicar de forma objetiva ejercicios y problemas matemáticos aplicados y ÁMBITOS CONCEPTUALES CONTENIDOS Pensamiento Numérico. Pensamiento métrico Variacional. FUNCIONES: Noción de Derivada “Límites” Reglas de derivación. Regla de la Cadena. CÓDIGO: ANEXOPE1 VERSIÓN: 1 socializados cotidiano? en un contexto ESTRATEGIAS DIDÁCTICAS Trabajos a partir de presentaciones video gráficas. Plataforma Educa Ejercicios en la sala virtual y aula talle. Resolución de pruebas escritas Estadística: Distribución Hipergeometrica, Poisson, Modelos Estadísticos. CRITERIOS DE EVALUACIÓN Participación en clase. Presentación de trabajos de manera individual o en grupo Capacidad de argumentar claramente las actividades realizadas en clase y fuera de ella. Sustentación oral, escrita o virtual ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN El refuerzo es constante, calificando los procesos del estudiante en la clase, Actividades CÓDIGO: ANEXOPE1 VERSIÓN: 1 GRADO UNDECIMO EJES GENERADORES Derivadas PERIODO CUARTO DISCIPLINAS RELEVANTES Estadística, Calculo ESTÁNDARES Interpreto la noción de derivada como razón de cambio y como valor de la pendiente de la tangente a una curva y desarrollo métodos para hallar las derivadas de algunas funciones básicas en contextos matemáticos y no matemáticos. COMPETENCIAS INTERPRETACIÓN Y REPRESENTACIÓN Ejecuto de forma adecuada el proceso de diferenciación para hallar la integral definida. Identifico las propiedades entre la integral de una función y sus diferentes estrategias al aplicarlas. FORMULACIÓN Y EJECUCIÓN Grafico integrales que involucren las diferentes formas de expresarlas en el plano cartesiano. Formulo y explico las reglas de integración, reconociendo cuando es oportuno utilizar cada una de estas en una expresión algebraica. RAZONAMIENTO Y ARGUMENTACIÓN Asumo una posición activa en la solución de problemas que involucran integrales. Creo un ambiente que permita una buena comprensión de las propiedades de las integrales en una función. Realizo procedimientos afines a Creo un ambiente que permita una los diferentes modelos buena comprensión modelos estadísticos aplicados en el estadísticos. tiempo. INDICADORES DE DESEMPEÑO Argumenta y resuelve de forma acertada ejercicios donde se aplica la noción de integrales definidas. Argumenta y resuelve de forma acertada ejercicios donde se aplican las diferentes reglas de integración. Analiza y resuelve de forma acertada ejercicios donde aplica derivadas. Formula correctamente las propiedades que se aplican el en plano cartesiano para construir la integral de una función. Justifica congruentemente los procedimientos afines a las diferentes técnicas aplicadas en un modelo estadístico Resuelve de forma acertada las distintas valoraciones de la prueba Pal. Resuelve de forma acertada las distintas valoraciones de la prueba Externa Demuestra interés por las actividades que facilitan el aprendizaje y favorecen el desarrollo de habilidades del pensamiento, por medio de la actitud de escucha, participación y responsabilidad. PREGUNTA PROBLEMATIZADORA ¿Cómo aplicar de forma objetiva ejercicios y problemas matemáticos aplicados y ÁMBITOS CONCEPTUALES CONTENIDOS Pensamiento Numérico. Pensamiento métrico Variacional. Integrales: Aplicaciones de la Derivada. Noción de Integrales. Propiedades de la Integral Definida. CÓDIGO: ANEXOPE1 VERSIÓN: 1 socializados cotidiano? en un contexto ESTRATEGIAS DIDÁCTICAS Trabajos a partir de presentaciones video gráficas. Plataforma Educa Ejercicios en la sala virtual y aula taller. Resolución de pruebas escritas Estadística: Series de tiempo, Diagramas de Paretto y Análisis de Regresión. CRITERIOS DE EVALUACIÓN Participación en clase. Presentación de trabajos de manera individual o en grupo Capacidad de argumentar claramente las actividades realizadas en clase y fuera de ella. Sustentación oral, escrita o virtual ACTIVIDADES DE REFUERZO, SUPERACIÓN Y/O PROFUNDIZACIÓN El refuerzo es constante, calificando los procesos del estudiante en la clase, Actividades 18. BIBLIOGRAFÍA SIEE Lineamientos curriculares del MEN, European Agency for Development in Special Needs Education (2003). Inclusive Education and Classroom Practices- Summary Report. http://www.europeanagency.org/publications/ereports/inclusive-education-and-classroompractices/inclusiveeducation-and-classroom-practices (Consultat de 20 de noviembre de 2008) Plataforma Ciutadana per a una Escola Inclusiva (2006). Horitzó: Escola Inclusiva. Barcelona. www.pangea.org/acpeap/doc%20pdf/horitzo.pdf (Consultat el 18 de julio de 2009) Sanches, I. (2005). Compreender, agir, mudar, incluir. Da investigação-acção à educação inclusiva.Revista Lusófona de Educação, 5, 127-142. 19. INTEGRANTES DEL AREA: PERFIL DOCENTE NOMBRE COMPLETO: TATIANA VANESSA BETANCUR MONTOYA TITULO OBTENIDO Licenciada preescolar en UNIVERSIDAD Y AÑO DE GRADUACIÓN ULTIMOS ESTUDIOS REALIZADOS DESEMPEÑOS FORTALEZAS Corporación Universitaria Lasallista Graduada en el año 2010 Diplomado en evaluación del aprendizaje. Año 2014 Docente de áreas integradas en los grados jardín, transición y segundo. Coordinadora de convivencia por 6 meses en Cubrimiento de licencia de maternidad e incapacidad por cirugía. Líder y participante de equipo de reestructuración del PEI del Colegio La Salle Bello. Se trabajar en equipo. Soy Responsable. Asertiva. Comprometida. Respetuosa. Propositiva. Observadora. manejo adecuado de los conceptos de las áreas que imparto. Manejo y Utilización de las TIC´S. NOMBRE COMPLETO: LILIANA MARÍA ARANGO JARAMILLO TITULO OBTENIDO UNIVERSIDAD Y AÑO DE GRADUACIÓN ULTIMOS ESTUDIOS REALIZADOS DESEMPEÑOS FORTALEZAS Licenciatura en Educación Preescolar Corporación Universitaria Lasallista de Medellín 1995 Diplomado en Ambientes Virtuales de Aprendizaje. ( Corporación Universitaria Lasallista) Diplomado en comprensión lectora. ( Universidad Javeriana) Docente de áreas integradas grado 1°. Docente del área de matemáticas 3°B- 3°C. Docente de Ciencias Naturales 4°B- 4°C. Trabajo en equipo Responsabilidad Creatividad Capacidad para resolver dificultades Capacidad de liderazgo en proyectos institucionales Acompañamiento permanente a los estudiantes Buenas relaciones interpersonales. NOMBRE COMPLETO: ANA MILENA CANO RESTREPO TITULO OBTENIDO UNIVERSIDAD Y AÑO DE GRADUACIÓN ULTIMOS ESTUDIOS REALIZADOS DESEMPEÑOS FORTALEZAS LICENCIATUR A EN EDUCACIÓN BÁSICA EN ENFASIS EN MATEMÁTICA S TECNOLOGIC O DE ANTIOQUIA INSTITUCIÓN UNIVERSITARI A 2008 DIPLOMADO EN DOCENCIA UNIVERTARIA 2011 ESAP. (MANIZALEZ) EL CARMELO 2014. PRIMARIA I. E. DE JESUS 2010 – 2013 BACHILLERATO I.E MARIANO DE J. VILLEGAS BACHILLERATO ESCUCHO CORRECCIONES Y CONSEJOS. NOMBRE COMPLETO: JUAN MANUEL ALZATE CANO TITULO OBTENIDO Licenciado en Educación Básica con énfasis en Matemáticas UNIVERSIDA D Y AÑO DE GRADUACIÓ N Fundación Universitaria Luis Amigo. Medellín, 2007. ULTIMOS ESTUDIOS REALIZADOS DESEMPEÑOS FORTALEZAS Diplomado en Sistematización de Experiencias Educativas Soy una persona activa y planificadora de rutinas de trabajo académicas. Buen Manejo en las Herramientas tecnológicas y ofimáticas, plataformas interactivas. Trabajo en equipo, Buen conocimiento de la disciplina y conceptos propios del área. Organizado, Planificador, Creativo, Innovador. NOMBRE COMPLETO: GLORIA LILIANA CASTAÑO VÁSQUEZ TITULO OBTENIDO Licenciada en Educación Básica con énfasis en Matemáticas e Informática UNIVERSIDA D Y AÑO DE GRADUACIÓ N Universidad Cooperativa de Colombia 10 de Mayo 2012 ULTIMOS ESTUDIOS REALIZADOS DESEMPEÑOS Diplomado en Sistematización de Experiencias Educativas Titular 7 C Docente Matemáticas 7 B, 7C, 8 ABC FORTALEZAS Responsabilidad en el desarrollo de las actividades Creatividad Conocimiento del área Control de grupo Trabajo en equipo Adaptación al cambio. de NOMBRE COMPLETO: ARNALDO JOSÉ MANCHEGO PEREZ TITULO OBTENIDO UNIVERSIDAD Y AÑO DE GRADUACIÓN ULTIMOS ESTUDIOS REALIZADOS DESEMPEÑOS FORTALEZAS Licenciado en educación Física Recreación y deporte – Nivel Básica. Politécnico colombiano Jaime Isaza Cadavid 2008. Homologando licenciatura en matemáticas e informática (7°semestre). Docente de Matemáticas Y Física 9°A,B,C y 10° A,B. Especialista en Lúdica Educativa Juan D castellanos Tunja Boyacá2007 Conocimiento del saber especifico del área. Responsabilidad. Sentido de Pertenencia. Universidad cooperativa de Colombia 2013 NOMBRE COMPLETO: IVAN ANDRES GIRALDO SALGUERO TITULO OBTENIDO Matemático UNIVERSIDA D Y AÑO DE GRADUACIÓ N Univ. Nacional 2010 ULTIMOS ESTUDIOS REALIZADOS DESEMPEÑOS FORTALEZAS Diplomado tic`s, Diplomado Pedagogía Jefe de Área Matemáticas Docente de Cálculo en 11º y Trigonometría grados 10º. Responsable del Área de mejora No.1 de “Mediciones” en en Conocimiento del área Liderazgo, Proactivo, Fraternidad. 20. CONTROL DE CAMBIOS DEL PLAN DE ÁREA CONTROL DE CAMBIOS Numeral Modificado Modificación Efectuada Versión 1 REVISÓ: Grupo del Distrito APROBÓ: VIGENTE DESDE: FIRMA: FIRMA: 4 de Abril 2013