Actividad_individual_de_la_unidad_3

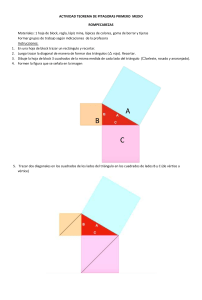
Actividad individual
En la jornada de práctica anterior, se aplico la siguiente actividad en el grupo de
3° “A”, en la Escuela Secundaria General “18 de marzo”, ya que el tema trabajado
fue “El Teorema de Pitágoras” del bloque II. El contenido de esta actividad es “.
Análisis de las relaciones entre las áreas de los cuadrados que se construyen
sobre los lados de un triángulo rectángulo.
Nombre: “Jardines cuadrados”
Objetivos de aprendizaje perseguidos:
Para esta actividad se pretende que los alumnos determinen las relaciones
entre las áreas de los cuadrados construidos sobre los lados de un triángulo
rectángulo, mediante la superposición de superficies y el cálculo de áreas.
Descripción de la manera en que se desarrolla la actividad de aprendizaje
en clase para que cumpla con estos objetivos.
La actividad es de tipo individual, con el objetivo de que cada estudiante desarrolle
los conocimientos necesario que le ayuden a resolver problemas relacionados con
el teorema de Pitágoras.
El primer paso es construir en una hoja dos cuadrados tomando como base las
medidas de los lados menores del siguiente triangulo (es necesario que los
alumnos se den cuenta que es un triángulo rectángulo isósceles).
5 cm
5 cm
Enseguida deben trazar una diagonal en cada cuadrado que construyeron,
recorten las figuras resultantes y con éstas intenten cubrir el cuadrado trazado en
el lado mayor.
Alumna: Elsa Rodríguez Segura
Nº L: 26
Este es el cuadro que tienen que
rellenar con los dos cuadrados
formados o dibujados con las medidas
de los dos lados menores (catetos)
Posteriormente y después de la realización de los trazos, recortes y pegados
necesarios se contestaran las siguientes preguntas:


¿Con las figuras recortadas lograron cubrir toda la superficie del cuadrado
mayor? ¿Por qué crees que sucede esto?
¿Qué clase de triángulo es el que está sombreado?
La actividad se lleva a cabo paso por paso y siempre procurando trabajar a un
mismo rito, resolviendo dudas, y tratando de fomentar la participación activa de los
estudiantes para que poco a poco construyan su conocimiento de manera
autónoma. Al hacer el corte de los cuadrados dibujados, los alumnos podrán
identificar que la suma de los cuadrados de los dos lados pequeños (catetos) es
igual al área del cuadrado mayor (el correspondiendo al cuadrado de la
hipotenusa) cumpliéndose de esta manera el teorema de Pitágoras.
Describa cuál es la estructura de su materia lógico abstracto
La asignatura de matemáticas es de cierto modo lógica-abstracta-concreta, porque
se siguen una serie de pasos ejecutando operaciones y demás procedimientos
que intentan comprobar un hecho o fenómeno, de manera real, que a veces tiene
explicación pero que otras no. En su mayoría de los fenómenos que se resuelven
son concretos porque existe una respuesta fija y determinada por una serie de
experimentos y demostraciones, que comprueban la teoría planteada.
Alumna: Elsa Rodríguez Segura
Nº L: 26
Identificar si son hechos abstractos y /o concretos
Son abstractos los conceptos o teorías que se manejan porque realmente
demuestran un fenómeno, pero no se está totalmente comprobado, los resultados
obtenidos son meras aproximaciones.
Son a veces concretos cuando la teoría está totalmente comprobada y tiene
veracidad, ahí es cuando no se tiene duda de que el resultado sea real y
verdadero.
Plantee cuales podrían ser las variaciones que se podrías implementar en
la actividad elegida.
Una de las variaciones que se puede realizar al problema, es que la situación se
contextualice, es decir se plantee como un problema real, por ejemplo: Se van a
construir 3 plazas cuadradas adyacentes a los límites de un jardín, como el que
aparece en el dibujo, tomando como base las medidas de sus lados. Donde a
partir de los cálculos necesarios, deben contestar analíticamente las siguientes
preguntas.
¿Cuánto mide el área de cada una de las plazas?
Encuentren qué relaciones hay entre las áreas de las3
plazas.
¿Qué figura geométrica representa el jardín?
Esta respuesta debe ser justificada con base a la descripción de la
actividad y considerando su realidad dentro de la institución en la que
labora.
En referencia a este punto creo que la problemática planteada debe estar
contextualizada, para que los alumnos no solo se enseñen a hacer una
mecanización de los ejercicios, sino que además, analicen las problemáticas y
puedan aplicar los conocimientos necesarios para resolverla. L actividad, puede
realizarse con el trazo y corte de papel, como se especificó en un principio.
Alumna: Elsa Rodríguez Segura
Nº L: 26