iii bgu física - prof. juan ponce

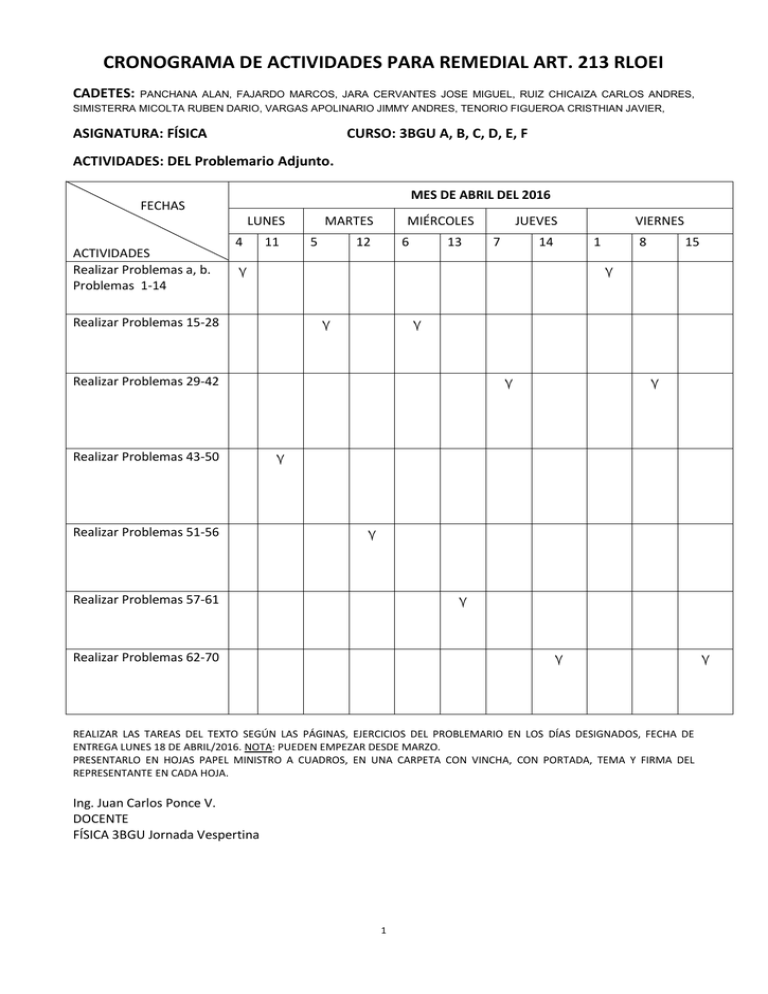
CRONOGRAMA DE ACTIVIDADES PARA REMEDIAL ART. 213 RLOEI
CADETES:
PANCHANA ALAN, FAJARDO MARCOS, JARA CERVANTES JOSE MIGUEL, RUIZ CHICAIZA CARLOS ANDRES,
SIMISTERRA MICOLTA RUBEN DARIO, VARGAS APOLINARIO JIMMY ANDRES, TENORIO FIGUEROA CRISTHIAN JAVIER,
ASIGNATURA: FÍSICA
CURSO: 3BGU A, B, C, D, E, F
ACTIVIDADES: DEL Problemario Adjunto.
MES DE ABRIL DEL 2016
FECHAS
LUNES
ACTIVIDADES
Realizar Problemas a, b.
Problemas 1-14
4
11
MARTES
5
MIÉRCOLES
12
6
13
JUEVES
7
14
۷
۷
8
15
۷
۷
Realizar Problemas 29-42
Realizar Problemas 51-56
1
۷
Realizar Problemas 15-28
Realizar Problemas 43-50
VIERNES
۷
۷
۷
۷
Realizar Problemas 57-61
۷
Realizar Problemas 62-70
REALIZAR LAS TAREAS DEL TEXTO SEGÚN LAS PÁGINAS, EJERCICIOS DEL PROBLEMARIO EN LOS DÍAS DESIGNADOS, FECHA DE
ENTREGA LUNES 18 DE ABRIL/2016. NOTA: PUEDEN EMPEZAR DESDE MARZO.
PRESENTARLO EN HOJAS PAPEL MINISTRO A CUADROS, EN UNA CARPETA CON VINCHA, CON PORTADA, TEMA Y FIRMA DEL
REPRESENTANTE EN CADA HOJA.
Ing. Juan Carlos Ponce V.
DOCENTE
FÍSICA 3BGU Jornada Vespertina
1
۷
UNIDAD EDUCATIVA LICEO NAVAL
“CMDTE. RAFAEL ANDRADE LALAMA”
GUAYAQUIL - ECUADOR
PROBLEMARIO PARA EL EXAMEN REMEDIAL_2015
FISICA_3ERO BGU_TODOS
“Porque hay un solo Dios, y también un solo Mediador entre Dios y los hombres, Cristo Jesús hombre, quien Se dio a sí
mismo en rescate por todos, testimonio dado a su debido tiempo”. (1Timoteo 2:5,6)
"En ningún otro hay salvación, porque no hay otro nombre bajo el cielo dado a los hombres, en el cual podamos ser
salvos." (Hechos 4:12)
PROFESOR: Ing. Juan C. Ponce V.
TERCERO BACHILLERATO BGU:”A” ”B” ”C” ”D” ”E” ”F
a.
JORNADA: Vespertina
Identifica con una (x) la unidad fundamental con que se mide cada una de las siguientes cantidades.
Joule
Rad/s
Dina-s;
N-s
Km/s
m/s
N,
Dina
N-m
Dina-cm
Vib/s
(Hz)
Rad/m
Rad/cm
s
hora
cm/s2
m/s2
Kg,
g
m
cm
km
g-cm/s;
kg-m/s
Cantidad de
movimiento
Torque
Aceleración
Rapidez angular
Impulso
Número de onda
Distancia,
Desplazamiento
Tiempo, periodo
Frecuencia
Energía, trabajo
Velocidad
Masa
Fuerza
b. Determina si son verdaderas (V) o falsas (F) las siguientes proposiciones.
Si la frecuencia de un sonido es alta, tendremos un tono grave………….. (
)
La fuerza gravitacional entre dos cuerpos es directamente proporcional al cuadrado de la distancia que los
separa…... ( )
c. Cuando un conductor hace sonar la bocina de su vehículo para alertar a un peatón distraído, el sonido
percibido por esta persona será cada vez más agudo……………………….. (
)
d. Tenemos tonos agudos cuando la longitud de onda del sonido es corta……………….… ( )
e. Si la frecuencia de un sonido es baja, tendremos un tono agudo………. ( )
f. Cuando la longitud de onda de un sonido es larga, su tono es grave……….… ( )
g. Cuando alguien de nosotros nos alejamos rápidamente de una fuente sonora estacionaria (reposo),
percibiremos un sonido cada vez más grave……….… ( )
h. La intensidad de cualquier sonido está relacionado con la frecuencia del mismo…….. ( )
i. Cuando una orquesta sinfónica realiza su presentación, distinguimos cada instrumento por su respectivo
timbre……… ( )
j. La explosión de una bengala produce un sonido agudo y débil……… ( )
k. El movimiento relativo entre una fuente ondulatoria y un receptor producirá un cambio en la frecuencia
observada por el receptor y este fenómeno se llama Efecto Doppler…… ( )
l. Si la colisión es completamente elástica, la energía cinética total antes del choque es igual a la energía
cinética total justamente después………….. (
)
m. Cuando el centro de gravedad de un sistema se ubica por debajo del punto de apoyo, tiene un equilibrio
inestable……………………….. ( )
n. La conservación de la cantidad de movimiento, no es deducida de las leyes de Newton……………….… ( )
a.
b.
2
o.
r.
s.
t.
u.
El torque es una capacidad que tiene una fuerza cuando puede hacer rotar un cuerpo alrededor de un punto
fijo………. ( )
En una colisión completamente inelástica, parte de la energía cinética se transforma en calor debido a que
los cuerpos quedan adheridos después del choque……….… ( )
Para que un sistema tenga un equilibrio estable, su centro de gravedad se ubicará por debajo del punto de
apoyo……….… ( )
En una colisión imperfectamente elástica, un cuerpo rebota con mayor rapidez…….. ( )
Cuando un cuerpo o sistema cambia de velocidad, es porque actuó un impulso……… ( )
En las explosiones no se puede aplicar la conservación de la cantidad de movimiento……… ( )
El centro de gravedad, es el punto donde la fuerza gravitacional está concentrada…… ( )
v.
Todos los planetas giran alrededor del sol describiendo orbitas elípticas, siendo el sol uno de los focos. (
p.
q.
RESUELVA LAS SIGUIENTES SITUACIONES PROBLEMAS.
EQUILIBRIO DE SÓLIDOS
1.
Calcule la torca alrededor del eje A en la figura adjunta, debida a
cada una de las fuerzas que se muestran. Sol.: 0,45 N-m
2.
Una viga horizontal uniforme con una longitud de 8.00 m y un peso de 200 N se une a
una pared mediante una junta articulada. Su extremo lejano esta sostenido mediante
un cable que forma un ángulo de 53.0° con la viga (figura adjunta). Una persona de
600 N está de pie a 2.00 m de la pared. Encuentre la tensión en el cable así como la
magnitud y dirección de la fuerza que ejerce la pared en la viga.
Sol.: T= 313N; R= 580N; Ø= 71.1°
3.
Calcule FA y FB para la viga que se representa en la figura mostrada. Las
fuerzas descendentes representan los pesos de maquinaria sobre la viga.
Suponga que la viga es uniforme y tiene una masa de 280 kg y la aceleración
de la gravedad g = 10 m/s2. Sol.: FA = 6300 N; FB = 6100 N
4.
Un sube y baja consiste de un tablón uniforme de masa M y longitud 𝑙 que
sostiene en reposo a un padre y su hija con masas
𝑚𝑓 y 𝑚𝑑
respectivamente,
como se muestra en la figura 12.8. El soporte (llamado punto de apoyo) está
bajo el centro de gravedad del tablón, el padre a una distancia d del centro y
la hija a una distancia 𝑙/2 del centro.
a) Determine la magnitud de la fuerza hacia arriba n que ejerce el soporte
sobre el tablón.
Sol.: 𝒏 = (𝒎𝒇 + 𝒎𝒅 + 𝑴)𝒈
b) Determine donde se debe sentar el padre para equilibrar el sistema en reposo.
𝒎
𝟏
Sol.: 𝒅 = (𝒎𝒅) 𝟐 𝒍
𝒇
5.
La viga horizontal de la figura mostrada pesa 150 N, y su centro de gravedad está en su
centro. Calcule: a) La tensión en el cable, y b) Las componentes horizontal y vertical de
la fuerza ejercida por la pared sobre la viga.
Sol.: a) 625N; b) RX= 500N; RY= 75N
3
)
10 N
6.
Para el sistema mostrado ¿Cuál es el torque resultante con respecto al punto
30 N
2m
O? Sol.: 50 N-m
1m
O
20 N
7.
Un trampolín de 3.00 m de longitud se apoya en un punto a 1.00 m del
extremo fijo, y una clavadista que pesa 500 N se para en el extremo
libre (figura 11.24). El trampolín tiene sección transversal uniforme y
pesa 280 N. Calcule a) la fuerza en el apoyo; b) la fuerza en el
extremo fijo.
RPTA.: a) 1920N; b) 1140N
30 N
8.
9.
Para el sistema mostrado, la magnitud de la fuerza resultante y la suma de las
torcas con respecto al punto O respectivamente son. SOL.: 0 N; 60 N-m
30 N
Calcular la tensión en cada cuerda de las figuras mostradas, si el peso
suspendido es de 2000 N.
Sol:
TA = 1464,1 N
TB = 1793,2 N
TC = 2000N
2m
O
TA = 5464,1 N
TB = 6692,1 N
TC = 2000 N
10.
Un tiburón de 10000 N esta sostenido mediante un cable unido a una barra de
4.00 m que se articula en la base. Calcule LA TENSIÓN en la soga entre la
barra y la pared, si supone que la misma sostiene el sistema en la posición que se
muestra en la figura adjunta. Encuentre LAS FUERZAS HORIZONTAL Y
VERTICAL que se ejercen sobre la base de la barra. IGNORE EL PESO DE LA
BARRA. Sol.: 5077,13 N; Rx = 4770,9 N Ry = 8263,52 N
11.
En la figura adjunta, un motor de peso w cuelga de una cadena unida mediante un
anillo O a otras dos cadenas, una sujeta al techo y la otra a la pared. Calcule las
tensiones en las tres cadenas en términos de w. Los pesos de las cadenas y el
anillo son despreciables. Sol.: 𝑻𝟏 = 𝒘 ; 𝑻𝟐 = 𝟎, 𝟓𝟕𝟕 𝒘 ; 𝑻𝟑 = 𝟏, 𝟏𝟓𝟓 𝒘
4
12.
Encuentre la tensión en los dos alambres que soportan el semáforo de la figura.
Tomando el valor para la aceleración de la gravedad como g = 10 m/s2. Sol.: 330
N; 263,55 N; 198,60 N
IMPULSO Y CANTIDAD DE MOVIMIENTO (ÍMPETU O MOMENTO LINEAL)
13.
El momento lineal de un automóvil de 1500 kg es igual al de un camión de 5000 kg que viaja con una rapidez de
25 millas/h. ¿Cuál es la rapidez del automóvil? Sol.: 83,33 millas/h.
14. Una partícula de 3kg tiene una velocidad de (2i – 4j) m/s. Calcule las componentes de su cantidad de
movimiento y la magnitud son respectivamente.
𝒎
𝒎
Sol.: 𝒑𝒙 = 𝟔 𝒌𝒈. ; 𝒑𝒚 = −𝟏𝟐 𝒌𝒈. ; 𝒑 = 𝟏𝟑, 𝟒 𝒌𝒈. 𝒎/𝒔
𝒔
15.
𝒔
Sobre un bloque de 10 kg se aplica una fuerza F tal como se muestra en la figura.
Si el bloque se mueve en línea recta y parte del reposo. ¿Cuál es la rapidez que
tiene el objeto en t = 4s?
Sol.: 4 m/s
16. Una piedra de 2.00 kg se desliza hacia la derecha por una superficie horizontal
sin fricción a 5.00 m/s, cuando de repente es golpeada por un objeto que ejerce
una gran fuerza horizontal sobre ella por un breve lapso. La gráfica en la figura
8.34 indica la magnitud de esa fuerza como función del tiempo.
a) ¿Qué impulso ejerce esa fuerza sobre la piedra?
b) Calcule la magnitud y dirección de la velocidad de la piedra inmediatamente
después de que la fuerza deja de actuar si esa fuerza actúa i) hacia la
derecha o ii) hacia la izquierda.
Sol.: a) 2.50 N⋅ s; b.i) 6.25 m/s hacia la derecha; b.ii) 3.75 m/s hacia la
derecha.
17.
En la figura adjunta se muestra una curva fuerza–tiempo estimada para una
pelota de béisbol golpeada por un bate. A partir de esta curva, determine a)
el impulso entregado a la pelota, b) la fuerza promedio ejercida sobre la
pelota y c) la fuerza máxima que se ejerce sobre la pelota.
a) 13,5 N.s b) 9 000 N y c) 18 000 N
18. Una bola de tenis de 0,1 kg lleva una velocidad de 25 m/s hacia la derecha,
golpea una raqueta y rebota con la misma rapidez. Si el tiempo de tope entre la bola y raqueta es de 0,04
segundos. ¿Cuál es la fuerza media que realiza la BOLA SOBRE LA RAQUETA? Sol.: 125 N
19. Una pelota de 0.3 kg que se mueve a lo largo de una recta, tiene una velocidad de 5𝑖 [𝑚/𝑠]. La pelota choca
contra una pared y rebota con una velocidad de −3𝑖 [𝑚/𝑠]. Obtenga a) el cambio en su cantidad de movimiento y
b) la fuerza promedio ejercida sobre la pared, si la pelota permanece en contacto con la misma durante
5 × 10−3 [𝑠]. Sol.: a)
𝒎
−𝟐, 𝟒𝟎𝒊 [𝒌𝒈. 𝒔 ]
b)
𝟒𝟖𝟎 𝒊 𝑵
20. La magnitud de la fuerza neta que se ejerce en la dirección x sobre una
partícula de 2,50 kg varia en el tiempo como se muestra en la figura adjunta.
Encuentre: a) el impulso de la fuerza, b) la velocidad final que logra la
partícula si originalmente está en reposo, c) su velocidad final si su velocidad
original es – 2,00 m/s y d) la fuerza promedio ejercida sobre la partícula
durante el intervalo de tiempo entre 0 y 5,0 s. Sol.: a) 12,0 N-s; b) 4,80
m/s; c) 2,80 m/s; d) 2,40 N
5
CONSERVACIÓN DE LA CANTIDAD DE MOVIMIENTO (ÍMPETU O MOMENTO LINEAL) & COLISIONES.
21.
Un tirador sostiene holgadamente un rifle de masa 𝑚𝑅 = 3,0 𝑘𝑔, de manera que pueda retroceder libremente
al hacer un disparo. Dispara una bala de masa 𝑚𝐵 = 5,0 𝑔 con una velocidad horizontal relativa al suelo de
𝑣𝐵𝑥 = 300 𝑖 (𝑚/𝑠) ¿Qué velocidad de retroceso 𝑣𝑅𝑥 tiene el rifle? ¿Qué momento lineal y energía cinética
finales tiene la bala? ¿Y el rifle? Sol.: - 0.50 i m/s; para la bala: 1.50 kg-m/s; 225 J; para el rifle:
1.50 kg-m/s; 0.375 J
22. Un niño de 40 Kg que está parado sobre un estanque congelado lanza una piedra de 2kg hacia el Este, con una
rapidez de 5 m/s. Despreciando la fricción entre el niño y el hielo, calcule la velocidad de retroceso del niño.
Sol.: - 0.25 m/s
23. Se colocan dos bloques de masas M y 3M sobre una superficie horizontal sin
fricción. Entre ellas se sujeta un resorte ligero y los bloques se empujan para
acercarlos, con el resorte entre ellos (ver figura). Se quema una cuerda que
mantiene a los bloques unidos, después de lo cual, el de 3M se mueve hacia la
derecha con una rapidez de 2m/s. ¿Cuál es la rapidez del bloque de masa M?
(suponga que se encuentran inicialmente en reposo).
a)
2m/s b) 4m/s c) 6m/s d) 10m/s
e) 5,50 m/s
24. Una bomba que está INICIALMENTE EN REPOSO explota formando tres fragmentos iguales. Las
velocidades de dos de los fragmentos son 3𝑖 + 2𝑗[𝑚/𝑠] y (−𝑖 − 3𝑗)[𝑚/𝑠]. ¿Cuál es la velocidad del tercer
fragmento? Justifique su respuesta.
a) (3i  2 j )[m / s] ; b)
(i  j )[m / s]
; c)
(2i  j )[m / s] ;
d)
(i  3 j )[m / s] ; e) ninguna
25. Sobre una superficie horizontal y sin fricción, un objeto, inicialmente en reposo, estalla en tres partes
idénticas. ¿Cuál de las figuras que se incluyen abajo representa mejor el fenómeno después de la explosión?
a)
b)
c)
d)
v0
v  0
v0
e)
v0
26. Un bloque en reposo de 2 kg explota y se rompe en dos
partes como se muestra en la figura. Encontrar la rapidez
final de la masa más pesada. Sol.: 0,167 m/s
27. Dos vehículos de 2000 kg y 1500 kg de masa, SE DESPLAZAN EN LA MISMA DIRECCIÓN PERO EN
SENTIDO CONTRARIO, con rapideces de 108 km/h y 72 km/h RESPECTIVAMENTE. Después de colisionar y
suponiendo que AMBOS QUEDAN UNIDOS, ¿cuál será la velocidad del conjunto? Sol.: 8,57 m/s, en
dirección del vehículo de 2000 kg.
6
28. En el cruce de la Avenida 9 de Octubre y Boyacá, un auto subcompacto
amarillo de 950 kg que viaja al este por Boyacá choca con una camioneta
pickup color rojo de 1900 kg que viaja al norte por la Avenida 9 de Octubre
y se pasó el alto de un semáforo (ver figura). Los dos vehículos quedan
pegados después del choque, y se deslizan a 16.0 m/s en dirección 24.0° al
este del norte. Calcule la rapidez de cada vehículo antes del choque. El
choque tiene lugar durante una tormenta; las fuerzas de fricción entre los
vehículos y el pavimento húmedo son despreciables.
Sol.: auto amarillo = 19.5 m/s; camioneta pickup = 21.9 m/s
29. Dos autos de la misma masa, se mueven con igual rapidez, chocan en una esquina de dos calles perpendiculares,
y continúan moviéndose unidos después del choque. Si la rapidez original de ambos era de 60 km/h, ¿cuál es el
valor de la velocidad de los autos después del choque? Justifique su respuesta. a) 20 km/h b) 42 km/h c)
30 km/h d) 15 km/h e) ninguna.
30. Un pez de 5 kg que nada a 1 m/s se traga un pez
distraído de 1 kg que está en reposo. ¿Cuál es la
rapidez del pez grande inmediatamente después del
almuerzo? ¿Cuál sería su rapidez si el pequeño pez
hubiera estado nadando hacia él a 4 m/s?
Sol.: 0,833 m/s; 0,17 m/s
MOVIMIENTO CIRCULAR UNIFORME (M.C.U.) Y FUERZA CENTRÍPETA
31.
Una piedra atada a una cuerda describe una circunferencia de 1,5 m de radio, recorriendo 25 revoluciones en
un minuto. Encuentre: (a) la rapidez angular; (b) la rapidez tangencial; (c) la aceleración centrípeta. Sol.: (a)
2.62 rad/s; (b) 3.93 m/s; (c) 10.3 m/s 2.
32. El movimiento rotacional de la tierra lo ejecuta en 24 horas. (a) Calcular el desplazamiento angular de un
punto del Ecuador en 6 horas; (b) encuentre la rapidez tangencial en dicho punto, si el radio ecuatorial es de
6378 km. Sol.: (a) 1,57 rad; (b) 463,6 m/s.
33. La luna da una revolución completa alrededor de la tierra en un periodo de 27,32 días. Si la distancia Tierra –
Luna es
3,82  108 m (a) calcule la rapidez lineal; (b) ¿cuál es la rapidez angular?; (c) encuentre la aceleración
centrípeta. Sol.: (a) 1016,32 m/s; (b) 𝟐, 𝟔𝟔 × 𝟏𝟎−𝟔 𝒓𝒂𝒅/𝒔; (c) 𝟐, 𝟕𝟎 × 𝟏𝟎−𝟑 𝒎/𝒔𝟐
34. Un ciclista recorre una pista circular de 20 m de radio a razón de 0,5 rad/s durante 5 min. Calcule (a)
aceleración centrípeta; (b) rapidez lineal; (c) desplazamiento angular; (d) las revoluciones que da el ciclista; (e)
el espacio que recorre; (f) la frecuencia y período. Sol.: (a) 5 m/s2; (b) 10 m/s; (c) 150 rad; (d) 23,89
rev; (e) 3000 m; (f) 0,08 rev/s ; 12,5 s.
35. Un cuerpo recorre un círculo de 40 cm de radio, describiendo un ángulo de 3 radianes en 2 segundos. Calcule:
(a) su rapidez angular; (b) su rapidez tangencial; (c) su periodo; (d) su frecuencia. Sol.: (a) 1,5 rad/s; (b)
0,6 m/s; (c) 4,17 s; (d) 0,24 rev/s.
36. Un equipo de sonido dispone de un plato de tocadiscos que gira con una rapidez angular de 45 rpm. Se coloca
una moneda de 20 gramos en el plato que gira con él, a una distancia de 5 cm del eje. a) Calcule la aceleración
centrípeta de la moneda; b) ¿cuál es la rapidez lineal de la misma?; c) halle la fuerza de rozamiento que actúa
sobre la moneda; d) identifique las fuerzas que actúan sobre la moneda; e) ¿Qué fuerza actúa como fuerza
centrípeta? Sol.: a) 1,11 m/s2 ; b) 0,2355 m/s; c) 2,22x10-2 N
37. Una persona que tiene una masa de 80 kg está situada en el Ecuador, describe una circunferencia de
aproximadamente 6378 km de radio en un día. Calcule la fuerza centrípeta. Sol.: 2,70 N
7
38. Un avión en maniobras, describe un circulo vertical de 500 m de radio, con una rapidez de 360 km/h. Sabiendo
que la masa del piloto es igual a 70 kg. A) calcule la fuerza que realiza el asiento sobre el piloto, en el punto
más alto de su trayectoria; b) calcule la fuerza que realiza el asiento sobre el piloto, en el punto más bajo de
su trayectoria. Sol.: a) 714 N ; b) 2086 N
39. Un camión tiene un peso de 78400 N, está desplazándose por una vía y tiene que recorrer un parque circular
de 100 m de radio, a una rapidez de 36 km/h. Calcule la fuerza de fricción que realizan los neumáticos contra
el pavimento al dar la curva. Sol.: 8000 N
40. Un automóvil entra en una curva de 100 m de radio, con una rapidez de 36 km/h. Calcule la inclinación que
debe tener el peralte para que se produzca la misma fuerza sobre cada neumático. Sol.: 5,83º
41.
Una masa 𝑚1 sobre una mesa sin fricción está sujeta a otra
masa 𝑚2 que cuelga por medio de una cuerda a través de un
orificio en la mesa (ver figura). Determine las condiciones (en
v y R) con las que debe girar
𝒗𝟐
reposo. Sol:
𝑹
=
m1
para que
m2
quede en
𝒎
( 𝟐) 𝒈
𝒎𝟏
42. En un parque de diversiones, la gente entra en un gran cilindro que puede girar. Cuando la
rapidez alcanza determinado valor, el piso que está debajo de la persona se abre hacia
R
abajo dejando ver un profundo abismo. La persona no cae sino que permanece clavado
contra la pared del cilindro. Encuentre el coeficiente de fricción estático necesario para
impedir su caída. Sol.:
𝝁𝑺 =
𝒈𝑹
𝒗𝟐
43. Como se muestra en la figura adjunta, un cascaron cilíndrico de radio r gira con una
rapidez angular 𝜔. Un bloque de madera se recarga en la superficie interior y gira
con él. Si el coeficiente de fricción entre el bloque y la superficie es 𝜇𝑠 , ¿con qué
rapidez angular debe girar el cascarón para que el bloque no resbale y caiga? Suponga
𝑟 = 150 𝑐𝑚 𝑦 𝜇𝑠 = 0,30 Sol.: 4,70 rad/s
44. Como se muestra en la figura adjunta, una pelota B está amarrada a un extremo de
un cordel de 24 cm longitud, y el otro extremo se encuentra sujeto a un punto fijo
O. la pelota se mueve en un círculo horizontal como se muestra. Encuentre la
rapidez tangencial de la pelota en su trayectoria circular si el cordel forma un
ángulo de 30° con la vertical. Sol.: 0,82 m/s
GRAVITACIÓN UNIVERSAL.
45. Una señorita y un joven, tienen una masa de 50 kg y 60 kg respectivamente, los que se encuentran distantes
10 cm. Calcule la fuerza de atracción entre los jóvenes. Sol.: 2x10-5 N
46. Dos neutrones tienen una masa de 1.67x10-27 kg cada uno, se encuentran separados de sus centros a 1x10-12 m.
a) calcule la atracción gravitacional entre ellos; b) ¿cuál es su peso del neutrón en la Tierra? Sol.: a)
1,86x10-40 N; b) 1,64x10-26 N
8
47. Dos masas de 10 kg y 20 kg se atraen con una fuerza de 5x10-5 N. calcule la distancia en que se encuentran.
Sol.: 1.63x10-2 m
48. El sol tiene una masa equivalente a 333000 veces la masa de la tierra, cuya distancia a la tierra es de 1,5x10 8
km, la misma que tiene una masa de 5,98x1024 kg. ¿Cuál es la fuerza de atracción entre estos dos cuerpos
celestes? Sol.: 3,50x1022 N
49. Calcular la aceleración de la gravedad en la superficie de la luna, cuya masa es 7,3x10 22 kg, si tiene un radio de
1,7x103 km aproximadamente. Sol.: 1.68 m/s2
50. Un satélite artificial describe una órbita circular alrededor de la tierra a una altura de 1600 km sobre la
superficie de la misma, si tomamos el valor del radio 6400 km. Calcule el periodo de revolución del satélite.
Sol.: 1,97 h
51. Se dispone un satélite estacionario Intelsat, muy usado en las comunicaciones mundiales, el mismo que gira
junto a la tierra cuyo periodo de revolución es igual al de la tierra, 24 h; el satélite está ubicado sobre el
mismo lugar de la tierra; por tal motivo, un observador desde la superficie terrestre le parecerá que esta
inmóvil. A) calcule la altura en que se encuentra el satélite; b) ¿Cuál es su rapidez de salida? Sol.: a)
35850,47 km; b) 3,073x103 m/s
MOVIMIENTO ONDULATORIO.
52. Un estudiante golpea el agua de una cubeta 4 veces por segundo y observa que la onda producida recorre 60
cm en 5 segundos, ¿cuál es la longitud de onda? Sol.: 3 cm
53. Un diapasón hace vibrar el aire de un tubo sonoro en donde las ondas sonoras viajan a la rapidez de 340 m/s.
Si la longitud de onda es de 20 cm, ¿cuál es la frecuencia del diapasón? Sol.: 1700 Hz
54. Una emisora tiene una frecuencia de 98 MHz de salida al aire, ¿qué longitud de onda electromagnética genera
la misma en el aire? (v = 3x10 8 m/s ; 1Mhz = 106 Hz)
Sol.: 3,06 m
55. Se emite un sonido con una frecuencia de 256 Hz, el mismo que se propaga por tres diferentes medios: a) en
el aire a 340 m/s; b) en el agua a 1450 m/s; y c) en el vidrio a 5000 m/s. ¿Cuál es la longitud de onda del
sonido en cada medio?, ¿Cuál es el periodo en cada medio? Sol.: a) 1,33 m; 3,9x10-3 s; b) 5,66 m,
3,9x10-3s; c) 19,53m; 3,9x10-3s.
56. Sea la ecuación de una onda 𝑦 = 3𝑐𝑜𝑠2𝜋(10𝑡 − 0,05𝑥), las distancias en cm y los tiempos en segundos.
Calcule a) la frecuencia de esta onda, b) la longitud de onda y c) la rapidez de propagación. Sol.: a) 10 Hz, b)
20 cm, c) 200 cm/s
57. La ecuación de una onda transversal que se propaga en una cuerda es: 𝑦 = 4𝑠𝑒𝑛2𝜋 (
𝑡
0,1
−
𝑥
20
) [𝑐𝑚] (Las distancias
en cm y tiempos en segundos). Hallar la amplitud, el periodo, la frecuencia, la longitud de onda y la rapidez de
propagación. Sol.: 4 cm, 0.1 s, 10 Hz, 20 cm, 200 cm/s
58. Escribir la ecuación de una onda que avanza en el sentido positivo de las x y que tiene por amplitud 3 cm, por
frecuencia 10 Hz y una rapidez de 5 m/s.
Sol.: 𝒚 = 𝟑 𝒔𝒆𝒏 𝟐𝝅(𝟏𝟎𝒕 − 𝟐𝒙)[𝒄𝒎]
59. En una cuerda, una onda de amplitud 3 cm, de periodo 𝜋 segundos y longitud de onda 2𝜋 cm avanza hacia la
izquierda. ¿Cuál es la rapidez de propagación de las ondas? ¿Cuál es la ecuación de la onda? Sol.: 2 cm/s;
𝒚 = 𝟑𝒔𝒆𝒏(𝟐𝒕 + 𝒙)
SONIDO.
60. Calcular la rapidez del sonido en el aire a 28ºC. Sol.: 347,8 m/s
9
61.
Un trueno se oye 6 segundos después de haberse observado el relámpago, calcule la distancia a que cayó el
rayo, temperatura ambiente 22ºC. Sol.: 2065,2 m
62. Una explosión ocurre a una distancia de 6 km de una persona. ¿Qué tiempo transcurre después de la explosión
antes de que la persona la pueda escuchar? Suponga que la temperatura es de 14°C. sol.: 17,6 s
63. Un diapasón vibra en el aire a razón de 284 Hz. Calcule la longitud de onda del tono emitido a 25°C. sol.: 1,22
m
64. Un automóvil se acerca con una rapidez de 90 km/h hacia un observador en reposo, el conductor presiona la
bocina, la cual emite un sonido de 280 Hz. ¿Cuál es la frecuencia percibida por el observador? Rapidez del
sonido 340 m/s. Sol.: 302,22 Hz
65. La sirena de un bus tiene una frecuencia de 550 Hz y se acerca a una terminal terrestre con una rapidez de
108 km/h, donde está un observador estacionario. ¿cuál es la frecuencia del sonido que percibe el observador
al acercarse el bus? Rapidez del sonido 340 m/s. Sol.: 603,22 Hz
66. Un foco emisor estacionario emite una frecuencia de 500 Hz y un observador se acerca hacia él con una
rapidez de 10 m/s. a) ¿Cuál es la frecuencia percibida por el observador?; b) ¿Cuál es la frecuencia cuando el
observador se aleja del foco? Rapidez del sonido 340 m/s. Sol.: a) 514,71 Hz; b) 485,29 Hz
67. Un coche de carrera viaja a 108 km/h por una vía recta y su corneta emite un sonido de 500 Hz. Usted está
parado a la orilla de la vía. a) ¿Cuál es la frecuencia percibida, si el coche se aproxima hacia usted? b) ¿Cuál es
la frecuencia del sonido escuchado si el coche se aleja de usted? Rapidez del sonido 340 m/s. Sol.: a)
548,39 Hz; b) 459,46 Hz
68. Un diapasón de 400 Hz de frecuencia se aleja de un observador y se acerca a una pared con una rapidez de 2
m/s. Calcule la frecuencia aparente a) de las ondas sonoras que llegan directamente al observador, b) de las
ondas sonoras que al observador después de reflejarse en la pared, c) ¿cuántas pulsaciones por segundo se
producen? Se supone que la rapidez del sonido en el aire es de 335 m/s. Sol.: a) 396 Hz, b) 402 Hz, c) 6
Hz.
69. Un automóvil se aproxima a una rapidez de 30 m/s hacia la sirena de una fábrica que tiene una frecuencia de
500 Hz. Suponiendo que la rapidez del sonido en el aire es de 340 m/s, hallar la frecuencia que
aparentemente oye el conductor. Sol.: 544 Hz
70. El silbido de una locomotora a 90 km/h, tiene una frecuencia de 2 000 Hz. Si la rapidez del sonido en el aire
es de 340 m/s, calcule la frecuencia del silbido oída por una persona antes de que la locomotora pase por
delante de ella y después de haber pasado. Sol.: 2160 Hz; 1860 Hz.
10