segundo parcial dinamica 13-02
Anuncio

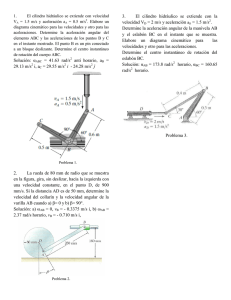
SEGUNDO PARCIAL MECANICA II GRUPO 2. FECHA 13-02-2012 PROFESOR: JUAN CARLOS JIMÉNEZ V. NOTA: ____________ NOMBRE _______________________________________________________ CÓDIGO_________________________ La grandeza de un ideal no es alcanzarlo, sino luchar por él, alcanzarlo es sólo una recompensa. 1. (4 enunciados x 3 puntos/enunciado = 12 puntos) Diga si los siguientes enunciados son verdaderos o falsos y justifique su respuesta. a. Para el punto A del problema 3, se cumple que su aceleración es cero porque el disco tiene velocidad ω constante. b. Para el problema 3, en el elemento AB, cuando β = 0º y cuando β = 90º el centro instantáneo de rotación es el mismo, porque se trata del mismo cuerpo. c. Si dos engranajes de radios r1 y r2 giran acoplados y uno de ellos tiene aceleración angular α constante, el otro tiene el mismo valor de aceleración angular (en magnitud), pero en sentido contrario. d. Si una partícula se desplaza con relación a un marco de referencia en rotación, entonces su aceleración de Coriollis es necesariamente diferente de cero. Resuelva los siguientes ejercicios teniendo en cuenta (se tendrán en cuenta en la calificación): Elaborar diagrama de cada situación que analice. Señale o marque sus respuestas. Emplee las unidades correspondientes. Los valores que se manejen en la resolución de problemas deben salir del enunciado del problema o ser el resultado de la aplicación de una formula. 2. (19 puntos) El cilindro hidráulico se extiende con velocidad VA = 1.5 m/s y aceleración aA = 0.5 m/s2. Elabore un diagrama cinemático para las velocidades y otro para las aceleraciones. Determine la aceleración angular del elemento ABC y las aceleraciones de los puntos B y C en el instante mostrado. El punto B es un pin conectado a un bloque deslizante. con una velocidad constante, en el punto D, de 900 mm/s. Si la distancia AD es de 50 mm, determine la velocidad del collarín y la velocidad angular de la varilla AB cuando a) β= 0 y b) β= 90°. Problema 3. Formulas: 𝑣⃗ = 𝜔 ⃗⃗ × 𝑟⃗ = 𝑟𝜔 𝑣𝐵 = ⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗ 𝑣𝐴 + 𝑣 ⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝐵/𝐴 𝑎⃗ = ⃗⃗⃗⃗ 𝑎𝑡 + ⃗⃗⃗⃗⃗ 𝑎𝑛 = 𝛼⃗ × 𝑟⃗ + 𝜔 ⃗⃗ × (𝜔 ⃗⃗ × 𝑟⃗ ) = 𝛼𝑟 − 𝜔2 𝑟 𝑎𝐵 = 𝑎𝐴 + 𝑎𝐵/𝐴 = 𝑎𝐴 + (𝑎𝐵/𝐴 )𝑡 + (𝑎𝐵/𝐴 )𝑛 Problema 2. 3. (19 puntos) La rueda de 80 mm de radio que se muestra en la figura, gira, sin deslizar, hacia la izquierda 𝑎𝑃 = 𝛺̇ × 𝑟 + 𝛺 × (𝛺 × 𝑟) + 2𝛺 × (𝑟̇ )𝑂𝑥𝑦 + (𝑟̈ )𝑂𝑥𝑦 𝑎𝑐𝑜𝑟 = 2𝛺 × (𝑟̇ )𝑂𝑥𝑦 ¡ÉXITOS!