1.- Un individuo de 80 kg se encuentra en el extremo de una tabla

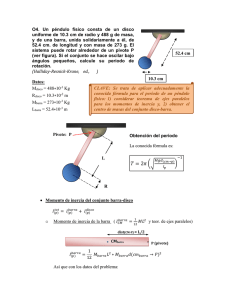
SEGUNDO EXAMEN PARCIAL FÍSICA I
MODELO 1
1 . - Un individuo de 80 kg se encuentra en el extremo de una tabla de 20 kg
de masa y 1 0 m de longitud que flota en reposo sobre la superficie de agua de un
estanque. Si el hombre se desplaza al otro extremo, ¿qué distancia recorre la tabla?
Considera despreciable el rozamiento con el agua.
a) 8 m
b) 4 m
c) 9 m
d) 5 m
a) Puesto que no hay rozamiento, todas las fuerzas que actúan (pesos y normales)
son verticales, y no hay fuerzas horizontales. Así, al no haber fuerzas horizontales la
aceleración del centro de masas en esta dirección es nula, y la velocidad del centro de
masas permanece constante. Puesto que inicialmente es nula, debe seguir siéndolo, y si no
hay velocidad del centro de masa, éste no puede desplazarse. Por tanto, el centro de masas
no se desplaza.
∆xCM=0
Como el centro de masas no puede
moverse, cuando el individuo se desplace
hacia la derecha, la tabla reacciona y se
desplaza en sentido contrario de modo que el
centro de masas permanezca en la misma
posición. Cuando el hombre llega al extremo
derecho tendremos lo que aparece en la
figura. Puesto que la posición del centro de
masas no varía podemos escribir:
m x + m2x2 m1x'1 +m2x'2
=
xCM=x’CM ⇒ 1 1
m1 + m2
m1 + m2
m1x1+m2x2=m1x’1+m2x’2
80x1+20x2=80x’1+20x’2 ⇒ 80x1+20(x1+5)=80 · 10+20 · 5 ⇒ 80x1+20x1+100=800+100
100x1=800 ⇒ x1=8 m
Este dato coincide con el desplazamiento de la tabla.
Respuesta correcta: a)
2. - Un cuerpo A de masa 20 kg se mueve con velocidad de 20 m/s hacia otro
cuerpo B de masa 5 kg que se encuentra inicialmente en reposo. Los cuerpos chocan y
rebotan. Calcular las velocidades de cada cuerpo después de la colisión. Suponer que
no se pierde energía en el choque.
a) v’ A=0 m/s; v’ B=20 m/s
b) v’ A=5 m/s; v’ B=20 m/s
c) v’ A=0; v’ B=20 m/s
d) v’ A=1 2 m/s; v’ B=32 m/s
Se trata de un choque completamente elástico, ya que nos dicen que en el choque no
se pierde energía. Tomamos como eje X la dirección del movimiento (problema escalar) y así
tendremos que se conserva la cantidad de movimiento:
pantes=pdespués ⇒ mAvA+mBvB=mAv’A+mBv’B ⇒ 20 · 20=20v’A+5v’B
Además, como el choque es elástico el coeficiente de restitución vale la unidad:
v' −v'
v' −v'
e = B A ⇒1= B A
vA − vB
20
Y tenemos un sistema de dos ecuaciones y dos incógnitas:
20 · 20=20v’A+5v’B
v' −v'
1= B A
20
De la segunda ecuación:
v' −v'
1 = B A ⇒ v’B=20+v’A
20
Y sustituyendo en la primera:
20 · 20=20v’A+5v’B⇒ 400=20v’A+5(20+v’A) ⇒ 400=20v’A+100+5v’A ⇒ v’A=12 m/s
Y por tanto la otra:
v’B=20+v’A=20+12=32 m/s
Respuesta correcta: d)
3. - Se aplican tres fuerzas a una rueda con radio
0, 350 m, como se indica en la figura. Una fuerza es
perpendicular al borde, otra es tangente a éste y la otra
forma un ángulo de 40º con el radio. ¿Cuál es el momento
neto sobre la rueda debida a estas tres fuerzas para un
eje perpendicular a la rueda y que pasa por su centro?
a) 1 2, 25 Nm
b) 6, 26 Nm
c) - 0, 31 0 Nm
d) 6, 3 Nm
El momento será la suma de los momentos de las tres fuerzas. Como dicho vector
está en el eje Z (perpendicular al plano de la hoja) calculamos solamente su módulo:
M=M1+M2+M3=-14,6sen40º · 0,35+8,50 · 0,35=-0,310 Nm
Respuesta correcta: c)
a)
b)
c)
d)
4. - Un barril de 1 00 kg con un radio de 50 cm tiene
enrolladas dos cuerdas como se muestra en la figura. El barril se
deja caer desde el reposo, haciendo que las cuerdas se desenrollen
y que el barril caiga girando hacia el suelo. ¿Cuál es la tensión en
cada cuerda? Suponga que la masa del barril está uniformemente
distribuida y que el barril gira como un cilindro sólido, de momento
1
mR 2 .
de inercia ICM =
2
326, 67 N
980 N
490 N
1 63, 33 N
cilindro rueda sin deslizar, de modo que:
Hacemos el diagrama de sólido libre del
barril y tendremos lo que aparece en la figura.
Tomamos como eje Y el vertical y positivo
hacia abajo, y aplicamos la segunda ley de
Newton (traslación y rotación):
ΣFY=m(aCM)Y ⇒ mg-2T=maCM
1
4T
ΣMCM=ICMα ⇒ 2TR = mR2α ⇒ α =
2
mR
Tendremos en cuenta ahora que el
aO=aCM=αR
Así, la primera ecuación nos queda:
mg-2T=maCM ⇒ mg-2T=mαR
Y sustituimos la expresión de la aceleración angular en esta ecuación:
mg 100 ⋅ 9,8
4T
R ⇒ mg − 2T = 4T ⇒ T =
=
= 163,33 N
mg-2T=mαR ⇒ mg − 2T = m
mR
6
6
Respuesta correcta: d)
5. - Un aro de 2, 20 kg y de 1 , 20 m de diámetro rueda hacia la derecha sin
deslizar sobre un piso horizontal a 3 rad/s constantes. Calcula el vector velocidad del
punto más alto del aro.
a) 1 , 80 m/s hacia la derecha
b) 0
c) 7, 20 m/s hacia la derecha
d) 3, 60 m/s hacia la derecha
El diámetro del aro es de 1,20 m, de modo que el radio
es la mitad, es decir, 0,60 m. Puesto que el aro rueda sin
deslizar tendremos en cuenta que:
vCM=ωr=3 · 0,60=1,80 m/s
Puesto que el disco va hacia la derecha tendremos que
vectorialmente:
vCM=1,80i
Así, la velocidad del punto más alto del aro, que hemos
llamado punto P será:
i
j
k
0
− 3 = 1,80i + 1,80i = 3,60i
vP = vCM + ω × CMP = 1,80i + 0
0 0,60 0
Respuesta correcta: d)
6. - Un niño de masa M está balanceándose en un columpio de longitud L con un
ángulo máximo de θ. Un hombre con una masa 4M está balanceándose en un columpio
semejante de longitud L con un ángulo máximo de 2θ. Cada columpio puede tratarse
como un péndulo simple experimentando un movimiento armónico simple. Si el período
para el movimiento del niño es T, entonces el período del movimiento del hombre es:
a) T
b) 2T
T
c)
2
T
d)
4
Puesto que se trata de un péndulo simple, para el niño, cuyo período es T,
tendremos:
T = 2π
L
g
Y para el hombre, el período será T’:
T'= 2π
L
=T
g
Vemos que como el período no depende ni de la masa ni de la amplitud, ambos
períodos son iguales.
Respuesta correcta: a)
7. - Un resorte vertical con una constante elástica de 2 N/m tiene una masa
de 0, 3 kg sujeta a éste y la masa se mueve en un medio con una constante de
amortiguamiento de 0, 0250 kg/s. Se libera la masa a partir del reposo en una posición
de 5 cm a partir de la posición de equilibrio. ¿Cuánto tiempo pasa hasta que la
amplitud disminuye a 1 , 5 cm?
a) 1 6, 22 s
b) 8, 1 1 s
c) 28, 89 s
d) 1 4, 48 s
Veamos en primer lugar el tipo de amortiguamiento, para lo que comparamos el
parámetro de amortiguamiento con la frecuencia natural del oscilador. El parámetro de
amortiguamiento es:
0,0250
γ
β=
=
= 0,0417 s −1
2m
2 ⋅ 0,3
Y la frecuencia natural:
ω0 =
k
=
m
2
= 2,582 s −1
0,3
Puesto que β<ω0 el movimiento es subamortiguado. Tendremos que la ecuación del
movimiento es:
x=A0e-βtsen(ω’t+ϕ)=Asen(ω’t+ϕ)
siendo A una amplitud que no es constante, sino que decrece en el tiempo en la forma:
A=A0e-βt ⇒ 1,5=5e-0,0417t ⇒ 0,3=e-0,0417t ⇒ ln0,3=-0,0417t ⇒ t=28,89 s
Respuesta correcta: c)
8. - Para un sólido rígido: a) demostrar el teorema de Steiner; b) definir radio
de giro; c) definir ejes principales de inercia.
a) Existe una relación entre los momentos de
inercia de un sólido con respecto a dos ejes paralelos, uno
de los cuales pasa por el centro de masas: es el denominado
teorema de Steiner.
Para demostrarlo, consideremos un cuerpo
cualquiera, y tomemos finas rodajas del mismo. Con una
rodaja basta, ya que el análisis sería idéntico para todas las
rodajas. Tomamos el plano XY en el plano de la rodaja y el
eje Z perpendicular a la misma, es decir, coincidente con
los dos ejes paralelos. Así, todos los puntos de la rodaja
tienen la misma coordenada z. El centro de masas lo hacemos coincidir con el origen de
coordenadas, y el punto P (por el que pasa el eje paralelo al que pasa por el centro de
masas), está situado a una distancia d del anterior. Tomemos una partícula i del sólido,
situada a una distancia ri del origen de coordenadas. Este vector será:
ri=xii+yij+zk
El punto P se encuentra a una distancia d del centro de masa, y podemos poner:
d=ai+bj+zk
Hacemos un gráfico donde veamos esta situación
desde arriba, con lo que tenemos lo que aparece en la
figura. El momento de inercia respecto de un eje que
pasa por el centro de masas será, sumando para todas
las partículas de la rodaja:
(
N
N
ICM = ∑ miri2 = ∑ mi xi2 + yi2 + z2
i =1
i =1
)
Hemos tenido en cuenta la definición de módulo de un vector:
será:
ri=xii+yij+zk ⇒ ri = xi2 + yi2 + z2 ⇒ ri2 = xi2 + yi2 + z2
Y del mismo modo, el momento de inercia respecto del eje que pasa por el punto P
N
N
i=1
i=1
[
]
IP = ∑ mir'i2 = ∑ mi (xi − a )2 + (yi − b)2 + z2 =
N
N
i =1
N
i =1
N
N
N
N
N
N
i =1
i =1
N
= ∑ mixi2 + ∑ mia2 − 2 ∑ mixia + ∑ mi yi2 + ∑ mib2 − 2 ∑ mi yib + ∑ miz2 =
N
(
= ∑ mi xi2 +
i =1
i =1
N
i =1
i =1
N
N
= ∑ mixi2 + ∑ mi yi2 + ∑ miz2 + ∑ mia2 + ∑ mib2
i=1
i=1
i=1
i=1
i=1
N
N
N
yi2 + z2 + ∑ mi a2 + b2 − 2a ∑ mixi − 2b ∑ mi yi
i =1
i =1
i =1
)
(
)
N
− 2 ∑ mixia − 2 ∑ mi yib =
i=1
N
(
i=1
)
N
(
= ∑ mi xi2 + yi2 + z2 + ∑ mi a2 + b2
i =1
i =1
)
Tenemos en cuenta que xi e yi son las coordenadas de la partícula i-ésima respecto
del centro de masas, y ya habíamos obtenido en el tema 4, que en un sistema de referencia
centro de masas:
N
∑ mixi = 0
i=1
N
∑ mi yi = 0
i=1
Así, tendremos:
(
)
(
)
N
N
IP = ∑ mi xi2 + yi2 + z2 + ∑ mi a2 + b2 = ICM + md2
i =1
i =1
Esta última ecuación es el teorema de Steiner, que dice que el momento de inercia
de un cuerpo respecto a un eje cualquiera es igual al momento de inercia del mismo cuerpo
respecto a un eje paralelo al anterior que pase por el centro de masas, más el producto de
la masa del cuerpo por el cuadrado de la distancia entre ambos ejes. Esta ecuación nos
muestra que de todos los ejes paralelos a una dirección dada, el que pasa por el centro de
masas del cuerpo es al que le corresponde el momento de inercia más pequeño.
b) El momento de inercia presenta distintas expresiones en función de la forma
(distribución de masa) del cuerpo. No obstante, siempre es posible expresar el momento de
inercia de cualquier cuerpo como:
I=mk2
siendo k el denominado radio de giro del sólido rígido
correspondiente respecto a dicho eje. El radio de giro
representa por tanto, la distancia a la que habría que
concentrar toda la masa del cuerpo de forma que el
momento de inercia respecto del giro se mantuviera
invariable. Se tiene entonces que:
I=mk2 ⇒ k =
I
m
c) En un sólido rígido, si el eje de rotación es un eje de simetría el momento angular
L y la velocidad angular ω son paralelos. Sin embargo, si el eje de rotación no es un eje de
simetría, las componentes en dirección perpendicular al eje de rotación no se compensan y
el momento angular L y la velocidad angular ω no son paralelos. No obstante, siempre es
posible demostrar que en todo cuerpo existen al menos tres direcciones mutuamente
perpendiculares para las cuales el momento angular es paralelo al eje de rotación. Estos
ejes se conocen como ejes principales de inercia, y los momentos de inercia
correspondientes como momentos principales de inercia. Si el cuerpo tiene algún eje de
simetría, los ejes principales de inercia coinciden con los ejes de simetría.