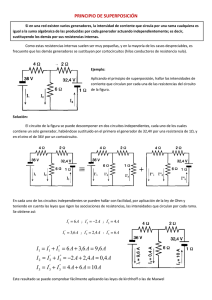
Corriente continua.
Anuncio

EMBA Apuntes EB- Corriente continua Corriente continua. 1. Introducción. Todas las herramientas utilizadas para el manejo del sonido están basadas en sistemas electrónicos. La mayoría de las especificaciones que dan los fabricantes de los equipos que hemos de utilizar para nuestro trabajo, son especificaciones de carácter eléctrico. Tomar decisiones sobre componentes de un sistema implica interpretar especificaciones como las que siguen: El amplificador CROWN Macro-tech 600 presenta una impedancia de entrada de 20 kilo ohm (kΩ) balanceada y 10 kΩ desbalanceada. Una impedancia de salida de menos de 10 mili ohm (mΩ). Su sensibilidad es de 1,4 volt (V) para una potencia de salida de 235 watt (W) a 1 kHz sobre 8 Ω de carga con 0,1 % de distorsión armónica total (THD). Esto para ambos canales funcionando simultáneamente. Con alimentación de 120 volt de corriente alterna (VAC) consume en reposo menos de 100 W. Con un tono continuo de 1 kHz senoidal, sobre 4Ω en puente y entregando 540 W consume 28 amperes (A). Por otra parte la norma IEC 1938 establece que la alimentación Phantom deberá suministrar como máximo 10 mili amperes (mA) con 48 ± 4 V y con resistencias de 6800 Ω en serie con las líneas balanceadas. Los fenómenos eléctricos que estudiaremos guardan cierta analogía con otros fenómenos con los cuales estamos más familiarizados y, siempre que se pueda utilizaremos esas analogías. Todas las actividades técnicas tienen como fin realizar un trabajo y para ello es necesario convertir cierta cantidad de energía con la necesaria potencia. Los conceptos de trabajo, energía y potencia tienen gran importancia para que podamos entender este texto y es necesario que el estudiante no pase por alto dudas al respecto. Podrá encontrar una definición elemental en el texto relativo al movimiento armónico simple (MAS) utilizado en PTA. Es importante encontrar la forma de energía más apropiada para realizar el trabajo que nos proponemos. La energía eléctrica resulta muy apropiada para mucha aplicaciones por ser la más fácil de transportar, la más fácil de convertir en otra y la más fácil de controlar mediante las técnicas de la ingeniería electrónica. Permite además grandes velocidades de respuesta, imprescindibles para el manejo del sonido. Puede construirse un amplificador hidráulico, con pistones y caños llenos de aceite impulsado por una bomba. De hecho el sistema de servofrenos de un automóvil es un amplificador que permite con una pequeña fuerza ejercida en el pedal (señal de entrada) realizar una gran fuerza de frenado en las ruedas (señal de salida). Pero resultaría muy grande, muy pesado, muy sucio, muy caro y de muy pobre respuesta de frecuencia (muy lento). Las primeras máquinas de grabar sonido (fonógrafo) convertían las variaciones de presión del aire, provocadas por la onda sonora, directamente en movimiento de una aguja que grababa un surco sinuoso sobre un cilindro de cera. El mecanismo comprendía Ing. Aldo Lugli Tancredi 1 EMBA Apuntes EB- Corriente continua una bocina, una membrana y una palanca que impulsaba la aguja, al que puede considerarse una forma particular de amplificador. En el oído hay un mecanismo que puede considerarse una forma particular de amplificador. Es el formado por la cadena de huesos que conectan el tímpano con la membrana basilar (martillo, yunque y estribo). Estos sistemas son o bien de funcionamiento limitado o muy complicados para ser construidos en serie a un precio razonable y de muy difícil control de sus características (controles de tono y ganancia por ejemplo). El conocimiento de los fenómenos eléctricos se remonta a los antiguos griegos, que ya en el año 600 AC atraían cuerpos livianos con una varilla de ámbar frotada con lana. La palabra griega elektron significa ámbar y de ella derivan todas las palabras relacionadas con electricidad. Posteriormente se experimentó con otros materiales, por ejemplo vidrio frotado con seda o ebonita frotada con piel, los que también atraían cuerpos livianos, como por ejemplo pequeños trozos de papel. Cuando se produce este fenómeno de atracción se dice que la varilla está cargada de electricidad, o que presenta carga eléctrica. Experimentado con pequeños objetos se llega a la conclusión que existen dos tipos de carga eléctrica. La que se produce con la ebonita frotada con piel, llamada negativa, y la que se obtiene frotando vidrio con seda, llamada positiva. La denominación de positiva y negativa, que es arbitraria, no es calificativa sino que simplemente distingue un tipo de carga de otra. Si se enfrentan cuerpos cargados con cargas iguales se producirá una fuerza de repulsión, mientras que si los cuerpos tienen cargas diferentes se atraerán. La energía eléctrica se transporta mediante el desplazamiento de cargas eléctricas, las que realizan el trabajo para el cual fue diseñado el dispositivo en el que son aplicadas. Como ejemplo de esos dispositivos tenemos a la estufa eléctrica, que convierte energía eléctrica en calor, el parlante que la convierte en ondas sonoras, el motor eléctrico, la lámpara de iluminación. 2. Carga eléctrica. Todas las técnicas relacionadas con la electricidad se basan en el adecuado manejo de las cargas eléctricas. La carga eléctrica es una propiedad de la materia. Radica en las partículas que forman los átomos y se manifiesta mediante fuerzas ejercidas entre cuerpos que presentan carga eléctrica, y esta fuerza es la que, precisamente, les permite realizar un trabajo. El modelo atómico en uso actualmente consiste básicamente en un núcleo alrededor del cual giran partículas llamadas electrones. El núcleo está formado por partículas llamadas protones y neutrones. Los electrones tienen carga eléctrica negativa. Los protones tienen carga eléctrica positiva y los neutrones no manifiestan carga eléctrica. 2 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua electrón núcleo Figura 2.1 La masa del electrón es muy pequeña comparada con la del protón. Las diferencias que tienen los elementos naturales entre si se deben a la cantidad de protones, electrones y neutrones que componen sus átomos. Mientras que el átomo de hidrógeno (H) tiene un electrón y un protón, el del cobre (Cu) tiene 29 electrones y 29 protones. Todos los átomos en estado natural presentan igual cantidad de electrones que de protones. La cantidad de carga eléctrica de un electrón es igual a la del protón, si unimos un protón y un electrón los efectos de las cargas individuales se compensarán y no se manifestará carga eléctrica sobre cualquier cuerpo externo. Por ello los átomos en estado natural y la materia que ellos componen no presentan carga eléctrica. Si a un trozo de materia le extraemos electrones, entonces en ese cuerpo se producirá un desequilibrio y presentará carga eléctrica positiva. Los electrones extraídos desequilibrarán también al cuerpo en donde fueron depositados haciendo que este presente carga eléctrica negativa. Cuando frotamos una regla de plástico con la bufanda la regla adquiere cierta cantidad de carga eléctrica y la bufanda adquiere la misma cantidad de carga eléctrica pero de signo contrario al de la regla. Solo se pueden mover de un cuerpo a otro, electrones. Los protones son inamovibles sin producir cambios sustanciales en la estructura de los cuerpos. El cuerpo que pierde electrones resulta con carga positiva, el que los gana resulta con carga negativa. Si consideramos a ambos cuerpos, el total de carga eléctrica será cero pues hay tanta carga negativa como positiva y se neutralizan. La mínima cantidad de carga eléctrica es la del electrón (igual a la del protón) y no puede dividirse. Para cargar eléctricamente a un cuerpo es necesario quitarle o agregarle electrones. A mayor cantidad de electrones, mayor cantidad de carga eléctrica. Cuando se carga un cuerpo, simultáneamente se carga otro con igual cantidad de carga de signo contrario. Ing. Aldo Lugli Tancredi 3 EMBA Apuntes EB- Corriente continua Carga negativa Exceso de electrones Carga positiva Defecto de electrones Figura 2.2 La figura 2.2 muestra dos cuerpos cargados, uno negativo y el otro positivo aislados, es decir, dispuestos de manera tal que las cargas en exceso de uno no pueden desplazarse hacia el otro. Los cuerpos con carga eléctrica suponen un desequilibrio. La tendencia natural es el equilibrio eléctrico. Si habiendo cuerpos con cargas eléctricas diferentes, permitimos el movimiento de las cargas de uno al otro se reestablecerá el equilibrio mediante el desplazamiento de los electrones desde el cuerpo que presenta carga negativa hacia el que presenta carga positiva. Un ejemplo natural es el rayo. 2.1 Campo eléctrico. Un cuerpo con carga eléctrica ejercerá fuerzas de atracción o repulsión sobre otros cuerpos cargados. Esa fuerza sobre otros cuerpos cargados es la manifestación de la carga eléctrica. Llamamos campo eléctrico a toda la zona del espacio que rodea a un cuerpo cargado eléctricamente en la que se manifiestan los efectos de la carga eléctrica. Dados dos cuerpos con carga eléctrica la fuerza de atracción o repulsión que se desarrollará entre ellos está dada por la ley de Coulomb. G Q ⋅Q F =k⋅ 1 2 2 d 2.1.1 En la que Q1 y Q2 son las cantidades de carga de cada cuerpo, d es la distancia entre ellos y k es una constante que depende del medio en el que se desarrolla la experiencia y del sistema de unidades utilizado. Esta ley es válida si la distancia es mucho mayor que el diámetro de los cuerpos cargados, supuestos esféricos. Nótese la similitud con la ley de Newton de la atracción gravitatoria. Básicamente mientras que en la ley de Coulomb figuran las cantidades de carga eléctrica de los cuerpos en la Newton aparecen las masas de los cuerpos. 4 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua Una gran diferencia entre el campo gravitatorio y el eléctrico es que mientras las masas solo se atraen las cargas eléctricas pueden atraerse o repelerse. Si suponemos cuerpos esféricos, en ambos casos las fuerzas son de dirección radial a los mismos. La cantidad de carga eléctrica se mide en culombio o coulomb y se abrevia C. Un culombio equivale a aproximadamente 6.300.000.000.000.000.000 de electrones, que escrito en forma científica resulta: 1C ≈ 6,3 × 1018 e 2.1.2 Una manera de estudiar el campo eléctrico de un cuerpo cargado es observar que efectos tiene ese campo sobre una carga conocida. Se suele tomar como carga de pruebas un cuerpo con carga positiva. Figura 2.3 La figura 2.3 representa el campo creado por un cuerpo esférico con carga negativa. Las flechas son los vectores que representan a las fuerzas que ejercerá el cuerpo cargado sobre la carga de prueba, y como esta es positiva, entonces el cuerpo negativo la atraerá. Las distintas flechas corresponden a distintas posiciones del cuerpo de prueba, para cada posición habrá una flecha que represente la fuerza en ese punto. Figura 2.4 Si nos alejamos la fuerza disminuirá en proporción al cuadrado de la distancia. Ing. Aldo Lugli Tancredi 5 EMBA Apuntes EB- Corriente continua De esta manera resultará que a medida que nos alejamos la fuerza decrecerá pero nunca será nula (deberíamos alejarnos hasta el infinito) puede decirse entonces que el campo eléctrico, al menos teóricamente, será infinito. En realidad, como no hay un solo cuerpo cargado, a medida que nos alejamos de uno nos acercaremos a otro con lo que los efectos del primero quedarán enmascarados por los del segundo. Obsérvese que las fuerzas ejercidas por un cuerpo con carga eléctrica negativa son similares a las que ejerce la tierra sobre cualquier cuerpo a su alcance (esto se debe a que se toma como carga de prueba una positiva). Las fuerzas son radiales y hacia adentro. La figura 2.4 muestra el campo de un cuerpo con carga positiva, y como cargas del mismo signo se repelen, entonces las fuerzas son centrífugas (hacia fuera). Recuérdese que siempre utilizamos como carga de prueba una positiva. En el vacío y para el sistema de unidades MKS (metro, kilogramo, segundo), la constante k, de la ecuación 2.1.1 resulta: k ≈ 9 × 109 2.2 N ⋅ m2 ⋅ C −2 Potencial eléctrico. La idea de potencial eléctrico es de fundamental importancia y para comprenderla mejor analizaremos un concepto análogo, el del potencial gravitatorio, con el que estamos muy familiarizados. Si acumulamos piedras o agua a cierta altura y las dejamos caer, esas piedras o el agua podrán realizar un trabajo. A lo largo del proceso habrá una sucesión de trabajos que constituyen transformaciones de la energía. Veámoslo gráficamente. A Figura 2.5 En la figura 2.5 alguien comienza a hacer subir un objeto A, supongamos una gran piedra, por una cuesta. Debido a que se encuentra en movimiento podemos asegurar que el trabajo que está haciendo la persona que empuja se convierte en energía cinética y la piedra se desplaza. 6 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua A Figura 2.6 A medida que aumente la altura, y gracias a la energía cinética aportada por la persona que empuja, la energía potencial de la piedra aumentará. A Figura 2.7 En las figura 2.7 se habrá llegado a la altura máxima del recorrido. Detenido el movimiento la piedra habrá alcanzado su máxima energía potencial. En el caso del campo gravitatorio la energía potencial adquirida dependerá del incremento de altura experimentado y de la masa del cuerpo. Si ahora dejamos caer la piedra, la energía potencial se convertirá en cinética y al final del recorrido la piedra podrá hacer un trabajo, como por ejemplo, dar un golpe a otro objeto. Es importante que tengamos en cuenta que al analizar estas cuestiones físicas no importa la utilidad o inutilidad del trabajo. Es trabajo desde el punto de vista físico y no económico. Este ejemplo podríamos hacerlo mucho más práctico si en lugar de piedras lo que acumula energía potencial es agua y en lugar de subirla con baldes la juntamos en una laguna a la que llegan ríos que vienen de lugares más altos. Luego la dejamos caer y hacemos que mueva unas paletas que hacen girar un eje. Ing. Aldo Lugli Tancredi 7 EMBA Apuntes EB- Corriente continua Ese eje a su vez mueve unas poleas que accionan un generador eléctrico (como el de la bicicleta) y con la electricidad alimentamos unas lámparas y así obtenemos iluminación gratuita. ¿Habremos generado energía de la nada? El principio de conservación de la energía establece que eso no es posible. La energía no se crea ni se destruye, se transforma. En realidad el agua que viene de tierras arriba y que acumulamos en una laguna, llegó a las tierras altas gracias a la lluvia, y llovió gracias a la acumulación de vapor de agua en la atmósfera. Esto último es posible gracias a la evaporación del agua que, es debida a la acción del sol, fuente original de la mayoría de la energía que de una u otra manera utilizamos en el planeta. Cuando hablamos de altura no decimos nada si no establecemos respecto de qué nivel la medimos. En otras palabras debemos establecer un cero o referencia para medir las alturas. Tomemos una referencia válida para todos nosotros, es decir que podamos acceder a ella y de esa manera poder repetir las experiencias. Tomemos por ejemplo la base de la pirámide de mayo. Altura será entonces la distancia medida en dirección vertical entre la referencia (la base de la pirámide de mayo, en nuestro ejemplo) y el punto en cuestión. A propósito, se sugiere al estudiante averiguar cuál es el cero de alturas de la ciudad de Buenos Aires. Está cerca de la pirámide de mayo. La energía potencial gravitatoria que adquiere un cuerpo al ser elevado depende de la masa del mismo y del aumento de altura respecto del punto de partida. Si dejamos caer un cuerpo desde cierta altura la energía potencial gravitatoria se irá convirtiendo paulatinamente en energía cinética. Cuanto más distancia recorra mayor será su velocidad y mayor será su energía cinética. A medida que el cuerpo cae y aumenta su energía cinética disminuye su energía potencial. La figura 2.8 nos muestra un ejemplo de aprovechamiento de energía potencial acumulada en un tanque de agua. La altura del agua, más precisamente la altura de la superficie del agua, y la masa del agua acumulada determinan la energía potencial gravitatoria acumulada. Si dejamos caer el agua, esta adquirirá energía cinética y al chocar con las palas de la rueda la hará girar. Cuanto mayor sea la energía cinética del agua, mayor será el trabajo que pueda realizar la rueda. Por lo tanto lo más importante no es la propia altura del agua, es decir su energía potencial, sino la diferencia entre la energía potencial que tiene el agua al comenzar la caída y la energía potencial que le queda al pegar contra la rueda. Cuanto mayor sea esta diferencia, mayor será la energía cinética con que el agua acciona la rueda. 8 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua Depósito de agua Altura del agua Rueda Altura de la rueda Nivel de referencia (cero de alturas) Figura 2.8 Puede decirse que el trabajo realizado por el agua será proporcional a la disminución de energía potencial (o caída de potencial) que sufre el agua desde que comienza a caer y hasta que choca con la rueda. Altura h2 Masa M Fuerza F Altura h1 Figura 2.9 En la figura 2.9 la masa M (agua, piedras o lo que fuere) es movida por la fuerza F que la desplaza desde h1 hasta h2 (alturas medidas desde el nivel de referencia). Al llegar a la altura h2, la masa, habrá aumentado su energía potencial (Ep) en una cantidad ∆Ep cuyo valor será igual al trabajo realizado para llevarla desde h1 hasta h2, es decir: (La letra griega ∆, delta mayúscula, se utiliza en el sentido de “incremento”) ∆Ep = W = F ⋅ (h2 − h1) Ing. Aldo Lugli Tancredi 2.2.1 9 EMBA Apuntes EB- Corriente continua donde W es el trabajo realizado y (h2-h1) la distancia recorrida. Como la fuerza realizada es igual al peso del cuerpo, entonces: W = m ⋅ g ⋅ (h2 − h1) 2.2.2 donde m es la masa del cuerpo y g la aceleración de la gravedad que en el caso de la tierra es aproximadamente 9,81m.s-2 (esto es válido si suponemos que las diferencias de alturas son muy pequeñas respecto del radio de la tierra). Vale decir que para cada altura diferente, el mismo cuerpo tiene energías potenciales diferentes. O sea que podríamos hablar de alturas en metros o de potenciales si utilizamos siempre la misma masa, y eso nos permitiría definir un punto del campo gravitatorio al igual que su altura respecto de alguna referencia. ¿Qué tiene esto que ver con las cargas eléctricas? Bueno, supongamos ahora que a un cuerpo con cierta cantidad de carga eléctrica le acercamos otro, también cargado. Ambos se repelerán o atraerán, dependiendo que sus cargas sean de signo igual o contrario. Tomemos como referencia de distancias al primer cuerpo (parecerá que el que se mueve es el segundo solamente). En cualquier punto del campo eléctrico del primer cuerpo, el segundo cuerpo adquirirá cierta cantidad de energía potencial (esta vez energía potencial eléctrica) pues si lo soltamos se desplazará realizando un trabajo y convirtiendo a la energía potencial eléctrica el energía cinética. Muy parecido con lo que sucede en el campo gravitatorio solo que dependiendo del signo de las cargas el cuerpo se acercará o se alejará del primero. Al ver la ley de Coulomb observamos que su forma es similar a la ley de Newton de la gravedad, a condición de cambiar masa por carga (y las unidades de medida). Es posible entonces pensar en términos de potencial eléctrico así como a diario lo hacemos aquí parados en la tierra. Ese potencial estará dado por el trabajo que hay que realizar para llevar a la unidad de carga eléctrica positiva desde la referencia de distancias hasta dicho punto. Se toma como referencia de distancias a aquella en la que el potencial es cero, es decir donde la fuerza del campo eléctrico es nula, o sea el infinito. Definiremos entonces al potencial en un punto del campo eléctrico como el trabajo que hay que realizar para traer desde el infinito a la unidad de carga eléctrica positiva. Pero como hemos visto al hablar del trabajo realizado por el agua al caer, lo importante no es la altura (o potencial) del agua al iniciar la caída sino la diferencia de alturas entre el inicio y fin del recorrido en el que hace el trabajo (diferencia de potenciales) De igual, manera lo importante en un campo eléctrico, al analizar su capacidad para hacer un trabajo será la diferencia de potencial entre los puntos inicial y final del recorrido. Llamaremos, diferencia de potencial entre dos puntos de un campo eléctrico al trabajo que hay que realizar para llevar a la unidad de carga eléctrica positiva desde uno al otro punto. 10 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua A B Figura 2.10 En la figura 2.10 la diferencia de potencial entre los puntos A y B vendrá dada por la siguiente expresión: VAB = W Q 2.2.3 en la que VAB representa a la diferencia de potencial entre los puntos A y B, W es el trabajo realizado y Q la cantidad de carga transportada desde A hasta B. Véase que el trabajo realizado dividido por la cantidad de carga transportada no es otra cosa que la cantidad de trabajo realizado para transportar a la unidad de carga desde un punto a otro. Si el trabajo se mide en julios y la carga en culombios la diferencia de potencial resultará medida en voltios, que se abrevia V (con mayúscula pues el nombre volt se toma de un apellido). Siempre que halla una diferencia de potencial, se podrán poner cargas eléctricas en movimiento y entonces se podrá realizar un trabajo convirtiendo a la energía eléctrica en otra forma de energía. Como queda dicho, la manifestación del campo eléctrico es la fuerza que este hace sobre un cuerpo cargado. Si según la ley de Coulomb la fuerza en un medio dado depende de las cargas y de la distancia entre ellas entonces se puede adoptar, como medida cuantitativa del campo, la fuerza que este ejerce sobre la unidad de carga positiva en un punto cualquiera del campo. A esta magnitud se la denomina intensidad del campo eléctrico o campo eléctrico y se la representa con la letra E la que por ser una fuerza resultará una cantidad vectorial (se la representará en negrita) Ε= F Q 2.2.4 que se medirá en N/C ó N.C-1 Ing. Aldo Lugli Tancredi 11 EMBA Apuntes EB- Corriente continua Ahora estamos en condiciones de establecer con más precisión una analogía entre el campo eléctrico y el gravitatorio. Observemos la figura 2.10 y llamemos Q a la carga encerrada en el cuerpo que crea el campo representado en ella. Supongamos ahora que en el punto A ubicamos un cuerpo con carga Qp que utilizaremos como carga de prueba. La fuerza entre estos cuerpos será, aplicando la fórmula 2.1.1: F =k⋅ Q ⋅ Qp d2 entonces el vector campo eléctrico en ese punto podrá ser calculado utilizando la ecuación 2.2.4 y resultará: F E= = Qp k⋅ Q ⋅ Qp d2 = k ⋅ Q Qp d2 podemos observar que el vector campo eléctrico producido por un cuerpo cargado depende de la carga de este, de la distancia hasta el cuerpo de prueba y es independiente de la carga del cuerpo de prueba. De igual manera, en el campo gravitatorio, la aceleración producida por el cuerpo que genera el campo depende de la masa de este y de la distancia hasta el cuerpo de prueba. Ambos campos producen fuerzas, y de la ecuación 2.2.4, la producida por el campo eléctrico puede ser calculada de la siguiente manera: F = Qp ⋅ E y si, como sabemos, en el campo gravitatorio F = M ⋅ g podremos establecer una analogía entre masa gravitatoria y carga eléctrica, y entre vector aceleración de la gravedad y vector campo eléctrico. Ejercicios de aplicación y repaso. 2.1 2.2 45,0° Un cuerpo es desplazado 6 m en la misma dirección y sentido que la fuerza aplicada. Si la misma es de 300 N calcular el trabajo realizado. El cuerpo representado en la figura se puede desplazar solo en la dirección A-B y se le aplica una fuerza de 48 N a 45º de esa dirección. Calcular el trabajo realizado si se desplaza 5,5 m. F A B Ejercicio 2.2 2.3 2.4 2.5 2.6 12 Si el trabajo calculado en el ejercicio 2.2 se realizó en 12 s, calcular la potencia desarrollada. Un cuerpo de 25 kg de masa es elevado desde una altura de 3 m a una de 15 m. Calcular la energía adquirida en el recorrido. ¿Cuánto pesa el cuerpo del ejercicio anterior? Un cuerpo se desplaza con movimiento rectilíneo a 25 m/s y 12 s después su velocidad es de 40 m/s. Calcular la aceleración. Ing. Aldo Lugli Tancredi EMBA 2.7 2.8 2.9 2.10 2.11 2.12 Apuntes EB- Corriente continua Un cuerpo se desplaza con movimiento rectilíneo a 60 m/s y 20 s después su velocidad es nula. Calcular la aceleración. Calcular la velocidad inicial del cuerpo del ejercicio anterior en km/h. Un cuerpo de 60 N de peso se mueve con dirección horizontal a 6 m de altura y a una velocidad de 15 m/s. Si recorre 8 m, calcular la energía potencial que tiene al comienzo y al final del recorrido. Graficar tres rectas cuyas pendientes sean 4, -3 y 1 y que pasen por el origen de coordenadas. Graficar una recta de pendiente -3 que pase por el punto (2; -6) Un cuerpo recorre tres tramos rectos a diferentes velocidades. El primero es de 6 m y lo recorre en un minuto, el segundo es de 400 cm y demora 85 s y el tercero, que es de 0,025 km, le insume ¼ de hora. Calcular la velocidad en cada tramo en m/s, la velocidad promedio y la distancia total recorrida. Ing. Aldo Lugli Tancredi 13 EMBA 2.13 Apuntes EB- Corriente continua Conductores y aisladores. Supongamos que disponemos de un cuerpo al que le inyectamos o extraemos electrones. En el primer caso adquirirá carga negativa y en el segundo positiva. En ambos casos diremos que el cuerpo fue cargado. La carga suministrada se dispersará por el cuerpo a diferentes velocidades, dependiendo del material con el que está formado el cuerpo. En algunos materiales la carga se desplazará muy rápidamente, casi instantáneamente. Con otros la carga permanecerá casi sin moverse, no llegará a distribuirse por el cuerpo. A los primeros se les llama conductores y a los segundos aisladores. En un conductor perfecto las cargas se distribuirían instantáneamente y en un aislador perfecto se mantendrían eternamente en el mismo lugar, sin moverse. Ambos extremos son teóricos y solo podremos decir que hay buenos conductores y buenos aisladores. En el primer caso las cargas tienen mucha movilidad mientras que en el segundo la movilidad es poca. Son ejemplo de buenos conductores los metales, las soluciones de sales en agua y los gases ionizados. Son buenos aisladores el vidrio, el agua pura, la goma y la mayoría de los plásticos. 2.4 Capacidad eléctrica. Imaginemos ahora a dos cuerpos conductores cargados con cantidades de carga igual y contraria. Además imaginemos que esos cuerpos están aislados entre si y de cualquier otro cuerpo. Es decir sin caminos posibles para el movimiento de las cargas de cada cuerpo. Figura 2.11 En estas circunstancias se creará un campo eléctrico como lo muestra la figura 2.11. Cualquier carga que se liberara a la acción de este campo sería arrastrada por el efecto combinado del rechazo de uno de ellos y la atracción del otro. Entre estos cuerpos aparecerá una diferencia de potencial. Si aumentamos la cantidad de carga de cada cuerpo, la diferencia de potencial aumentará en la misma proporción. Por esta razón la relación entre la cantidad de carga y la diferencia de potencial será constante, y se denomina capacidad eléctrica. La capacidad eléctrica o capacidad depende de la distancia entre los conductores, su tamaño y el material que los separa. 14 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua C= Q V 2.4.1 en la que C es la capacidad, Q la cantidad de carga de cada conductor y V la diferencia de potencial que se desarrolla entre ellos. La unidad de medida de la capacidad es el faradio o faraday y se representa con F. El faradio es una unidad muy grande para casi todos los fines prácticos y es usual utilizar fracciones tales como el microfaradio (µF), el nanofaradio (nF) o el picofaradio (pF). La capacidad tiene efectos interesantes sobre el comportamiento de los circuitos. Siempre que dos conductores se encuentren aislados, por ejemplo los conductores del cable de una guitarra eléctrica, presentarán capacidad pudiendo por ejemplo modificarnos el timbre del sonido de esa guitarra, como veremos más adelante. Los elementos fabricados para aprovechar el fenómeno de la capacidad se denominan capacitores o condensadores y son utilizados en circuitos de audio para la construcción de filtros entre otras cosas. Otra interesante aplicación del condensador. Como la capacidad de dos láminas planas paralelas depende de la superficie enfrentada de estas, su separación y el material utilizado como aislante, resultará que si hacemos variar la distancia entre las placas, manteniendo el resto constante, variará la capacidad. Si además mantenemos constante la cantidad de carga en las placas la diferencia de potencial entre las placas variará con la distancias entre ellas. Supongamos ahora que una de las placas es una membrana muy fina expuesta adecuadamente a las variaciones de presión del aire. Entonces las variaciones de presión del aire harán variar la distancia entre las placas y producirán variaciones de diferencia de potencial entre las mismas. Dispondremos entonces de un micrófono de condensador. Ing. Aldo Lugli Tancredi 15 EMBA 2.5 Apuntes EB- Corriente continua Generador eléctrico. Volvamos ahora a la figura 2.11 e imaginemos que ambos cuerpos son unidos por un cilindro de material conductor, un alambre de metal por ejemplo ,figura 2.12. Figura 2.12 Este alambre permitirá que las cargas negativas se muevan fácilmente desde donde sobran (cuerpo negativo) y son repelidas hacia donde faltan (cuerpo positivo que las atrae). Este desplazamiento de cargas es lo que se conoce como corriente eléctrica. El nombre hace pensar en el movimiento de cargas como si se tratara de un fluido (un líquido o un gas). En un cuerpo buen conductor los electrones de las capas exteriores de los átomos tienen suficiente energía como para hallarse débilmente atraídos por el núcleo. De esta manera el cuerpo tiene gran cantidad de cargas libres y capaces de trasladarse aplicándosele un campo eléctrico u otra forma de energía externa (luz o calor). Figura 2.13 Un alambre conductor puede imaginarse como un caño lleno de bolitas, como en la figura 2.13. Bastará con que en un extremo del caño introduzcamos una bolita para que en ese mismo momento, en el otro extremo, salga otra bolita. Visto desde afuera parecerá que la bolita que metimos en una punta salió instantáneamente por la otra. En realidad, más que el desplazamiento de cargas en un conductor, el fenómeno es el de una onda. 16 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua De todos modos es como si fuera la corriente de un fluido y el término corriente eléctrica se conserva. No es raro escuchar hablar del “fluido eléctrico” en los informativos cuando hablan de apagones. Sigamos ahora con los cuerpos cargados que unidos con un conductor produjeron una corriente eléctrica. A la unión eléctrica la llamamos conexión. Al circular los electrones desde el cuerpo negativo hacia el positivo irá disminuyendo la cantidad de carga en cada cuerpo. Con ello disminuirá la diferencia de potencial hasta que, cuando hayan pasado la totalidad de las cargas que sobraban en el cuerpo negativo y que faltaban en el positivo, se detendrá la corriente. La corriente eléctrica se mantendrá siempre que se conserve la diferencia de potencial entre los extremos del conductor. Si queremos mantener la corriente circulando deberemos mantener la diferencia de potencial. Para mantener a la diferencia de potencial en estas circunstancias será necesario volver a enviar a los electrones que llegan al cuerpo positivo hacia el negativo. Para lograr este propósito se requerirá de otra forma de energía. Al dispositivo que permite mantener la diferencia de potencial entre dos puntos, aún cuando entre ellos circule una corriente se lo denomina generador eléctrico. + - Figura2.14 El tipo de energía utilizado, así como la manera de lograr el objetivo de mantener la diferencia de potencial entre los puntos depende de cada tipo de generador. Al de la figura 2.14 podríamos llamarlo “de puntapié”. Los hay químicos, como las baterías y las pilas. Los hay electromagnéticos; que son la mayoría de los utilizados a gran escala y que se clasifican según la energía con que se los Ing. Aldo Lugli Tancredi 17 EMBA Apuntes EB- Corriente continua mueve. Hidráulicos son aquellos electromagnéticos que se mueven mediante una corriente de agua. Eólicos si se mueven con el viento. Un micrófono dinámico es un generador del tipo electromagnético movido por las variaciones de presión del aire. 1,5V Bornes Figura 2.15 La figura 2.15 muestra los bornes de una batería de 9V y los de una pila de 1,5V A los puntos entre los que un generador mantiene la deferencia de potencial, y mediante los cuales se lo conecta, se los denomina bornes o terminales. 2.6 Intensidad de corriente eléctrica. Hemos descrito a la corriente eléctrica y ahora resulta necesario medirla. Para ello se define una característica de la corriente eléctrica llamada intensidad de corriente. Llamamos intensidad de corriente a la cantidad de carga eléctrica que atraviesa una sección neta del conductor en cada unidad de tiempo, y que se representa con la letra I. La sección neta del conductor es la que se obtiene cortando al mismo con un plano normal a su eje (es decir un plano a 90º del eje del conductor). I= Q t 2.5.1 Donde I es la intensidad de corriente o intensidad, Q la cantidad de carga y t el tiempo. Si la carga se mide en culombio y el tiempo en segundo la intensidad se mide en ampere, que se representa con A (mayúscula por ser tomado este nombre de un apellido) 3 Trabajo y potencia eléctricos. Cuando un generador desplaza cargas por un conductor y se produce una variación o caída de potencial se realiza un trabajo. Y a partir de la definición de diferencia de potencial (página 8) podremos calcular el trabajo realizado como: W = VAB ⋅ Q 18 3.1 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua y como se define potencia como la cantidad de trabajo en cada unidad de tiempo, es decir la rapidez con que se realiza un trabajo, resulta: P= W t 3.2 donde P es la potencia y por la igualdad 3.1 resulta que: P= VAB ⋅ Q = VAB ⋅ I t 3.3 Con la diferencia de potencial medida en volts y la intensidad en amperes la potencia resultará en watts (W mayúscula ya que también se tomó de un apellido). 4 Circuito eléctrico, resistencia y ley de Ohm. Cuando se conectan generadores con dispositivos capaces de realizar trabajos a partir de la energía eléctrica, (lamparitas, motores, estufas o sistemas de sonido) se forman sistemas a los que generalmente se les denomina circuitos eléctricos. La línea larga representa al borne positivo Conductor Bornes Generador Cruce de conductores sin conectar Cruce de conductores conectados Figura 4.1 Para su análisis, diseño y comunicación se suelen dibujar diagramas que representan a los circuitos eléctricos. A los diagramas también se los llama circuitos.En esos diagramas se representan los componentes del circuito y sus conexiones. Veamos ahora algunos de los símbolos utilizados. La figura 4.1 muestra los símbolos utilizados para representar al generador, al conductor y su conexión. Con los elementos que hemos estudiado hasta ahora podremos plantear un circuito muy sencillo, un generador con sus bornes conectados con un conductor. El diagrama resultante será el de la figura 4.2. Ing. Aldo Lugli Tancredi 19 EMBA Apuntes EB- Corriente continua I Vg Figura 4.2 Los componentes son: un generador, del que se suele indicar el valor de la diferencia de potencial entre bornes y el conductor que une sus bornes. Ese conductor permitirá que circule una corriente, que representaremos con una flecha que indica su sentido, acompañada de un nombre que la identifica (puede representarse como una flecha que acompaña al conductor, en la figura 4.2 se representa a la corriente de las dos maneras). Recordemos que mientras el generador mantenga la diferencia de potencial, se mantendrá la corriente. A la diferencia de potencial se le suele llamar tensión o voltaje. Como se observará el sentido de la flecha contradice todo lo dicho hasta ahora respecto de la corriente. Se ha dicho que la corriente está formada por cargas negativas que circulan de negativo a positivo, y esta es la realidad física. Por muchos años se creyó que la corriente eléctrica estaba formada por cargas positivas que circulaban de positivo a negativo. El avance en el conocimiento del átomo demostró que estaban en un error. Sin embargo ambos fenómenos conducen a lo mismo y como hay muchas reglas utilizadas en la práctica de la electricidad que se basan en la antigua hipótesis ambos sentidos se utilizan indiferentemente. Al primero, es decir al que supone cargas negativas que circulan de negativo a positivo se le denomina sentido electrónico, mientras que al segundo se le llama sentido convencional. Ambos son igualmente útiles y como es la costumbre utilizaremos el sentido convencional, que es el utilizado en la figura 4.2. Georg Simon Ohm (circa 1827) descubrió la relación que hay entre la tensión y la intensidad de corriente en un circuito como el de la figura 4.2. Encontró que dado un conductor, la intensidad de corriente varía en forma proporcional a la tensión. Encontró también que dada una diferencia de potencial la intensidad varía con el conductor. Se define una propiedad de los conductores llamada resistencia. Resulta que la intensidad de corriente es inversamente proporcional a la resistencia. Finalmente puede escribirse la relación, denominada ley de Ohm como: I= 20 Vg R 4.1 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua en la que R es el valor de la resistencia del conductor. L A Figura 4.3 La resistencia del conductor depende de sus dimensiones físicas y del material con el que está construido. La resistencia del conductor en el análogo eléctrico del rozamiento mecánico. Dado un conductor cilíndrico, figura 4.3, en la que L es la longitud del mismo y A su sección neta, entonces: R= ρ⋅L A 4.2 El coeficiente ρ, depende del material con el que está hecho el conductor y se denomina coeficiente de resistividad. Está asociado a la movilidad de las cargas en el material, cuanto mayor es este coeficiente, mayor es la resistencia y menor la movilidad de las cargas. El valor del coeficiente de resistividad varía con la temperatura, aumentando con ésta generalmente. Se define α (coeficiente de temperatura), el que indica cuanto aumenta ρ por cada ºC. Por lo tanto si conocemos ρ a 20 ºC, a una temperatura T1 su valor será: ρ(T1) = ρ( 20º C) ⋅ (1 + α ⋅ ∆T) 4.3 donde ∆T = T1 − 20 4.4 La resistencia se mide en ohms, que se representa con la letra griega omega mayúscula (Ω). El coeficiente de resistividad se mide en ohm.metro (Ω.m) Ing. Aldo Lugli Tancredi 21 EMBA Apuntes EB- Corriente continua Figura 4.4 Una propiedad muy interesante de la resistencia de los conductores o resistencia eléctrica es que hace que la energía eléctrica se convierta en calor. Es análoga a la fricción en mecánica. Una estufa, una lámpara de iluminación y una plancha aprovechan justamente la resistencia de los conductores para generar calor a partir de la energía eléctrica. La figura 4.4 muestra dos símbolos utilizados para representar a la resistencia eléctrica en los diagramas. Todos los conductores presentan resistencia. Los hay con muy poca y son los preferidos para llevar la energía eléctrica desde el generador hasta su destino. Los hay con mucha y se los prefiere para generar calor. 1 3 R1 R3 Vg R2 2 4 Figura 4.5 Los dispositivos construidos especialmente para aprovechar la propiedad resistencia se denominan resistores o resistencias y se los utiliza en circuitos electrónicos para construir filtros y atenuadores entre otras aplicaciones. Cuando se conectan resistencias con generadores, se utilizan conductores cuya resistencia es muy inferior a la puesta para, por ejemplo, generar calor. El diagrama sería el de la figura 4.5, en él Vg es el valor de la tensión entregada por el generador, R3 es la resistencia conectada para generar calor, R1 y R2 son las resistencias de los conductores que conectan al generador con la estufa. Generalmente sucede que las resistencias R1 y R2 son de valor despreciable frente al de R3. En ese caso directamente no se las tiene en cuenta y se supone, para simplificar el 22 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua análisis, que los conductores que unen los puntos 1 con 3 y 2 con 4 son perfectos, es decir que no tienen resistencia. El diagrama resultaría como en la figura 4.6. 1 3 R3 Vg 2 4 Figura 4.6 La resistencia de los conductores utilizados para conectar generadores con resistores suele despreciarse. Analicemos ahora que sucede cuando se conecta, en las condiciones planteadas en el diagrama de la figura 4.6, un generador a una resistencia. Circulará una corriente eléctrica que al atravesar la resistencia R3 generará calor. Este trabajo mediante el que la energía eléctrica se convirtió en calor necesariamente producirá una caída de potencial a las cargas. Es decir en el punto 3 el potencial será mayor que en el punto 4. Como suponemos que la resistencia de los conductores es nula, entonces la corriente, al circular por ellos no realizará ningún trabajo y entre los puntos 1 y 3 así como entre los 2 y 4 no habrá caída de potencial. Entonces toda la elevación de potencial que produce el generador, caerá en R3. Al ir del punto 2 al 1 las cargas reciben un aumento de potencial igual a la caída que sufren al ir de 3 a 4. En otras palabras, toda la energía de potencial que reciben en el generador la entregan en la resistencia sobre la que realizan un trabajo. Esto es análogo a la represa. El agua acumulada en el lago, gracias a la energía que recibió del sol (véase la página 9), realiza un trabajo al caer perdiendo esa energía. La resistencia conectada al generador para hacer que la corriente eléctrica realice un trabajo se suele denominar resistencia de carga o carga. En la resistencia la energía eléctrica se convierte en calor, que se disipa en el ambiente. Se dice entonces que la energía es disipada por la resistencia. La cantidad de energía disipada por la resistencia se puede calcular a partir de las expresiones ya planteadas. W = V3− 4 ⋅ Q = V3− 4 ⋅ I ⋅ t 4.5 en donde W es el trabajo o la energía disipada en la resistencia, V3-4 es la tensión o diferencia de potencial entre los extremos de la resistencia, Q es la cantidad de carga transportada, I la intensidad de corriente que circula por la resistencia y t es el tiempo que se, mantuvo conectada la resistencia al generador. Ing. Aldo Lugli Tancredi 23 EMBA Apuntes EB- Corriente continua A la corriente que circula por la resistencia de carga se la suele denominar corriente de carga. La rapidez con que se realiza el trabajo se denomina potencia y en el caso de la resistencia se la llama potencia disipada, pues como la energía se convierte en calor, esta se disipa en el ambiente. La potencia disipada puede calcularse mediante la expresión 3.3 y resultará. P = V3−4 × I 4.6 La ley de Ohm se puede expresar de tres maneras diferentes, que se deducen de la expresión 4.1 I= V R ; R= V I ; V = I×R ; V2 P= R Y sustituyendo en 4.6 resulta: P = I ×R 2 Expresiones que permiten calcular la potencia disipada en una resistencia conociendo su valor y el de la tensión o la corriente en la resistencia. Figura 4.7 La figura 4.7 permite recordar con facilidad las igualdades correspondientes a la ley de Ohm. Tapando la variable incógnita se puede observar la expresión para calcularla. La tabla 1 presenta un resumen de las fórmulas que relacionan tensión, corriente, resistencia y potencia disipada en la misma. 24 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua V = R×I I=V V = P×R I= P V=P I=P I R V R R =V R=V R= P P = V×I I 2 P 2 I P = I2 × R P=V 2 R Tabla 1 Figura 4.8 Imaginemos ahora a una persona arrastrando un objeto pesado por un camino. El trabajo que realice esta persona dependerá de la masa del objeto, de la longitud del camino, de la aspereza del camino y de la velocidad a la que se desplace. El rozamiento del cuerpo con el camino generará calor. El estudiante deberá asociar estas ideas con la resistencia, la intensidad de corriente y la diferencia de potencial. Ejercicios de aplicación y repaso. Tabla de coeficientes de resistividad Material Aluminio Cobre electrolítico Cobre industrial Hierro Oro Plata Plomo Manganina Niquelina Kanthal ρ resistividad a 20 ºC (Ω.m.10-8) 2,62-2,8 1,66-1,7241 1,83 9,9-11 2,44 1,62 21,9 42-44 33-45 135-152 (a 1300 ºC) α Coeficiente de temperatura 3,9.10-3 3,9.10-3 4,1.10-3 5,5.10-3 3,4.10-3 4.10-3 4,2.10-3 0,2.10-3 Ing. Aldo Lugli Tancredi 25 EMBA 4.1 Apuntes EB- Corriente continua ¿Qué resistencia presentará un trozo de alambre de hierro de 2 mm2 de sección y 30 m de longitud, a 20º C? Tomando el valor necesario de la tabla de coeficientes de resistividad y llevando los datos a las unidades correspondientes, metros en este caso, resulta: R= 4.2 9,9 × 10 −8 × 30 = 1,485 Ω 2 × 10 −6 ¿Qué resistencia presentará un trozo de alambre de cobre industrial de 2 mm2 de sección y 30 m de longitud, a 20º C? 1,83 × 10 −8 × 30 R= = 0,2745 Ω 2 × 10 −6 4.3 4.4 4.5 Calcular la resistencia de un alambre de niquelina de 1,5 mm2 de sección y 12 m de longitud a 20º C. Determinar que longitud de alambre de cobre industrial de 1 mm2 de sección se necesita para construir una resistencia de 4 Ω (a 20º C). ¿Qué resistividad presentará la plata a 130 ºC? Tomando los datos de la tabla y aplicando la fórmula 4.3 resultará ρ(130º ) = 1,62 × 10 −8 ⋅ (1 + 4 × 10 −3 × 110) = 2,33 × 10 −8 Ω ⋅ m 4.6 Calcular la resistencia de un alambre de niquelina de 1,5 mm2 de sección y 12 m de longitud a 130º C. Las resistencias que se venden en los comercios de electrónica traen representado su valor con un código de colores de uso muy generalizado. Dicho código aparece como un conjunto de franjas pintadas en el cuerpo cilíndrico de las resistencias. 1a. cifra 2a. cifra 3a. cifra multiplicador tolerancia Figura 4.9 La figura 4.9 muestra la disposición de las franjas de colores para resistencias de 1 % de tolerancia. Las de 5 y 10 % de tolerancia no tienen la franja correspondiente a la tercera cifra. La siguiente tabla muestra el valor de los colores para cada franja. 26 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua Color Negro Marrón Rojo Naranja Amarillo Verde Azul Violeta Gris Blanco Plata Oro Dígito 0 1 2 3 4 5 6 7 8 9 Multiplicador 1 10 100 1.000 (1 k) 10.000 (10 k) 100.000 (100 k) 1.000.000 (1 M) Tolerancia 0,01 0,1 10% 5% 1% Por ejemplo, una resistencia cuyas cuatro franjas fueran (en el orden mostrado en las figuras) marrón, rojo, amarillo y oro, tendría un valor de 120000 Ω ± 5%. Es decir que su valor estaría comprendido entre 114000 y 126000 Ω Otro caso, una resistencia cuyas cinco franjas fueran (en el orden mostrado en las figuras) marrón, rojo, violeta, rojo y marrón, tendría un valor de 12700 Ω ± 1%. Es decir que su valor estaría comprendido entre 12573 y 12827 Ω 4.7 4.8 4.9 4.10 4.11 4.12 ¿Cómo serán los colores de las franjas de una resistencia de 33kΩ y 5% de tolerancia? ¿Cómo serán los colores de las franjas de una resistencia de 12,5kΩ y 1% de tolerancia? ¿Cuál será el valor de una resistencia cuyas franjas sean marrón, negro, negro, oro y marrón? ¿Cuál será el valor de una resistencia cuyas franjas sean amarillo, violeta, negro, y plata? ¿Cuál será el valor de una resistencia cuyas franjas sean azul, gris, azul, naranja y marrón? En el diagrama correspondiente, la tensión del generador es 1,5 V y la resistencia es de 47 Ω. Calcular la intensidad de corriente entregada por el generador y la potencia disipada en la resistencia. Aplicando la ley de Ohm resultará que: I= y la potencia será Vg 1,5 = = 0,0319 A R 47 P = V ⋅ I = 1,5 ⋅ 0,0319 = 0,04785 W 4.13 Repetir el ejercicio 4.12 pero para una tensión de 9 V y una resistencia de 120 Ω. Cuando, como en los cálculos anteriores resultan valores mucho más pequeños que la unidad (o mucho más grandes, como ya veremos) se utilizan prefijos multiplicadores. La siguiente tabla nos muestra sus nombres, símbolos y valores. Ing. Aldo Lugli Tancredi 27 EMBA Apuntes EB- Corriente continua Factor Prefijo Símbolo 109 1.000.000.000 giga G 106 1.000.000 mega M 103 1.000 kilo k 102 100 hecto h 101 10 deca da 100 1 unidad 10-1 1/10 deci d -2 1/100 centi c -3 1/1.000 mili m -6 10 1/1.000.000 micro µ 10-9 1/1.000.000.000 nano n 10-12 1/1.000.000.000.000 pico p 10 10 El valor de intensidad resultante en el ejercicio 4.12 será entonces: 0,0319 A = 31,9 mA y la potencia será: 0,04785 W = 47,85 mW que se leen, respectivamente, mili amper y mili watt. 4.14 4.15 4.16 4.17 4.18 4.19 4.20 4.21 Convertir a ampere las siguientes cantidades: 125 mA; 24 µA (este símbolo, µ, es la letra griega micrón minúscula y significa micro); 2 kA. Convertir a ohm las siguientes cantidades: 68 kΩ; 1,5 MΩ; 58 mΩ, Convertir a volt las siguientes cantidades: 45 mV, 129 µV; 0,220 kV; 110000 mV. Convertir a mili ampere las siguientes cantidades: 0,0010 A; 0,0569 A; 12,5 A Convertir a mili volt las siguientes cantidades: 65 V; 0,005 V; 0,000045 V;48 V. Convertir a kilo ohm las siguientes cantidades: 600 Ω; 1680 Ω; 0,47 Ω; 60000 Ω. Calcular que valor tendrá la resistencia por la que circula una corriente de 120 mA si se produce una diferencia de potencial entre sus terminales de 48 V. Calcular que potencia se disipará en una resistencia de 12 kΩ si por ella circula una corriente de 0,02 mA. Siempre deberán hacerse los cálculos escribiendo las cantidades en las unidades respectivas. Veamos el ejercicio 4.20, aplicando la ley de Ohm, la resistencia se calculará como: R= 28 V 48 = = 400 Ω I 0,120 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua es decir, si la unidad está precedida de un prefijo, para hacer los cálculos el valor deberá multiplicarse por el factor correspondiente dado en la tabla anterior. Por ejemplo, la intensidad del ejercicio 4.12 que es de 0,02 mA deberá convertirse a amper multiplicándola por 10-3 ó por 0,001. Entonces resultará 0,02 mA = 0,02 × 10 −3 A = 0,00002 A = 2 × 10 −5 A 4.22 4.23 4.24 4.25 4.26 4.27 4.28 5 Calcular que tensión se desarrollará en una resistencia de 1,8 kΩ, si por ella circula una corriente de 0,5 A. Calcular que tensión se desarrollará en una resistencia de 2,2 kΩ, si por ella circula una corriente de 120 mA. Calcular que potencia se disipará en una resistencia de 1300 Ω, si por ella circula una corriente de 0,5 A. Calcular que potencia se disipará en una resistencia de 3,3 kΩ, si por ella circula una corriente de 12 mA. Calcular el valor de la resistencia a la que aplicándole una tensión de 25 V disipa 12 W. Expresar el resultado en mΩ, Ω y kΩ ¿Qué resistencia presentará una lámpara que alimentada con 100 V disipa una potencia de 25 W? ¿Qué cantidad de trabajo realizará la corriente eléctrica al circular por la lámpara del ejercicio anterior por durante 1:25:30 hr? (atención, el tiempo en horas está dado en forma sexagesimal) Combinación de elementos. Es común que un circuito eléctrico esté formado por varios elementos conectados entre si. Pensemos en una casa y veremos que además de varias lamparitas conectadas al mismo generador (la compañía distribuidora de energía eléctrica) y que se prenden o apagan individualmente tenemos motores, televisores, etc. etc. Un circuito de estas características es más complicado que lo visto hasta ahora. Para poder analizar sistemas más complejos se dispone de herramientas que permiten simplificar los circuitos. Definamos equivalencia de circuitos. Dos circuitos son equivalentes si sustituyendo uno por otro en un sistema más complejo, el resto de las variables se mantienen sin cambio. I Vg Red compuesta por varios elementos I Vg Req Figura 5.1 Veamos el significado de esta definición en la figura 5.1. Ing. Aldo Lugli Tancredi 29 EMBA Apuntes EB- Corriente continua Supongamos que tenemos un sistema eléctrico complejo conectado a un generador que entrega una tensión de Vg volt y una corriente de intensidad I. Si al sustituir ese sistema eléctrico complejo por una resistencia, manteniendo al generador sin cambios, la corriente que circula es de igual intensidad, entonces la nueva resistencia es equivalente al sistema eléctrico complejo. 5.1 Conexión serie. Ra Rb I Vg Figura 5.2 Dos o más elementos eléctricos están conectados en serie si el terminal de salida de uno de ellos está conectado al de entrada de otro y así sucesivamente. La figura 5.2 muestra tres elementos conectados en serie. La intensidad de corriente es la misma en cada elemento de los conectados en serie. Llamaremos nudo o nodo al punto de conexión de dos o más elementos eléctricos. A B Figura 5.3 En la figura 5.3 claramente el punto A es un nudo, según la definición. En la misma figura la zona encerrada por la línea de puntos (B) también es un nudo. Puede ampliarse la definición diciendo que un nudo es un conjunto de puntos, de un circuito, que tengan el mismo potencial. 30 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua Normalmente se elige un nudo como referencia de potenciales dentro del circuito, es decir potencial cero (recuérdese la referencia de alturas, en la página 6). Figura 5.4 A ese nudo se lo denomina común o tierra y se lo suele representar de las maneras que muestra la figura 5.4. A 3 B C 1 2 Figura 5.5 Llamaremos malla a todo posible camino cerrado para la corriente eléctrica. En la figura 5.5 podemos identificar primero conceptos ya planteados. El circuito tiene tres nudos (A, B, y C). El punto 1 corresponde al nudo B y los puntos 2 y 3 corresponden al nudo C que a su vez es la referencia. Veamos ahora las mallas. Hay tres mallas que son los caminos cerrados A, B, C, 3, A; B, 1, 2, C, B y A, 1, 2, 3, A. Ing. Aldo Lugli Tancredi 31 EMBA 5.2 Apuntes EB- Corriente continua Ley de Kirchhoff de las tensiones. La suma de las subidas de potencial es igual a la suma de las caídas de potencial tomadas a lo largo de una malla. VAB A B R1 Vg IA R2 VBC C Figura 5.6 En la figura 5.6 observamos dos resistencias (R1 y R2) conectadas en serie con un generador (Vg). En estas condiciones circulará una corriente (Ia). La corriente realizará un trabajo en cada resistencia que se manifestará con una caída de potencial en cada una de ellas (VAB y VBC). Por otra parte el generador provocará una subida de potencial a las cargas al ser trasladadas desde C hasta A. Entonces, en virtud de la ley de Kirchhoff de las tensiones podremos escribir: Vg = VAB + VBC 5.2.1 pero, de acuerdo a la ley de Ohm Vg = Ia × R1 + Ia × R 2 5.2.2 La cantidad de carga que sale del borne positivo del generador ha de ser igual a la que entra por el negativo (hablamos de corriente en el sentido convencional), por lo tanto la corriente será igual en todos los puntos de la malla de la figura 5.6. Es decir, en la ecuación 5.2.2 podremos poner a Ia como factor común, resultando: Vg = Ia × (R1 + R 2) 5.3 5.2.3 Equivalente serie. Veamos ahora como calcular el valor equivalente de dos resistencias en serie. Estos cálculos nos permitirán analizar redes más amplias como pueden ser las redes de parlantes en un sistema de amplificación o de distribución de sonido. Si una resistencia es equivalente a las conectadas en serie en la figura 5.6, entonces sustituyendo a R1 y R2 por esa, la corriente no habrá de variar si no varía la tensión. En la figura 5.7 hemos sustituido a R1 en serie con R2 por la equivalente supuesta Reqs. 32 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua Entonces si Vg es del mismo valor en las figuras 5.6 y 5.7, la corriente Ia tendrá también el mismo valor. Por la ley de Ohm Reqs. Se puede calcular como: Re qs = Vg Ia 5.2.4 Y sustituyendo por la ecuación 5.2.4 resulta: Re qs = R1 + R 2 5.2.5 A IA Vg Reqs C Figura 5.7 El valor equivalente de dos resistencias conectadas en serie es la suma de sus valores. El alumno deberá analizar si este resultado se puede aplicar a cualquier número de resistencias en serie. 5.3 Divisor de tensión. A B R1 Vg IA R2 V2 C Figura 5.8 Un circuito con muchas aplicaciones en audio es el formado por dos resistencias en serie y que se denomina divisor de tensión. Ing. Aldo Lugli Tancredi 33 EMBA Apuntes EB- Corriente continua En la figura 5.8 tenemos un divisor de tensión formado por las resistencias R1 y R2 y nos interesa conocer el valor de la tensión desarrollada en una de ellas, R2, a la que llamaremos V2. Véase que la tensión que hemos llamado V2 es la que aparece entre los nudos B y C, podríamos llamarla también VBC. Aplicando la ley de Ohm resulta que: V 2 = Ia × R 2 5.3.1 Por otra parte la corriente Ia puede ser calculada también por la misma ley conociendo la resistencia equivalente de la serie. Es decir: Ia = Vg Vg = Re qs R1 + R 2 5.3.2 y sustituyendo este valor de Ia en la ecuación 5.3.1 resulta: V2 = Vg R2 × R 2 ó V 2 = Vg × R1 + R 2 R1 + R 2 5.3.3 El estudiante deberá verificar que la fórmula para el cálculo de la tensión desarrollada entre los terminales de R1 es: V1 = Vg × A R1 R1 + R 2 V1 B R1 IA Vg R2 V2 C Figura 5.9 Sigamos con el circuito serie. La corriente Ia es la misma en ambas resistencias. Suponemos que en R2 se desarrolla la tensión V2 y que en R1 se desarrolla V1. Entonces por la ley de Ohm resultará: Ia = 34 V1 V 2 V1 R1 = = y por lo tanto V 2 R2 R1 R 2 Ing. Aldo Lugli Tancredi 5.3.4 EMBA Apuntes EB- Corriente continua En un circuito serie las tensiones desarrolladas en cada resistencia son directamente proporcionales a las resistencias. Un aplicación práctica del divisor de tensión es el fader cuyas dos resistencias varían con el movimiento de la perilla. A Contacto móvil C B Pista resistiva Figura 5.10 a El fader está constituido por una barra de material conductor de alta resistividad, (figura 5.10 a) llamada pista. En los extremos de la pista hay dos conductores que la conectan con el resto del circuito ( A y C). Un contacto móvil que se desliza a lo largo de la superficie de la pista mediante la perilla también está conectado al resto del circuito mediante el conductor B. La resistencia entre los extremos de la pista normalmente es del orden de decenas de kiloohm. La figura 5.10 b nos muestra un circuito equivalente al mecanismo mostrado en la figura 5.10 a. Las resistencias RAB y RBC representan respectivamente el valor de resistencia comprendida entre el extremo A y el contacto móvil B y el valor de la que hay entre el contacto móvil y el extremo C. Compárese con la figura 5.8 y veremos que el fader es un divisor de tensión en el que aplicamos una tensión entre los puntos A y C y obtenemos una entre los puntos B y C. A RAB Contacto móvil B Pista RBC C Figura 5.10 b Ing. Aldo Lugli Tancredi 35 EMBA Apuntes EB- Corriente continua Si ahora movemos el contacto móvil hacia el extremo A la resistencia RAB disminuirá mientras que la resistencia RBC aumentará. El estudiante deberá razonar como varía la tensión entre los terminales B y C cuando desplazamos el contacto móvil desde C hacia A y viceversa (supóngase constante la tensión entre A y C) 5.4 Conexión paralelo. Dos o más elementos eléctricos están conectados en paralelo si los terminales de salida de todos ellos están conectados en un nudo y los de entrada en otro. Figura 5.11 La figura 5.11 muestra tres resistencias conectadas en paralelo Todos los elementos conectados en paralelo están sometidos a la misma diferencia de potencial. 5.5 Ley de Kirchhoff de las corrientes. La suma de las intensidades de las corrientes que entran en un nudo es igual a la suma de las intensidades de las corrientes que salen del mismo. It Vg I1 R1 I2 R2 Figura 5.12 36 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua En la figura 5.12 observamos dos resistencias (R1 y R2) conectadas en paralelo con un generador (Vg). En estas condiciones circulará una corriente total (It) que se repartirá entre R1 y R2. Entonces, de acuerdo a la ley de Kirchhoff de las corrientes podremos escribir: It = I1 + I2 5.5.1 pero, de acuerdo a la ley de Ohm It = VG VG + R1 R2 5.5.2 Y dado que la diferencia de potencial entre los terminales de todos los elementos que están en paralelo es la misma, entonces en la ecuación 5.5.2 podremos poner como factor común a VG de lo que resultará: It = VG × ( 5.6 1 1 + ) R1 R2 5.5.3 Equivalente paralelo. It Vg Reqp Figura 5.13 Veamos ahora como calcular el valor equivalente de dos resistencias en paralelo. Si una resistencia es equivalente a las conectadas en paralelo en la figura 5.12, entonces sustituyendo a R1 y R2 por esa, la corriente no habrá de variar si no varía la tensión. En la figura 5.13 hemos sustituido a R1 en paralelo con R2 por la resistencia equivalente supuesta Reqp. Entonces si Vg es del mismo valor en las figuras 5.12 y 5.13, la corriente It tendrá también el mismo valor. Por la ley de Ohm Reqp se puede calcular como: Re qp = Vg IT 5.6.1 Y sustituyendo por la ecuación 5.5.3 resulta: Ing. Aldo Lugli Tancredi 37 EMBA Apuntes EB- Corriente continua Re qp = 1 5.6.2 1 1 + R1 R 2 El alumno deberá verificar que este resultado se puede aplicar a cualquier número de resistencias en paralelo, con lo que: La resistencia equivalente de varias conectadas en paralelo es una cuyo valor es igual a la inversa de la suma de las inversas de los valores individuales. Haciendo común denominador en el denominador de la expresión 5.6.2 y simplificando resultará: Re qp = R1 × R 2 R1 + R 2 6.5.3 Es importante tener en cuenta que esta última fórmula es aplicable solamente a dos resistencias en paralelo. En este momento es útil definir la conductancia a la que representaremos con la letra G. Llamaremos conductancia a la inversa de la resistencia, es decir: G= 1 R 6.5.4 La conductancia se mide en siemen que se representa con la letra S. De esta manera: 1S = 1 1Ω 6.5.5 Sustituyendo R por 1/G en la ecuación 6.5.2 resultará: Geqp = G1 + G 2 6.5.6 La conductancia equivalente de un conjunto de resistencias conectadas en paralelo es la suma de las conductancias individuales. 38 Ing. Aldo Lugli Tancredi EMBA 5.7 Apuntes EB- Corriente continua Divisor de corriente. La figura 5.14 nos muestra dos resistencias en paralelo. Puede resultar útil calcular una corriente, ya sea I1 o I2 como función de la corriente total y las resistencias. R1 I1 It I2 R2 Figura 5.14 Dado que las resistencias están en paralelo, las diferencias de potencial entre sus terminales serán iguales. Llamémosle Vp a dicha diferencia de potencial y aplicando la ley de Ohm resulta que: Vp = IT × Re qp = IT × La corriente I1 será: I1 = R1 × R 2 R1 + R 2 Vp R2 = IT × R1 + R 2 R1 5.7.1 5.7.2 Por otra parte, como la tensión en cada resistencia es la misma, podremos escribir que: Vp = I1 × R1 = I 2 × R 2 entonces: I1 I2 = R 2 R1 5.7.3 En un circuito formado por dos resistencias en paralelo, las intensidades de corriente de cada resistencia son inversamente proporcionales a las resistencias. Ing. Aldo Lugli Tancredi 39 EMBA 5.8 Apuntes EB- Corriente continua Generador real. Por lo visto hasta ahora parecería que la tensión que entrega entre terminales un generador es una constante independiente de la intensidad de corriente que dicho generador entregue a la carga. Este comportamiento puede atribuírsele a un generador ideal. Vg Generador ideal Generador real IL 0 Figura 5.15 Un generador real entregará una tensión que disminuirá al aumentar la intensidad de la corriente de carga. La figura 5.15 nos muestra gráficamente ambas situaciones. La del generador ideal cuya tensión no varía con la carga y la del real, cuya tensión disminuye con el aumento de la carga. Fácilmente podremos demostrar que un generador ideal no puede existir. Obsérvese que en todo momento la potencia entregada por el generador será: Po = Vg × IL 5.8.1 Si se tratara de un generador ideal Vg se mantendría constante para cualquier valor de IL por más que esta aumentara. La potencia podría aumentar indefinidamente y con ella la energía entregada. Un generador ideal podría entregar energía sin límites. Lindo sueño, pero imposible. Tal dispositivo no existe y es, como lo llamáramos, ideal. Veamos ahora como puede construirse un modelo del generador real a partir de los elementos que estudiamos. La figura 5.16 muestra el modelo (encerrado en la línea de trazos) que consta de un generador ideal que entrega una tensión llamada Vgoc, en serie con una resistencia (Rg). Los bornes del generador real son A y B y la tensión entregada por el mismo es Vg. 40 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua A Rg Vgoc Vg B Figura 5.16 Si no conectamos una carga al generador real, no circulará corriente por Rg y la tensión Vg será igual a Vgoc (no habrá caída de potencial en Rg). En estas condiciones se dice que el generador se encuentra en circuito abierto. Dado un generador real podremos construir un modelo que lo represente con un generador ideal que entregue una tensión igual a la que entrega el generador real en circuito abierto. El apelativo oc es la abreviatura de open cirquit (circuito abierto en inglés). Veamos ahora que sucede al conectarle una carga al generador real (figura 5.17). A IL Rg Vgoc Vg RL B Figura 5.17 Ahora tendremos una corriente de carga IL provocada por la conexión de RL al generador. Tal corriente producirá una caída de potencial en Rg haciendo que la tensión Vg ya no sea igual a Vgoc. Queda claro que cuanto mayor sea IL mayor será la caída en Rg y menor será Vg. Esto coincide con el gráfico de la figura 5.15. A la caída de potencial en Rg se le denomina caída interna. Si tenemos en cuenta que RL y Rg están en serie con el generador ideal, veremos que ambas resistencias forman un divisor de tensión, y aplicando la ecuación 5.3.3 resultará: Ing. Aldo Lugli Tancredi 41 EMBA Apuntes EB- Corriente continua Vg = Vgoc × RL Rg + RL 5.8.2 A Rg Vgoc Vg Isc B Figura 5.18 La idea de presentar a un generador real con este modelo es muy difundida y estudiando las especificaciones de micrófonos profesionales podremos encontrar como datos la tensión en circuito abierto y la resistencia interna. Es necesario que el estudiante lo verifique leyendo especificaciones reales de micrófonos. A la resistencia interna de un generador también se le denomina resistencia de salida. Si los bornes del generador se conectan con un conductor de resistencia nula, figura 5.18 se dice que su salida está en cortocircuito. En ese caso la tensión del generador será prácticamente nula y la corriente de carga será la máxima posible o corriente de cortocircuito, Isc. El valor de dicha corriente será: Isc = Vgoc Rg 5.8.3 De lo que resulta que: Rg = Vgoc Isc 5.8.4 Determinar el valor de la resistencia Rg por este método puede resultar impráctico y hasta destructivo, pues al poner al generador en corto circuito podemos hacer que este entregue más potencia de la que es capaz y se destruya. Una manera práctica de medir la resistencia interna de un generador sin necesidad de medir la corriente de corto circuito es la siguiente. Primero medimos la tensión de salida en circuito abierto. Luego cargamos al generador con una resistencia conocida y volvemos a medir la tensión de salida Vg. Véase la figura 5.17 en la que Vgoc, RL y Vg son conocidos. Entonces: Rg = 42 Vgoc − Vg I Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua y dado que I= Vg RL resultará: Rg = Vgoc − Vg Vgoc − Vg × RL = Vg Vg RL Es conveniente aclarar que los resultados de estos cálculos serán más confiables si RL es del orden de Rg, lo que puede exigir al generador una potencia mayor de la que es capaz de entregar. Puede resultar una medición destructiva tratándose de generadores de gran potencia. Ing. Aldo Lugli Tancredi 43 EMBA Apuntes EB- Corriente continua Ejercicios de aplicación y repaso. En los ejercicios siguientes y a menos que se especifique lo contrario, los conductores que conectan los diversos dispositivos tienen resistencias despreciables, y los generadores tienen resistencia interna también despreciable. 5.1 Conectar con trazos de manera que las cuatro resistencias resulten en serie. A A A A B B B B Ejercicio 5.1 5.2 5.3 Si las cuatro resistencias del ejercicio anterior fueran respectivamente de 600 Ω; 1,2 kΩ; 0,005 MΩ y 12500 mΩ, calcular el valor de la resistencia equivalente. Conectar con trazos de manera que las cuatro resistencias resulten en paralelo. A A A A B B B B Ejercicio 5.3 5.4 5.5 5.6 44 Si las cuatro resistencias del ejercicio anterior fueran respectivamente de 2.200 Ω; 3,3 kΩ; 47.000.000 mΩ y 0,01 MΩ, calcular el valor de la resistencia equivalente. Un conductor presenta una conductancia de 12,5 S, calcular su resistencia. Dos resistencias están conectadas en paralelo a un generador de 24 V. Una de ellas es de 600 Ω y la otra es de 1,2 kΩ. Dibujar el circuito, calcular la corriente que entrega el generador y la potencia disipada en cada resistencia. Ing. Aldo Lugli Tancredi EMBA 5.7 5.8 5.9 5.10 5.11 5.12 5.13 5.14 Apuntes EB- Corriente continua Calcular el valor de una resistencia cuyas franjas sean naranja, naranja, roja y plata. Si por tres resistencias conectadas en serie, una de 330 Ω, otra de 680 Ω y la tercera de 2,2 kΩ circula una corriente de 20 mA calcular la tensión entre los extremos de la serie. Dibujar el circuito. En el ejercicio 5.8 calcular la potencia disipada en cada resistencia. En que momento una lámpara incandescente presentará su máxima resistencia, ¿cuando está fría o caliente? ¿Cómo conecta dos resistencias para que presenten la máxima resistencia posible? ¿Cómo conecta dos resistencias para que disipen la máxima potencia posible? Un generador entrega 9 V en circuito abierto y 8,4 con una carga de 16 Ω. Calcular la resistencia interna del mismo. Dibuje el circuito equivalente del generador. La figura correspondiente a este ejercicio nos presenta un nuevo problema. Algunas resistencias están conectadas en serie y otras en paralelo. A estos circuitos se los llama mixtos. 100 Ω A 330 Ω B 47 Ω 470 Ω 15 V Ejercicio 5.14 Hay que observar cuidadosamente el diagrama porque en ocasiones puede ser confuso. Una manera de comenzar a analizarlos es caminando por el conductor a partir de un terminal de la fuente, cuando al salir de un elemento (sea generador o resistencia) entramos en otro, estarán en serie. Si al salir de un elemento encontramos que el camino se divide y podemos entrar a más de un elemento, entonces estamos frente elementos en paralelo. Este conjunto de elementos en paralelo terminará cuando los caminos se vuelvan a juntar. En la figura ejercicio 5.14, si partimos del terminal positivo del generador encontraremos una resistencia de 47 Ω al salir de la cual encontramos una de 100 Ω que está en serie con la primera y con el generador. Desde la salida del generador hasta el punto A podremos simplificar el circuito sustituyendo ambas resistencias por su equivalente serie, figura ejercicio 5.14-b. Seguidamente el camino se bifurca y encontramos dos resistencias, una en cada rama del camino. Las dos ramas del camino vuelven a juntarse en el punto B. Tenemos entonces dos resistencias en paralelo, una de 330 Ω y otra de 470 Ω entre los puntos A y B que pueden ser sustituidas por su equivalente como en la figura ejercicio 5.14-b. Ahora resultan dos resistencias en serie con el generador que fácilmente se sustituyen por una equivalente en la figura ejercicio 5.14-c. Ing. Aldo Lugli Tancredi 45 EMBA Apuntes EB- Corriente continua A 147 Ω 340,87 Ω 139,87 Ω B 15 V 15 V Ejercicio 5.14 b Ejercicio 5.14 c Podemos entonces calcular la corriente que entrega el generador, que será: Ig = 15 = 44 mA 340, 87 Puede ahora calcularse la potencia entregada por el generador, que será igual a la suma de las potencias disipadas por todas las resistencias del circuito. El alumno deberá calcularla y dibujar en los tres circuitos equivalentes la flecha que represente la corriente Ig. Si pasamos al circuito 5.14-b podremos calcular, mediante las ecuaciones del divisor de tensión, la tensión en cada resistencia y así en el primer circuito podremos calcular la corriente en cada resistencia del paralelo y las potencias disipadas en cada una. 5.15 En la figura ejercicio 5.15 calcular las potencias disipadas en cada resistencia. 1k5Ω 220 Ω 12 V 860 Ejercicio 5.15 5.16 46 Una aplicación muy común e importante de lo que acabamos de ver es el análisis del comportamiento de redes de parlantes. Una aproximación útil consiste en suponer al parlante como una resistencia (más adelante veremos que en realidad es más complejo) lo que permite hacer una predidcción rápida del comportamiento de una red más o menos compleja. Las especificaciones de los parlantes incluyen, entre otras muchas, el valor de su resistencia nominal, que es la que se usa en este caso. Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua Seguramente ya habrán oído hablar de parlantes de 4, 8 ó 16 Ω. La figura correspondiente a este ejercicio nos presenta una red de parlantes de la que se pide calcular la resistencia equivalente entre los puntos A y B. 8Ω 8Ω B 16 Ω 8Ω 8Ω A Ejercicio 5.16 5.17 Dibuje una red conformada con cuatro parlantes de 8 Ω de manera que en total presenten una resistencia de 8 Ω. 5.18 En el circuito de la figura correspondiente calcule la tensión entre los puntos A y B, y la intensidad Ia. 820 Ω 560 Ω Ia 680 Ω 470 Ω 25 mA B A Ejercicio 5.18 Ing. Aldo Lugli Tancredi 47 EMBA 6 6.1 Apuntes EB- Corriente continua Efectos de la corriente eléctrica. Efecto térmico o efecto Juole. El efecto térmico, que ya ha sido mencionado, es posiblemente la aplicación más común y más sencilla de la corriente eléctrica. Las partículas que componen la materia están sometidas, por efecto del calor, a un movimiento desordenado, llamado agitación térmica. Si la temperatura disminuye este movimiento se hace menor. Se denomina cero absoluto a la temperatura en la que las partículas pierden todo movimiento, valor que se sitúa en -273 ºC y al que solo se puede aproximar en laboratorios. Es esta agitación térmica la causa de ruido que naturalmente presentan todos los sistemas electrónicos, llamado ruido térmico. Bien, al circular una corriente por un conductor las cargas en su movimiento chocan contra las moléculas del mismo aumentando el movimiento de estas y creando mayor cantidad de choques entre las partículas con lo que se genera calor (como cuando nos frotamos las manos) y aumenta la temperatura del conductor. El calor es la forma de energía que causa el aumento de temperatura, dos conceptos que conviene no confundir. Se llama caloría a la cantidad de calor que se necesita para aumentar en un grado Celsius un gramo de agua pura. Kilo caloría es la cantidad de calor necesaria para aumentar un grado Celsius la temperatura de un kilogramo de agua pura. El físico inglés Joule descubrió (circa 1840) que la cantidad de calor desprendida de un conductor por efecto de la circulación de una corriente eléctrica depende de la resistencia del mismo, de la intensidad de dicha corriente y del tiempo que se mantiene la corriente circulando. La potencia eléctrica puede calcularse, ecuación 4.4 y siguientes como P = I2 × R y dado que la potencia es la velocidad con que se transfiere la energía, es decir la velocidad con que se realiza un trabajo, entonces P= W ∴ W = P × t = I2 × R × t t 6.1 La energía se mide en julios o joules (precisamente en homenaje a Joule) y como la caloría es una unidad de cantidad de calor que también es una forma de energía hay una equivalencia entre julios y calorías, la cual resulta: 1J = 0,24cal 6.2 Supongamos que una corriente de 3 A circula durante 3 hr por una resistencia de 6 Ω. La cantidad de calor generado, Q será: Q = 0, 24 ⋅ 32 × 6 × 10800 = 139, 97 kcal La temperatura de un conductor por el que circula corriente aumentará hasta que la cantidad de calor generado sea igual a la que se entrega al ambiente. Se dice que el sistema está en equilibrio térmico. 48 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua En conductores destinados a conexiones deberá cuidarse la temperatura de trabajo para evitar que el aislante se descomponga y se destruya. En muchos casos un aumento excesivo de temperatura del aislamiento puede traer como efecto la emanación de gases tóxicos (causa común de afecciones personales en caso de incendio). Dependiendo de la sección del conductor, el material con que se compone el aislador y las condiciones de instalación se establece un valor de densidad de corriente máximo, es decir un valor máximo de intensidad de corriente por cada mm2 de sección. En la tabla siguiente, que está tomada de la página de Pirelli, se muestran las características de cables para distribución de energía eléctrica. Diametro Masa Intensidad Sección Diametro Espesor de de nominal máximo de aislación exterior aprox. aprox. nominal corriente alambres admisible del en cañerías conductor (1) Intensidad Caída de Resist. de corriente Tensión eléctrica admisible al (2) máxima a aire libre (1) 20ºC y CC mm² mm mm mm Kg/Km A A V/A km ohm/km 0,75 0,21 0,6 2,4 12 8 10 50 26 1,0 0,21 0,7 2,8 16 10,5 12 37 19,5 1,5 0,26 0,7 3,0 21 13 15,5 26 13,3 2,5 0,26 0,8 3,7 32 18 21 15 7,98 4 0,31 0,8 4,2 46 24 28 10 4,95 6 0,31 0,8 4,8 65 31 36 6,5 3,3 10 0,41 1,0 6,1 110 42 50 3,8 1,91 16 0,41 1,0 7,9 185 56 68 2,4 1,21 25 0,41 1,2 9,8 290 73 89 1,54 0,78 35 0,41 1,2 11,1 390 89 111 1,2 0,554 50 0,41 1,4 13,6 550 108 134 0,83 0,386 70 0,51 1,4 16,1 785 136 171 0,61 0,272 95 0,51 1,6 18,3 1000 164 207 0,48 0,206 120 0,51 1,6 19,7 1250 188 239 0,39 0,161 (1) 3 cables en cañerías embutidas en mampostería o en aire libre dispuestos en plano, temperatura ambiente 30 ºC. (2) Cables en contacto en corriente alterna monofásica 50 Hz., cos fi=0,8. Coeficientes de corrección de la corriente admisible: - Para dos cables en cañería multiplicar por 1,10 - En aire libre multiplicar por 1,12 - Para temperatura ambiente de 40 ºC multiplicar por 0,89 Una cuestión muy importante a tener en cuenta es la resistencia de contacto en las fichas y toma corriente de alimentación y empalmes eléctricos. Cuando los materiales eléctricos son de mala calidad o defectuosos, el contacto entre las distintas partes, como por Ing. Aldo Lugli Tancredi 49 EMBA Apuntes EB- Corriente continua ejemplo las patas del enchufe con el alojamiento o el empalme del cable de conexión en un componente cualquiera, pueden presentar un valor excesivo de resistencia. En ese caso la temperatura aumentará peligrosamente empeorando la situación y llegando en extremo a producirse un corto circuito por destrucción del aislante o incluyo encendido de materiales combustibles próximos, de los que hay abundancia en las instalaciones de tratamiento acústico en los estudios. Es necesario un cuidadoso mantenimiento preventivo de las instalaciones eléctricas eliminando todo componente defectuoso y nunca usar adaptadores. Fusibles. El fusible es un trozo de conductor de bajo punto de fusión, que se intercala en el circuito con el fin de proteger la instalación. En caso de exceso de corriente el fusible se fundirá por efecto Joule cortando el suministro. Según su construcción los hay más o menos rápidos (dependiendo del tipo de instalación que hay que proteger) debiéndose sustituir un fusible siempre por otro de iguales características al indicado por el fabricante del equipo, de lo contrario se corre el riesgo de producir mayores problemas. Nunca deberá sustituirse un fusible por un alambre, papel de chocolates o de atado de cigarrillos. Suele ser buen negocio para los técnicos de reparación. Todo equipo debería estar acompañado siempre de un juego de fusibles de repuesto y en caso de fusión de los mismos dos veces consecutivas deberá investigarse la causa y nunca cambiar el fusible por otro más grande. Tipos de fusibles. Los equipos electrónicos generalmente están protegidos por fusibles de forma de tubo de vidrio con casquillos metálicos en sus extremos. estos pueden ser de 20 ó 30 mm de longitud con un diámetro de 6mm aproximadamente. Los portafusibles están diseñados para alojar una sola de las longitudes. Instalar un fusible de 20 mm en un alojamiento de 30 mm impedirá que el fusible se conecte. Algunos portafusibles puestos en circuitos impresos (dentro del compartimiento de equipo) permiten la instalación de ambos tipos de fusible. 6.2 Efecto magnético. El imán realiza fuerzas, que al igual que las masas y las cargas eléctricas, no requieren de contacto físico con el objeto al que se aplica esa fuerza. Se dice que son fuerzas a distancia. En imán realizará fuerzas sobre otros imanes o sobre cuerpos de algunos materiales como por ejemplo el hierro (llamados en general ferromagnéticos). A la zona del espacio, que rodea al imán, en la que se realizan las fuerzas magnéticas se la denomina campo magnético. Al igual que con el campo eléctrico y el gravitatorio utilizaremos la representación ideada por M.Faraday de líneas de fuerza, con el mismo significado que tienen en los campos ya estudiados. El campo magnético es un campo cerrado, es decir el origen y el final de las líneas de fuerza que lo definen se hallan en el mismo cuerpo, a diferencia del campo eléctrico y el gravitatorio cuyas líneas se tienden entre cuerpos diferentes. Una barra de imán suspendida y libre para moverse se orientará de acuerdo al campo magnético terrestre, y al extremo que “busca” al norte se le denomina norte (otro tanto sucede con el que se orienta hacia el sur), figura 6.2.1. 50 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua N Figura 6.2.1 En la figura 6.2.2 podemos ver una representación del campo magnético de un imán con forma de barra. A las zonas del imán donde se concentran las líneas de fuerza se les denomina polos y es donde su fuerza es mayor. N S Figura 6.2.2 Las cargas eléctricas positiva y negativa pueden aislarse, los polos de un imán no pueden separarse. Si rompemos un imán obtendremos dos imanes más pequeños pero nunca separaremos sus polos. Así como para estudiar al campo eléctrico se utiliza una carga (positiva por convención) y se analiza el efecto de ese campo sobre la misma, para estudiar al campo magnético se observan los efectos de este sobre el polo norte de un imán. Puede utilizarse una brújula, que no es otra cosa que un imán en forma de barra muy fina y libre de moverse en el plano horizontal. Se comprueba experimentalmente que polos iguales se repelen y polos diferentes se atraen. Si movemos alrededor de un imán una brújula, la aguja de esta se desviará por efecto de la fuerza a la que la somete el imán. Al conjunto de las líneas de fuerza se le denomina flujo magnético (Φ) y la unidad de medida en el SI es el weber (Wb). La fuerza que hace el campo sobre un objeto es proporcional a la densidad de flujo magnético. La densidad de flujo magnético está determinada por la cantidad de líneas de fuerza por unidad de superficie (medida esta última en un plano perpendicular a las líneas de fuerza) . A medida que nos alejamos del cuerpo que genera el campo la densidad Ing. Aldo Lugli Tancredi 51 EMBA Apuntes EB- Corriente continua disminuye con el cuadrado de la distancia. La unidad de medida es el tesla (T) equivalente a un Wb por m2. Campo magnético producido por una corriente eléctrica. Alrededor de toda corriente eléctrica se genera un campo magnético. Las líneas de fuerza de este campo magnético tienen forma circular, con centro en el conductor y se desarrollan en un plano perpendicular a este, figura 6.2.3. Φ I Figura 6.2.3 A medida que nos alejamos del conductor las líneas de fuerza tienen menos densidad. Por otra parte la cantidad de flujo magnético es proporcional a la intensidad de corriente. Figura 6.2.4 Si imaginamos el corte de un conductor perpendicular a la hoja de papel (círculo central de la figura 6.2.4) por el que circula una corriente desde adelante hacia atrás de la hoja, las líneas de fuerza harían desplazarse al polo norte de un imán de prueba en sentido horario, como lo muestran las flechas de la misma figura. Es costumbre representar a la corriente que entra en el papel mediante una cruz (recuerda a la cola de una flecha). Si por el contrario, la corriente circulara desde atrás hacia delante, la representaremos mediante un punto como si fuera la punta de la flecha que viene hacia el lector. El sentido de rotación de las líneas de fuerza se puede determinar mediante la regla llamada “del tirabuzón”. Las líneas de fuerza girarán en el sentido que deba girar un tirabuzón que penetre a lo largo del conductor y avance en el sentido de la corriente eléctrica, figura 6.2.5. 52 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua Φ I Figura 6.2.5 Es importante aclarar que esta regla así como todas las reglas empíricas referidas a la corriente eléctrica están referidas al sentido convencional de circulación de la corriente. Esta es la razón por la que se siguen utilizando en la actualidad los dos sentidos, el convencional y el electrónico. Es claro que si se invierte el sentido de la corriente, se invertirá el sentido de giro de las líneas de fuerza magnéticas. Obsérvese que el flujo magnético producido por una corriente eléctrica rectilínea carece de polos. Esto hace que la fuerza producida por ese campo magnético sea de difícil aplicación práctica. Una solución a este problema consiste en arrollar el conductor alrededor de un cilindro. De esta manera se construye una bobina o solenoide, figura 6.2.6. De paso aclaremos que al cilindro se le llama forma de la bobina. I Figura 6.2.6 El primer efecto que se consigue es aumentar la densidad de flujo magnético, pues ahora la misma corriente, al pasar repetidamente alrededor del cilindro multiplica su efecto magnético. El flujo magnético resultante será proporcional a la fuerza magneto motriz que se puede calcular de la siguiente manera: FMM = I× N Ing. Aldo Lugli Tancredi 6.3 53 EMBA Apuntes EB- Corriente continua Donde FMM es la fuerza magneto motriz, que se mide en ampervuelta, I es la intensidad de corriente y N es el número de vueltas (o espiras) de la bobina. El segundo efecto importante es el de generar un campo magnético cuyas líneas de fuerza se parecen mucho a las de una barra de imán, ahora con polos en los que se concentran las líneas de fuerza haciendo al dispositivo de gran aplicación técnica. Veamos como se logra esto. Supongamos que a la bobina de la figura 6.2.6 la cortamos mediante un plano paralelo a la hoja de papel y que pasa por el eje del cilindro. En la figura 6.2.7 podemos observar el corte de los conductores. En los de arriba la corriente entra mientras que en los de abajo la corriente sale. La corriente fue de arriba hacia abajo por detrás del papel. Figura 6.2.7 Si ahora dibujamos las líneas de fuerza, aplicando la regla del tirabuzón, resultarán círculos concéntricos alrededor de cada conductor. Veámoslo con más detalle en la figura 6.2.8, que nos muestra lo que sucede entre dos conductores de espiras consecutivas. Figura 6.2.8 Véase que las fuerzas producidas entre los conductores son iguales (ya que la corriente es la misma en ambos) y opuestas, por lo que se anulan. Se generan entonces líneas de fuerza que abrazan a ambos conductores, figura 6.2.9. 54 Ing. Aldo Lugli Tancredi EMBA Apuntes EB- Corriente continua Figura 6.2.9 La bobina presentará, entonces, un campo de forma similar al de una barra de imán, pero con la ventaja que la densidad de flujo y el sentido de la fuerza aplicada dependerán de la intensidad y sentido de la corriente. Esto lo hace muy útil pues es un imán controlable o ajustable. Puede decirse, sin temor de cometer una exageración, que todo el desarrollo tecnológico actual, en cualquier campo de la técnica es posible gracias al campo magnético generado por una corriente eléctrica. Motores, parlantes, discos rígidos, transformadores, por nombrar solo algunos dispositivos que basan su funcionamiento en estos campos magnéticos. La figura 6.2.10 nos muestra el campo formado por una bobina. Figura 6.2.10 La corriente eléctrica tiene otros efectos muy importantes como por ejemplo los químicos. Los efectos brevemente reseñados son los más importantes desde el punto de vista de las aplicaciones referidas al sonido. Ing. Aldo Lugli Tancredi 55