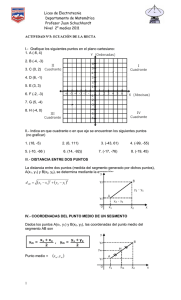
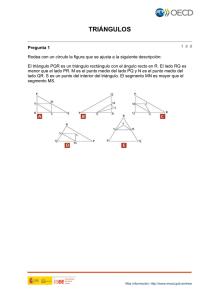
Guía Proporcionalidad de segmentos
Anuncio
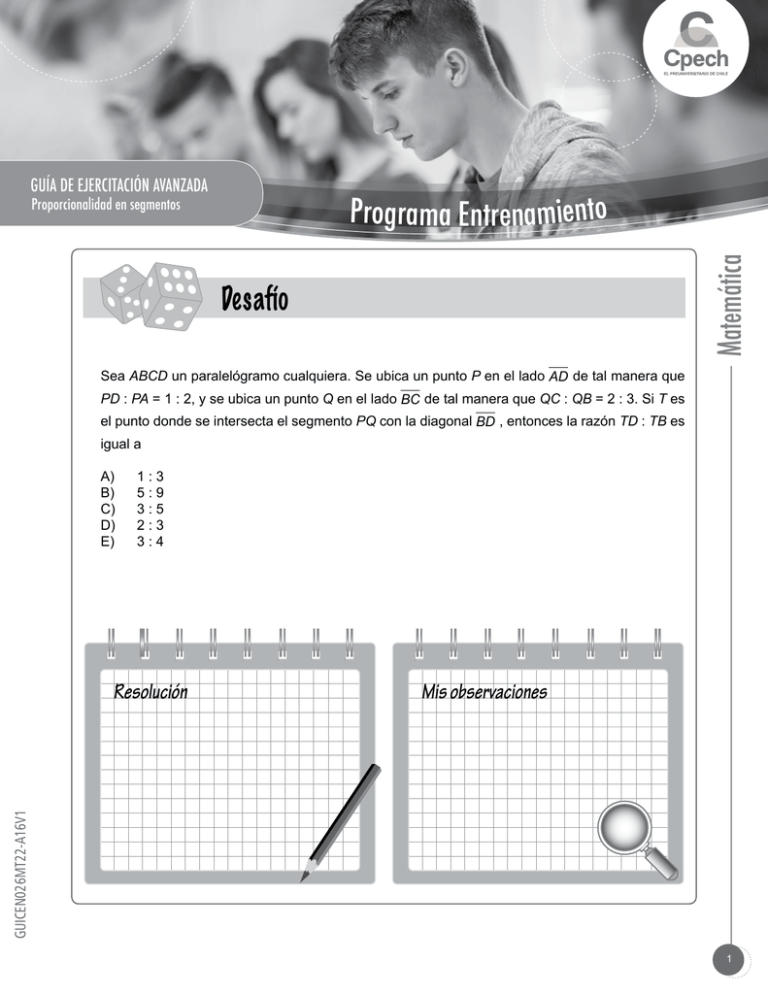
GUÍA DE EJERCITACIÓN AVANZADA Matemática Programa Entrenamiento Proporcionalidad en segmentos Desafío Sea ABCD un paralelógramo cualquiera. Se ubica un punto P en el lado AD de tal manera que PD : PA = 1 : 2, y se ubica un punto Q en el lado BC de tal manera que QC : QB = 2 : 3. Si T es el punto donde se intersecta el segmento PQ con la diagonal BD , entonces la razón TD : TB es igual a A) B) C) D) E) 1:3 5:9 3:5 2:3 3:4 Mis observaciones GUICEN026MT22-A16V1 Resolución 1 Programa Entrenamiento - Matemática Marco teórico División de segmento Existen varios tipos de división de segmento: A P B A B P A P B El punto P divide interiormente al segmento AB en la razón m : n si El punto P divide exteriormente al segmento AB en la razón m : n si El punto P divide en sección áurea o divina al segmento AB si m AP = n PB m AP = n BP AB PB = = ϕ , con PB > AP PB AP Si dos puntos dividen a un segmento, uno interiormente y otro exteriormente en la misma razón, se dice que lo dividen “armónicamente”. 2 División en sección áurea o divina División exterior División interior El número ϕ es una constante llamada el “número dorado” ϕ= 1+ �5 2 ≈ 1,618... GUÍA DE EJERCITACIÓN AVANZADA Teorema de la bisectriz A aa Un segmento de bisectriz dentro de un triángulo determina trazos proporcionales a los lados. B D C AB Si AD es bisectriz del ángulo BAC, entonces… BD = AC DC Teorema de Thales Rectas paralelas determinan segmentos proporcionales AB BD = AC AB CE BC A D C BC // DE DE AC EF CE A L1 L2 B = L3 C A D BC CD B E B = C F D E L1 // L2 // L3 AB BC = E AB // DE AD AC DE AB = CE DE Como Δ ABC ~ Δ ADE, entonces… Como Δ ABC ~ Δ EDC, entonces… AC BC = AE BC DE AB = CD DE 3 Programa Entrenamiento - Matemática Homotecia Es una transformación geométrica que afecta a longitudes en función de una determinada razón k y un punto fijo O llamado centro de homotecia. El triángulo ABC se transforma en el triángulo DEF Si k < − 1 Si k = – 1 C A O E F Si − 1 < k < 0 Si 0 < k < 1 C D D E A A B C B D O F 4 D O F E F Todas las longitudes se multiplican por 1, es decir, las distancias son iguales en relación al triángulo ABC. B C E Todas las longitudes se multiplican por |k| y son mayores en relación al triángulo ABC. F C A O E B B O Si 1 < k Todas las longitudes se multiplican por |k| y son menores en relación al triángulo ABC. D A Todas las longitudes se multiplican por |k| y son menores en relación al triángulo ABC. Todas las longitudes se multiplican por |k| y son mayores en relación al triángulo ABC. GUÍA DE EJERCITACIÓN AVANZADA Ejercicios PSU 1. Dos segmentos están en la razón 1 : 3. ¿En qué razón quedarán si el segmento mayor es reducido a la mitad? A) B) C) D) E) 2. El segmento AB se divide interiormente en la razón 2 : 3 : 4. Si el segmento menor mide 18 cm, ¿cuánto mide el segmento AB? A) B) C) D) E) 3. ¿Cuál(es) de los siguientes segmentos PQ está(n) dividido(s) interiormente por el punto R en la razón 2 : 5? 1:1 1:3 2:3 3:2 Ninguna de las razones anteriores. 9 cm 27 cm 36 cm 81 cm Faltan datos para determinarlo. 5 I) P II) P 10 R A) B) C) D) E) Q 25 R Q 14 III) P 2 4 R Q Solo I Solo II Solo I y III Solo II y III I, II y III 5 Programa Entrenamiento - Matemática 4. En la figura, S es punto medio de PQ y el segmento RS triplica al segmento PR. El segmento PR es al segmento RQ como A) 1 : 8 P R S Q B) 1 : 7 C) 1 : 6 D) 1 : 4 E) 1 : 3 5. En la figura, AP = 10 cm y PQ = 30 cm. Se ubica un punto B en el segmento PQ, de tal manera que P y Q dividen armónicamente al segmento AB. La medida de BQ es A) B) C) D) E) 6 cm 10 cm 16 cm 20 cm 24 cm 6. En la figura, el punto B divide al segmento AC en la misma razón que el punto C divide al segmento A Q P BD. Si AD = 19 cm, BC = 6 cm y AB > CD, entonces ¿cuánto mide BD ? A) B) C) D) E) 4 cm 9 cm 10 cm 12 cm 15 cm 7. En el triángulo ABC de la figura, BD es bisectriz del ángulo CBA. Si AC = 10 cm, entonces el segmento AD mide A B C C 20 A) cm 7 50 B) cm 11 60 C) cm 11 50 D) cm 7 6 E) ninguna de las medidas anteriores. D 5 cm D A 6 cm B GUÍA DE EJERCITACIÓN AVANZADA 8. En el triángulo ABC de la figura, AD es bisectriz del ángulo BAC. Si BC = p + 1, con p número positivo menor que 2, entonces el segmento BD es igual a C 2p A) 2p + 1 2p B) p+1 2p p C) p+1 p+1 D) 2p + 1 p+1 E) 2p 9. D A B 1 En el triángulo ABC de la figura, el valor de AE es C 9 A) 5 45° 15 B) 7 3 45° 4 5 C) 2 A 16 D) 5 B E 20 E) 7 10. En el triángulo ABC de la figura, AD = x, AB = z y BC = y. El segmento AC es igual a C A) xy z 25º z–x B) xy x(z – x) C) y A 60º D 70º B D)xy x–z E)xy z–x 7 Programa Entrenamiento - Matemática 11. En la figura, E es el punto de intersección entre BC y AD . Si AB // CD, ¿cuál es el valor de AE? D B A)45 B)35 C)25 D)20 E) 5 30 E 10 15 A C 12. En el triángulo AFH de la figura, AB = BC = CD = DE = EF = 2 cm y EG = 3 cm. ¿Cuánto mide AH ? A) 5,3 cm B) 6,6 cm C) 9 cm D) 12 cm E) 15 cm H G A B D C F E 13. En el triángulo ABC de la figura, ED // CB. Si DB = (x + 6) metros y AB = (3x + 6) metros, entonces la medida de AD es A) B) C) D) E) C 1 metro. 2 metros. 4 metros. 8 metros. 12 metros. E 4m A D 12 m B 14. Un poste perpendicular al suelo que mide 2,5 metros proyecta una sombra de 5 metros de largo. Si a esa misma hora y en ese mismo lugar, una casa proyecta una sombra de 9 metros, ¿cuál es la altura de la casa? 8 A) B) C) D) E) 4,5 metros 5,5 metros 6,5 metros 7,5 metros 18 metros GUÍA DE EJERCITACIÓN AVANZADA 15. En la figura, el triángulo PQR es isósceles en R, RP // TM, RQ // TN , PM = 2 y TS = 3. Si PM : MS = 1 : 2, entonces ¿cuál es el valor de RP ? A) 7,5 B) 2,5 R T 3�10 C) 4 P M �10 D) 2 E) S Q N Faltan datos para determinarlo. 16. Un edificio que proyecta una sombra de 15 metros, está a 5 metros de otro edificio de 12 metros de altura, tal como muestra la figura. ¿Cuál es el valor de x? A) B) C) D) E) 6 metros 8,3 metros 12,5 metros 15 metros 18 metros x 12 m a 5m 15 m 17. En el triángulo de la figura, x es igual a m A) n+m B) m–n m C) n m–n D) m m–n E) m 1 x b n b ninguna de las expresiones anteriores. 9 Programa Entrenamiento - Matemática 18. ¿En cuál(es) de las siguientes figuras el valor de x es 8? I) L4 II) L3 L5 L1 12 14 L2 x 10 L3 L1 // L2 // L3 L4 y L5 son tranversales A) B) C) D) E) L1 L2 III) L4 L1 15 x A) B) C) D) E) L4 x 12 20 15 5 6 L2 L1 // L2 L1 // L2 L3 y L4 son tranversales L3 y L4 son tranversales Solo en I Solo en II Solo en III Solo en I y en II En ninguna de ellas. 19. En la figura, AB // CD . Si 2 • DE = AD, entonces ¿cuál es el valor de L3 CD ? 2 10 B 3 4 5 6 Ninguno de los valores anteriores. 25º A 8 55º E 12 D C 20. En el triángulo PQR de la figura, RS : SP = 1 : 2. ¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s)? I) PQ RS = RP ST II) RT 1 = TQ 2 III) RP TQ = SP RQ A) B) C) D) E) Solo II Solo I y II Solo I y III Solo II y III Ninguna de ellas. 10 R S P a a T Q GUÍA DE EJERCITACIÓN AVANZADA 21. En el triángulo ABC de la figura, DE // BC . Si AD = (x + 4), DB = (x + 6), AE = x y EC = (x + 1), entonces ¿cuál es el valor de AE? C A)4 B)3 C)2 D)1 E) Ninguno de los valores anteriores. E A B D 22. En la figura, AB // CD y AD se intersecta con BC en E. La expresión que representa a AD en función de p, q y r es B pr A) q D p qr B) p r qr C) + r p A E q C rp D) + r q E) ninguna de las expresiones anteriores. 23. En el triángulo ABE de la figura, AB // CD. Si AB = 3b, AC = 3a y CE = a, entonces CD es igual a E 3 A) b 4 3 B) ab 4 4 C) ab 3 C A D B D) a E) faltan datos para determinarlo. 11 Programa Entrenamiento - Matemática 24. En la figura se muestra una homotecia de centro O que transforma al triángulo ABC en el triángulo DEF. Si OC > OF, ¿cuál de las siguientes afirmaciones es correcta respecto a la razón de homotecia? C D E O B F A) B) C) D) E) A Es menor que – 1. Es igual a – 1. Es mayor que – 1 y menor que 0. Es mayor que 0 y menor que 1. Es mayor que 1. 25. En la imagen, O es centro de homotecia que transforma al cuadrilátero ABCD en el cuadrilátero EFGH, con una razón de homotecia igual a 1,5. ¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s)? I)Si EF = 18, entonces AB = 12. II) Si el perímetro de ABCD es 44, entonces el perímetro de EFGH es 66. III)Si OA = 18, entonces AE = 27. A) B) C) D) E) Solo I Solo I y II Solo I y III Solo II y III I, II y III O C D B G A H E 12 F GUÍA DE EJERCITACIÓN AVANZADA 26. En la figura se muestra una homotecia de centro O y razón – 2,5 que transforma al triángulo ABC en el triángulo DEF. Si ∠ ABC = 60º y BC = 8, ¿cuál es la medida del segmento FG? F B D E O A G C A) 10�3 B) 10�2 C) 8�3 5 D) 20�2 E) 20�3 27. En la figura, AB = 26 cm. Se puede determinar la medida del segmento AD si: (1) AD : DB = 6 : 7 DB es el segmento mayor. (2) A)(1) por sí sola. B) (2) por sí sola. C) Ambas juntas, (1) y (2). D) Cada una por sí sola, (1) ó (2). E) Se requiere información adicional. A D B 28. En la figura, AD y BC se intersectan en E. Se puede determinar la medida de BE si: A) B) C) D) E) (1) por sí sola. (2) por sí sola. Ambas juntas, (1) y (2). Cada una por sí sola, (1) ó (2). Se requiere información adicional. D B (1) AB = 10 cm y EC = 6 cm (2) EC = 6 cm y ED = 4 cm a E 8 cm a A C 13 Programa Entrenamiento - Matemática 29. En el triángulo ABC de la figura, se puede determinar el valor numérico de DE si: C AB // DE y CD = 8 (1) (2) AB = 21 y AD = 12 A) B) C) D) E) (1) por sí sola. (2) por sí sola. Ambas juntas, (1) y (2). Cada una por sí sola, (1) ó (2). Se requiere información adicional. D E A B 30. En la figura, L4 y L5 son transversales, L1 // L2 // L3 y DE = 2. Se puede determinar el valor de EF si: (1) (2) 14 A) B) C) D) E) AD 3 = BE 4 L4 L1 AB 3 = BC 4 (1) por sí sola. (2) por sí sola. Ambas juntas, (1) y (2). Cada una por sí sola, (1) ó (2). Se requiere información adicional. L2 L3 C B A L5 D E F GUÍA DE EJERCITACIÓN AVANZADA Tabla de corrección Item Alternativa Habilidad 1 Aplicación 2 Aplicación 3 ASE 4 Aplicación 5 Aplicación 6 Aplicación 7 Aplicación 8 Aplicación 9 Aplicación 10 Aplicación 11 Aplicación 12 Aplicación 13 Aplicación 14 ASE 15 ASE 16 Aplicación 17 Aplicación 18 Aplicación 19 Aplicación 20 Comprensión 21 Aplicación 22 Aplicación 23 Aplicación 24 Comprensión 25 ASE 26 Aplicación 27 ASE 28 ASE 29 ASE 30 ASE 15 Registro de propiedad intelectual de Cpech. Prohibida su reproducción total o parcial.