DISTRIBUCIÓN DEGENERADA

DISTRIBUCIÓN DEGENERADA O CASUAL.
Una v. a. u. X (variable aleatoria unidimensional) decimos que es
DEGENERADA o CASUAL en un punto c Î ¡ (X ∼ Degenerada(c)) cuando su
función de masa o probabilidad viene dada por la función:
PX (X = x ) = fX (x ) = 0 × I {¡—c} (x ) + 1 × I c (x ) ;
{ }
Donde:
 1 si x ∈ c
I{ A} ( x ) = 
 0 si x ∉ c
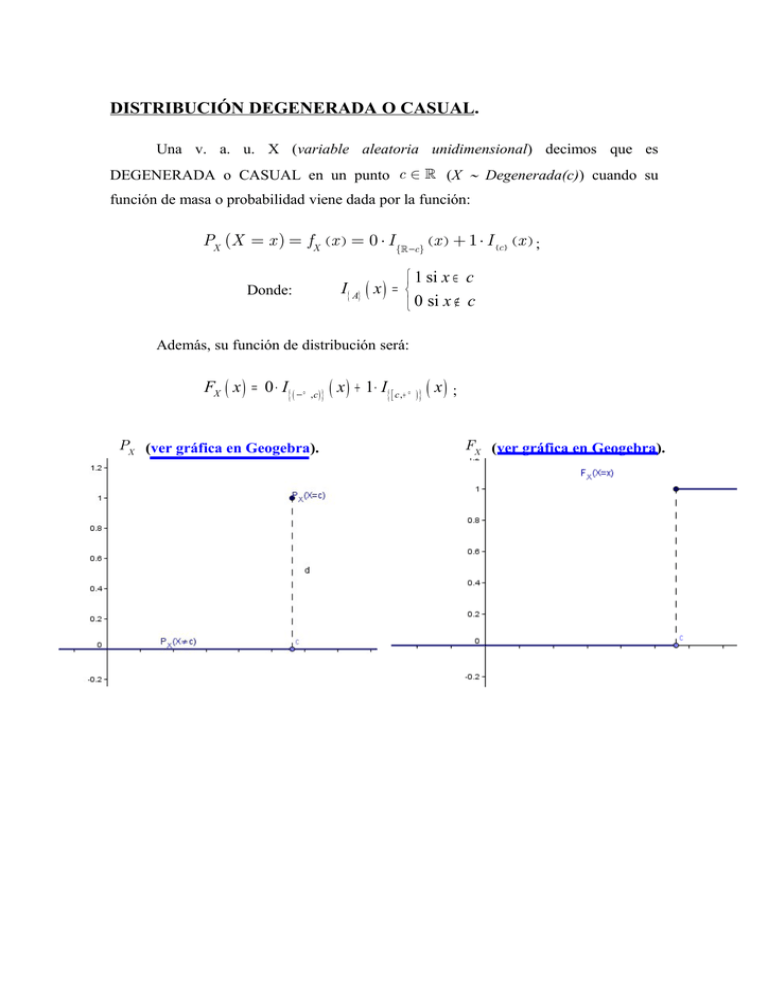
Además, su función de distribución será:
FX ( x ) = 0 ⋅ I{ ( — ∞ ,c ) } ( x ) + 1⋅ I{ [ c ,+ ∞ ) } ( x ) ;
PX (ver gráfica en Geogebra).
FX (ver gráfica en Geogebra).
Algunos parámetros característicos son (ver parámetros característicos en Excel):
MEDIDAS DE CENTRALIZACIÓN O DE POSICIÓN.
MOMENTO DE ORDEN
kΥ
α k = E { X k } = c k ⋅ PX ( X = c ) = c k
MOMENTO ABSOLUTO DE ORDEN
α
k
{ }=
= E X
k
kΥ
c ⋅ PX ( X = c ) = c
k
k
MEDIA
α = α 1 = E{ X} = c
MEDIA GEOMÉTRICA
e
LOG ( c ) ⋅ PX ( X = c )
= c1 = c; Si c > 0
 e
= 
Si c ≤ 0
 No existe
E{ LOG ( X ) }
MEDIA ARMÓNICA
( E{ X} )
−1
MODA = M d
1
si c ≠ 0
1

=
= c
( E { X } )  No existe si c = 0
=c
MEDIDAS DE DISPERSIÓN.
MOMENTOS RESPECTO DE LA MEDIA DE ORDEN k Î ¥
µk = E
{ ( X − α ) } = ( c − c)
k
k
⋅ PX ( X = c ) = 0
MOMENTOS ABSOLUTOS RESPECTO DE LA MEDIA DE ORDEN
µ
k
{
= E X−α
k
}=
kΥ
c − c ⋅ PX ( X = c ) = 0
k
VARIANZA
Var ( X ) = µ 2 = 0
DESVIACIÓN TÍPICA
σ ( X) =
Var ( X ) = 0
DESVIACIÓN ABSOLUTA RESPECTO DE LA MEDIA ARITMÉTICA
Dα = E { x − α
}=
µ1 = 0
COEFICIENTE DE VARIACIÓN DE PEARSON
C.V . =
σ ( X)
α
OTRAS MEDIDAS.
FUNCIÓN GENERATRIZ
G (s ) = E {s X } = s c .PX (X = c ) = s c ;
sΡ
FUNCIÓN GENERATRIZ DE MOMENTOS
M ( θ ) = E { eθ . X } = eθ .c .P ( X = c ) = eθ .c ; θ ∈ ¡
FUNCIÓN CARACTERÍSTICA
f (t ) = E {e X .t .i } = e c .t .i .P (X = c ) = ec .t .i ;
$
$
$
tΡ