Impulso y cantidad de movimiento
Anuncio

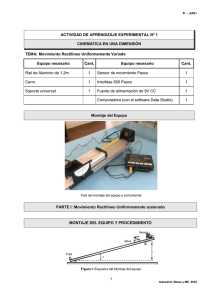
Instituto de Profesores “Artigas” 6 Física Experimental 1 Guía práctica Nº5 r r Impulso ( J ) y cantidad de movimiento ( p ): Colisiones. En una colisión, sobre cada partícula que interviene en la misma, una fuerza relativamente grande actúa durante un tiempo relativamente corto. La idea básica de colisión consiste en que el movimiento de las partículas que colisionan (o al menos de una de ellas) cambia de manera brusca, y que podemos hacer una separación relativamente clara de los tiempos de “antes de la colisión” y de los de “después de la colisión”. Cuando un jugador de fútbol golpea la pelota, el comienzo y el final de la colisión pueden determinarse con bastante precisión. El F(N) pie está en contacto con la pelota durante un intervalo bastante corto en comparación con el tiempo durante el cual observamos la pelota. Durante la colisión el pie ejerce una fuerza t f r grande sobre la pelota. Esta fuerza varía con el F . dt t(s) ti tiempo de modo complejo, tal como muestra la gráfica. ∫ ti tf Las fuerzas que actúan durante un tiempo corto en comparación con el tiempo de observación del sistema se denominan fuerzas impulsivas. A partir de la segunda ley de Newton: r dpr F= dt 1 r r ⇒ F .dt = dp e integrando, ∫ tf ti r pf r tf r r r F .dt = ∫ dp ⇒ ∫ F .dt = p f − pi pi ti r La expresión que aparece a la izquierda de la igualdad se conoce como Impulso J de la r fuerza, y se obtiene como el área bajo el gráfico F= f(t), mientras que p se conoce como cantidad de movimiento 1 2 En mecánica clásica, esta expresión es equivalente a r p del cuerpo. r r F = m.a para una sola partícula. En la teoría de la relatividad, ya no es válida la segunda ley expresada de esta segunda forma. Sin embargo resulta que la forma cantidad de movimiento de una partícula se define como: m= m0 r m0 .v r p= v2 1− 2 c r dpr de la segunda ley sigue siendo válida si la F= dt . Este resultado sugiere una nueva definición de masa: . En esta ecuación v es la velocidad de la partícula, c la velocidad de la luz y m0 es la “masa en reposo” del cuerpo (su masa v2 1− 2 c cuando v=0). De esta definición podemos esperar que la masa de la partícula aumente conforme lo haga su rapidez. Este concepto puede comprobarse con partícula elementales como protones y electrones ya que pueden alcanzar velocidades enormes comparables con la de la luz. Los resultados de dichos experimentos indican que este efecto es real y está determinado en forma exacta por la ecuación anterior. 2 Esta magnitud también se conoce como ímpetu, momento lineal, o momento. r r Para un cuerpo de masa constante m, p = m.v y la expresión anterior puede escribirse como: ∫ tf ti r r r F .dt = m.v f − m.vi . La ecuación anterior es el enunciado matemático del teorema impulso-cantidad de movimiento: r El impulso ( J ) de la fuerza neta que actúa sobre una partícula durante un intervalo de tiempo determinado es igual a la variación en la cantidad de movimiento r ( Δp ) de la partícula durante ese intervalo. Verificaremos el teorema impulsocantidad de movimiento haciendo chocar el carro de un riel de aire contra un sensor de fuerza conectado a la interface LabPro de Vernier. El riel de aire consiste en un perfil de aluminio con gran número de perforaciones por las que sale aire a presión, logrando que el carro levite y pueda deslizar sin rozar contra el mismo. En la figura de la izquierda se muestra un riel de aire de la firma Leybold que utilizaremos, con accesorios. Interface de adquisición de datos. Conocemos como interface analógico-digital a un dispositivo electrónico que, comandado por un software, permite realizar medidas del mundo físico para almacenarlas y procesarlas en un PC. El dispositivo, básicamente, registra valores de voltaje en función del tiempo. Se basa en una electrónica conocida como conversor analógico-digital (ADC, por su sigla en inglés) el cual traduce un valor de voltaje en un dato (número en binario) que el PC es capaz de manejar. La figura de la izquierda muestra la interface LabPro de la firma Vernier, que utilizaremos en este práctico. El programa de comando (Windows) es el Logger Pro. 3 Si deseamos medir diversas magnitudes físicas con la interface, debemos conectarle a sus entradas los sensores correspondientes. Un sensor es un dispositivo que convierte la magnitud física a medir (por ejemplo: fuerza, presión, temperatura, intensidad luminosa, etc.) en un voltaje, para que luego éste último sea manejado por la interface. En la figura de la derecha se muestra el sensor Dual-Range Force Sensor que utilizaremos en el práctico. 3 En los laboratorios de los Liceos de Enseñanza Secundaria puede encontrarse la interface CASSY de la firma Leybold, con varios programas (DOS) de comando, como el “Medir y evaluar”. En el laboratorio de Física del IPA contamos también con la interface Multilog, con su programa (Windows) Multilab. Los sensores se construyen en base a transductores, elementos que convierten cierta magnitud física en un voltaje; por ejemplo: 1. un LDR (resistor dependiente de la luz) intensidad luminosa en voltaje, 2. un termistor, temperatura en voltaje, 3. un sensor Hall, intensidad de campo magnético en voltaje. Para la obtención y acondicionamiento de estas señales a la salida del transductor eventualmente podrán necesitarse fuentes de alimentación y filtros que pueden estar incluidas en el sensor o en una “caja de sensor” dependiendo del modelo de interface disponible. De esta forma tenemos una herramienta de registro y análisis muy poderosa en el laboratorio, ideal para utilizarse cuando, por ejemplo, necesitamos registrar magnitudes que varíen muy rápidamente en el tiempo. Las interfaces se caracterizan, básicamente, por lo siguiente: 1. precisión de conversión: que depende de la resolución del ADC, y se expresa por el número de bits. 2. frecuencia de muestreo máxima: que refiere a la frecuencia máxima a la cual puede registrar voltajes. En general se expresa en muestras por segundo 4 . 3. rangos admisibles: referido a los valores extremos de voltaje que soporta en sus entradas. 4. número de canales: refiere al número máximo de entradas que puede leer simultáneamente 5 . ¿Qué frecuencia de muestreo utilizar? Cuando trabajamos con señales periódicas y deseamos determinar la frecuencia o frecuencias presentes en la misma, el criterio de Nyquist provee una base para obtener la repuesta. El criterio establece que, para determinar sin ambigüedades la frecuencia de una señal, la frecuencia o tasa de muestreo debe ser, por lo menos, dos veces mayor que la máxima componente de frecuencia presente en la señal original. ¿Qué sucederá si se trabaja con un valor menor de frecuencia de muestreo? Cuando la señal sea reconstruida exhibirá un fenómeno llamado aliasing, que se manifiesta por la presencia de componentes de frecuencias espurias en la señal reconstruida. Estas no se encuentran en realidad presentes en la señal original, sino que son el resultado de una adquisición incorrecta. A causa de este fenómeno de aliasing pueden perderse totalmente algunas de las componentes de frecuencia de la señal original Montaje del dispositivo experimental: 1. Riel de aire 2. Carro 3. Fleje 4. Vástago 5. Sensor de fuerza 6. “Bumper” 7. Varilla (Por claridad se omiten las barreras ópticas) 4 5 7 2 4 5 3 6 1 Esta frecuencia estará limitada por el tipo de sensor que conectemos a la interface. El número de canales utilizados a la vez limita la frecuencia máxima de muestreo. Procedimiento: Verifique que dispone de los componentes de la figura, fuente de aire para el riel, cronómetro digital y 2 barreras ópticas, balanza, interface LabPro (Vernier), PC y cables de conexión. Monte los componentes, encienda la fuente de aire y regule el flujo de salida hasta que el carro(2) quede suspendido sobre el riel(1). Nivele el riel mediante los tornillos en su base, de forma que el carro se mantenga en reposo en un plano horizontal. Realice los ajustes necesarios para que el vástago(4) fijo al carro pueda interrumpir las barreras ópticas. Verifique que el sensor de fuerza Dual-Range Force Sensor (5) esté configurado para ±10N (resolución: 0.01N) y que el “bumper”(6) esté alineado con el eje de simetría del carro, que pasa por el punto donde está fijo el fleje(3). Mida la distancia ∆x entre los sensores de las barreras luminosas. Determine la masa del carro. Ejecute el programa “LoggerPro 3.3”, que comanda la interface. Se abre una ventana general que contiene un cuadro de datos tiempo-fuerza, el gráfico F= f(t). Debe configurar la frecuencia de muestreo a 1000 muestras por segundo (máxima para el sensor utilizado). Ponga en cronómetro digital en cero y encienda el aire. Haga clic en el botón “zero” y luego “collect”, con lo cual comienza la medición. Impulse, con cuidado, el carro hacia el sensor de fuerza, registrando el intervalo de tiempo de ida ∆ti y total ∆t(i+f) en el cronómetro digital. Una vez obtenida la gráfica F=f(t) en pantalla, amplíela lo suficiente para discernir claramente los instantes inicial y final de la colisión, seleccione la región correspondiente y seleccione en el programa el cálculo de la integral. Repita varias veces las medidas. Compare los valores de impulso y variación de cantidad de movimiento, considerando las incertidumbres involucradas. Discuta las modificaciones necesarias para minimizar sus valores. Usted supone que las velocidades inicial y final del carro son constantes. Verifique el rango de validez de esta afirmación. Esta guía ha sido escrita, revisada y/o corregida por los profesores del curso de Física Experimental 1, de la especialidad Física, del Instituto de Profesores "Artigas": Guzmán Trinidad, Alejandra Delgado, Gustavo Carbonell y Daniel Baccino. La primera versión fue escrita en 2008. La última revisión se ha hecho en 2010. BIBLIOGRAFIA: Gardner, David, “Physics with Computers”, Experiment #20 “Impulse and Momentum” (Vernier) Gil, S Rodríguez , “Física Re- Creativa”, Ed. Pearson Educación Argentina Halliday, D., Resnick, R., Krane, K., “Física”, Volumen I, Ed. Cecsa, 1992