x - MatesJoseHierroGetafe
Anuncio
Examen de Matemáticas 3º ESO
Nombre:________________
Escribe los resultados en estas hojas. Realiza los ejercicios mostrando los cálculos y los
razonamientos utilizados en la hoja en blanco, precedidos por el número del ejercicio y su apartado.
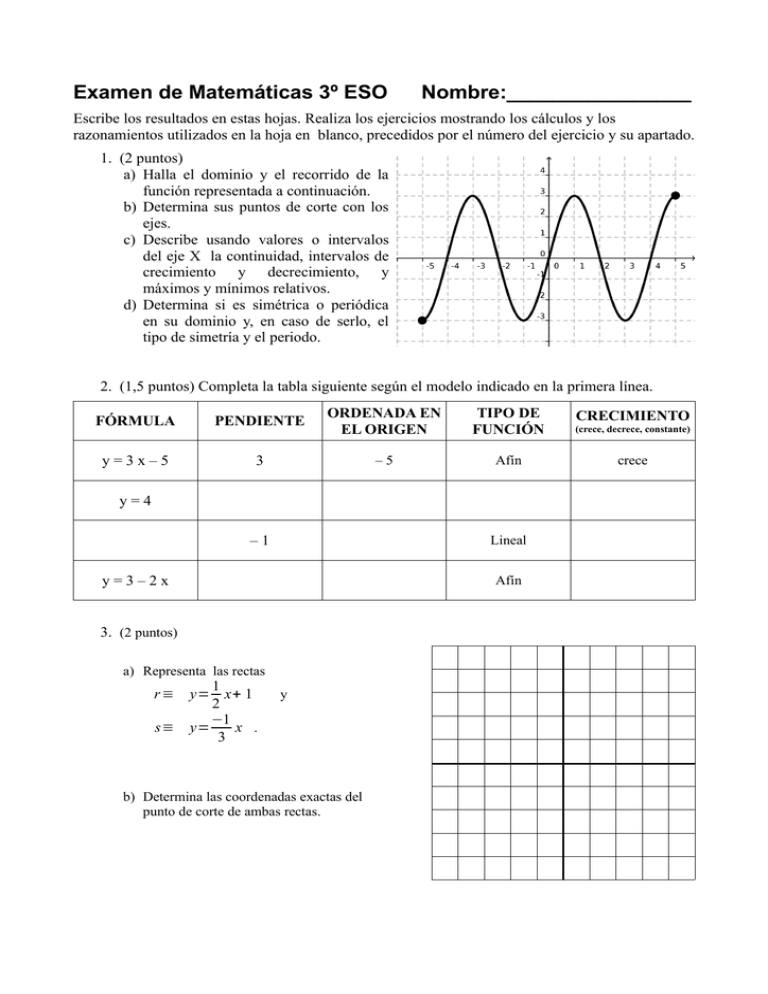
1. (2 puntos)
a) Halla el dominio y el recorrido de la
función representada a continuación.
b) Determina sus puntos de corte con los
ejes.
c) Describe usando valores o intervalos
del eje X la continuidad, intervalos de
crecimiento y decrecimiento, y
máximos y mínimos relativos.
d) Determina si es simétrica o periódica
en su dominio y, en caso de serlo, el
tipo de simetría y el periodo.
2. (1,5 puntos) Completa la tabla siguiente según el modelo indicado en la primera línea.
FÓRMULA
PENDIENTE
ORDENADA EN
EL ORIGEN
TIPO DE
FUNCIÓN
(crece, decrece, constante)
y=3x–5
3
–5
Afín
crece
y=4
–1
Lineal
y=3–2x
Afín
3. (2 puntos)
a) Representa las rectas
r≡
s≡
1
y= x+ 1
2
−1
y=
x .
3
y
b) Determina las coordenadas exactas del
punto de corte de ambas rectas.
CRECIMIENTO
4. (2,5 puntos) PROBLEMA. Pedro tiene al lado de casa dos cibercafés, H y K, para
conectarse a Internet. En el cibercafé H cobran 1,25 € por el enganche a Internet y 0,02 €
por minuto de conexión. En el K no cobran por el enganche, pero cobran 0,03 € por minuto
de conexión.
a) Halla la tabla de las funciones que relacionan el tiempo de conexión (en minutos) con el
coste (en euros) en cada cibercafé.
Tiempo en minutos
0
100
200
Coste de H (euros)
Coste de K (euros)
b) Pedro piensa estar 100 minutos utilizando Internet. ¿Dónde irá para que le salga más
barato?
c) Halla la fórmula de cada una de las funciones.
d) Pedro se da cuenta de que H sale, a la larga, más barato. ¿A partir de qué tiempo de
utilización conviene entrar en H?
5. (2 puntos) PROBLEMA. La tarifa de un parking que permanece abierto desde las 8 de la
mañana hasta las 22 horas, varía según la gráfica.
a) ¿Cuáles son las variables independiente y dependiente y en qué unidades se miden?
b) Halla la ecuación de la recta que indica el precio entre 6 y 10 horas de aparcamiento.
c) ¿Cuánto debe pagar José si deja su coche aparcado 8 horas?
d) Determina el dominio, el recorrido, la continuidad, y los intervalos de crecimiento,
decrecimiento o constancia de la gráfica.
Examen de Matemáticas 3º ESO
Solución
Escribe los resultados en estas hojas. Realiza los ejercicios mostrando los cálculos y los
razonamientos utilizados en la hoja en blanco, precedidos por el número del ejercicio y su apartado.
1.
Rec=[−3, 3] .
a) Dom=[−5, 5]
b) Corte con eje X: x= – 4, x= – 2, x= 0 , x= 2 , x= 4. (También
puede escribirse A=(−4,0) , B =(−2,0) , C=(0,0) , D=( 2,0) , E =(4,0) )
Corte con eje Y: y= 0
(o C=(0,0) )
c) Continua en (−5, 5) ; Discontinua en x= – 5 y x=5
Crece en (−5,−3)∪(−1,1)∪(3,5)
Decrece en (−3,−1)∪(1,3)
Máximos: x= – 3, x= 1, x= 5
Mínimos: x= – 5, x= – 1, x= 3.
d) Es simétrica respecto al origen (es una función impar).
Es periódica en su dominio, con periodo T= 4.
2. (1,5 puntos) Completa la tabla siguiente según el modelo indicado en la primera línea.
FÓRMULA
PENDIENTE
ORDENADA EN
EL ORIGEN
TIPO DE
FUNCIÓN
(crece, decrece, constante)
y=3x–5
3
–5
Afín
crece
y=4
0
4
CONSTANTE
CONSTANTE
y=-x
–1
0
Lineal
DECRECE
y=3–2x
–2
3
Afín
DECRECE
CRECIMIENTO
3. (2 puntos)
a) Representa las rectas
r≡
1
y= x+1 y
2
s≡
y=
x
1
y= x+1
2
x
0
1
0
0
2
2
3
–1
y=
−1
x
3
b) Determina las coordenadas exactas del
punto de corte de ambas rectas.
}
1
y= x+1
1
−1
2
→ x+1=
x →
2
3
−1
y=
x
3
→
}
1
1
5
−6
x+ x=−1 → x=−1→ x=
2
3
6
5
−1 −6 3⋅2 2
y= ⋅ =
=
3 5 3⋅5 5
⇒ P =(−6 /5, 2 /5)=(−1 ' 2, 0 ' 4)
⇒
r
−1
x .
3
s
4. (2,5 puntos) PROBLEMA. Pedro tiene al lado de casa dos cibercafés, H y K, para conectarse a
Internet. En el cibercafé H cobran 1,25 € por el enganche a Internet y 0,02 € por minuto de conexión.
En el K no cobran por el enganche, pero cobran 0,03 € por minuto de conexión.
a) Halla la tabla de las funciones que relacionan el tiempo de conexión (en minutos) con el coste
(en euros) en cada cibercafé.
Tiempo en minutos
0
100
200
Coste de H (euros)
1,25
3,25
5,25
Coste de K (euros)
0
3
6
b) Pedro piensa estar 100 minutos utilizando Internet. ¿Dónde irá para que le salga más barato?
Pedro irá al cibercafé K, donde se ahorrará 25 céntimos.
c) Halla la fórmula de cada una de las funciones. Siendo x=tiempo de conexión en minutos,
H: y = 0,02 x + 1,25
K: y = 0,03 x
y = coste en euros
d) Pedro se da cuenta de que H sale, a la larga, más barato. ¿A partir de qué tiempo de utilización
conviene entrar en H?
y=0,02 x+1,25 → 0,02 x+ 1,25=0,03 x → 1,25=0,01 x → x=125 A partir de 125 minutos conviene H.
y=0,03 x
}
5. (2 puntos) PROBLEMA. La tarifa de un parking que permanece abierto desde las 8 de la mañana
hasta las 22 horas, varía según la gráfica.
a) ¿Cuáles son las variables independiente y dependiente y en qué unidades se miden?
x=tiempo de estacionamiento en horas
y = coste de la tarifa en euros
b) Halla la ecuación de la recta que indica el precio entre 6 y 10 horas de aparcamiento.
}
}
6/4=m→m=3/2
−6=−6 m−n
3
A(6,6)
→6=6
m+
n
y=m x +n →
→ 12 = 10 m + n →
⇒ y= x−3
3
6=6⋅ + n→ n=−3
2
B (10,12)→12=10 m+ n
6 = 4m
2
{
}
c) ¿Cuánto debe pagar José si deja su coche aparcado 8 horas?
3
y= ⋅8−3=12−3=9 Debe pagar 9 euros.
2
d) Determina el dominio, el recorrido, la continuidad, y los intervalos de crecimiento,
decrecimiento o constancia de la gráfica.
Dominio = (0, 14]
Crece en (2, 10)
Recorrido =
(4, 12)∪{14}
No decrece en ningún intervalo.
Es discontinua en x=10 y x= 14.
Es constante en
(0, 2)∪(10,14)







