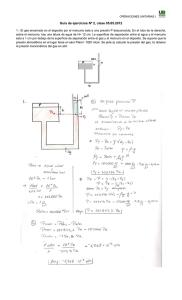
operaciones unitarias ii para ingeniería ambiental informe final de

UNIVERS IDAD NACIONAL DEL CALLAO
FACULTAD DE INGENIERÍA AMBIENTAL Y DE RECURS OS NATURALES
INSTITUTO DE INVESTIGACIÓN
INFORME FINAL DE INVESTIGACIÓN
TÍ TULO :
TEXTO:
OPERACIONES UNITARIAS II
PARA INGENIERÍA AMBIENTAL
I N VES TI GADOR:
Mg . Ing . NAPOLEÓN JÁUREGUI NONGRADOS
(Período de ejecución del 01 de Octubre de 2008 al 30 de Setiembre de 2010, aprobado
con Resolución Rectoral Nº 1165-2008-R)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
2.
ÍNDICE
Pág.
RESUMEN
4
INTRODUCCIÓN
5
MARCO TEORICO
6
MATERIALES Y MÉTODOS
7
RESULTADOS
9
CAPITULO I: ENERGÍA Y CALOR
1.1. Importancia
9
1.2. Estudio
9
1.3. Definición de energía
10
1.4. Balance de energía.
10
1.5. Fundamentos termodinámicos.
12
1.6. Definición del calor
12
1.7. Transferencia de calor.
13
1.8. Tipos de transferencia de calor
13
1.9. Procesos de transferencia de calor
13
CAPITULO II: TRANS FERENCIA DE CALOR POR CONDUCCIÓN
2.1. Importancia
16
2.2. Estudio
16
2.3. Definición de transferencia de calor por conducción
16
2.4. Conducción en superficies planas.
17
2.5. Conducción en superficies cilíndricas.
18
2.6. Conducción en superficies compuestas.
19
CAPITULO III: TRANS FERENCIA DE CALOR POR CONVECCIÓN
3.1. Importancia
27
3.2. Estudio
27
3.3. Definición de transferencia de calor por convección.
27
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
3.
Pág.
3.4. Tipos de transferencia de calor por convección.
28
3.5. Convección forzada.
28
3.6. Convección libre y laminar.
31
3.7. Convección por condensación.
33
CAPÍTULO IV: TRANS FERENCIA DE CALOR POR RADIACIÓN
4.1. Importancia
42
4.2. Estudio
42
4.3. Definición del calor por radiación.
42
4.4. Aplicaciones del calor por radiación
44
4.5. Calor de radiación entre cuerpos.
44
4.6. Calor de radiación perdido en cuerpos planos y cilíndricos.
45
CAPITULO V: INTERCAMBIADORES DE CALOR
5.1. Importancia
48
5.2. Estudio
48
5.3. Intercambiador de calor
49
5.4. Tipos de intercambiadores de calor
49
5.5. Intercambio de calor a Doble Tubo
49
5.6. Intercambiador por Horquillas
52
5.7. Intercambiadores de calor de Tubo y Coraza
57
CAPÍTULO VI: HUMIDIFICACIÓN, S ECADO Y COMBUSTIÓN
6.1. Importancia
70
6.2. Estudio
71
6.3. Humidificación y deshumificación
71
6.4. Secado
77
6.5. Combustión y pasteurización
84
DISCUSIÓN DE RESULTADOS
99
REFERENCIAS BIBLIOGRÁFÍCAS
100
APÉNDICE
101
ANEXOS
102
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
4.
RES UMEN
El presente Texto: Operaciones Unitarias II para Ingeniería Ambiental, estudia los
procesos de transferencia de calor, de tal manera que el Ingeniero Ambiental los
pueda aplicar en diversas operaciones de tratamientos
minimizar los residuos generados en las actividades an
residuos o para
génicos. Asimismo,
tiene como objetivos desarrollar el Texto en forma ordenada y sistemática de
acuerdo al silabo del Plan Curricular de la Facultad de Ingeniería Ambiental y de
Recursos Naturales de la Universidad Nacional del Call
de tal forma que
permita preparar a los alumnos en el análisis de la tr nsferencia de calor, así
como desarrollar en ellos la aptitud y actitud para el
nejo ambiental.
Basados en esta perspectiva, los temas en este texto están desarrollados tanto en
el aspecto teórico y práctico; de tal manera, que permita el fácil entendimiento y
aplicación, siendo su desarrollo también en base a la experienc a docente y en
consulta a material bibliográfico; lográndose obtener
eis capítulos, cuyos títulos
son: energía y calor, transferencia de calor por conducción, transferencia de calor
por convección, transferencia de calor por radiación, intercambiadores
humidificación, secado y combustión.
calor,
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
5.
INTRODUCCIÓN
La Ingeniería Ambiental tiene como herramientas de tra
jo para el manejo
ambiental de las Operaciones Unitarias, que en la especialidad se dividen en
Operaciones Unitarias I y II. Sin embargo, estos temas enfocados a este nivel se
tiene poca información en el campo de la Ingeniería Am
, dado que esta
ingeniería aún es joven. Por tal razón, este Texto: Operaciones Unitarias II para
Ingeniería Ambiental es un instrumento pedagógico que permitirá contribuir en el
logro de las estrategias didácticas del proceso enseña za-aprendizaje, dado que
su contenido favorece el desarrollo de toda malla curr cular de Ingeniería
Ambiental o de ciencias ambientales; fundamentalmente porque los temas so
analizados con aplicación de las ciencias matemáticas, físicas y ambientales.
Por ello, este texto tiene como finalidad cubrir el vacío por la falta de literatura en
el campo ambiental, toda vez, que la Ingeniería Ambiental es una joven
especialidad que nació para hacer frente a la problemática ambiental producido
por el hombre, sobre todo porque siempre pensó en prod cir grandes cantidades,
a bajo costo y en óptima calidad para maximizar utilidades y no le importó trabajar
con calidad ambiental para el logro del desarrollo sos enible. Finalmente, este
texto facilita el proceso enseñanza-aprendizaje del Curso de Operaciones
Unitarias II impartida fundamentalmente en la Facultad
Ingeniería Ambiental y
Recursos Naturales de la Universidad Nacional del Callao. De ahí la importancia
de este texto porque contribuye en la formación de los alumnos de Ingeniería
Ambiental con material acorde a sus necesidades y que
aplicación en el manejo ambiental.
rmite el análisis y la
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
6.
MARCO TEÓRICO
El estudio de la Ingeniería Ambiental en su conjunto no encuentra muchos textos
en que poder documentarse. Si embargo, en estos últimos años han aparecido
algunos textos de Ingeniería Ambiental, el cual motiva a que se tenga mayor
interés en nuevas publicaciones en este campo, sobre t do a nivel especializado,
de manera de poder conocer mejor nuestro sistema y cóm
actuar según la
necesidad; cuyos elementos es un aporte en este texto.
La Ingeniería Ambiental fundamenta su actividad en la aplicación tecnológica de
una producción amigable con el ambiente y para revertir los efectos de dicha
actividad, como son el tratamiento y depuración de efl
es contaminantes, de
tal manera que se logre el manejo ambiental de los rec rsos naturales, teniendo
en cuenta la prevención, conservación y restauración de dichos recursos con
visión holística para el desarrollo sostenible de la h
nidad. Las Operaciones
Unitarias II para Ingeniería Ambiental, tiene los cont nidos para coadyuvar a estos
fines, puesto que basa su estudio en la en la transferencia del calor, dotando a los
alumnos de los instrumentos generales teóricos para que ellos los puedan aplicar
mediante tecnología específica en el tratamiento de materiales de acuerdo a su
tipo de estado (Kiely G., 1999). Además, las Operaciones Unitarias II aplica los
balances másicos y energéticos en los equipos industriales de tal forma que se
optimicen los resultados, para lo cual especifica los tipos de equipos de acuerdo a
las técnicas de separación y de transferencia de masa. Por lo que, las
operaciones unitarias permite la solución de problemas amplios y vastos de la
industria y la manipulación de sus procesos (Foust A., et. al.; 1990).
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
7.
MATERIALES Y MÉTODOS
Teniéndose entendido que el tema de investigación es elaborar un texto, no se
determina el universo de estudio, tampoco técnicas estadísticas.
Se aplicó la siguiente metodología:
ü Formulación del índice del texto.
ü Identificación de la información.
ü Análisis de la información.
ü Redacción del texto en función del índice.
ü Revisión de la redacción y complementación.
ü Presentación del texto.
El texto fue desarrollado en relación al silabo de la
ignatura de Operaciones
Unitarias II de la currícula de estudios de la Faculta de Ingeniería Ambiental y de
Recursos Naturales de la Universidad Nacional del Callao, cuyo desarrollo es en
base a la experiencia docente y con material bibliográfico de apoyo, de manera de
desarrollar seis capítulos, con los siguientes contenidos:
CAPITULO I: ENERGÍA Y CALOR
1.1. Importancia
1.2. Estudio
1.3. Definición de energía
1.4. Balance de energía.
1.5. Fundamentos termodinámicos.
1.6. Definición del calor
1.7. Transferencia de calor.
1.8. Tipos de transferencia de calor
1.9. Procesos de transferencia de calor
CAPITULO II: TRANSFERENCIA DE CALOR POR CONDUCCIÓN
2.1. Importancia
2.2. Estudio
2.3. Definición de transferencia de calor por conducción
2.4. Conducción en superficies planas.
2.5. Conducción en superficies cilíndricas.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
2.6. Conducción en superficies compuestas.
CAPITULO III: TRANSFERENCIA DE CALOR POR CONVECCIÓN
3.1. Importancia
3.2. Estudio
3.3. Definición de transferencia de calor por convección.
3.4. Tipos de transferencia de calor por convección.
3.5. Convección forzada.
3.6. Convección libre y laminar.
3.7. Convección por condensación.
CAPÍTULO IV: TRANSFERENCIA DE CALOR POR RADIACIÓN
4.1. Importancia
4.2. Estudio
4.3. Definición del calor por radiación.
4.4. Aplicaciones del calor por radiación
4.5. Calor de radiación entre cuerpos.
4.6. Calor de radiación perdido en cuerpos planos y ci índricos.
CAPITULO V: INTERCAMBIADORES DE CALOR
5.1. Importancia
5.2. Estudio
5.3. Intercambiador de calor
5.4. Tipos de intercambiadores de calor
5.5. Intercambio de calor a Doble Tubo
5.6. Intercambiador por Horquillas
5.7. Intercambiadores de calor de Tubo y Coraza
CAPÍTULO VI: HUMIDIFICACIÓN, SECADO Y COMBUSTIÓN
6.1. Importancia
6.2. Estudio
6.3. Humidificación y deshumificación
6.4. Secado
6.5. Combustión y pasteurización
8.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
9.
RES ULTADOS
CAPITULO I
ENERGÍA Y CALOR
1.1. Impo rtancia
La importancia de este capítulo para la problemática ambiental, radica en que
introduce los criterios básicos para conocer el calor
su balance energético para
su máximo aprovechamiento, pues la problemática ambiental en gran medida se
debe a la generación de energía en la que el hombre participa directamente y al
no aprovechar correctamente los recursos para su trans ormación en energía
permite que parte de ellos se convierta en elementos r
duales perjudiciales al
ambiente, tal es el caso del vapor de agua que al no darle el uso adecuado
conlleva a que los calderos quemen más combustible y por tanto conlleva al
incremento de gases de efecto invernadero que afecta negativamente nuestro
ambiente. Además este capítulo es importante para la problemática ambiental
porque informa que se debe mantener el sistema en equi rio y ello sólo es
posible si dicho sistema está balanceado, como ejemplo se indica si procesamos
materiales y producto del balance se obtiene diferente al procesado, eso indica
que una parte de lo procesado se ha perdido como resid
; es decir no se ha
optimizado el uso del recurso y en consecuencia estamo contaminando y al
mismo tiempo la empresa está perdiendo dinero por mate
perdido. De este
ejemplo queda claro que el balance de materia es necesario para prevenir
problemas ambientales y económicos.
1.2. Es tudio
En este capítulo, se estudiará la energía y sus transformaciones aplicadas en un
balance de energía, no se estudiará los tipos de energía por no ser materia del
texto. Este estudio por ser parte introductoria se desarrollarán los temas de
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
10.
manera básica los siguientes ítems:
•
Definición de Energía
•
Balance de Energía.
•
Fundamentos termodinámicos.
•
Definición del calor.
•
Transferencia de calor.
•
Tipos de transferencia de calor.
•
Procesos de transferencia de calor.
1.3. De finició n de Ene rgía
Felder (2003), es todo aquello capaz de producir trabajo; también la
ne como
la materia dispersa. Ejemplo de energía: Trabajo, calor, eléctrica, mecánica,
cinético, potencial, solar, eólico, nuclear, etc.
1.4. Balanc e de Ene rgía
El balance de energía cumple el principio de la conservación de la energía o Ley
de Joule, que sostiene “La energía no se crea ni se destruye sólo se transforma”.
Entonces, aplicando este principio a los sistemas cerra
s y abiertos, se cumple:
Energía perdida por un cuerpo = Energía ganada por otro cuerpo
Cuando no existe acumulación de energía en el sistema
umple:
Energía que ingresa = Energía que sale
a) Balance de energ ía en s is tema cerrado
S is tema c errado : Un sistema es cerrado cuando la masa no atraviesa los límites
del sistema durante el periodo del balance de energía, ejemplo de un sistema
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
11.
cerrado es el sistema intermitente. En consecuencia el balance de energía para
este sistema, demostrado por Felder et.al. (2003) es el siguiente:
Energía neta transferida = Energía final – Energía inicial
Resultando:
Q + W = ?U + ?Ec + ?Ep
(1.1)
Esta ecuación es producto del desequilibrio del sistema y es compensado por la
variabilidad de la energía interna, cinética y potencial.
De donde:
Q
= Flujo calorífico transferido.
W
= Trabajo realizado en
sistema.
?U = Variación de la energía interna.
?Ec = Variación de la energía cinética.
?Ep = Variación de la energía potencial.
b) Balance de energ ía en s is tema abierto
S is tema abierto : Un sistema es abierto cuando la masa atraviesa los límites del
sistema durante el periodo del balance de energía, ejemplo de un sistema abierto
es el sistema continuo. En consecuencia el balance de energía para este sistema,
demostrado por Himmelblau (1998) es el siguiente:
Energía neta transferida = Energía final – Energía inicial
Resultando:
Q + Ws = ?H + ?Ec + ?Ep
(1.2)
De donde: Q (Flujo calorífico transferido), Ws (Trabajo realizado en el sistema,
?H
(Variación de la entalpía), ?Ec
(Variación de la energía cinética), ? Ep
(Variación de la energía potencial).
Tanto para balance de energía en sistema abierto y cerrado, a fin de lograr el
balance es necesario primero hacer un diagrama de flujo o de bloques, el cual se
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
debe rotularse; esto significa que el diagrama debe te
12.
r toda la información
como temperaturas, presiones, estados de la materia, etc.
1.5. Fundame nto s term odinámic o s
Bird et.al. (1990), manifiesta que el vapor de agua a nivel industrial es
l más
económico y define esta energía como el ciclo de Rankine, cuyas propiedades
fundamentales termodinámicas de volumen específico, entalpía y entropía se
pueden leer en las Tablas Termodinámicas de Vapor de A ua. Existiendo para
ello dos tipos de tablas, tanto para vapor saturado y ara vapor recalentado, en
ambos casos los datos no leídos se pueden determinar aplicando interpolaciones
sobre los valores más próximos. Para determinar el cal
liberado como producto
de enfriamiento del vapor de agua, se aplica el siguiente modelo termodinámico:
Q = m (h2 – h1)
( 1.3.)
De donde:
Q = Flujo calorífico.
h2 y h1 = Entalpías específicas antes y después del enfriamiento.
m = Flujo másico.
Por lo estudiado, los principios termodinámicos sólo evalúan el inicio y final de
una operación o proceso. Por lo que, la termodinámica valúa los estados del
sistema, esto es el inicio y el final del mismo, toman
en cuenta las propiedades
tales como: presión, temperatura, composición, etc., importando dichas variables
en cada estado alcanzado y no que variaciones tuvieron entre los estados.
1.6. De finició n del Calo r
Himmelblau (1998), define al calor como la parte del flujo total de energía a
través de la frontera de un sistema que se debe a una diferencia de temperatura
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
13.
entre el sistema y su entorno. También afirma que el calor no se crea ni se
almacena.
Asimismo, indicar que el calor es la variable en que se sustenta este texto y al que
se estudiará integralmente su aprovechamiento y las pérdidas a través de
paredes, aportando con diferentes técnicas a fin de poder manejarlo.
1.7. Trans fe re ncia de c alor
El término se utiliza para dar entender tanto energía térmica como transmisión de
energía térmica. La transferencia de calor es la transferencia de energía térmica
producida por una diferencia de temperatura entre un sistema y sus alrededores,
la cual puede o no cambiar la cantidad de energía térmica en el sistema. En la
transferencia de calor, si se evalúa la forma en que el sistema al anzó el estado
final; es decir, se evalúa el sistema antes, durante y después tomando en cuenta
el espacio, tiempo y propiedades; incluso la transfere cia de calor se puede dar
con combinaciones de los tres tipos antes indicados, según el caso que se
presente. Por lo que, el estudio de la transferencia de calor requiere otros
conocimientos con mayor profundidad de análisis de ene
térmica en
comparación al análisis termodinámico.
1.8.
Tipo s de trans fe re nc ia de c alor
Los tipos de transferencia de calor se dan de tres maneras y son los siguientes:
Ø Por conducción
?
Ø Por convección
? El calor que transmite el aire o gases y líquidos.
Ø
? Por cualquier foco de energía.
Por radiación
Roce y contacto entre superficies.
1.9. Pro c e s o s de trans fe re nc ia de c alor
Kern (1999), sostiene que los procesos de transferenc a de calor se relacionan
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
con las razones de intercambio térmico, lo cual es apr
14.
ado en equipos de
transferencia de calor; lo que realza la importancia de las diferencias de
temperatura entre la fuente y el recibidos del calor, lo que es, después de todo, el
potencial por el cual la transferencia de calor se lle
a efecto. Un problema típico
de procesos de transferencia de calor involucra las cantidades de calor que deben
transferirse, las razones a las cuales pueden transferirse debido a la naturaleza
de los cuerpos, la diferencia de potencial, la extensión y arreglo de las superficies
que separan la fuente y el recibidor, y la cantidad de energía mecánica que debe
disiparse para facilitar la transferencia de calor. Pu
to que la transferencia de
calor considera un intercambio en un sistema, la pérdi
de calor por un cuerpo
deberá ser igual al calor absorbido por otro dentro de los confines del mismo
sistema.
Q
Q
A
T1
T2
T1 > T2
Figura Nº 1.1.: Flujo c a lorífic o a travé s de pare de s d un s is te ma.
PROBLEMAS APLICATIVOS
PROBLEMA 1.1.
Durante un proceso de compresión de un ambiente, se realiza sobre el un trabajo
de 20 KJ mientras que el sistema transfiere 13 KJ de calor al medio externo ¿Cuál
es la variación de la energía interna de este medio ambiente?
S OLUCIÓN:
Por modelo de la ecuación (1.1.), se tiene: ?U = Q – W, de aquí Q = - 13 KJ y
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
15.
W = - 20 KJ. Por lo tanto: ?U = 7 KJ
Lo que significa que el ambiente aumenta su energía interna en 7 KJ.
PROBLEMA 1.2.
Para condicionar un ambiente 1000 Kg/h de vapor es descargado sobre el a 1
atm, el cual es mezclado con vapor sobrecalentado de 400 ºC y 1 atm para
producir vapor sobrecalentado de 300 ºC y 1 atm. Si la operación es adiabática
qué cantidad de vapor es producido y qué flujo volumét ico de vapor
sobresaturado se requiere para la mezcla en dicho ambiente.
S OLUCIÓN:
De las tablas termodinámicas, las entalpías del vapor saturado a 1 atm es 2676
kJ/kg y del vapor sobresaturado a mezclar es 3278 kJ/kg y del vapor
sobresaturado producido es 3074 kJ/kg.
Aplicando balance de energía de la ecuación (1.2.), se tiene:
Q + Ws = ?H + ?Ec + ?Ep;
Q = Ws = ?Ec = ?Ep = 0, por ser adiabático y no hay partes móvi
Entonces: n?H = n2H2 + n1H1 - n3 H3 = 0
(a)
De donde: n3 = n2 + n1 , que son los flujos másicos participantes.
Reemplazando valores en la ecuación (a), se tiene:
n3.3074 kJ/kg = n2 .3278 kJ/kg + 1000 kh/h. 2676 kJ/kg
Por lo tanto:
n3 = 2951 kg/h,
que es la cantidad de vapor sobrecalent do
producido por la mezcla.
Hallando el flujo volumétrico del vapor: En tablas termodinámicas a 400 ºC y 1
atm el volumen específico es 3,11 m3 /kg y n1, del cálculo anterior es 1951 kg/h;
por tanto la mezcla en el ambiente requiere: 1951 kg/h . 3,11 m3 /kg = 6070 m3/h.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
16.
CAPITULO II
TRANS FERENCIA DE CALOR POR CONDUCCIÓN
2.1. Impo rtancia
La importancia de este capítulo para la problemática ambiental, radica en que los
procesos por conducción tienen que tenerse presente, dado que toda pared
puede perder calor y en consecuencia si no se toman las medidas de aislamiento
correcto estaremos perdiendo energía alterando aún más la en ropía del sistema
y por tanto la alteración del mismo. Asimismo, es importante porque ilustra todas
las formas de conducción a producirse y de qué manera
s actuar para su
control. Finalmente la transferencia de calor por conducción es importante por ue
ayuda a solucionar la problemática ambiental generada
intercambiantes de calor con el ambiente, al permitirn
las superficies
la elección de materiales
de baja conducción, los cuales se usan como aislantes térmicos.
2.2. Es tudio
Este capítulo basa su estudio en el calor transferido por conducción en la cual
vamos a hacer el estudio en diferentes cuerpos del tipo plano y cilíndrico, en
donde se va a evaluar el comportamiento del calor y cómo este influye cuando
cambia de un cuerpo simple a compuesto o cuando los cuerpos están en serie y
en paralelo o mixto, haciéndose más complejo el estudio pero permite visualizar el
comportamiento del calor en la naturaleza.
2.3. De finició n de trans fe re ncia de c alor por c onduc c ió n
La transferencia de calor por conducción se fundamenta
l calor transferido de
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
17.
un cuerpo a otro que está en contacto y en donde el cu po que pierde calor debe
estar sin movimiento. Kern (2003) indica que este estu
ue hecho por Fourier, y
considerando la Figura 2.1., Fourier determinó la ecuación (2.1.).
La ecuación (2.1.), también se le conoce como ecuación de Fourier y cuyas
variables tienen los siguientes nombres: Q (calor transferido por conducción), k
(conductividad térmica del cuerpo), A (superficie de calefacción), dT (derivada de
la temperatura), dx (derivada del espesor del cuerpo).
?T
Q
A
Q = −k.A
∫ dT
∫ dX
(2.1.)
?X
Figura Nº 2.1. S is te ma c alorífic o
c onduc tivo
Para este estudio se desarrollarán los siguientes ítems:
•
Conducción en superficies planas.
•
Conducción en superficies cilíndricas.
•
Conducción en superficies compuestas.
2.4. Conduc c ión e n s upe rficie s planas
Brown (2003), determinó que en cuerpos planos simples e toma como ejemplo la
Figura 2.2. y aplicando en ella la ecuación de Fourier, esto es la ecuación (2.1.) se
obtiene la ecuación (2.2.).
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
T1
18.
T2
Q
Q = −k . A
A
X1
(T 2 − T 1)
( X 2 − X 1)
(2.2.)
X2
Figura Nº 2.2.: Cue rpo
plano
s imple c onduc tivo
Aplicando a la ecuación (2.2.) variación de temperatura y espesor de la pared, se
obtiene la ecuación (2.3.).
Q=−
∆T
∆X
k .A
Aclarando que: ?T = T2 - T1
(2.3.)
y
?X = X2 - X1
De la ecuación (2.3.) se obtiene la Resistencia Térmica (R), cuya expresión se
muestra en la ecuación (2.4.), entendiéndose como resi
ncia lo que impide el
paso del flujo calorífico.
R=
∆X
k.A
(2.4.)
2.5. Conduc c ión e n s upe rficie s cilíndric as
En cuerpos cilíndricos simples se toma como ejemplo la Figura 2.3. y aplicando
en ella la ecuación de Fourier se obtiene la ecuación 2.5.).
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
19.
L
r2
A
Q = −2p .k .L
r1
∆T
r2
ln
r1
(2.5.)
Q
Figura Nº 2.3.: Cue rpo c ilíndric o s imple c onduc tivo
La ecuación (2.5.), los nombres de sus variables son:
(calor transferido por
conducción), k (conductividad térmica del cuerpo), A (superficie de calefacción), L
(longitud del cilindro o tubo), ?T (variación de la temperatura), r2 y r1 (radio mayor
y menor del cilindro, cuya diferencia determina su espesor); asimismo, en esta
ecuación sólo varían la temperatura y el radio. Por esta razón, son estas últimas
variables los que limitan el valor del calor.
La Resistencia Térmica (R) en cilindros se obtiene a partir de la ecuación (2.5.) y
ordenándola convenientemente, resulta la ecuación (2.6.).
R=
1
r2
ln
2p .k .L r1
(2.6.)
2.6. Conduc c ión e n s upe rficie s c om pue s tas
Para este caso pueden ser en serie o en paralelo.
a) En s uperficies planas en s erie
Considerando dos cuerpos en contacto se obtiene la Fig ra 2.4.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
T1
T2
20.
T3
Q
k1
k2 k2
X1
X2
Figura Nº 2.4.: Cue rpo c ompue s to e n s e rie c onduc tivo
En estos casos como la Figura 2.4. para su estudio es
ecesario formular el
circuito térmico, correspondiendo para este caso la Fi ura 2.5.
R1
T1
T2
^^^^^^^
R2
^^^^^^^
T3
Figura Nº 2.5.: Circ uito té rmic o de la Figura 2.4.
En la conducción en serie se cumple:
R = R1 + R2 + ………+ Rn
(2.7.)
Q = Q1 = Q2 = …….. = Qn
(2.8.)
Es decir la resistencia total (R) es la suma de las re
ncias parciales, en
cambio el calor que pasa a través de los cuerpos es constante.
b) En s uperfic ies planas en paralelo
Considerando dos cuerpos en contacto se obtiene la Figura 2.6. y cuyo circuito
térmico le corresponde la Figura 2.7.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
T1
21.
T2
R1
^^^^^^^
k1
T1
Q
T2
R2
^^^^^^^
k2
K2
Fig ura Nº 2.7.: Circ uito té rmic o
de la Figura 2.6.
X1
Fig ura Nº 2.6.: Cue rpo c ompue s to
c onduc tivo e n parale lo
En la conducción en paralelo se cumple:
Q = Q1 + Q2 + ………+ Qn
(2.9.)
1
1
1
1
=
+
+ ........... +
R R1 R 2
Rn
(2.10.)
Es decir el calor total (Q) es la suma de los calores parciales que pasan a través
de los cuerpos, en cambio la inversa de la resistencia total (R) es la suma de las
inversas de cada resistencia de los cuerpos en paralelo.
c) En s uperficies cilíndricas co mpue s tas
Considerando dos cilindros se obtiene la Figura 2.8.
Aplicando Fourier en la Figura Nº 2.8., se obtiene:
Q=
∆T
R1 + R 2
(2.11.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
22.
Vacío
Cilindro
1
r3
Cilindro
2
r2
r1
Q
Figura Nº 2.8.: Vis ta fro nta l de dos c ilindros
adyac e nte s .
La ecuación 2.11., también se puede expresar con la ecuación 2.12.
Q=
− ∆T
1 1 r2 1 r3
( ln + ln )
2p .L k 1 r1 k 2 r 2
(2.12.)
Entendiéndose que ? T de la ecuación 2.12., es la diferencia térmica de las
superficies de los extremos de la Figura 2.8., es decir, desde el interior al exterior
del mismo.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
23.
PROBLEMAS APLICATIVOS
PROBLEMA 2.1.
Si existe pérdida de calor al medio ambiente, determinar la temperatura T2 por
transferencia de calor según el esquema que se adjunta.
Figura P1-2: Figura del problema 2.1.
S OLUCIÓN:
Conocido las variables de acuerdo al esquema, se determina T2 que es la
temperatura exterior de la pared.
Por tratarse de conducción a través de la pared, se aplica la ley de Fourier:
qcond = qx = q" x. A = − k
dT
T1 − T 2
. A = kA
dx
L
Resolviendo para T2 da:
T 2 = T1 −
qcondL
kA
Sustituyendo los valores numéricos, resulta:
T 2 = 415º C −
3000Wx0,025m
2
0,2W / m.Kx10 m
T2 = 415 ºC - 37,5 ºC
En consecuencia la temperatura hallada es:
T2 = 378 ºC
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
24.
PROBLEMA 2.2.
Del esquema mostrado, hallar el calor perdido al medio ambiente si la pared es de
ladrillo concreto.
Figura P2-2: Figura del problema 2.2.
S OLUCIÓN:
Conocido las variables y por tratarse de conducción donde la pared es función de
las temperaturas que van de -15 a 38 ºC y aplicando la ley de Fourier se tiene:
q" x = − k
dT
T1 − T 2
25º C − ( −15º C )
2
=k
= 1W / m.K
= 133,3W / m
dx
L
0,30m
qx = q" x. A = 133,3W / m .20 m = 2667W
2
Por tanto el calor perdido al ambiente es:
2
PROBLEMA 2.3.
Para evitar afectar al ambiente y tener sobre costo, una empresa tiene dos
alternativas de compra de aislamiento térmico de tipo A y B, ambos disponibles en
planchas de 2 cm de espesor. El aislante A su precio es de 26 Nuevos Soles por
metro cuadrado y del tipo B es de 40 Nuevos Soles por metro cuadrado;
asimismo, las conductividades térmicas son 0,04 y 0,03 Kcal/m.h.ºC de los
materiales A y B respectivamente. Por diseño ambos mat riales son capaces de
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
25.
resistir las temperaturas de 500 y 40 ºC en ambas caras, que son los que van a
soportar producto del trabajo de turnos de 24 horas, con año laboral de 340 días.
También indicar que ambos aislantes tienen una duración de 15 años y el costo
del calor expresado en millón de kilocalorías es de 32 Nuevos Soles. Entonces
qué material decide comprar la empresa para fines de rentabilidad
en beneficio
del ambiente.
S OLUCIÓN:
Evaluando el aislante A:
a) Calor transferido por metro cuadrado:
Q ∆T 500 − 40 920
2
=
=
=
Kcal / m .h
n.0,02
A nR
n
0,04
, de donde
b) Costo del calor perdido:
920 Kcal 24 h 340 d S / .32
240
.
.
.
=
2
6
n. m .h 1d 1año 10 Kcal
n
c) Costo del material:
26 n S / .
15 m 2 .año
d) CostoTotal =
240 26n
+
n
15
e) Variación del costo con el espesor:
dC
240
= − 2 + 1,73
dn
n
S /.
2
m .año
n = número de planchas.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
f) Para costo mínimo:
26.
dC
=0
dn
Por lo que, n = 12
Haciendo lo mismo para el aislante B, resulta:
CostoTotal =
180 40n
+
n
15
dC
180
= − 2 + 2,67
dn
n
Por lo que, n = 8
Reemplazando los valores de n en cada costo total, res ta que el aislante A es el
conveniente para la compra y con ello se logra la rentabilidad y el cuidado al
medioambiente.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
27.
CAPITULO III
TRANS FERENCIA DE CALOR POR CONVECCIÓN
3.1. Impo rtancia
La importancia de la convección para la problemática ambiental, radica en
conocer que este tipo de transferencia de calor se da especialmente en el aire y
en consecuencia, si el mismo se sobrecalienta origina
s problemas como
cambio climático, etc. Por tal razón es importante conocer este estudio a fin de
evitar el sobrecalentamiento de la Tierra. Asimismo, es importante porque ilustra
todas las formas de convección a producirse y de qué manera podemos actuar
para su control.
3.2. Es tudio
En este capítulo se estudiará la clasificación de la t ansferencia de calor por
convección y sus múltiples clasificaciones, a fin que
alumno conozca su
aplicación a nivel natural y por actividades antrópica . Haciendo la salvedad que
este tipo de transferencia de calor se da en fluidos en movimiento, siendo los más
abundantes agua y aire.
3.3. De finició n de Trans fe re ncia de c alor por c onve c c ió n
Kern (2003), la define como el calor producido por dif rencia de temperatura entre
fluidos o en contacto con un cuerpo fijo.
El modelo matemático de la Transferencia de calor por Convección fue dado por
Ley de Newton y Mc Cabe (1995), muestra su ecuación (3.1.)
Q = h . A . ?T
(3.1.)
De la ecuación (3.1.), las variables: Q es el calor transferido por convección, h es
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
el coeficiente de convección, A es la superficie de ca
28.
ción y ? T es el gradiente
de temperatura. El valor de h es determinado de acuerdo al tipo de convección,
para lo cual se utilizan modelos matemáticos que la ciencia los ha aceptado y que
daremos a conocer más adelante.
3.4. Tipo s de trans fere nc ia de c alor por c o nve c c ió n
Los tipos son:
• Convección forzada.
• Convección Natural.
• Convección por Condensación
3.5. Conve c c ió n forz ada
Definición: Se entiende por convección forzada, a la transferencia
calor dado
entre fluidos que se trasladan por influencia antrópica. Esta convección se
clasifica en convección forzada al interior y exterior de tubos y, su estudio se
realiza por separado y comprende lo siguiente:
a) Convección al inte rio r de tubo s
Basa su estudio según el tipo de movimiento de los fluidos másicos. Es decir, si
es laminar o turbulento, el mismo que se debe determinar previo cálculo del
Número de Reynold (Re), para laminar:
Re <2100
turbulento Re> 2100.
a.1) Para flujo turbulento :
Que es lo mismo decir Re > 2100. Para este caso se utiliza la Ecuación de
Dittus – Boelter:
Nu = 0,023 Re0,8. Pr 0,33
De la ecuación (3.2.), las variables: Nu es el número
número de Reynold, Pr es el número de Prandlt.
(3.2.)
Nusset, Re es el
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
29.
Casos especiales:
• Para gases:
Nu = 0,021 Re 0,8
(3.3.)
• Para flujo isotérmico:
h = 0,023(G0,8 / D0,2) (c0,4. k0,6/µ0,4 )
(3.4.)
• Para fluidos muy viscosos con Re < 8000, se usa la Ecuación de Sieder y
Tate:
Nu = 0,027 Re 0,8 . Pr 0,333 (µ / µw) 0,14
(3.5.)
• Para líquidos de conductividad grande (metales fundidos)
h = 7 + 0,025 Pe 0,8
(3.6.)
Asimismo, los números Nusset (Nu), Prandth (Pr), Peclet (Pe) y Reynold (Re),
sus modelos se expresan en las ecuaciones (3.7.), (3.8 ), (3.9.) y (3.10.).
Nu = h.D / k
(3.7.)
Pr = c.u / k
(3.8.)
Pe = D.G.c / k
(3.9.)
Re = D.? .? / µ
(3.10.)
De estas ecuaciones (G) es la velocidad másica y como estos modelos
corresponden a un número, es la razón que sus valores son adimensionales.
a.2.) Para flujo laminar:
Definido flujo laminar para Re < 2100. Para este flu
Nu = 2 (w.c/k.L)
1/3
utiliza:
(µ / µw) 0,14
Casos especiales:
• Cuando la temperatura externa sea igual que la pared:
(3.11.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
Nu = 2 w.c/ p .k.L
30.
(3.12.)
• Para fluidos poco viscosos o cuando ? T es grande:
= 1,75 (µ / µw) 0,14 . [ (w.c/k.L) (1 + 0,015 Z)1/3 ]1/3
Nu
Aquí:
y
(3.13.)
Z = L2.Gr.Pr / D2
(3.14.)
Gr = (g. D3 /v2) (ß.? T)
(3.15.)
b) Convecc ión en el exterio r de tubo s
También basa su estudio según el tipo de movimiento de los fluidos másicos, esto
es a flujo turbulento y laminar.
b .1) Para flujo turbulento :
•
Para líquidos: Nu = Pr 0,3 (0,35 + 0,47 Re 0,52)
(3.16.)
•
Para gases : Nu = 0,26 Pr 0,3 . Re 0,6
(3.17.)
•
Para gases diatómicos o aire:
Nu = 0,32 + 0,43 Re 0,52
•
(3.18.)
Para líquidos a través de espacio anular de tubos concéntricos, se aplica
la Ecuación de Davis:
(h/c.G) = 0,029 (D.G/ µ) -0,2 (c. µ/ k) -2/3 (µ / µw) 0,14 (De/Di) 0,15
(3.19.)
b .2) Para flujo laminar:
Según el tipo de fluido y/o rango de su Reynolds, estos pueden ser estudiados
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
31.
con los siguientes modelos:
• Para líquidos con 0,1 < Re < 200:
Nu = 0,86 Pr 0,3 . Re 0,43
(3.20.)
• Para líquidos: Re > 200 y gases 0,1 < Re < 1000:
Nu = Pr 0,3 (0,35 + 0,47 Re 0,52 )
(3.21.)
• Para gases diatómicos o aire:
Nu = 0,24 Re0,6
(3.22.)
3.6. Conve c c ió n Natural
Definición: Chopey y Tyler (1995), sustentan que es un tipo de calor originada
por corrientes naturales como el aire y demuestran que este tipo de convección es
producto del intercambio de calor por acción de las ma as a condiciones propias
de la naturaleza, que para el caso de superficies verticales y hor
ntales se
aplican las condiciones de la Tabla Nº 01.
De la Tabla Nº 01., las variables b , v y ∆T sus modelos están en función de:
1  v2 − v1 
b = 

v  t 2 − t1  ,
v=
v2 + v1
2
y
∆T = Diferencia de temperatura entre la superficie y el tubo.
Caso especial, cuando el fluido es aire o el flujo es
nar, se aplica los
siguientes modelos, donde D y L están en metros:
• Para paredes horizontales hacia arriba:
h = 2,1 (∆T )
0, 25
(3.27.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
32.
• Para paredes horizontales hacia abajo:
h = 1,1 (∆T )
(3.28.)
• Para paredes verticales ( L > 0,4 m)
:
h = 1,5 (∆ T )
(3.29.)
• Para paredes horizontales hacia abajo:
h = 1,1 (∆T )
(3.30.)
• Para paredes verticales (L < 0,4 m)
 ∆T 
h = 1, 2.

 L 
0, 25
0, 25
:
• Para tubos horizontales y verticales
:
0, 25
 ∆T 
h = 1,1.

 D 
0, 25
(3.31.)
0 , 25
(3.32.)
TABLA Nº 01 : MODELOS PARA EL COEFICIENTE CONVECTIVO
S UPERFICIES
VERTICALES
CONDICIÓN
S UPERFICIES
HORIZONTALES
Re > 10000
2
 0,5.h  c.u.  3



 c.G  k 
0,13
=
 L.G 


 u 
0,13
1
3
1
=
 D.G  3


 u 
(3.23.)
100 = Re = 10000
1
 0,5.h  c.u  4



 c.G  k 
0,59
=
 L.G 


 u 
0,53
1
2
1
=
 D.G  2


 u 
(3.24.)
Re = 100
5
 0,5.h  c.u  6



 c.G  k 
Donde:
G
1,36
=
=
Fuente: GIANKOPLES (1998).
 L.G 


 u 
1,09
2
3
2
(g.b .∆T .r .L)
2
1
2
=
 D.G  3


 u 
=
(g.b .∆T .r
(3.25.)
.D)2
1
2
(3.26.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
33.
3.7. Conve c c ió n por Co nde ns ac ión
Definición: Es una convección originada producto de la condensación del vapor y
se clasifica su estudio para superficies verticales y para tubos horizontales, de tal
manera que el cálculo del coeficiente de condensación h” es posible por la
existencia de modelos definidos para casos diferentes, cuyo estudio es el
siguiente:
a) Condens ació n para s uperficies ve rticales
Para este caso se aplica el siguiente modelo:
1
 k 3 .r 2 .g .l  4

h = 1,13.
 L.u (tv − tw)


(3.33.)
De esta expresión, las variables que se indican sus unidades son:
? = Calor latente de condensación en Kcal/Kg.
g = Gravedad con valor 1,27x 108 m/h 2.
L = longitud de la superficie en m.
tv y tw = Temperaturas del vapor y de la pared en ºC.
u (Viscosidad dinámica), ? (densidad), k (conductividad térmica), todos en
unidades métricas M.K.S.
b) Condens ación para tubo s ho rizo ntales
Este tipo de transferencia de calor a su vez se clasifica por el interior y exterior de
tubos.
b.1. Po r el interio r de tubo s
De igual forma se clasifica para fluidos anulares y en forma estratificado.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
34.
b.1.1. Fluido s Anulares
Un fluido es anular cuando pasa por el espacio de dos ubos concéntricos y
dependiendo de la calidad de los fluidos tanto de ReL como de ReV , se aplican los
siguientes modelos:
I.- Para ReL > 5000
ó ReV > 20 000
1
h.D
 c.u  3  D.Ge 
= 0,0265 
 .

k
 k   u 
0 ,8
(3.34.)
1
 r l 2
Ge = Gl + Gv. 
rv
De esta expresión:
(3.35.)
Precisando que Ge, Gl y Gv son las velocidades másicas equivalentes del líquido
y del vapor, de igual forma ReL y ReV son los números de Reynolds del líquido y
del vapor respectivamente.
II.- Para ReL < 5000
ó ReV < 20 000
1
1
3
h.D
 c.u   D.Ge 
= 5,03.  .

k
 k   u 
3
(3. 6.)
También se aclara que:
Re =
L
D.Gl
u
y
 D.Gv   r l 
ReV = 
. 
 u  rv
1
2
b.1.2. Flujo Es tratificado
Un flujo es estratificado cuando se da a través de var os tubos con arreglos
simétricos. Para este caso se utiliza el siguiente mod lo:
1
 r l 2 . g .L  3

h = 0,767 .k .
n
.
u
.
W


(3. 7.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
De esta expresión, “L” corresponde a la longitud del t
35.
y “n” al número de tubos.
b.2. Po r el exterio r de tubo s
En este caso va depender del tipo de fluido tanto lami
r o turbulento, así se
tiene.
b.2.1. Fluido laminar
Se aplica el siguiente modelo:
1
1
 r l 2 .g .n. p  3  1  6
 .
h = a.k .

u
.
W

  Nr 
(3.38.)
Aquí “Nr”, es el número de hileras verticales y está dado por el siguiente modelo:
Nr =
m.Ds
s
(3.39.)
De estas expresiones, la variable “a y m” son constantes cuyos valores depende
del tipo de arreglo de los tubos, los mismos que son:
•
Arreglo cuadrado, a = 0,856
•
Arreglo triángulo, a = 0,951
•
Arreglo cuadrado, m = 1,0
•
Arreglo triángulo, m = 1,155
Y “s” corresponde al claro de los tubos entre sus cent os.
b.2.2. Fluido turbulento
También denominado mecanismo de rompimiento del vapor
siguiente modelo:
1
1
h.D
 D.r l.VG  2  1  6
= b.
 .

k
 u   Nr 
(3.40.)
se aplica el
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
36.
De esta expresión, la variable “b” tiene los siguientes valores:
• Cuando los tubos están formados en cuadrado, a = 0,39
• Cuando los tubos están formados en triángulo, a = 0,42
En cuanto a “VG”, es la velocidad del gas y está dado por el siguiente
VG =
Wv
r v.af
delo:
(3.41.)
Aquí “ af ” corresponde al área de flujo y cuyo modelo es:
af =
B.Ds.( s − D)
s
(3.42.)
La relación del flujo másico del vapor y el flujo másico del condensado está dado
por el siguiente modelo:
W W
Wv = W − (n'−1) −
n' 2n'
(3.43.)
En estas expresiones las variables B, D, Ds, W, Wv, ?v y n’, corresponden al claro
entre placas deflectoras, diámetro exterior de un tubo diámetro de la cubierta del
haz de tubos, flujo másico del condensado, flujo másico del vapor, densidad del
vapor y número de placas deflectoras respectivamente.
PROBLEMAS APLICATIVOS
PROBLEMA 3.1.
El parabrisas de un automóvil se desempaña mediante el paso de aire caliente a
Ti = 40 ºC sobre su superficie interna. El coeficiente d
convección en esta
superficie es hi = 30 [W/m2 - ºK]. La temperatura del aire ambiental es Tinf = -10 ºC
y el coeficiente de convección es hc = 65 [W/m2 - ºK].
1. Calcular las temperaturas de las superficies interna y externa del
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
37.
parabrisas de vidrio que tiene 4 [mm] de espesor. (kvidrio(a 300 ºK) = 1,4
[W/m - ºK]).
2. Dibuje perfiles (en forma cualitativa) de temperatura
el parabrisas
tuviese: Doble vidrio con aire, doble vidrio con agua si tuviera curvatura.
S OLUCIÓN:
(1) En un esquema general tenemos lo siguiente:
Ti = 40ºC
Tw i
Dentro del
automóvil
Fuera del
automóvil
Tw o
T inf = -10ºC
Figura Nº 3P-1: Figura del problema 3.1.
Para la transferencia de calor a nivel global se tiene que:
q Ti − Tinf
=
A
RT
Donde la Resistencia Total se calcula como sigue:
RT =
1 1 ∆x
+ +
hi hc k w
Entonces:
RT =
[
2
1 1 ∆x
1
1
4 × 10−3 [m]
+ +
=
+
+
= 0,052 m −º K W
W
W
W
hi hc k w 30
65
1,4 m− º K
m2 −º K
m2 −º K
[
] [
] [
[ ]
q Ti − Tinf
(40 − ( −10))º K
=
=
= 961,54 W 2
2
m
A
RT
m
−
º
K
0,052
W
[
]
Luego, se tiene en las interfases de aire en convección:
-
In te rna
]
]
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
38.
q
q
= hi × (Ti − Twi ) ⇒ Twi = Ti −
A
hi × A
Twi = Ti −
[ ]
[ ]
961,54 W 2
q
m
= 40º C −
W
hi × A
30
m2 −º C
Twi = 7,95º C
-
Exte rna
q
q
= hc × (Two − Tinf ) ⇒ Two = Tinf −
A
hc × A
Two = Tinf +
[ ]
[ ]
961,54 W 2
q
m
= −10º C +
W
hc × A
65
m2 −º C
Two = 4,79 º C
-
Cas o (a): Vidrio con aire
Ti = 40ºC
Twi
Fuera del
automóvil
Dentro del
automóvil
Tw o
Tinf = -10ºC
Pendiente grande:
AIRE CONDUCE
POCO
Figura Nº 3P-2: Figura del problema 3.1.
-
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
-
39.
Cas o (b): Vidrio con agu a
T i = 40ºC
Tw i
Dentro del
automóvil
Fuera del
automóvil
Two
T inf = -10ºC
Pendiente pequeña:
AGUA CONDUCE MÀS
QUE A IRE
Figura Nº 3P-3: Figura del problema 3.1.
-
Cas o (c): Vidrio con curvatura
Perfil
logarítmico por
la ecuación de
transferencia
Ti = 40ºC
Dentro del
automóvil
Fuera del
automóvil
Twi
Two
Tinf = -10ºC
Figura Nº 3P-4: Figura del problema 3.1.
PROBLEMA 3.2
Un alambre eléctrico de 3 mm. de diámetro y 5 m. de largo está firmemente
envuelto con una cubierta gruesa de plástico de 2 mm. de espesor, cuya
conductividad térmica es k = 0,15 [W/m – ºC]. Las mediciones eléctricas indican
que por el alambre pasa una corriente de 10 A y se tie
na caída de voltaje de
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
40.
8 V a lo largo de éste. Si el alambre aislado se expone a un medio que está a Tinf
= 30 ºC, con un coeficiente de transferencia de calor de h = 12 [W/m2-ºK],
determine la temperatura en la interfase del alambre y la cubierta de plástico en
operación estacionaria.
S OLUCIÓN:
Podemos esquematizar el problema como sigue:
k
r1
r2
T2
H,T inf
T1
Q
Figura Nº 3P - 5: Figura del problema 3.2.
Un alambre eléctrico está firmemente envuelto con una
bierta de plástico. Se va
a determinar la temperatura de la interfase.
Supondremos que:
1. La transferencia de calor es estacionaria ya que no hay indicación del
algún cambio con el tiempo.
2. La transferencia de calor es unidimensional dado que s
tiene simetría
térmica con respecto a la línea central y no hay variación en la dirección
axial.
3. Las conductividades térmicas son constantes.
4. La resistencia térmica por contacto en la interfase es despreciable.
5. En el coeficiente de transferencia de calor se incorporan los efectos de la
radiación, si los hay.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
41.
Además se conoce la siguiente propiedad:
La conductividad térmica del plástico es k = 0,15 [W/m-ºC]. Entonces:
-
En el alambre se genera calor y su temperatura se elev como resultado
del calentamiento por resistencia. Se supone que el ca
se genera de manera
uniforme en todo el alambre y se transfiere hacia el medio circundante en la
dirección radial. En la operación estacionaria, la velocidad de la transferencia de
calor se vuelve igual que el calor generado dentro del alambre, el cual se
determina que es:
•
Q = W e = V ⋅ I = 8V ⋅ 10 A = 80W
-
La red de resistencias térmicas para este problema comprende una
resistencia a la conducción, para la cubierta de plást
convección, para la superficie exterior, en serie. Se
y una resistencia a la
rmina que los valores de
estas dos resistencias son:
A2 = (2pr2 ) L = 2p (0,0035m) ⋅ (5m) = 0,110m2
Rconv =
R plástico =
[ m ]⋅ 0,110[m ]
1
=
hA2 12 W
1
2
[ W]
= 0,76 º C
2
[ ]
ln( r2 r1 )
ln(3,5 1,5)
=
= 0,18 º C
W
W
2pkL
2p (0,15
) ⋅ 5[m ]
m
[ ]
Y, por lo tanto:
[ W]
Rtotal = R plástico + Rconv = 0,76 + 0,18 = 0,94 º C
-
Entonces, se puede determinar la temperatura en la interfase a partir de:
Q=
T1 − Tinf
→ T1 = Tinf + Q ⋅ Rtotal
Rtotal
T1 = Tinf + Q ⋅ Rtotal
[ W]
T1 = 30º C + (80W ) ⋅ 0,94 º C
T1 = 105 º C
Con lo cual queda demostrado que la temperatura en la interfase es de 105 ºC.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
42.
CAPÍTULO IV
TRANS FERENCIA DE CALOR POR RADIACIÓN
4.1. Impo rtancia
La importancia de la radiación es que permite conocer que el calor por radiación
es el único que no necesita un medio para transferirse y puede causar grandes
problemas ambientales como son los rayos del Sol. Asimismo, este estudio es
importante a la problemática ambiental porque resuelve estos problemas al evitar
perdidas de calor en sistemas que trabajan a altas tem
raturas como son hornos
y calderos y, de esta manera permite optimizar el consumo de recursos para la
producción de energía. También, es importante porque ilustra todas las formas de
radiación a producirse y de qué manera podemos actuar
ra su control.
4.2. Es tudio
En este capítulo se estudiará el calor transferido por radiación a nivel de cuerpos
planos y cilíndricos, con o sin aislante, de manera de minimizar las pérdidas de
calor y por consiguiente optimizar el recurso. Para el o se desarrollará los
siguientes ítems:
•
Definición del calor por radiación.
•
Radiación en cuerpos planos.
•
Radiación en cuerpos cilíndricos
4.3. De finició n del c alor por radiac ió n
La radiación es el calor transferido entre cuerpos separados que no tienen vínculo
de unión, tal es el ejemplo del calor transferido del Sol a la Tierra; donde el Sol es
la fuente y la Tierra es el recibidor, así esquemáticamente se muestra en la Figura
4.1.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
43.
En la radiación, todo cuerpo cumple el siguiente funda ento:
a + r + t
=
1
(4.1.)
De la ecuación (4.1.), las variables a , r y t corresponden a la absorbancia,
reflexividad y transmitividad.
Qa
Qr
Qt
FUENTE
RECIBIDOR
Qe
Qa
Leyenda:
Qe = Calor emitido.
Qa = Calor absorbido.
Qr = Calor reflejado.
Qt = Calor transferido.
Figura Nº 4.1.: Trans mis ión de l c a lor por radiac ión.
Los tipos de cuerpos que existen son: negro, gris y transparente. La aplicación de
la ecuación (4.1.) en estos cuerpos resulta:
•
En cuerpo negro
:
•
En cuerpo gris
:
•
En cuerpo transparente :
a = 1
a + r = 1
t = 1
Es importante conocer los tipos de cuerpos, pues en fu ción de ellos se podrá
tomar decisiones que cuerpos utilizar en los diseños de equipos, lo que conlleva a
conocer la emisividad (e), estudiado por Kirchhoff.
a) Ley de Kirchhoff
Relaciona la emisividad (e) con la absorbancia ( a ), donde la energía de cualquier
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
44.
cuerpo (Ec) y la energía de un cuerpo negro (En), resu a:
Ec
= a =e
En
(4.2.)
b) Calor po r Radiació n
Tomando en cuenta a Kirchhoff, Stefan-Boltzmann determinó que el calor
transferido por radiación es:
Q = s .e . A.T 4
(4.3.)
De esta expresión, s , e, A y T son las variables constante de Stefan-Boltzmann de
valor
0,173x10-8
BTU/(h.ft2 .ºR4), emisividad, superficie de calefacción y
temperatura alcanzada.
4.4. Aplic ac io ne s del c alor por radiació n
Su aplicación es:
• Calor de radiación entre cuerpos.
• Calor de radiación perdido en cuerpos planos y cilíndricos.
4.5. Calor de radiac ió n e ntre c ue rpo s
Dependiendo del tipo de plano, el calor de radiación entre cuerpos puede ser:
a) Entre plano s finito s
Formulando balance térmico, se tiene:
Qneto = Q emitido
-
Qabsorbido
Q = s .e1. A1.T 14 − s .e 2. A2.T 24
(4.4.)
(4.5.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
45.
b) Entre plano s infinito s
Para este caso Kern (2001), demuestra que se cumple:
(
Q
s
4
4
=
T1 − T 2
A  1  1 
  +   −1
 e1   e 2 
)
(4.6.)
4.6. Calor de radiac ió n pe rdido e n c uerpo s plano s y cilíndric o s
La naturaleza por estar rodeado de aire, el calor perdido está expresado por:
Q = Qr
+ Qc
(4.7.)
De donde; Q (calor perdido), Qr (calor de radiación) y Qc (calor convectivo). En
base a este modelo se aplican en los siguientes casos:
a) Pérdida de calo r en s uperficie des nuda
Se define superficie desnuda a la superficie que no tiene aislamiento y por tanto
no está protegido para maximizar el aprovechamiento del calor. Para este caso se
aplica el siguiente modelo:
5 V + 68,9
 T1 + 460 4  Ta + 460  4 
Q
= 0,173.e 
 −
  + 0,296(T 1 − Ta )4
A
68,9
 100   100  
(4.8.)
b) Pérdida de calo r en s uperficies ais ladas
Una superficie aislada es naturalmente más ventajoso en el uso del calor y para
su evaluación se aplica el siguiente modelo:
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
5 V + 68,9
 Ts + 460  4  Ta + 460  4 
Q
= 0,173.e 
 −
  + 0,296(Ts − Ta )4
A
68,9
 100   100  
46.
(4.9.)
c) Cálculo de la temperatura s upe rficial co n ais lamiento
Para este caso se procede a determinar según la forma del sistema, es decir si es
plana o cilíndrica, cuyos modelos se muestran:
c.1. S uperficies planas
Aplicando los criterios de superficie plana, se tiene:
5 V + 68 ,9
 Ts + 460  4  Ta + 460  4 
T 1 − Ts
= 0,173 .e 
 −
  + 0,296 (Ts − Ta )4
L
68,9
 100   100  
k
(4.10.)
c.2. S uperficies cilíndricas
Aplicando los criterios de superficie cilíndrica, se tiene:
5 V + 68,9
 Ts + 460  4  Ta + 460  4 
T1 − Ts
= 0,173.e 
 −
  + 0,296(Ts − Ta )4
r2
68,9
 100   100  
r 2 ln
r1
k
(4.11.)
En todos estos modelos, “V” es la velocidad del viento en ft/min, T1 es la
temperatura de la superficie desnuda, Ts es la temperatura del aislamiento y Ta
es la temperatura del ambiente, en donde las temperaturas están en ºF. La
variable “L” es el espesor del aislamiento en superficie plano y, r2 y r1 son los
radios que limitan el espesor en superficies cilíndricas.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
47.
PROBLEMA APLICATIVO
PROBLEMA 4.1.
La temperatura de una superficie plana de hierro es 400 ºF, aislado con 3” de
Insul Quick (k = 0,3 BTU/h.ft.ºF), está expuesto a una temperatura ambiental de
20 ºC, con velocidad de viento 0 ft/min; las emisivida
del material hierro y del
aislante son 0,3 y 0,2 respectivamente. Hallar la temperatura superficial del
aislante.
S OLUCIÓN:
Aplicando la ecuación (4.10.), expresada como:
5 V + 68,9
 Ts + 460  4  Ta + 460  4 
T 1 − Ts
= 0,173.e 
 −
  + 0,296(Ts − Ta )4
L
68,9
 100   100  
k
Y reemplazando en ella los datos del problema:
Ta = 20 ºC, e =0,2, T1 = 400 ºF, L = 3”, k = 0,3 BTU/h.ft.ºF, V = 0 ft/min
y hallando Ts, que es la temperatura superficial del aislante;
resulta:
Ts = 100 ºF
Por lo que, el aislante permite una perdida de calor con el medio ambiente
alcanzando dicho aislante una temperatura de 100 º F, el cual es satisfactorio.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
48.
CAPITULO V
INTERCAMBIADORES DE CALOR
5.1. Impo rtancia
En este capítulo básicamente es la aplicación de los a
riores capítulos y basa
su estudio a nivel de equipos industriales. Su importancia para la problemática
ambiental es que aporta con conocimientos a fin de controlar las operaciones y
eficiencia de sistemas productivos que utilicen intercambiadores de calor, de tal
manera que se aproveche lo máximo la energía y de esta manera evitar consumir
en exceso los recursos contribuyendo al desarrollo sostenible de nuestro planeta.
Además, su aplicación permite tratar térmicamente cual uier solución o
aprovechar la energía de un fluido para evitar innecesariamente utilizar energía no
renovable para el mismo fin. Con ello, este capítulo contribuye al manejo del calor
para darle el máximo aprovechamiento y de esta manera mantener nuestro
ambiente y al mismo tiempo da un valor agregado de rentabilidad a las empresas,
ya que, ahorran en costos por energía.
5.2. Es tudio
El estudio comprende el diseño y evaluación de interca biadores de calor de tipo
horquillas y tubo-coraza. Haciéndose la evaluación calorífica y caída de presión,
aceptándose un límite de ?P = 10 lb/in2, de acuerdo al diseño de equipos de
intercambio de calor dado por Manufacturers Association (1960). El estudio inicia
con el sistema de intercambio de calor a doble tubo, que es un sistema ideal y a
partir de ello hacer el estudio de los equipos reales tilizados en la industria.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
49.
5.3. Inte rc ambiado r de c alo r
Definición: Son equipos industriales que permiten calentar o enfriar fluidos,
aprovechando el calor del otro sin entrar en contacto directo; pues estos fluidos
intercambian calor a través de paredes que los separa.
5.4. Tipo s de inte rc ambiado re s de c alor
Los tipos son:
• Horquillas.
• Tubo-coraza.
5.5. Inte rc ambio de c alor a Do ble Tubo
Kern (2001), el intercambio de calor a doble tubo que consiste de dos tubos, en
donde un tubo se encuentra en la parte central dentro
otro tubo de mayor
diámetro sin tocar sus paredes. Este sistema es ideal
uesto que se da en
tuberías infinitas, lo cual nunca sería factible su instala
n en cualquier empresa.
Su importancia radica que sienta las bases teóricas pa a el estudio de las
horquillas.
Este tipo de intercambiador de calor son de dos tipos:
• A flujo contracorriente.
• A flujo paralelo.
Es de enfatizar que el primero es más eficiente, estos sistemas forman dos zonas
muy bien definidas como son la zona anular y tubular.
La zona anular es la parte formada por el espacio que
a el tubo de menor
diámetro dentro del tubo mayor y, la zona tubular es el espacio formado por el
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
50.
diámetro del tubo de menor diámetro.
En estos modelos se aplica la media logarítmica (MLDT), cuya expresión es la
siguiente:
MDLT =
∆T 2 − ∆T 1
∆T 2
ln
∆T 1
(5.1.)
Las variaciones de temperatura, según el modelo son:
a) Sistema en paralelo:
?T2 = T1 – t1,
?T1 = T2 – t2
b) Sistema en contracorriente:
?T2 = T1 – t2,
?T1 = T2 – t1
L
L
T1
T2
t1
t2
T1
T2
t1
T2
t2
L
t2
t1
? T1
Fig ura Nº 5.1.: Doble tubo e n
parale lo
t2
T1
T2
t1
? T2
T1
? T1
L
? T2
Figura Nº 5.2.: Doble tubo e n c ontrac orrie nte
Para efectos de cálculos llamaremos. MLDT = ?T
Luego, aplicando el principio de transferencia de calo (Q) resulta:
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
Q = U.A.?T
51.
(5.2.)
De esta última ecuación, A es la superpie de calefacción y U el coeficiente global
de transferencia de calor.
Para determinar “U”, se basa su estudio por el intercambio simultáneo de calor
por convección y conducción y su determinación es a partir de la definición de la
resistencia global, la misma que es igual a la suma de las dos resistencias
convectivas y una conductiva que se da en el tubo interior de los tubos
concéntricos, cuyo modelo resultante es el siguiente:
1
Ao
=
+
U
hi. Ai
Do
Di + 1
2k
ho
Do ln
(5.3.)
De la ecuación (5.3.), hi y ho corresponden a los coeficientes de convección
interna y externa de la zona tubular y, Do y Di a los
etros que forman el
espesor del tubo interior. De igual forma Ai y Ao están en función a los diámetros
antes indicados y k es la conductividad térmica del material del tubo interior.
Tanto hi y ho deben ser determinados mediante la Figura Nº 5.8. que se presenta
en el anexo. En donde se debe previamente calcular el diámetro equivalente (De)
para la parte anular, cuya expresión es la siguiente:
De =
Do2 − Di 2
Di
(5.4.)
Antes de realizar los cálculos es preciso que en el balance de energía se cumpla:
Calor perdido
= Calor ganado; y aplicando la prim
resulta:
w1.c1.? T*1 = w2.c2.? T*2
(5.5.)
ley de la termodinámica
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
52.
Las variables de la ecuación (5.5.), corresponden a los flujos másicos (w1 y w2),
calores específicos (c1 y c2) y las variaciones de temperatura de cada flujo (? T*1
y ?T*2).
5.6. Inte rc ambiado r po r Horquillas
Este equipo se diseña en base a doble tubo, cuya aplicación es realista y su
diseño debe estar controlado por dos variables fundamentalmente como son
factor de obstrucción total (Rd) y caídas de presión (?P). Los intercambiadores de
horquillas se construyen con uso de tubos mayores o ig
l a 20 pies de calidad
BWG y su diseño está en función a la cantidad de flujo que soportaran y pueden
ser: En Serie y en Serie-Paralelo.
Rdo
Tubo
mayor
Rdi
ho
hio
hi
Tubo
menor
Figura Nº 5.3.: Indic ado re s de obs truc c ión y c oe fic ie n e s de c onve c c ió n
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
Fig u ra Nº 5.4.: Ho rqu illa e n s e rie
Fig ura Nº 5 .
53.
Ho rq u illa s e rie p a rale lo
Fuente: Kern (2001).
Los modelos matemáticos de diseño comunes para ambos tipos de horquillas
mencionados se desarrollan a partir de la Figura Nº 5.1. en donde se desprecia la
conducción por tener el tubo interior una pared muy delgada, para lo cual se
utiliza las siguientes expresiones:
hio = hi
Ai
Di
= hi
Ao
Do
(5.6.)
Aplicando el Coeficiente Total de Transferencia de calor “Ud”, se tiene:
1
1
=
+ Rd
Ud Uc
(5.7.)
De donde:
1
1
1
= Rio + Ro =
+
Uc
hio ho
(5.8.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
Rd = Rdi + Rdo
54.
(5.9.)
NOTA: Tanto hi y ho se obtienen utilizando la Figura N 1A.
El calor transferido por estos equipos, es evaluado ut zando el siguiente modelo:
Q = Ud.A.?T
(5.10.)
De la ecuación (5.10.), la variable ?T está definida como MLTD.
a) Horquillas a flujo en S erie
En este tipo de horquilla la ecuación (5.10.), el MLTD está definida según la
ecuación (5.1.).
b) Ho rquillas a flujo S erie-Parale lo
En este tipo de horquilla la ecuación (5.10.), el MLTD está definida según la
ecuación:
MLTD = Y (T1 – t1)
(5.11.)
La variable “Y” de la ecuación (5.11.) se aplica en los siguientes casos:
b.1. Para una corriente caliente en serie y n corrient

1 − P′
 R ′   R′ − 1  
= 2,3 n
 log 

Y
 R′ − 1   R′ 


1

P′ 
1
n

1
+ 
R′ 

frías en paralelo.
(5.12.)
De donde:
R′ =
T1 − T 2
n(t 2 − t1)
(5.13.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
P′ =
T 2 − t1
T 1 − t1
55.
(5.14.)
b.2. Para una corriente fría en serie y n corrientes calientes en paralelo.



1 − P′′
n
= 2,3
log (1 − R ′′) 
Y
1 − R′′ 


1 

P ′′ 
1
n


+ R′ 


(5.15.)
De donde:
R ′′ =
n(T 1 − T 2)
t 2 − t1
(5.16.)
P′′ =
T1 − t 2
T 1 − t1
(5.17.)
Cálc ulo de propiedade s
Tomando en cuenta la Figura Nº 5.2. y para fluidos der vados del petróleo, se
utiliza la Figura Nº 2A., de donde:
∆tc ∆T 1 T 2 − t1
=
=
∆th ∆T 2 T 1 − t 2
(5.18.)
Para este caso es necesario determinar las temperaturas calóricas (Tc y tc),
cuyos modelos son:
Tc = T 2 + Fc (T 1 − T 2)
tc = t1 + Fc (t 2 − t1)
(5.19.)
(5.20.)
También es necesario hallar “Tw” o temperatura de la pared, para ello se utiliza el
siguiente modelo:
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
56.
ho
Tw = tc +
hio
Φt
Φa
+ ho
(Tc − tc )
Φa
(5.21.)
Donde:
 m
 mw 


0,14
0 ,14
Φa = 
 m
 mw 


Φt = 
y
(5.22.)
NOTA: Para la realización de estos cálculos, se debe utilizar la Figura Nº 1A., de
h
donde se despeja
Φ.
A partir de estos cálculos previos, se puede determinar “ho y hio”. Es decir,
utilizando la siguiente expresión:
h
.Φ
Φ
h=
(5.23.)
Cálc ulo de caídas de pres ió n en ho rquillas :
I. Lado tubo :
Para el fluido que pasa por el tubo interior, llamado lado tubo la caída de presión
de dicho fluido se determina utilizando los siguientes modelos:
f = 0,0035 +
0,264
 D.G 


m


0, 42
(5.24.)
Con uso de la Ecuación de Fanning, se tiene:
2
∆Ft = 2
f .G .L
2
g . r .D
La caída de presión resulta:
(5.25.)
∆P = ∆Ft .r
(5.26.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
57.
II. Lado ánulo :
Para el fluido que pasa por la zona anular del interca biador de calor, la caída de
presión se determina utilizando las siguientes expresiones:
f = 0,0035 +
0,264
 De.G 


m


0, 42
(5.27.)
Luego, las pérdidas son:
2
∆Fa =
2 f .G .L
2
2 g . r .De
∆Fl = N V
(5.28.)
2
2g
(5. 9.)
La caída de presión resultante es:
∆Pa = ( ∆Fa + ∆Fl ) r
NOTA: Aquí,
(5.30.)
De = D2 − D1
5.7. Inte rc ambiado re s de c alor de Tubo y Coraza
Estos intercambiadores tienen una coraza y por dentro
ios tubos y de ahí
deriva su nombre, estos equipos son para operaciones de grandes volúmenes,
los cuales son de mayor eficiencia que los intercambiadores de horquillas; sus
modelos pueden ser: 1-2, 2-4, 3-6, etc. Dependerá de los pasos en los tubos o en
la coraza. Ejemplo de tipo 1-2, se muestra en la Figura Nº 5.6., cuyos flujos
térmicos son aplicados en el diagrama temperatura vers
longitud del
intercambiador, el que se ilustra en la Figura Nº 5.7. aclarando que las
temperaturas T1 y T2 corresponden al fluido caliente y las temperaturas t1 y t2
corresponden al fluido frío.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
58.
Se denomina paso cada vez que un fluido cambia de dirección opuesta, para lo
cual mínimo necesita dos tubos apara tener dos pasos, endo cada paso un tubo.
T1
t2
T2
t1
Figura Nº 5.6.: Inte rc amb iador Tubo-Coraza tipo 1-2.
Fuente: Kern (2001).
De las Figuras Nº 5.6 y 5.7. las variables T1 y T2 cor esponden al fluido caliente y
t1 y t2 al fluido frío.
T1
T2
t2
ti
t1
L
Figura Nº 5.7.: Diagrama de variac ión té rmic o e n tubo - c oraza.
Los modelos matemáticos de diseño parten de la figura
5.7. y a continuación
se detalla todos los modelos, teniéndose presente que cuando se tenga que
reemplazar el valor del Diámetro Equivalente (De), se
be tener claro el tipo de
arreglo tubular del intercambiador, los mismos que pueden ser de arreglo
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
59.
triangular o cuadrado, en cada caso las variables Pt y do son distancia de
ro a
centro de los tubos y diámetro externo de un tubo.
Para arreglo triangular, se utiliza:
De =
(3,44 Pt
− p do
p .do
P 2t
2
)
(5.31.)
Para arreglo cuadrado, se utiliza:
2
De =
2
4 Pt − p . do
p .do
(5.32.)
De la Figura Nº 5.7, se obtienen las siguientes ecuaciones:
∆T 2 = T 1 − t 2
(5.33.)
∆T 1 = T 2 − t1
(5.34.)
Para determinar MLDT, se aplica la ecuación (5.1.).
El calor transferido (Q) en estos equipos, es determinado por la ecuación (5.10.),
en donde, el calor transferido está en función del coeficiente global de
transferencia de calor (Ud), la superficie de calefacción (A) y variación de la
temperatura (?T). Estas variables son definidas de acuerdo a las ecuaciones
(5.6.) al (5.9.). Aquí la superficie de calefacción (A), está expresado de la forma
siguiente:
A = N .L.p .do
(5.35.)
De igual manera, “N” representa la cantidad de tubos q
contiene el
intercambiador, “L” longitud del equipo y “do” el diámetro de un tubo. A su vez,
∆T es determinado por la ecuación (5.36.).
∆T = Ft.MLDT
(5.36.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
60.
Ft es un factor que depende del tipo del intercambiador y que es leído en figuras
según el modelo de trabajo; por ejemplo se presenta la Figura Nº 3ª. para
intercambiador tipo 1-2. En estas figuras es necesario conocer el valor de l
variables “R” y “S”, las cuales son determinadas a partir de las temperaturas de
operación, así se tiene:
R=
T1 − T 2
t 2 − t1
(5.37.)
S=
t 2 − t1
T 1 − t1
(5.38.)
Asimismo, para determinar las áreas transversales y caídas de presión se utilizan
los siguientes modelos:
A) ÁREAS TRANS VERS ALES
a) Lado Co raza:
As =
Ds.C ′.B′
Pt
(5.39.)
Donde Ds (diámetro interno de la coraza), C' (Claro en tubos), B' (espacio entre
deflectores).
b) Lado Tubo
At =
N
.ai
n
(5.40.)
Donde N (número de tubos), n (número de pasos) y ai (á a interna de un tubo).
Esto es importante porque para cada caso se puede hallar la
cuyos modelos son:
Para la Coraza:
Gs = Ws / As
y
para el Tubo:
Gt = Wt / At
dad másica,
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
61.
B) CAIDAS DE PRES IÓN
a) Lado Co raza:
Está determinado por:
2
∆P =
f .Gs .Ds ( Nd + 1)
(5.41.)
2.g .r .De.f s
Donde Nd (número de deflectores), L (longitud de un tu
 m
 mw 


), F s es igual a:
0,14
fs =
Está última expresión indica que es un modelo que divide las viscosidades del
fluido parte central del medio con respecto al fluido de la pared.
b) Lado Tubo
Las expresiones son:
2
∆Pt =
∆ Pr =
f .Gt .L.n
10
en lb/in2
(5.42.)
5, 22.10 .Di.s.f t
2.n.V
2
g . s.
(5.43.)
Aquí f (factor de fricción), n (número de pasos), Gt (velocidad másica), s (gravedad
específica), Di (diámetro interno del tubo). V (velocidad del fluido).
La caída de presión total es:
∆P = ∆Pt + ∆ Pr
(5.44.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
62.
C) EFICIENCIA (e)
Tomando en cuenta las temperaturas del intercambiador, resulta:
a) Cuando el fluido frío tiene menor capacidad calórica que el caliente:
e=
t 2 − t1
T 1 − t1
(5.45.)
b) Cuando el fluido frío tiene mayor capacidad calórica que el caliente:
e=
T1 − T 2
T 1 − t1
(5.46.)
PROBLEMAS APLICATIVOS
PROBLEMA 5.1. (Aplic ació n de ho rquillas )
Para la producción de un cierto producto, se requiere ingresar a un reactor un flujo
de agua de 1 800 m3/h a 20 ºC. Sin embargo el agua se extrae desde la red
pública a sólo 8 ºC de tal manera que se aproveche la temperatura del ambiente.
Se pretende instalar un intercambiador de calor de tubos concéntricos el cual
utilizará un fluido de alta temperatura con un flujo de 1000 m3/h a 130 ºC. Se le
solicita dimensionar el área A0 del intercambiador de tubos concéntricos utilizando
un coeficiente de transferencia de calor global U0 de valor 267,8 W/m2 - ºC y si los
datos complementarios son los siguientes:
Cp,agua = 1 [cal/gr - ºC]
Cp,fluido = 0,5 [cal/gr - ºC]
ρagua = 1.000 [kg/m3 ]
ρfluído = 2.500[kg/m3 ]
S OLUCIÓN:
Si se identifican las variables conocidas se tiene: th,in, tc,in, tc,out, flujo frío y flujo
caliente. Este tipo de problemas de dimensionamiento d
intercambiadores de
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
63.
tubos concéntricos posee un algoritmo de solución clásico, para lo cual se
procederá hacer los siguientes cálculos:
1. Cálculo del calor transferido total.
2. Luego, bajo la hipótesis de inexistencia de perdidas de calor, se calculará th,out.
3. Finalmente, el cálculo del área del intercambiador a partir de las ecuaciones de
este capítulo y se utilizarán las siguientes:
QT = U 0 ⋅ A0 ⋅ ∆TL
∆T − ∆T2
∆TL = 1
∆T
ln 1
∆T2
El calor absorbido por el agua se calcula a partir de
siguiente ecuación:
( )
QC = mc p c ⋅ (Tc , out − Tc ,in )
Entonces:
[ ]
3
  ⋅ (20º C − 6º C )
QC =  1800 m
⋅ 1000 kg 3  ⋅ 1 kcal
hr
kg
−
º
C



 
m

 

[
QC = 2,52 × 107 kcal
hr
]
Bajo el supuesto de que no hay pérdidas de calor importantes podemos imponer
que:
QC = QH = QT
Pero además se tiene que:
QH = (mc p )h ⋅ (Th ,out − Th ,in )
Luego:
[
− 2,52 × 107 kcal
]= 1000[m hr ]⋅ 2500kg m  ⋅ 0,5kcal kg −º C   ⋅ (T
3
hr
3
h, out
h
Con lo cual se obtiene:
Th ,out = 109,84º C
− 130º C )
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
64.
S uponer el fluido en Co – corriente o Flujo Paralelo .
Figura Nº 5P-1: Figura del problema 5.1.
Entonces:
∆T1 = Th,in − Tc ,in
∆T2 = Th ,out − Tc ,out
Calculamos:
∆TL =
∆T1 − ∆T2 (130º C − 8º C )− (109,84º C − 20º C )
=
= 105,10º C
∆T
 130º C − 8º C 
ln 1
ln 

∆T2
 109,84º C − 20º C 
Luego se puede obtener el área del intercambiador como:
A0 =
A0 =
QT
U 0 ⋅ ∆TL
1[J ]
1[hr ]
[ ] 0,2389
×
[cal ] 3600[s]
2,52 × 1010 cal hr ×
[ m −ºC ]⋅105,10º C
267,8 W
2
Por lo tanto el área por esta técnica para hacer facti le este aprovechamiento
ambiental es:
[ ]
A0 = 1041,04 m2
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
65.
S uponer el fluido en Contra-co rriente.
Figura Nº 5P-2: Figura del problema 5.1.
Entonces:
∆T1 = Th ,out − Tc ,in
∆T2 = Th,in − Tc ,out
Calculamos:
∆TL =
∆T1 − ∆T2 (109,84º C − 8º C )− (130º C − 20º C )
=
= 105,87º C
∆T
109,84º C − 8º C 
ln 1
ln 

∆T2
 130º C − 20º C 
Luego se puede obtener el área del intercambiador como:
A0 =
A0 =
QT
U 0 ⋅ ∆TL
1[J ]
1[hr ]
[ ] 0,2389
×
[cal ] 3600[s]
2,52 × 1010 cal hr ×
[ m −ºC ]⋅105,87º C
267,8 W
2
Finalmente el área por esta técnica para hacer factible este apr
ambiental es:
[ ]
A0 = 1033 ,47 m 2
ento
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
66.
PROBLEMA 5.2. (Aplic ació n de Tubo-Co raza)
Con la finalidad de evitar calentar glicerina con vapo de agua producida en un
caldero y por consiguiente la quema de combustible en perjuicio ambiental, una
empresa ha decidido usar un intercambiador de dos pasos por el casco y cuatro
pasos por los tubos para calentar la glicerina desde 20 ºC hasta 50 ºC por medio
de agua caliente producida en sus instalaciones que van a terminar en la red del
alcantarillado; esta agua ingresa en los tubos de pared delgada de 2 cm de
diámetro a 80 ºC y sale a 40 ºC. La longitud total de los tubos en el intercambiador
es de 60 m. El coeficiente de transferencia de calor por convección es de 25 W/m2
.ºC del lado de la glicerina (casco) y de 160 W/m2.ºC del lado del agua (tubo).
Determine la velocidad de la transferencia de calor en el intercambiador:
a) Antes de que se tenga incrustación.
b) Después de que se presenta ésta sobre las superficies exteriores de los tubos,
con un factor de incrustación de 0,0006 m2 . ºC/W.
S OLUCIÓN:
Fraficando el intercambiador de calor del problema y rotulando el mismo, se tiene
el siguiente:
Glicerina fría
20 ºC
40 ºC
Agua
caliente
80 ºC
50 ºC
Figura Nº 5P-2: Figura del problema 5.2.
Primero se debe determinar la velocidad de la transferencia de
incrustaciones para lo cual suponemos que:
lor sin y con
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
67.
1. Existen condiciones estables de operación.
2. El intercambiador de calor está bien aislado de modo q
la pérdida de calor
hacia los alrededores es despreciable y, por consiguiente, la transferencia de
calor desde el fluido caliente es igual a la transfere
calor hacia el fluido
frío.
3. Los cambios en las energías cinéticas y potenciales de las corrientes de los
fluidos son despreciables.
4. Los coeficientes de transferencia de calor y los factores de incrustación son
constantes y uniformes.
5. La resistencia térmica del tubo interno es despreciabl
puesto que dicho tubo
es de pared delgada e intensamente conductor.
Se dice que los tubos son de pared delgada y, como consecuencia, resulta
razonable suponer que sus áreas superficiales interior y exterior son iguales.
Entonces, el área superficial de transferencia de calo queda:
As = p ⋅ D ⋅ L = p ⋅ (0,02 m )⋅ (60 m ) = 3,77 m 2
Se puede determinar la velocidad de la transferencia de calor en
ste
intercambiador a partir de:
Q = U ⋅ As ⋅ F ⋅ ∆Tml ,CF
Donde F es el factor de corrección y
∆Tml ,CF
es la diferencia de temperatura media
logarítmica para la disposición a contraflujo, de acuerdo a las ecuaciones
desarrolladas en este capítulo. Estas dos cantidades se determinan a partir de:
∆T1 = Th, out − Tc , in = 40 º C − 20º C = 20 º C
∆T2 = Th ,in − Tc , out = 80 º C − 50 º C = 30 º C
∆Tml ,CF =
∆T1 − ∆T2 20º C − 30º C
=
= 24,7 º C
∆T1
20
º
C


ln
ln 

∆T2
 30º C 
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
P=
y,
R=
Tc ,in − Tc ,out
Th.out − Th ,in
Th ,out − Th ,in
Tc .in − Th ,in
=
=
68.
40º C − 80º C
= 0,67
20º C − 80º C
20 º C − 50º C
= 0,75
40º C − 80 º C
Entonces, de la Figura 2A del anexo, se tiene:
F = 0,91
a) En el caso de que no se tenga incrustación, el coeficiente de transferencia de
calor total U se determina a partir de:
U =
[
1
1
=
= 21,6 W 2
1 1
1
1
m −º C
+
+
hi h0 160 W 2
25 W 2
m −º C
m −º C
[
] [
]
]
Entonces la velocidad de la transferencia de calor producto de este
aprovechamiento ambiental queda:
[ m −º C]⋅ 3,77[m ]⋅ 0,91⋅ 24,7º C
Q = U ⋅ As ⋅ F ⋅ ∆Tml , CF = 21,6 W
2
2
Q = 1830 [W ]
b) Cuando se tiene incrustación sobre una de las superficies, el coeficiente de
transferencia de calor total U es:
U =
[
1
1
=
= 21,3 W 2
2
1 1
1
1
m −º C
+ + Rf
+
+ 0,0006 m − º C
W
W
W
hi h0
160
25
m2 −º C
m2 −º C
[
] [
]
[
]
]
Entonces la velocidad de la transferencia de calor producto de este
aprovechamiento ambiental queda:
[ m −º C]⋅ 3,77[m ]⋅ 0,91⋅ 24,7º C
Q = U ⋅ As ⋅ F ⋅ ∆Tml , CF = 21,3 W
2
2
Q = 1805 [W ]
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
Nótese que la velocidad de la transferencia de calor d
69.
rece como resultado de la
incrustación, como era de esperarse. Sin embargo, la disminución no es
aplastante debido a los más o menos bajos coeficientes de transferencia de calor
por convección que intervienen.
Consideremos ahora los siguientes datos para la glicerina y el agua:
cp,glicerina = 0,58 kcal/kg - °C
cp,agua = 0,999 kcal/kg - °C
Determinemos qué flujo de agua requerimos para transferir el calor deseado y qué
flujo de glicerina podemos calentar:
Q = 1830W
Sabemos que:
Y además:
(
) ⋅ (T
) ⋅ (T
Qagua = F ⋅ c p
(
Qglicerina = F ⋅ c p
agua
glicerina
agua, out
− Tagua ,in
glicerina, out
) (Q < 0 _(calor _ transferido))
) (Q
> 0 _(calor _ absorbido) )
agua
− T glicerina,in
glicerina
Hallando los flujos antes mencionados, se tiene:
Fglicerina =
Qglicerina
=
c p ,glicerina ⋅ (Tglicerina,out − Tglicerina ,in )
1830[W ]
1[J ]
×
0,58cal
× (50°C − 20°C )
 kg − °C  0,2389[cal]
Por lo que, el flujo obtenido de glicerina es:
Fglicerina = 25,13 kg 
 s 
Para el agua:
Fagua =
(
Qagua
c p ,agua ⋅ T agua,out − T agua,in
=
)
− 1830 [W ]
1[J ]
×
0,999 cal
× (40 °C − 80 °C )
 kg − °C  0,2389 [cal ]
Por lo tanto el flujo de agua aprovechada ambientalmente es:
Fagua = 10,94 kg 
 s 
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
70.
CAPÍTULO VI
HUMIDIFICACIÓN, S ECADO Y COMBUS TIÓN
6.1. Impo rtancia
La importancia de este capítulo a la problemática ambiental radica de acuerdo a
su aplicación; así la humificación permite enriquecer de humedad a un gas, el cual
es importante porque podemos controlar la humedad del aire en ambientes
cerrados, en el caso de lugares de serranía como es sabido son lugares de baja
humedad y este tema es un potencial a considerar, como ejemplo los hoteles
puedes ofrecer a sus huéspedes ambientes no sólo tempe ados sino también con
la humedad del caso; otro caso es cuando se tiene un ambiente contaminado con
partículas en suspensión, se puede adicionar al mismo umedad para dar más
peso a las partículas y hacer que estos por gravedad precipiten y se evite la
afectación
a las
vías
respiratorias.
En cuanto al
aprovechamiento del calor a fin de extraer humedad de
secado estudia
el
s cuerpos sólidos para
fines diversos como mayor duración de productos perecibles o para ocupar
menos espacio, etc.; en el campo ambiental por ejemplo se utiliza para secar los
lodos producidos de la planta de tratamiento de aguas residuales y muchas veces
estos lodos secos dependiendo del tipo de agua residua son utilizadas como
abono, lo cual el secado contribuye a la reutilización de lodos y evita que los
mismos ocupen espacios innecesarios. Finalmente, la combustión basa su
estudio en la química de los combustibles con respecto al oxígeno a fin de
aprovechar su energía y al mismo tiempo para minimizar gases de combustión
especialmente del tipo tóxica y a la vez aprovechar esta energía en diversas
actividades del hombre entre ellos la pausterización, en el campo ambiental la
combustión es un problema pues produce problemas ambie tales y al mismo
tiempo es una solución, ello va a depender de su aplicación, así si se aplica para
generar energía a partir de combustibles crea problemas ambientales como efecto
invernadero, pero si se utiliza para eliminar cuerpos
grosos bajo control es una
solución porque evita que estos cuerpos ocupen espacio y por lixiviación
contaminen cuerpos receptores, tal es caso de cadáveres o gases de metano
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
71.
generado en rellenos sanitarios, si no son quemados es os gases de metano
(CH4) calienta la Tierra 23 veces más que la misma masa de gas carbónico (CO2)
que producido en la combustión y es a este último gas al que la ciencia le atribuye
la responsabilidad del calentamiento global de la Tierra.
6.2. Es tudio
En este capítulo se estudiará tres temas, cuyos ítems son:
• Humidificación y deshumificación.
• Secado.
• Combustión y pasteurización.
6.3. Humidific ac ió n y de s humific ac ió n
Definición: La humidificación es la operación de aumentar la humedad de un gas,
basa su estudio en aprovechar el aire húmedo o el vapor de agua para enriquecer
otros gases de humedad con fines ambientales. Así, la humidificación está
basado en mezclas de vapor de agua y gases, siendo el
ás conocido con
mezcla de aire, en cambio la deshumificación es lo contrario. Para este estudio en
base a Nakamura (1982), las ecuaciones físico-químicas utilizadas son las
siguientes:
a) Fracción Mo lar:
Para gases la fracción molar es la proporción de moles o de presiones la de la
parcial entre el total.
y=
n
n
v
=
T
x=
n
n
g
T
=
P
V
P
(6.1.)
Pg
P
(6.2.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
72.
b) Pres ión to tal
Es la suma de las presiones parciales.
P = Pg + Pv
(6.3.)
También, la presión absoluta (Pa) es igual a la suma de las presiones
manométrica (Pman) y atmosférica (Patm), cuya ecuación es:
Pa = Pman + Patm
(6.4.)
Para efectos de evaluación de gases, tal es el caso del aire requerido para la
combustión, se sugiere utilizar la ecuación universal siguiente:
P.V. = n.R.T.Z
(6.5.)
Que es una ecuación con origen en los gases ideales, cuyas variables son:
Presión (P), volumen (V), número de moles (n), constan e de los gases ideales
(R), temperatura (T) y factor de compresibilidad (Z).
c) Entalpía es pecífica:
La entalpía específica (i) está definida en función de calor específico (c),
temperatura (t), calor latente (?) y humedad (Y).
i = c(t − t o ) + l o Y
(6.6.)
Para el caso aire-agua, a 0ºC se utiliza:
i = (0, 24 + 0,46Y )t + 597 ,2Y
(6.6.1.)
Aquí “t” en ºC y la unidades de “i” Kcal/Kg.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
73.
6.3.1. Es tudio de hu mificació n
A) Diagrama Ps icro métrico
Para la lectura de propiedades de humificación se utiliza los diagramas
psicrométricos, la lectura se basa tomando en cuenta líneas o curvas, cuyas
variables son:
f
= humedad relativa
To =
peratura de operación.
Ts = Temperatura de saturación
Tr = Tem
ratura de rocío.
Tw = Temperatura del bulbo húmedo.
Y = Humedad absoluta.
Estas variables se muestran en la Figura Nº Ap 1., que está en el apéndice de
este texto.
B) Técnicas de humificac ió n
Las más utilizadas son:
a) Mezclas de dos masas de gases húmedas.
b) Por adición de vapor saturado.
Desarrollando cada una de las mencionadas, se tiene:
a) Mezclas de dos mas as de g as es húmedas :
Es una técnica importante porque permite tomar dos flujos húmedos para producir
otro de acuerdo al interés; así se puede aprovechar la humedad de una corriente
de aire procesado para obtener un ambiente adecuado, que muy bien podría ser
utilizado en ambientes por ejemplo de baja humedad.
Partiendo de la Figura Nº 6.1. y, haciendo los balances de masa y energía resulta:
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
Y =
i=
G1.Y 1 + G 2.Y 2
G1 + G 2
74.
(6.7.)
G1.i1 + G2.i 2
G1 + G2
(6.8.)
G
G1
Y1
HUMIFICADOR
Y
G2
Y2
Fig ura Nº 6.1.: Humificac ión mezcla
t=
G1.t1 + G 2.t 2
G1 + G2
(6.9.)
Las ecuaciones (6.8.) y (6.9.), se obtienen siguiendo el patrón de la ecuación
(6.7.), cuyos modelos obtenidos se basan en el modelo empírico; de igual forma
se ilustra la ecuación (6.10.).
Y − Y1 Y − Y 2
=
i − i1
i − i2
(6.10.)
b) Por adició n de vapo r s aturado
Esta es otra técnica importante, dado que ilustra que
podemos aumentar su humedad al añadir vapor de agua, c
corrientes de aire
lo que se puede
mejorar la humedad de cualquier ambiente.
Considerando la Figura Nº 6.2, y realizando balances de masa y energía resulta:
Y 1.G + mV = Y .G
(6.11.)
De la ecuación (6.11.), mV es la masa de vapor añadido y G la velocidad másica
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
75.
del aire húmedo.
Para la entalpía específica, de igual manera se considera la entalpía del aire
húmedo y del vapor utilizado, cuyo balance resulta:
i = i1 + iV ( Y − Y 1 )
(6.12.)
G
Y
HUMIFICADOR
mV
G
Y1
Figura Nº 6.2.: Humific ado r por adic ión de vapor
6.3.2. Humific ació n adiabática
Su estudio se divide por transporte de materia o de calor y cada caso su estudio
es:
a) En bas e al trans po rte de mate ria:
Se aplica los siguientes modelos:
Hy =
G
Ky .a
Ny = ln
Yw − Yo
Yw − Y 3
(6.13.)
(6.14.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
Z = Ny
G
Ky.a
(6.15.)
V = Ny
Wg
Ky.a
(6.16.)
76.
De estos modelos sus variables corresponden Hy (altura del elemento de
transmisión), Ny (número de elementos de transmisión), Z (altura de la torre), V
(volumen de la torre), G (velocidad másica), Ky (coefi
de transporte de
materia), Wg (flujo de masa del aire), Yw (humedad saturado del aire a la salida
del humificador), Yo (humedad del aire a la entrada de precalentador).
b) En bas e al trans po rte de calo r:
Se aplica los siguientes modelos:
Ht =
G.c
hc.a
(6.17.)
Nt = ln
t1 − tw
t 2 − tw
(6.18.)
Z = Nt
G.c
hc.a
(6.19.)
V = Nt
Wg.c
hc.a
(6.20.)
Ht =
Z
Nt
(6.21.)
De estos modelos sus variables corresponden Ht (altura del elemento de
transmisión), Nt (número de elementos de transmisión), Z (altura de la torre), V
(volumen de la torre), G (velocidad másica), hc (coeficiente de convección aireagua), Wg (flujo de masa del aire), tw (temperatura del aire a la salida del
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
77.
humificador), t1 (temperatura del aire a la salida del precalentador), t2
(temperatura del aire a la salida del humificador), c
condiciones medias entre la entrada y salida del humif
r específico del aire en las
dor), a (área de contacto
por unidad de volumen del humificador).
6.4. S e c ado
Definición: El secado como su nombre lo indica, es una operación de eliminar
humedad de un sólido, pero no totalmente, su diagrama de operación se ilustra en
la Figura Nº Ap. 2., que se muestra en el apéndice de este texto.
6.4.1. Anális is de s ec ado
En toda operación de secado, la curva del mismo es conforme lo mostrado en la
Figura Nº Ap.2. del apéndice y, tomando en cuenta dicha figura se cumple, que el
tiempo total (?t) es igual al tiempo variable (?v) más el tiempo constante (?c), así
se tiene:
q t = qv + qc
(6.22.)
qc =
Ls Xi − Xc
.
A
Nc
(6.23.)
qv =
Ls Xc − Xf
Nc
.
ln
A Nc − Nf
Nf
(6.24.)
De las ecuaciones (6.23.) y (6.24.), las variables Ls, A, X y N corresponden al
flujo másico del sólido a secar, superficie de secado,
velocidad de secado.
centración de humedad y
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
78.
6.4.2. Tipo s de s ecado res
Los tipos de secadores son:
a) Secadores lineales.
b) Secadores rotatorios.
El estudio de cada tipo comprende:
A) S ecado res lineales
Son secadores cuya representación se muestra en la Fig
G
6.3.:
G
Y1
SECADOR
Y2
Ls
Ls
X2
X1
Figura Nº 6.3.: S e c ador line al
De la Figura Nº 6.3., efectuando balance de masa tomando en cuenta el siguiente
criterio:
Humedad ganada = Humedad perdida.
Resulta:
G (Y 2 − Y 1) = Ls .( X 1 − X 2 )
(6.25.)
B) S ecado r rotato rio
B.1. De finició n y clas ificació n :
Son equipos cilíndricos cuya función de secado es girando sobre su eje y pueden
ser a secado en flujo contracorriente o a flujo concur nte, en relación a su diseño
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
79.
el volumen de estos secadores deberá ser ocupado por la carga de sólidos del 3
al 10 %. Para determinar el flujo de aire requerido y el tipo de ventilador para su
transporte, se aconseja utilizar las figuras 4A y 5A del anexo.
Estos equipos Forman un grupo muy importante de secadores; son adecu dos
para manejar materiales granulares de flujo libre que pueden arrojarse sin temor
de romperlos. En la Figura 6.5. se muestra uno de estos secadores, un secador
de aire caliente directo a contracorriente. El sólido
secar se introduce
continuamente en uno de los extremos de un cilindro giratorio, como se muestra,
mientras que el aire caliente fluye por el otro extremo. El cilindro está instalado en
un pequeño ángulo con respecto a la horizontal; en con ecuencia, el sólido se
mueve lentamente a través del aparato. Dentro del seca or, unos elevadores que
se extienden desde las paredes del cilindro en la longitud total del secador
levantan el sólido y lo riegan en una cortina móvil a través del aire; así lo exponen
completamente a la acción secadora del gas. Esta acció
elevadora también
contribuye al movimiento hacia adelante del sólido. En el extremo de alimentación
del sólido, unos cuantos elevadores espirales pequeños ayudan a impartir el
movimiento inicial del sólido hacia adelante, antes de que este llegue a los
elevadores principales. Es obvio que el sólido no debe ser pegajoso ni chicloso,
puesto que podría pegarse a las paredes del secador o
En estos casos, la recirculación de una parte del prod
ndería a apelotonarse.
o seco puede permitir el
uso de un secador rotatorio.
El secador puede alimentarse con gas de combustible caliente y no con aire;
además, si el gas sale del secador a una temperatura lo suficientemente alta, al
ser descargado a través de un montón de aire puede pro orcionar una corriente
de aire natural adecuada que proporcione el gas suficiente para el secado. Sin
embargo, de ordinario, se utiliza un ventilador de extracción para jalar el gas a
través del secador, porque así se obtiene un control m
completo del flujo de
gas. Se puede interponer un recolector de polvo, del t po de ciclón, filtro o de
lavado entre el ventilador y el gas saliente.
También puede ponerse un ventilador de empuje en la entrada del gas; de esta
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
80.
forma se mantiene una presión cercana a la atmosférica en el secador; éste
previene la fuga de aire frío en los extremos de almac namiento del secador; si la
presi6n está bien balanceada, la fuga hacia el exterio también puede reducirse al
mínimo. Los secadores rotatorios se fabrican para diversas operaciones. La
clasificaci6n siguiente incluye los tipos principales.
1. Calo r directo , flujo a co ntraco rriente. Para materiales que pueden calentarse
a temperaturas elevadas, como minerales, arena, piedra caliza, arcillas, etc., se
puede utilizar un gas de combustible como gas de secad . Para sustancias que
no pueden calentarse excesivamente, como ciertos productos químicos cristalinos
como sulfato de amonio y azúcar de caña, se puede utilizar aire caliente. El
arreglo general es el que se muestra en la Figura 6.4.; si se utiliza gas de
combustible, las espirales de calentamiento se reemplazan por una caldera que
esta quemando gas, aceite o carbón.
Figura Nº 6.4. : S e c ador de aire c alie nte de Rag gle s -Co le s XW, fabric ado por
Hardinge Co. Inc .
Fuente: Perry y Chilton (1990)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
81.
2. Calo r directo , flujo a co rriente paralela. Los sólidos que pueden secarse con
un gas de combustible sin miedo de contaminarlos, pero que no deben calentarse
a temperaturas muy elevadas por temor a dañarlos (como yeso, piritas de fierro, y
materiales orgánicos como la turba y la alfalfa), debe secarse en un secador con
flujo a corriente paralela. La construcción general es muy similar a la de la Figura
6.4, excepto en que el gas y el sólido entran por el mism
mo del secador.
3. Calo r indirecto , flujo a contraco rriente. Para sólidos como pigmentos
blancos y similares, que pueden calentarse a temperaturas elevadas pero que
nunca deben entrar en contacto con el gas, puede utili
el secador indirecto
que se muestra en forma esquemática en la Figura 6.5. a. Como una construcción
alternativa, el secado puede encerrarse en una estructura de ladrillo y rodearse
completamente con los gases calientes de combustible.
flujo de aire en un
secador de este tipo debe ser mínimo, puesto que el calor se proporciona por
conducción a través de la estructura o tubería central; además, de esta manera
pueden manejarse los sólidos muy finamente divididos q
polvo. Para los sólidos que no se deben calentar a tem
tienden a formar
raturas elevadas y para
los cuales es deseable el calor indirecto, como el alimento para ganado, granos
para cerveza, plumas y similares, se puede utilizar el secador de tubería con
vapor que se muestra en la figura 6.5. b. El secador puede tener o no elevadores
y puede construirse con una, dos o mas hileras concént
s de tubos calentados
con vapor. Como los tubos giran con el secador, es necesaria una junt
toria
especial en donde se introduce el vapor y se separa el condensado. Con
frecuencia se utiliza este tipo de secador cuando se necesita la recuperación del
líquido evaporado.
4. Dire cto-indirecto . Estos secadores, más económicos de manejar que los
secadores directos, pueden utilizarse para sólidos que pueden secarse a altas
temperaturas mediante un gas de combustible, en especial cuando los costos de
combustible son altos y cuando se deben eliminar elevados porcentajes de
humedad del sólido. En la Figura 6.5. se muestra un arreglo típico. En un secador
de este tipo, el gas caliente puede entrar al tubo cen ral a 650 a 980 “C (1 200 a 1
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
82.
800 º F), ser enfriado hasta 200 a 480 ºC cuando pase por primera vez por el
secador y ser regresado a través del espacio de secado anular para que se enfríe
más aún hasta 60 a 70 ºC durante la descarga. La lignita, carbón y coque pueden
secarse en atmósfera inerte en este secador a temperat as relativamente altas
sin peligro de que se quemen o de provocar una explosi
de polvos.
El secador S olid aire contiene gran número de paletas unidas a un eje axial, que
se extienden hasta cerca del interior de la cubierta.
s paletas giran a una
velocidad relativamente alta, 10 a 20 m/s (2 000 a 4 000 ft/min); la fuerza
centrífuga impartida de esta manera a los sólidos los mantiene en contacto con la
cubierta caliente. El gas caliente que fluye a corriente paralela con respecto a los
sólidos les imparte su movimiento hacia adelante.
Se ha demostrado que la insonación de alta frecuencia umenta sustancialmente
la rapidez de secado en los secadores rotatorios. Aunque son distintos los
fabricantes que construyen todos estos secadores, éstos se consiguen en
tamaños estándar, que van desde 1 m de diámetro por 4 m de longitud hasta 3 m
de diámetro por 30 m de longitud.
B.2. Mode lo s matemático s para s ecado res ro tato rio s
Los modelos matemáticos básicos son los siguientes:
q =
0,35 L
s. N
0, 9
.D
± 0,6
B.L.Gv
Gf
(6.26.)
De la ecuación (6.26.), corresponde al tiempo de secado (?), cuyos signos ± se
utilizan según el tipo de secado rotatorio y significan:
+ : Para secado a flujo contracorriente.
-
: Para secado a flujo concurrente.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
Para determinar el calor requerido (Q) para este secad
Q = Ua.V .∆T
83.
utiliza:
(6.27.)
A su vez las variables de la ecuación (6.16.) sus expresiones son:
∆T = T 2 − T 1
(6.28.)
De la ecuación (6.17.), Tanto T1 y T2, corresponde a la temperatura de ingreso y
salida del aire en el equipo.
El Coeficiente Global de transferencia de calor, es determinado por la ecuación de
Friedman y Marshall:
0 ,16
Ua = 0,63 Gv (Gf + B.Gv.r b)
D
Donde:
B = 5, 2 ( Dp )
0 ,5
(6.29.)
−0, 5
(6.30.)
Por otro lado, la velocidad (Vt) del aire en el equipo de secado son determinados
por los siguientes modelos:
Vt =
( r s − r ).g . Dp
2
18 m
(6.31.)
En cuanto a velocidad másica (Gv):
Gv =
Vt.P.M
R.T .Z
(6.32.)
Es importante evaluar para esta dinámica el Número de eynold (Re):
Re =
r .Vt.Dp
m
(6.33.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
84.
Figura Nº 6.5 : Algunos s e c adore s ro tatorios (e s que mátic o )
Fuente: Perry y Chilton (1990).
6.5. Combus tió n y pas te urizac ió n
6.5.1. Co mbus tión
Definición: Mackenzie y Masten (2004), enfatizan que la combustió
es una
reacción química en la cual generalmente se desprende na gran cantidad de
calor y luz. Por eso, es una reacción exotérmica en donde participan tres
elementos: Combustible, oxígeno y activador; el elemento que arde se denomina
(combustible) y otro que produce la combustión (comburente), generalmente
oxígeno en forma de O2 gaseoso.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
85.
El oxígeno para la combustión normalmente se utiliza directamente del aire n la
que está presente en una proporción del 21 % y, el act
para la combustión
con frecuencia es la chispa de un fósforo u otra forma que puede ser un
cortocircuito, etc.
Los explosivos tienen oxígeno ligado químicamente por lo que no necesitan el
oxígeno del aire para realizar la combustión.
El combustible es cualquier sustancia que contenga car
no a excepción del
dióxido de carbono por estar saturado de oxidación. Lo tipos más frecuentes de
combustible son los materiales orgánicos que contienen carbono e hidrógeno. En
una reacción completa todos los elementos tienen el mayor estado de oxidación.
Los productos que se forman son el dióxido de carbono CO2) y el agua, el dióxido
de azufre (SO2) (si el combustible contiene azufre) y pueden aparecer
idos de
nitrógeno (NOx), dependiendo de la temperatura de reacción.
En la combustión incompleta los productos que se queman pueden no reaccionar
con el mayor estado de oxidación, debido a que el comburente y el combustible
no están en la proporción adecuada, dando como resulta
compuestos como el
monóxido de carbono (CO). Además, pueden generarse cenizas.
El proceso de destruir materiales por combustión se co
como incineración.
Para iniciar la combustión de cualquier combustible, es necesario alcanzar una
temperatura mínima, llamada temperatura de ignición, q
se define como, en ºC
y a 1 atm, temperatura a la que los vapores de un comb stible arden
espontáneamente.
La temperatura de inflamación, en ºC y a 1 atm es aquella que, una vez
encendidos los vapores del combustible, éstos continúa
por si mismos el
proceso de combustión.
La reacción del combustible con el oxígeno origina sus ancias gaseosas entre las
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
86.
cuales las más comunes son CO2 y H2O. Se denominan en forma genérica
productos, humos o gases de combustión. Es importante
stacar que el
combustible solo reacciona con el oxigeno y no con el
geno, el otro
componente del aire. Por lo tanto el nitrógeno del air pasará íntegramente a los
productos de combustión sin reaccionar.
Entre las sustancias más comunes que se pueden encontrar en los productos o
humos de la reacción se encuentran:
CO2
H2O como vapor de agua
N2
O2
CO
H2
Carbono en forma de hollín
SO2
La reacción más frecuente de la combustión es como se muestra a continuación y
puede ser completa e incompleta, así tenemos:
Combustible + Aire
?
Combustible + Aire ?
Dióxido de carbono
+ agua
(C. C).
Monóxido de carbono + agua
(C. I.).
Leyenda: (C.C.) = Combustión completa.
(C.I.) = Combustión incompleta.
En ambas reacciones se desprende energía, naturalmente
obtiene mayor
energía en la reacción completa. De ahí la importancia de producir una
combustión completa, pues maximiza el uso del combusti
y minimiza las
pérdidas, a parte que no es contaminante al ambiente, lo único negativo que
incrementa el efecto invernadero de la atmósfera, cuyas consecuencias entre
ellas está la perdida de agua dulce por eliminación de nevados, incremento de
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
87.
altura de los mares, etc.
TABLA Nº 02: CALIDAD PROMEDIO DE COMBUS TIBLES
COMBUSTIBLE
API
Gasolina 95 octanos
80
Gasolina 95 octanos
75
Gasolina 84 octanos
67,4
Nafta
55,0
Turbo
44,4
Kero
40,1
Diesel
33,3
Residual Nº 6
19,1
Fuente: PETROPERU (2000)
En la práctica, no se debería continuar obteniendo energía a partir de la
combustión, sino a través de otras formas como son el
renovables entre ellas la eólica, solar, etc. Sin emba
so de energías
aún nuestro sistema
continuará quemando combustibles dado que la tecnología que usamos la
demanda. Por eso, es imperioso la necesidad de ir cambiando este modelo por el
bien de la humanidad.
Para conocer los calores específicos (Qe) de los combu
les más utilizados, a
continuación se detallan:
1.- Para Diesel:
Qe = 9823 + 33,34 x ºAPI
(cal/kg)
(6.34.)
2.- Para Aceites combustibles:
Qe = 10140 + 22,22 (Bé-10)
(cal/kg)
(6.35.)
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
88.
3.- Para Carbón mineral:
Qe = 145,44 C + 620 (H - O/8) + 41 S
(BTU/lb)
(6.36.)
4.- Para Bunker o fuel oil o crudo:
To
T 

Qe = 0,975VCS + (h − ho) 1 −
ln 
 T − To To 
(kcal/kg)
(6.37.)
5.- Para Gases combustibles (fuel gas):
Qe = 0,950 VCS + R.To lnP/Po
(kcal/kg)
(6.38.)
6.5.2. Pas teurización
Definición: ADAMS (2010), sostiene que la pasteurización es una o
eliminación de microorganismos patógenos en líquidos,
ración de
lo cual se utiliza
calor como medio de acción; ejemplo de ello es la pasteurización de la leche en
autoclaves, en donde se acciona utilizando vapor de ag
como medio calefactor.
En otros casos, se utiliza los gases de combustión. El más utilizado es el vapor de
agua a nivel industrial. La pasteurización es necesari realizar antes de envasar
cualquier alimento líquido, como medio calefactor se utiliza intercambiadores de
calor los cuales han sido antes estudiados en este tex o.
Diferenc ias entre pas teurización y es terilizació n: La pas teurización es el
término aplicado al proceso que se utiliza para la destrucción de algunos de los
microorganismos posiblemente presentes en materiales sensibles al calor como la
leche y cerveza. Consiste en calentar la leche, por ejemplo a 62 °C, mantenerla a
esta temperatura 30 minutos y después enfriarla lo más rápidamente posible. Esta
técnica no es de ninguna manera un procedimiento de esterilización. Es
solamente un método para destruir organismos patógenos y al mismo tiempo
disminuir el nivel de aquellos organismos que más pueden deteriorar la leche.
La e s terilización significa la eliminación de toda forma de vida de un m dio o
material, lo que se lleva a cabo generalmente por medios físicos, por ejemplo,
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
filtración, o por muerte de los organismos por calor,
89.
oductos químicos u otra vía.
Esta definición excluye por lo tanto cualquier técnica que resulte solamente en un
daño a los microorganismos o atenuación de la actividad de cualquier tipo.
Por otro lado, la pasterización o Tecnología de Proceso de Pasteurización, recibe
su nombre de Louis Pasteur, un químico / microbiólogo Francés, que
scubrió
que los organismos que causan la descomposición pueden ser desactivados en el
vino aplicando calor a temperaturas por debajo de su p nto de ebullición. En
realidad, solo necesitó calentar el vino a 55 °C por unos pocos minutos para matar
los microorganismos que causaban que el vino se arruinara. El proceso se aplicó
posteriormente a la cerveza y la leche (y muchos otros roductos) y sigue siendo
una de las operaciones más importantes que se realizan en las instalaciones de
procesamiento de alimentos, lácteos y bebidas.
La pasteurización puede ser continua o por lotes, con especto a la continua tiene
varias ventajas por encima del método de pasteurizació
or lotes (VAT), siendo
la más importante el ahorro de tiempo y energía. Para la mayoría de l s
procesamientos continuos, se utiliza un pasteurizador
tiempo breve a alta
temperatura (high temperature short time / HTST). El t atamiento de calor se lleva
a cabo utilizando ya bien un intercambiador de calor a placas (PHE) o un
intercambiador de calor tubular. El intercambiador a p acas consiste de una pila
de placas de acero inoxidable corrugado prensadas dent
de un marco. Hay
varios patrones de flujo que pueden ser utilizados. Se utilizan empaques para
definir las fronteras de los canales y evitar fugas. El medio de calentamiento es
normalmente vapor o agua caliente. Los intercambiadore de calor tubulares se
utilizan cuando los fluidos contienen partículas que bloquearían los canales de un
intercambiador de calor a placas.
También se utiliza la Ultrapasteurización (UP) que es n proceso similar a la
pasteurización HTST, pero utilizando equipo ligeramente diferente, temperaturas
más altas y tiempos más prolongados. La pasteurización UP resulta en un
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
90.
producto con vida útil más prolongada pero que aún req
de refrigeración.
Otro método, la esterilización Ultra High Temperature
(Temperatura
Ultraelevada) eleva la temperatura de la leche a por lo menos 280° F durante dos
segundos, seguido de un rápido enfriamiento.
La leche pasteurizada UHT empacada de forma aséptica r sulta en un producto
"de vida de anaquel estable" que no requiere de refrigeración hasta que se abre.
Un sistema de pasteurización normalmente contiene los siguientes componentes:
•
Tanque de balance con conjunto de válvula de flotación
•
Regenerador
•
Homogenizador de alta presión
•
Bomba de desplazamiento positivo equipada con un varia
velocidad
o una bomba centrífuga con medidor de flujo magnético controlador
•
Tubo de sostenimiento
•
Registrador-controlador
•
Dispositivo de desviación de flujo
•
Rompedor de vacío
•
Separador (clarificador)
Finalmente se usa la Pasteurización Flash, la misma que funciona al calentar
rápidamente una bebida a una temperatura de alrededor de 160 -180 ºF antes del
proceso de llenado y tapado. La bebida será conservada a esta temperatura por
menos de 20 segundos antes de ser rápidamente enfriada utilizando otro
intercambiador de calor. Este proceso aporta varias ve
s de espacio y costo
debido a la manipulación de la bebida en lote antes del ll nado. La desventaja de
la pasteurización flash en comparación con la pasteurización de túnel consiste en
que requiere de un llenado estéril y de contenedores e
riles. Mantener los
contenedores y el sistema de llenado estériles es complejo, difícil y car
En
comparación, los procesos de pasteurización en túnel conservan la bebida en un
contenedor sellado, evitando así los problemas de contaminación y garantizar una
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
91.
vida útil más larga. En consecuencia, la mayoría de las botellas y latas de cerveza
se pasteurizan en pasteurizadores de túnel.
TABLA Nº 03: PAS TEURIZACIÓN DE LÁCTEOS
TEMPERATURA
TIEMPO
63°C (145°F)
30 minutos
TIPO DE
PAS TEURIZACIÓN
Pasteurización VAT
Pasteurización "High
72°C (161°F)
15 segundos
temperature short time
Pasteurization" (HTST)
89ºC (191ºF)
1.0 segundo
Ultra Pasteurización (UP)
90ºC (194ºF)
0.5 segundos
Ultra Pasteurización (UP)
94ºC (201ºF)
0.1 segundos
Ultra Pasteurización (UP)
96ºC (204ºF)
0.05 segundos
Ultra Pasteurización (UP)
100ºC (212ºF)
0.01 segundos
Ultra Pasteurización (UP)
138ºC (280ºF)
2.0 segundos
Esterilización Ultra-high
temperature (UHT)
Fuente: http://www.idfa.org/facts/milk/pasteur.cfm.
PROBLEMAS APLICATIVOS
PROBLEMA 6.1. (Aplicación de humificac ió n)
Los ambientes de un hotel contienen 1000 m3 de aire a 25 ºC con una humedad
de 0,009 Kg de agua/Kg de aire, lo cual requiere humificar para el confort de sus
clientes y para ello adiciona vapor de agua saturado a 1 atm en cantidad tal que la
humedad final obtenida después de la adición de vapor de agua sea 0,02 Kg de
agua/Kg de aire. Si la homogenización de la mezcla es
al sin condensación
sobre las paredes y despreciando las pérdidas de calor determinar:
a) Cantidad de vapor de agua adicionada.
b) Temperatura final del sistema.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
92.
S OLUCIÓN:
a) El volumen específico del aire determinado en la gráfi
psicrométrica a 25 ºC y
3
0,009 Kg de agua/ Kg de aire es 0,855 m /Kg. Entonces la masa de aire seco
será: 1000 m3 / 0,855 m3 /Kg = 1169 Kg.
Calculando masa de vapor adicionado:
Mv = G (Y – Y1) = 1169 (0,02 -0,009) = 12,86 Kg.
Lo que quiere decir que los ambientes del hotel requiere 12,86 Kg de vapor para
condicionar su humedad.
b) Determinando la entalpía del vapor saturado a 1 atm:
Por tablas de vapor de agua corresponde a: iv = 638,5 Kcal/Kg.
Hallando la entalpía del aire húmedo en las condicione niciales:
Por fórmula dada en este capítulo: i1 = (0,24 + 0,45 Y1)t + 597,2 . Y1,
reemplazándola se tiene:
i1 = (0,24 + 0,46 . 0,009)25 + 547,2 . 0,009 = 11,47 Kcal/Kg.
Luego la entalpía total es:
i = i1 + iv (Y – Y1) = 11,47 + 638,5 (0,02 – 0,009) = 18,49 Kcal/Kg.
Aplicando el modelo de entalpía del aire húmedo se tiene:
i = (0,24 + 0,45 Y1)t + 597,2 . Y ……………. (a),
De donde “ t “ es la pregunta
e
i = 18,49 Kcal/Kg ,
así como Y = 0,02 Kg de agua/ Kg de aire
Reemplazando la ecuación (a), se obtiene: t = 26, 3ºC.
Entonces para lograr un aire humificado para los ambientes del hotel en las
condiciones solicitadas se incrementa el mismo en 1,3 ºC
cual es aceptable.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
93.
PROBLEMA 6.2. (Aplicación de s ecado)
Un secador rotatorio de 5 pies de diámetro y 60 pies d largo, se va a usar para
secar un residuo sólido a contracorriente desde un contenido de humedad de 0,3
lb de agua por libra de sólido seco, hasta una concentración de 0,02 lb de agua.
El residuo tiene un tamaño medio de partícula de 50 micras y una densidad de
240 lb/ft3 . El secador opera a una velocidad de 4 rpm y con una inclinación de 0,5”
cada 10” de longitud. ¿Qué gasto de aire se requiere para el secado?, si el aire en
el secador alcanza la temperatura de 2000 ºR.
S OLUCIÓN:
Aplicando la ecuación (6.22),
Vt =
( r s − r ).g . Dp
2
18 m
Dado que (?s = 240 lb/ft3), (? = 0,05 lb/ft3), (Dp = 50 µ), (g =9,81 m/s2), se
determina la velocidad del aire y es: Vt = 0,860 ft/s,
Que es una velocidad adecuada pues alcanza el Re = 0,5 (ecuación 6.24.) que es
el valor límite para esta operación. Utilizando el valor de Vt y aplicando la
ecuación (6.23.), se determina el valor de Gv que corresponde a 123 lb/h.ft2 , que
es el gasto del aire requerido para secar el residuo sólido solicitado.
PROBLEMAS 6.3. (Aplic ació n de co mbus tión)
El análisis de cierto coque exento de hidrógeno es como sigue: humedad 4,2%;
cenizas 10,3%; carbono 85,5%. El coque se somete a la combustión con lo cual
se obtiene un gas de chimenea seco cuyo análisis es: CO2 13,6%; CO 1,5%; O2
6,5%; N2 78,4%. Asumiendo el factor de comprensibilidad (Z) igual a uno.
Calcular:
(a) Porcentaje de exceso de aire utilizado.
(b) Pies cúbicos de aire a 80 ºF y 740 mm de Hg que en
quemada.
por libra de carbono
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
94.
(c) Lo mismo que en (b) pero por libra de coque quemada.
(d) Pies cúbicos de gas de chimenea seco a 690 ºF / lb de coque.
(e) Pies cúbicos de gas de chimenea húmedo a las condi iones estándar / lb de
coque.
S OLUCIÓN:
Datos del Coque:
Análisis de gases de combustión:
Humedad (H2O)
= 4,2 %
CO2
= 13,6 %
Cenizas
= 10,3 %
CO
= 1,5 %
Carbono (C)
= 85,5 %
O2
= 6,5 %
N2
= 78,4 %
Se toma una base de: 100 moles de gases de combustión
n(CO2)
= 13,6
?
W(CO2)
= 598,4 lb
n(CO)
= 1,5
?
W(CO)
=
n(O2)
= 6,5
?
W(O2)
= 208,0 lb
n(N2)
= 78,4
?
W(N2)
= 2195,2 lb
42,0 lb
Procedemos a hallar el peso total de carbono y de oxígeno (exc ptuando el
oxígeno que entra como parte del agua en la humedad) q e ingreso a partir del
análisis de los gases de combustión:
Hallamos ahora el aire teórico:
C
+
O2
?
CO2
12,0 lb de C
?
32 lb de O2
181,2 lb de C
?
x
x = 483,2 lb de O2
Luego:
2C
+
24,0 lb de C
O2
?
2CO
?
56 lb de CO
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
w
?
95.
42,0 lb de CO
w = 18,0 lb de C
Tenemos que calcular ahora la cantidad de O2 que entra con la humedad:
181,2 lb de C
?
85,5 %
y
?
100,0 %
y = 211,93 lb de coque
Pero la humedad solamente representa el 4,2 % del peso total de coque:
W(Humedad) = 0,042 x 211,93 lb = 8,90 lb de H2O
Y con estos datos ya podemos hallar el porcentaje de exceso de oxígeno y sus
moles:
(a)
V = ? (pies3) del aire.
(b)
T = 80 ºF
P = 740 mm Hg
R = 0,7302 atm x pies3 / mol lb x ºR
Para usar la ecuación universal de los gases solamente nos faltaría conocer el
número de moles del aire / lb de carbono.
181,2 lb de C
?
635,2 lb de O2
1,0 lb de C
?
w
w = 3,51 lb de O2
?
n(O2) = 0,109
Ahora hallamos las moles de O2 que entran / lb de carbono quemado.
V = 210 pies3
(c) Wtotal de coque = 211,93 lb
211,93 lb de coque
?
635,2 lb de O2
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
1,0 lb de coque
a = 2,997 lb O2
96.
?
a
?
n(O2) = 0,094
V = 181,424 pies3
(d)
100 moles de gas chimenea seco
n
?
211,93 lb de coque
?
1,0 lb de coque
n = 0,472 moles de gas de chimenea seco
Aplicando la ecuación universal de los gases (6.5.):
P.V = n.R.T.Z
Y reemplazando en ellas los datos, se tiene:
V = 407,065 pies 3
Lo que significa que la chimenea afecta al medio ambie
con un volumen de
gases secos de combustión de 407,065 pies3.
(e)
100,494 moles de gas chimenea húmedo ?
n
211,93 lb de coque
?
1,0 lb de coque
n = 0,474 moles gas chimenea húmedo
Otra vez, aplicando la ecuación universal de los gases (6.5.):
P.V = n.R.T.Z
Y reemplazando en ellas los datos, se obtiene:
V = 408, 800 pies 3
Lo que significa que la chimenea afecta al medio ambie
con un volumen de
3
gases húmedos de combustión de 408, 800 pies ; el cual se aprecia con respecto
al anterior mayor porque en el valor final considera la humedad.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
97.
PROBLEMA 6.4. (Aplic ación de co mbus tió n)
En una prueba realizada en una caldera con alimentación de aceite no fue posible
medir la cantidad de aceite quemado, aunque el aire que se empleó se determinó
insertando un medidor ventura en la línea de aire. Se ncontró que se había
utilizado 5000 pies3 / min de aire a 80 ºF y 10 lb / plg2 man. El análisis del gas de
chimenea seco es: CO2 10,7%; CO 0,55%; O2 4,75%; N2 84,0%. Si se supone
que el aceite está formado únicamente por hidrocarburos, calcular los centímetros
cúbicos por minuto de aceite que se queman. El peso específico del aceite es
0,94; asumir factor de comprensibilidad (Z) igual a uno.
S OLUCIÓN:
Datos del Aire. Base: 1 minuto.
V = 5000 pies3 ; T = 80 ºF = 540 ºR; Pabs = Pman + Patm = (10 + 14,7) psia = 14,7 psi
Aplicando la ecuación de los gases (6.5.) donde Z = 1, se determina el número de
moles de aire:
Si:
PV = n.R.T.Z, determinamos n del aire de la forma siguiente:
24,7 x 5000 = naire x 10,73 x 540 ?
naire = 21,31
Por lo tanto tendremos también:
n(O2)= 0,21 x 21,31 = 4,475; n(N2) = 0,79 x 21,31 = 16,835
W(O2)= 4,475 x 32 = 143,2 lb; W(N2) = 16,835 x 28 = 471,38 lb
Datos para los gases de combustión secos
CO2
= 10,70 %
CO
= 0,55 %
O2
= 4,75 %
N2
= 84,00 %
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
98.
Aplicando una regla de tres para el N2 que no reacciona tendremos:
ntotales = 16,835 x 100 / 84 = 20,042
Lo que nos daría los siguientes datos:
n(CO2)
= 2,144
?
W(CO2)
= 94,336 lb
n(CO) = 0,110
?
W(CO)
=
n(O2) = 0,952
?
W(O2)
= 30,464 lb
n(N2) = 16,835
?
W(N2)
= 471,380 lb
3,080 lb
Ahora ya sabemos el O2 que se encuentra en el agua.
W(O2)en agua = 143,2 – 100,832 = 42,368 lb
W(H2)en agua = 47,664 x 2 / 16 = 5,296 lb
Este último peso hallado es el H2 que entra con el aceite.
Hallamos ahora el carbono que entra con el aceite.
W(aceite) = 27,048 + 5,296 = 32,344 lb = 14684,176 g
? (aceite) = 0,94 g / cc
Por lo tanto, el volumen de aceite quemado y por tanto impactando el medio
ambiente es:
V = 15621,464 cc / min.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
99.
DIS CUS IÓN DE RES ULTADOS
El presente texto ha sido elaborado cumpliendo con todo el programa del
silabo de la Asignatura de Operaciones Unitarias II de la Facultad de
Ingeniería Ambiental y de Recursos Naturales de la Uni ersidad Nacional del
Callao. El mismo que ha sido desarrollado con enfoque
rico y práctico,
favoreciendo sobre todo la enseñanza-aprendizaje de los estudiantes en la
especialidad de Ingeniería Ambiental.
Por lo que, este texto es un instrumento que facilita
proceso enseñanza-
aprendizaje de la Asignatura de Operaciones Unitarias
impartida
fundamentalmente en la Facultad de Ingeniería Ambiental y Recursos
Naturales de la Universidad Nacional del Callao.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
100.
REFERENCIAS BIBLIOGRÁFÍCAS
1. ADAMS. Pasteurización de lácteos. Leído 12 de Julio de 2010 en
http://www.idfa.org/facts/milk/pasteur.cfm.
2. BIRD BYRON, STEWART WARREN, LIGHFOOT EDWIN. “Fenómenos de
Transporte”. Editorial Reverté S.A. México. 1990.
3. BROWN GEORGE. “Operaciones Básicas en Ingeniería Química”. Editorial
Marín S.A. España. 2003.
4. CHOPEY NICHOLAS y HICKS TYLER. “Manual de Cálculos de
geniería
Química”. Editorial Mc Graw Hill. México. 1995.
5. FELDER, ROUSSEAU. “Principios elementales de los Procesos Químicos”.
3ra edición. Editorial Limusa Wiley. México. 2003.
6. FOUST, WENZEL, CLUMP, MAUS y ANDERSEN. “Principios de
Operaciones Unitarias”. Editorial Continental S.A. México. 1990.
7. GIANKOPLES. “Operaciones Unitarias”. Editorial Mc Graw Hill. México.
1998.
8. HIMMELBLAU DAVID. Principios básicos en Ingeniería Química. Sexta
edición, Editorial Prentice-Hall Hispanoamericana S.A. México. 1998.
9. KERN DONALD. “Procesos de Transferencia de Calor”. Editorial
Continental S.A. México. 2001.
10.KIELY GERARD. “Ingeniería Ambiental”. Editorial Mc Graw Hill. España.
1999.
11.MACKENZIE
DAVIS
y
MASTEN
SUSAN.
“Ingeniería
y
Ciencias
Ambientales”. Editorial Mc Graw Hill. México. 2004.
12.MC CABE SMITH. “Operaciones Unitarias en Ingeniería Química”. Editorial
Limusa. México. 1995.
13.NAKAMURA JORGE. “Termodinámica básica para Ingenieros”. Editorial
Hozlo S.C.R.L. Perú. 1982.
14.OCON/TOJO. “Problemas de Ingeniería Química”. Editoria
Aguilar.
España. 1990.
15.PETROPERU. Refinación de Petróleo. Perú. 2000.
16.PERRY ROBERT y CHILTON CECIL. “Biblioteca del Ingeniero Químico”.
Volumen II. Editorial Mc Graw Hill. México. 1990.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
101.
APÉNDICE
f
Y
= 100 %
f
Ts
T
Tr
Tw
To
Figura Nº Ap 1.: Diagrama Ps ic romé tric o
N
Nc
?v
?c
Nf
X
X
Xc
Figura Nº Ap 2.: Diagrama de s e c ado
X
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
ANEXOS
Figura Nº 1A: Curva de trans fe re nc ia de c alor lado tubo s .
Fuente: Kern Donald (1986).
102.
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
103.
Figura Nº 2A: Fac tor F de te mpe ratura c alóric a.
Fuente: Standards of Tubular Exchanger manufacturers Association, 2ª. Ed., New York,
1949, tomado del Kern Donald (1986).
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
104.
Figura Nº 3A: Fac tore s de c orre c c ión MLDT para tubo-c o raz a 1-2.
Fuente: Standards of Tubular Exchanger manufacturers Association, 2ª. Ed., New York,
1949. Tomado del Kern Donald (1986).
Texto: Operaciones Unitarias II para Ingeniería Ambiental - NJN
Figura Nº 5A: Us os para la e le c c ión de l ve ntilador ade c uado.
Fuente: Perry y Chilton (1990).
105.