1) Tensor de momento sísmico de cizalla pura. El vector de
Anuncio

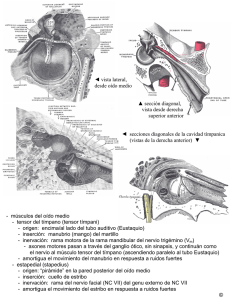
1) Tensor de momento sísmico de cizalla pura. El vector de desplazamiento es paralelo al plano de falla. Se supone una fuente puntual situada en el medio isotrópico. Se trabaja con dos vectores unitarios: en la dirección del desplazamiento y en la dirección perpendicular a la falla (vector de la normal). 2) El tensor expresado en el sistema de coordenadas relacionada con la falla. Tenga en cuenta la presencia de dos componentes idénticas, cada una formada por el producto de la rigidez y el desplazamiento discontínuo ∆u en la falla. El significado físico de este producto es la densidad superficial de momento sísmico. [Si se multiplica la densidad de momento por toda a superficie de falla, S, se obtiene el momento escalar de cizalla pura µ∆u S = Mo.] 5 3) U denomina la onda sismica (desplazamiento) debido a la fuente puntual. La onda depende de dos términos: tensor de momento y tensor de Green. La función de Green corresponde a la acción de una orientación especial: Gip = i-ésima componente de desplazamiento debido a una sola fuerza aplicada a lo largo de p-ésima de coordenadas. Gip,q = derivada espacial de la función de Green. La convolución temporal aparece para expresar el principio de superposición lineal (el campo de ondas, o la reacción, depende de toda la historia de la fuente, o de acción). La suma por p y q para expresar la orientación espacial arbitraria de la falla. [Además, en caso de falla finita tenemos también la integración en el plano de falla.] 4) En nuestro caso sólo dos términos son en efecto: Gi1,3 y Gi3,1. Esto significa que la fuente es equivalente a dos pares de fuerza (es porque se lo llama la fuente de doble par, DC). La fuerza a lo largo del eje 1 tiene el brazo en eje 3, y viceversa. 5) La ecuación para calcular el vector y los valores propios del tensor de momento. 6) En el caso de cizalla pura se tiene un valor propio de cero, y dos valores propios del mismo tamaño y de signo contrario. El símbolo m es la misma densidad superficial de momento, introducida arriba como µ∆u. 6 [Este hecho ya tiene una relacion bien estrecha a practica. Lo que se muestra teoricamente aqui se pude ver cada dia por ejemplo en las soluciones de Global CMT (Harvard) – dos valores del tamano similar y signos opuestos, un valor cerca cero, aunque nunca igual exactamente a cero. La unica diferencia es que en practica no se considera la densidad del moment, sino su integral sobre toda la falla.] 7) Los vectores propios son orinetados a lo largo del eje 2 (vease la figurra anterior) y en 45 grados con respeto a las ejes 1 y 3. Es lo mismo como los ejes B, P y T bien conocidos en los dibujos de la esfera focal - las ejes P y T se encuentran en los centros de los sectores de primeras polaridades negativas y positivas, respectivamente. 7 8) Vamos a representar el mismo campo de ondas como anteriormente, sin embargo, ahora se utiliza el tensor de momento diagonalizado, es decir con sus valores propios en la diagonal. Tenga en cuenta la suma de los términos diagonales = la traza; la traza igual a cero significa deformaciones sin cambio de volumen. Véase tambien que el producto de los términos diagonales = el determinante es igual a cero debido al valor propio de 0, típico para la cizalla pura. La traza y determinante son independientes del sistema de coordenadas, esos son invariantes del tensor de momento. 9) Recuerde que arriba hemos escrito el campo de ondas mediante Gi1,3 y Gi3,1. A base del tensor diagonalizado ahora obtenemos una representación del mismo campo de ondas debido a la misma fuente en forma totalmente diferente: Se puede ver que en el sistema de coordenadas relacionada con los vectores propios los dos terminos jugando el papel son Gi1,1 y Gi3,3 – dos pares de fuerzas, cada par senalandose por fuerzas de la orientacion opuesta, sin brazo. El motivo mayor de esta explicacion fue mostrar que el mismo tensor de momento (la misma quantidad física) puede tener much formas diferentes, que dependen del sistema de coordenadas. 10) En la práctica, si se trabaja en el sistema de coordenadas geograficas NS, EW, Z el tensor de momento suele ser "completo" (o “lleno”). No hay niguna razón para tener solo unos pocos componentes distintos de cero, incluso en el caso especial de cizalla pura. Lo mismo es cierto para el caso de sistema de coordenadas esfericos (como se puede ver en informes de Global CMT). ISOLA expresa el tensor de momento en los ambos sistemas. En otras palabras, para ver la desviacion de cizalla pura no es suficiente ver el tensor en sistemas practicas sino que en el sistema de ejes propios. ISOLA lo hace en forma interna y proporciona el percentaje de volumen (VOL), DC y CLVD. 8 11) Nota: No hemos discutido la funcion de Green, porque su computo en ISOLA tiene forma de ‘black-box’. Sin embargo el usario de ISOLA debe tener en cuenta la complejidad de Gip,q. La mayoria de la complejidaded viene de la heterogenidad del medio (ondas de cuerpo, reflecciones multiples, transformacion de P a S, ondas superficiales, etc). Aqui quisieramos mostrar una complejidad importante que existe incluso en un caso mas simple, eso es en medio infinito homogéneo. De hecho, hablamos sobre los efectos de campo cercano. Estos efectos son de importancia “cerca”de la fuente, es decir hasta una longitud de onda, pero tenga en cuenta que en frecuencia de 0.1Hz esto es la distancia de 30 km (!), lo que quire decir que se pueden encontrar los efects de campo ceracno en practica. ISOLA hace lo possible porque el metodo de DW computa el campo completo de ondas, incluso los terminos especiales de este tipo. En forma esquematica se puede escribir Gip,q como compuesto de tres términos, Gip, q = la derivada de la función delta para P y S + la función delta para P y S + la funcion lineal (trapecio) entre P y S. Entonces, en el caso de M igual al simple paso (Heaviside), tenemos U = M * Gip, q = función delta para P y S + paso para P y S + un pulso cuadrático entre P y S. M =H U = H ∗ G = ∫δ ∗ G = δ ∗ ∫ G = ∫ G 9