CORRIENTE ALTERNA

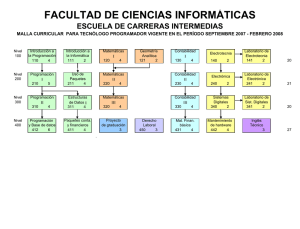
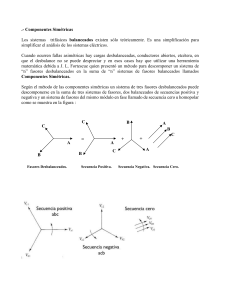
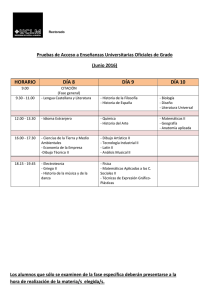
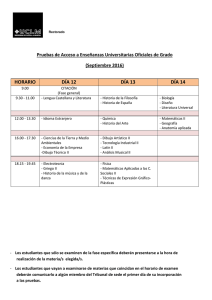
Fasores_Rev2005
1
CORRIENTE ALTERNA - FASORES
Realizado por: Ing. Marcos Deorsola
Editado por : Ing. Guillermo Gastaldi
Revisión 2005 por : Ing. Pablo Morcelle del Valle
FASORES
Las operaciones matemáticas que involucran funciones senoidales se simplifican notablemente mediante el
uso de FASORES.
Un fasor es un numero complejo, cuyas características más importantes se desarrollan a continuación.
En la Fig.(1) se han representado en el plano complejo dos números obviamente complejos U (ϕ) y Ů (ωt+ϕ),
ambos con igual módulo U pero con distinto argumento, para el primero ϕ y para el segundo ϕ mas un ángulo
definido por el producto de la velocidad de giro (del módulo) por el tiempo en que se da ese giro.
El primer complejo, cuyo argumento (fase) es constante, se debe indicar con la nomenclatura propia de los
complejos, es decir con un guión debajo de la letra que identifica al complejo y entre paréntesis el argumento.
En cambio en el caso del segundo complejo el argumento resulta variable dependiendo linealmente del
tiempo, o sea que la posición del punto describe en el plano una circunferencia y el complejo se suele indicar
con un punto encima de la letra además del argumento en función del tiempo entre paréntesis (fase variable).
En consecuencia puede decirse en forma genérica que Ů es un complejo U de fase variable, y que por tal
razón se denomina fasor.
Si se expresa el complejo Ů (ωt+ϕ) por sus componentes real ( Re ) e imaginaria ( Im ) resultan las Ecs.( 1 ):
Uɺ (ωt + ϕ ) = U ⋅ cos(ωt + ϕ ) + j ⋅ U ⋅ sen(ωt + ϕ )
Re(Uɺ (ωt + ϕ )) = U ⋅ cos(ωt + ϕ )
Ecs. (1)
Im(Uɺ (ωt + ϕ )) = U ⋅ sen(ωt + ϕ )
Justamente estas componentes son expresiones senoidales respecto del tiempo y con pulsación idéntica a la
velocidad angular con que se hace girar el número complejo Ů de módulo constante (radio giratorio), siendo
el argumento constante, ϕ, el ángulo de desfasaje de la función senoidal respecto de t=0.
Se presentan a continuación algunas propiedades de los fasores los cuales interesan por el hecho ya marcado
que sus componentes pueden considerarse como tensiones o corrientes senoidales.
a) Un fasor puede expresarse además de la forma cartesiana de la Ec.(1) en la forma polar de la Ec.(2).
Uɺ (ωt + ϕ ) = U ⋅ e j (ωt +ϕ ) = U ⋅ e jωt ⋅ e jϕ
Ec.(2)
b) De la Ec.(2) se distinguen tres componentes:
U : Módulo del fasor.
jωt
e : Fasor ( fase variable ) y módulo unitario.
e jϕ : Complejo de fase constante y módulo unitario.
c) Si se multiplica un fasor por un número real se modifica sólo el módulo del mismo.
Ing. Marcos Deorsola
Prof. Tit de Teoría de Circuitos I y de Electrotecnia y Electrónica
Departamento de Electrotecnia
Facultad de Ingeniería
Universidad Nacional de La Plata
Ing. Pablo Morcelle del Valle
Prof. Adj. de Electrotecnia y Electrónica
Departamento de Electrotecnia
Facultad de Ingeniería
Universidad Nacional de La Plata
Fasores_Rev2005
2
Si en cambio se multiplica un fasor por un número imaginario después del cambio del módulo se produce un
giro de ± π/2 radianes según sea positivo o negativo el número imaginario.
En efecto:
Uɺ (ωt + ϕ ) ⋅ G = U ⋅ e j (ωt +ϕ ) ⋅ G = U ⋅ G ⋅ e j (ωt +ϕ ) = I ⋅ e j (ωt +ϕ ) = Iɺ(ωt + ϕ )
Ec.(3)
Iɺ(ωt + ϕ ) ⋅ j ⋅ X L = I ⋅ e j (ωt +ϕ ) ⋅ X L ⋅ e jπ / 2 = I ⋅ X L ⋅ e j (ωt +ϕ +π / 2 ) =
= U ⋅ e j (ωt +ϕ +π / 2 ) = Uɺ (ωt + ϕ + π / 2)
L
Ec.(4)
L
En las Ecs.(3) se aprecia que la posición de Ů(ωt+ϕ) e Đ(ωt+ϕ) es la misma, mientras que en la Ecs.(4) se ve
que el argumento de UL muestra un adelanto de π/2 respecto del argumento de Đ (ωt+ϕ). En ambos casos los
módulos se han modificado por efecto de G y XL respectivamente.
d) Considerando la suma o resta de varios fasores y teniendo en cuenta las componentes imaginarias se
comprueba fácilmente:
Im(Uɺ 1 (ωt ) + Uɺ 2 (ωt )) = Im(Uɺ 1 (ωt )) + Im(Uɺ 2 (ωt ))
Im( Iɺ (ωt ) − Iɺ (ωt )) = Im( Iɺ (ωt )) − Im( Iɺ (ωt ))
1
2
1
Ecs.(5)
2
Vale resultado equivalente para las partes reales pero se ha usado en todo este análisis la función seno como
base y es justamente la que corresponde a la componente imaginaria de los fasores.
De las Ecs.(5) surge que la suma o resta de dos señales senoidales de igual frecuencia y desfasaje cualquiera,
es igual a la parte imaginaria de la suma de los fasores cuyas partes imaginarias son las señales senoidales en
cuestión.
e) Dado un fasor Đ(ωt+ϕ) también es fácil comprobar:
d
d
(Im( Iɺ(ωt + ϕ )) = Im( Iɺ(ωt + ϕ ))
dt
dt
∫ Im(Iɺ(ωt + ϕ )) ⋅ dt = Im(∫ Iɺ(ωt + ϕ ) ⋅ dt
Ecs.(6)
También resulta válida la aclaración hecha en el punto d)
Las Ecs. (6) muestran que si se requiere calcular la derivada o la integral de una función senoidal es igual
calcular dichas operaciones sobre el correspondiente fasor y del resultado calcular la parte imaginaria.
Si se presta atención a las propiedades matemáticas casi obvias de los puntos c), d) y e) puede concluirse lo
siguiente:
Los fasores cuyas componentes imaginarias corresponden a corrientes o tensiones senoidales causas,
multiplicados ya sea por resistencias y/o reactancias, o conductancias y/o susceptancias respectivamente, se
transforman en fasores cuya componente imaginaria representa la tensión o corriente senoidales
consecuencias.
Es decir puede expresarse una ley de Ohm para alterna mucho más potente que la hecha en forma
trigonométrica.
No resulta difícil comprobar, usando las propiedades indicadas en c) y en e) la anterior afirmación.
I-. Caso de conductancia G con causa e = E sen(ωt)
e = E ⋅ sen(ωt ) = Im( Eɺ (ωt )) = Im( E ⋅ e jωt )
i = e ⋅ G = Im( Eɺ (ωt )) ⋅ G = Im( Eɺ (ωt ) ⋅ G ) = Im( Iɺ(ωt ))
Eɺ (ωt ) ⋅ G = Iɺ(ωt )
Eɺ (ωt ) / Iɺ(ωt ) = R
ó
Ing. Marcos Deorsola
Prof. Tit de Teoría de Circuitos I y de Electrotecnia y Electrónica
Departamento de Electrotecnia
Facultad de Ingeniería
Universidad Nacional de La Plata
Ing. Pablo Morcelle del Valle
Prof. Adj. de Electrotecnia y Electrónica
Departamento de Electrotecnia
Facultad de Ingeniería
Universidad Nacional de La Plata
Fasores_Rev2005
3
II-. Caso de una auto inducción L con causa i = I sen(ωt)
i = I ⋅ sen(ωt ) = Im( Iɺ(ωt )) = Im( I ⋅ e jωt )
d
d
d
u L = L ⋅ i = L ⋅ (Im( Iɺ(ωt )) = Im( L ⋅ I ⋅ e jωt ) = Im( j ⋅ ω ⋅ L ⋅ I ⋅ e jωt )
dt
dt
dt
= Im( j ⋅ X L ⋅ Iɺ(ωt )) = Im(Uɺ L (ωt ))
Uɺ L (ωt ) = j ⋅ X L ⋅ Iɺ(ωt )
ó
Uɺ L (ωt ) / Iɺ(ωt ) = j ⋅ X L = X L ⋅ e jπ / 2 = X L (π / 2)
III-. Caso de un capacitor C con causa i = I sen(ωt)
1
1
1
uC = ⋅ ∫ i ⋅ dt = ⋅ ∫ Im(Iɺ(ωt ) ⋅ dt = Im( ⋅ ∫ I ⋅ e jωt ⋅ dt ) =
C
= Im(
C
I
j ⋅ω ⋅C
⋅e
C
jωt
) = Im( − j ⋅ XC ⋅ Iɺ(ω t )) = Im(Uɺ (ωt ))
Uɺ C (ωt ) = − j ⋅ X C ⋅ Iɺ(ωt )
− jπ / 2
U C (ωt ) / I (ωt ) = − j ⋅ X C = X C ⋅ ⋅ e
= X C ( −π / 2)
ó
Las consideraciones del punto d) hacen válidas las leyes de Kircchoff con fasores, es decir pueden sumarse las
caídas de tensión en una malla o las corrientes en un nodo operando con fasores y determinando la parte
imaginaria al resultado.
ɺ
ɺ
Si bien de los resultados obtenidos con los operadores se requiere determinar la parte imaginaria, ésta etapa
puede obviarse por saberse que será una forma senoidal de la misma frecuencia que las causas y relaciones de
amplitud y fase indicadas en los mismos operadores.
Por último no es imprescindible trabajar con Uɺ (ωt ) ó Iɺ(ωt ) , sino con una imagen detenida en un instante t
cualquiera de estos fasores (los cuales rotan con una velocidad angular ). Es decir puede operarse con U ó
I que representan dicha imagen detenida.
Ing. Marcos Deorsola
Prof. Tit de Teoría de Circuitos I y de Electrotecnia y Electrónica
Departamento de Electrotecnia
Facultad de Ingeniería
Universidad Nacional de La Plata
Ing. Pablo Morcelle del Valle
Prof. Adj. de Electrotecnia y Electrónica
Departamento de Electrotecnia
Facultad de Ingeniería
Universidad Nacional de La Plata